Stability analysis of differential scheme for dynamic equations of mooring cable system

Shi, Ruizhi; Zhang, Suxia; Liu, Xijun; Cui, Fujiang; Zhou, Anqi

doi:10.21595/vp.2018.20282

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2018

Check for updates

Stability analysis of differential scheme for dynamic equations of mooring cable system

Ruizhi Shi¹

Suxia Zhang²

Xijun Liu³

Fujiang Cui⁴

Anqi Zhou⁵

^{1, 2, 3, 4, 5}Department of Mechanics, School of Mechanical Engineering, Tianjin University, Tianjin, 300354, P. R. China

^{1, 2, 3, 4, 5}Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control, Tianjin, 300354, P. R. China

Corresponding Author:

Suxia Zhang

Cite the article Download PDF

Downloads 1350

CrossRef Citations 1

Abstract

The mooring cable system in plane motion can be modeled as two coupled partial differential equations, which can be numerical solved by finite difference method directly. The difference scheme is analyzed, and parameters selection for time-marching of displacement and velocity are deduced. The stability condition of the scheme is analyzed through Fourier series method, and parameters range which match stable scheme is given. Then, the parameters range is verified by a numerical example.

1. Introduction

Cable structure is widely used in engineering because of its light weight and good flexibility, and mooring cable system is one of them. It is necessary to analyze the dynamic characteristics and tension of the cable to ensure engineering safety.

In order to accurately analyze the characteristics of cable structure, a large number of scholars have studied a lot of cable models and calculation methods. In the 1980s, Irvine [1] systematically summarized the previous studies on the static and dynamic state of different cable structures. It had ignored nonlinear factors in previous studies. Later, when considering the great influence of nonlinear factors on the system motion, scholars gradually take the nonlinear factors in the study of dynamic cable models. Perkins et al. [2-4] derived the three-dimensional dynamic equation of the fixed elastic cable through Hamilton principle, and studied the motion along the tangential, normal and auxiliary normal direction of the cable respectively; Then based on this model, the resonance response of elastic cable in steady flow is studied; Later, a theoretical model for the vibration of floating body with cable was established. According to this model, Zhang Suxia et al. [5, 6] studied the tension characteristic and impact tension under taut-slack condition. This model for characterize the spatial dynamical motion of elastic cables is still used today.

When solving the coupled system of partial differential equations, the decoupling solution can be obtained by Galerkin method; Meanwhile, it also can be solved directly by finite element or finite difference method [7], and the difference scheme used in the finite difference method must be stable. Therefore, in this paper, the stability analysis of the difference scheme used to solve the dynamic equations of the mooring cable system is carried out, which in order to obtain the condition of the absolute stability of the scheme, and parameters of the time- marching function are determined.

2. Model

Dynamic equations of mooring cable system in plane can be written as [2]:

1

\{\begin{array}{l} ρ A {\ddot{U}}_{1} = \frac{\partial}{\partial s} [(P + E A ε) (1 + \frac{\partial U_{1}}{\partial s} - κ U_{2})] - κ (P + E A ε) (\frac{\partial U_{2}}{\partial s} + κ U_{1}) \\ - (ρ - ρ_{w}) A g l_{t} + F_{1}, \\ ρ A {\ddot{U}}_{2} = \frac{\partial}{\partial s} [(P + E A ε) (\frac{\partial U_{2}}{\partial s} + κ U_{1})] + κ (P + E A ε) (1 + \frac{\partial U_{1}}{\partial s} - κ U_{2}) \\ - (ρ - ρ_{w}) A g l_{n} + F_{2}, \end{array}

where $U_{1}$ and $U_{2}$ represent tangential and normal displacement of the cable from static equilibrium respectively; $s$ is the arc length coordinate of the unstretched cable; $ρ$ is cable’s density, and $ρ_{w}$ is fluid's density; $A$ is the cross-sectional area; $P$ is the pretension; $E$ is the elastic modulus; $κ$ is the curvature of the cable from static equilibrium; $ε$ is the dynamic Lagrangian strain defined as Eq. (2); $g$ is the gravitational acceleration; $l_{t} = s i n θ$ and $l_{n} = c o s θ$ are direction cosines, and $θ$ is the angle between tangential direction of the cable equilibrium and horizontal direction based on absolute coordinates; $F_{1}$ and $F_{2}$ are tangential and normal restoring forces of the cable in motion, which can be approximated by Morrison formula as Eq. (3):

2

ε = \frac{\partial U_{1}}{\partial s} - κ U_{2} + \frac{1}{2} [{(\frac{\partial U_{1}}{\partial s} - κ U_{2})}^{2} + {(\frac{\partial U_{2}}{\partial s} + κ U_{1})}^{2}],

3

\{\begin{array}{l} F_{1} = C_{a t} ρ_{w} \frac{π d^{2}}{4} {\ddot{U}}_{1} + C_{d t} \frac{ρ_{w} d}{2} |{\dot{U}}_{1}| {\dot{U}}_{1}, \\ F_{2} = C_{a n} ρ_{w} \frac{π d^{2}}{4} {\ddot{U}}_{2} + C_{d n} \frac{ρ_{w} d}{2} |{\dot{U}}_{2}| {\dot{U}}_{2}, \end{array}

where $C_{a t}$ , $C_{d t}$ , $C_{a n}$ and $C_{d n}$ are tangential and normal drag coefficients; $d$ is the effective diameter of cable.

3. Numerical solution by finite difference method

The model is a problem of partial differential equations, which can be numerical solved by finite difference method.

3.1. Difference scheme and coefficient determination

The spatial differentiation can be obtained in reference [8]. Fourth-order formulas for first and second derivatives are expressed as Eq. (4), (5):

4

\frac{\partial u_{j}^{k}}{\partial s} = \frac{1}{24 Δ s} [\begin{matrix} - 50 & 96 & - 72 & 32 & - 6 \\ - 6 & - 20 & 36 & - 12 & 2 \\ 2 & - 16 & 0 & 16 & - 2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 2 & - 16 & 0 & 16 & - 2 \\ - 2 & 12 & - 36 & 20 & 6 \\ 6 & - 32 & 72 & - 96 & 50 \end{matrix}] [\begin{matrix} u_{j - 2}^{k} \\ u_{j - 1}^{k} \\ u_{j}^{k} \\ u_{j + 1}^{k} \\ u_{j + 2}^{k} \end{matrix}] + O (Δ s^{4}),

5

\frac{\partial^{2} u_{j}^{k}}{\partial s^{2}} = \frac{1}{24 Δ s^{2}} [\begin{matrix} 90 & - 308 & 428 & - 312 & 122 & - 20 \\ 20 & - 30 & - 8 & 28 & - 12 & 2 \\ - 2 & 32 & - 60 & 32 & - 2 \\ ⋱ & ⋱ & ⋱ & ⋱ & ⋱ & ⋱ \\ - 2 & 32 & - 60 & 32 & - 2 \\ 2 & - 12 & 28 & - 8 & - 30 & 20 \\ - 20 & 122 & - 312 & 428 & - 308 & 90 \end{matrix}] [\begin{matrix} u_{j - 2}^{k} \\ u_{j - 1}^{k} \\ u_{j}^{k} \\ u_{j + 1}^{k} \\ u_{j + 2}^{k} \end{matrix}] + O (Δ s^{4}),

where $k$ is the time coordinate and $j$ is the spatial coordinate.

A time-marching algorithm for solution of the nodal displacement $u_{j}^{k}$ and velocity $v_{j}^{k}$ is expressed in reference [9] as Eq. (6), (7):

6

u_{j}^{k + 1} = u_{j}^{k} + v_{j}^{k} Δ t + \frac{1}{2} β_{1} Δ t^{2} (a_{j}^{k} + β_{2} a_{j}^{k + 1}),

7

v_{j}^{k + 1} = v_{j}^{k} + \frac{1}{2} α_{1} Δ t (a_{j}^{k} + α_{2} a_{j}^{k + 1}) .

The nodal acceleration $a_{j}^{k + 1}$ at $k +$ 1 time point can be obtained by dynamic equations of the mooring cable system, while expressions on the right hand side of the equation are at k time point. $Δ t$ is the time step; $α_{1}$ , $α_{2}$ , $β_{1}$ and $β_{2}$ are weighting parameters, and the selection condition can be proposed by using the method of undetermined coefficients on second-order backwards differencing in time as Eq. (8):

8

\frac{\partial^{2} u^{k + 1}}{\partial t^{2}} = \frac{\frac{\partial u^{k + 1}}{\partial t} - \frac{\partial u^{k}}{\partial t}}{Δ t} + O (Δ t) = \frac{u^{k + 1} - u^{k}}{Δ t^{2}} - \frac{u^{k} - u^{k - 1}}{Δ t^{2}} + O (Δ t^{2}) .

Here is in the same spatial coordinate, so subscript can be omitted.

Substitute Eq. (6), (7) into Eq. (8) leads to Eq. (9):

9

\frac{\partial^{2} u^{k + 1}}{\partial t^{2}} = \frac{1}{2} β_{1} β_{2} a^{k + 1} + \frac{1}{2} (α_{1} α_{2} + β_{1} - β_{2}) a^{k} + \frac{1}{2} (α_{1} - β_{1}) a^{k - 1} + O (Δ t^{2}) .

Due to $\frac{\partial^{2} u^{k + 1}}{\partial t^{2}} = a^{k + 1}$ , there are three conditions for selecting $α_{1}$ , $α_{2}$ , $β_{1}$ and $β_{2}$ as Eq. (10):

10

\{\begin{array}{l} α_{1} = β_{1}, \\ β_{1} β_{2} = 2, \\ α_{1} α_{2} + β_{1} - β_{2} = 0 . \end{array}

3.2. Stability analysis of difference scheme

By using Fourier series method (Von Neumann method) [7], the stability condition for the above scheme is analyzed.

The magnitude of $Δ s$ is associated with the length of the mooring cable, therefore non-dimensional method is carried out for Eq. (1), let:

{\hat{u}}_{1} = \frac{U_{1}}{L}, {\hat{u}}_{2} = \frac{U_{2}}{L}, \hat{s} = \frac{s}{L}, \hat{t} = \frac{t}{1 s e c}, M = ρ A L, \hat{P} = \frac{P}{M L} \cdot 1 s e c^{2},

\hat{E} = \frac{E}{ρ L^{2}} \cdot 1 s e c^{2}, \hat{κ} = κ \cdot L, \hat{d} = \frac{d}{L}, {\hat{F}}_{1} = \frac{F_{1}}{M} \cdot 1 s e c^{2}, {\hat{F}}_{2} = \frac{F_{2}}{M} \cdot 1 s e c^{2},

{G_{t} = \frac{(ρ - ρ_{w}) A g l_{t}}{M} \cdot 1 s e c^{2}, G}_{n} = \frac{(ρ - ρ_{w}) A g l_{n}}{M} \cdot 1 s e c^{2},

where $L$ is the original length of the mooring cable; and $M$ is the cable’s mass. For Fourier series method is effective only in the linear system, so linearize the equations is necessary. Through the cable static equilibrium, a relation equation between the pretension and the gravity can be obtained; then simplified coefficients of restoring forces are substituted by $ξ$ :

\frac{\partial \hat{P}}{\partial \hat{s}} = G_{t}, \hat{P} \hat{κ} = G_{n}, {\hat{F}}_{1} = f ({\dot{\hat{u}}}_{1}^{2}) + ξ_{1} {\ddot{\hat{u}}}_{1}, {\hat{F}}_{2} = f ({\dot{\hat{u}}}_{2}^{2}) + ξ_{2} {\ddot{\hat{u}}}_{2},

{ξ_{1} = C_{a t} ρ_{w} \frac{π {\hat{d}}^{2}}{4}, ξ}_{2} = C_{a n} ρ_{w} \frac{π {\hat{d}}^{2}}{4} .

Finally, a non-dimensional linear difference scheme can be got:

11

\{\begin{array}{l} \begin{array}{l} (1 - ξ_{1}) {\ddot{\hat{u}}}_{1 j}^{k + 1} = (\hat{E} + \hat{P}) \frac{\partial^{2} {\hat{u}}_{1 j}^{k}}{\partial {\hat{s}}^{2}} + \frac{\partial \hat{P}}{\partial \hat{s}} \frac{\partial {\hat{u}}_{1 j}^{k}}{\partial \hat{s}} - {\hat{κ}}^{2} \hat{P} {\hat{u}}_{1 j}^{k} - (2 \hat{P} \hat{κ} + \hat{E} \hat{κ}) \frac{\partial {\hat{u}}_{2 j}^{k}}{\partial \hat{s}} \\ - (\hat{P} \frac{\partial \hat{κ}}{\partial \hat{s}} + \hat{E} \frac{\partial \hat{κ}}{\partial \hat{s}} - \hat{κ} \frac{\partial \hat{P}}{\partial \hat{s}}) {\hat{u}}_{2 j}^{k}, \end{array} \\ \begin{array}{l} (1 - ξ_{2}) {\ddot{\hat{u}}}_{2 j}^{k + 1} = \hat{P} \frac{\partial^{2} {\hat{u}}_{2 j}^{k}}{\partial {\hat{s}}^{2}} + \frac{\partial \hat{P}}{\partial \hat{s}} \frac{\partial {\hat{u}}_{2 j}^{k}}{\partial \hat{s}} - {\hat{κ}}^{2} (\hat{P} + \hat{E}) {\hat{u}}_{2 j}^{k} + (2 \hat{P} \hat{κ} + \hat{E} \hat{κ}) \frac{\partial {\hat{u}}_{1 j}^{k}}{\partial \hat{s}} \\ + (\hat{P} \frac{\partial \hat{κ}}{\partial \hat{s}} + \hat{κ} \frac{\partial \hat{P}}{\partial \hat{s}}) {\hat{u}}_{1 j}^{k} . \end{array} \end{array}

Substitute Eq. (4), (5) into Eq. (11), then the discrete Fourier Transform is used as Eq. (12):

12

{\hat{u}}^{k + 1} (ζ) = \frac{1}{\sqrt{2 π}} \sum_{j = - \infty}^{\infty} e^{- i j ζ} {\hat{u}}_{j}^{k + 1},

and derive out Eq. (13) to express $\hat{u}$ which increases with time changes:

13

[\begin{array}{l} {\hat{u}}_{1}^{k + 1} (ζ) \\ {\hat{u}}_{2}^{k + 1} (ζ) \end{array}] = G [\begin{array}{l} {\hat{u}}_{1}^{k} (ζ) \\ {\hat{u}}_{2}^{k} (ζ) \end{array}],

here, $G$ is a two dimensional growth matrix as:

G = [\begin{array}{l} a & b \\ c & d \end{array}],

where:

14

a = \frac{Δ t^{2}}{1 - ξ_{1}} \{\frac{\hat{E} + \hat{P}}{24 Δ {\hat{s}}^{2}} [- 8 {(c o s ζ - 4)}^{2} + 72] + \frac{\partial \hat{P}}{\partial \hat{s}} \frac{1}{24 Δ \hat{s}} [- 8 (c o s ζ - 4) s i n ζ] - {\hat{κ}}^{2} \hat{P}\},

15

b = \frac{Δ t^{2}}{1 - ξ_{1}} \{- \frac{2 \hat{P} \hat{κ} + \hat{E} \hat{κ}}{24 Δ \hat{s}} [- 8 (c o s ζ - 4) s i n ζ] - (\hat{P} \frac{\partial \hat{κ}}{\partial \hat{s}} + \hat{E} \frac{\partial \hat{κ}}{\partial \hat{s}} - \hat{κ} \frac{\partial \hat{P}}{\partial \hat{s}})\},

16

c = \frac{Δ t^{2}}{1 - ξ_{2}} \{\frac{2 \hat{P} \hat{κ} + \hat{E} \hat{κ}}{24 Δ \hat{s}} [- 8 (c o s ζ - 4) s i n ζ] + \hat{P} \frac{\partial \hat{κ}}{\partial \hat{s}} + \hat{κ} \frac{\partial \hat{P}}{\partial \hat{s}}\},

17

d = \frac{Δ t^{2}}{1 - ξ_{2}} \{\frac{\hat{P}}{24 Δ {\hat{s}}^{2}} [- 8 {(c o s ζ - 4)}^{2} + 72] + \frac{\partial \hat{P}}{\partial \hat{s}} \frac{1}{24 Δ \hat{s}} [- 8 (c o s ζ - 4) s i n ζ] - {\hat{κ}}^{2} (\hat{P} + \hat{E})\} .

The eigenvalue equation is $(λ - a) (λ - d) - b c =$ 0, also can be written as $λ^{2} - (a + d) λ + a d - b c =$ 0. For the difference scheme as Eq. (11) is absolutely stable, the eigenvalue must satisfy the following condition:

18

|λ| \leq 1 .

This inequality can be separated two sets, one is:

19

{(a - d)}^{2} + 4 b c < 0 \cap |a d - b c| \leq 1,

and the other one is:

20

{(a - d)}^{2} + 4 b c \geq 0 \cap a + d - a d + b c \leq 1 \cap a + d + a d - b c \geq - 1 .

The difference scheme as Eq. (11) will be absolutely stable, if $Δ \hat{t}$ and $Δ \hat{s}$ satisfy either of Eq. (19), (20).

4. Numerical example

According to reference [10], structure parameters and environmental parameters of the mooring cable are taken as Table 1. The cable motion belongs to forced vibration, and there supposes a sine displacement excitation on the upper point of the cable.

Substitute parameters into Eqs. (14)-(17) and make judgments about Eqs. (19), (20).

The results show that ${(a - d)}^{2} + 4 b c \geq$ 0 is always tenable, so $Δ \hat{t}$ and $Δ \hat{s}$ which match condition Eq. (19) are empty set. $Δ \hat{t}$ and $Δ \hat{s}$ which match condition Eq. (20) are shown in Fig. 1. Values range of $Δ \hat{t}$ and $Δ \hat{s}$ are from 0 to 1. $Δ \hat{s}$ labels horizontal axis of the figure, and $Δ \hat{t}$ marks the vertical axis. The difference scheme will be absolutely stable, if $Δ \hat{t}$ and $Δ \hat{s}$ are in the red area. The three black lines along the border of red area are condition Eq. (20) when the two sides are equal. If $Δ \hat{t}$ and $Δ \hat{s}$ are out of the red area, the result may be divergent.

Table 1Structure parameters and environmental parameters of the mooring cable

Parameter	Data	Parameter	Data
Original length $L$ (m)	1400	Fluid’s density $ρ_{w}$ (kg⋅m^-3)	1000
Effective diameter $d$ (m)	0.12	Tangential drag coefficients $C_{a t}$	1
Linear density $ρ A$ (kg⋅m^-1)	70.37	Tangential drag coefficients $C_{d t}$	0.05
Cross-sectional area $A$ (m²)	0.0113	Normal drag coefficients $C_{a n}$	1
Elastic modulus $E A$ (kN)	136064	Normal drag coefficients $C_{d n}$	1.2
Horizontal pretension at upper point $P_{0}$ (N)	8.5985×10⁵	Vertical pretension at upper point $V$ (N)	1.29574×10⁶

Fig. 1Δt^ and Δs^ which match condition Eq. (20)

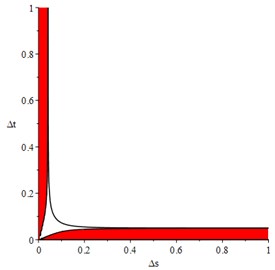
Extract two sets of data, respectively in and out of the red area, for numerical solution of dynamic equations of mooring cable system. The results are shown in Fig. 2.

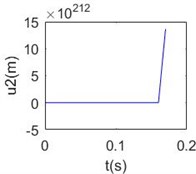
The time histories of tangential and normal displacement at 700 m point are shown in Fig. 2(a), (b). In these results, $Δ \hat{t} =$ 0.001 and $Δ \hat{s} =$ 1/280 are selected form the stable area, and we can get stable numerical solution. When $Δ \hat{t} =$ 0.01 and $Δ \hat{s} =$ 1/280, the results are divergent shown as Fig. 2(c), (d). That means the value selection must from the stable area, then convergent results can be got.

Furthermore, the numerical solution is more accurate if $Δ \hat{t}$ and $Δ \hat{s}$ are smaller. This difference scheme is absolutely stable only in linear system or some weak nonlinear system, so it’s better to solve nonlinear stability without linearization if nonlinear terms have strong effect of results.

Fig. 2Numerical solution of dynamic equations of mooring cable system at Δs^= 1/280: a) tangential displacement at 700 m point Δt^= 0.001, b) normal displacement at 700 m point Δt^= 0.001, c) tangential displacement at 700 m point Δt^= 0.01, d) normal displacement at 700 m point Δt^= 0.01

Numerical solution of dynamic equations of mooring cable system at Δs^= 1/280: a) tangential displacement at 700 m point Δt^= 0.001, b) normal displacement at 700 m point Δt^= 0.001, c) tangential displacement at 700 m point Δt^= 0.01, d) normal displacement at 700 m point Δt^= 0.01

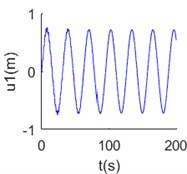
a)

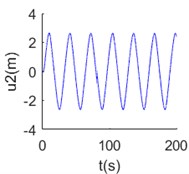
b)

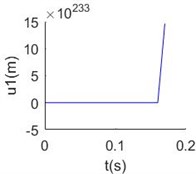
c)

d)

5. Conclusions

The mooring cable system in plane motion is modeled as two coupled partial differential equations, which can be numerical solved by finite difference method without decoupling. This numerical method needs the difference scheme is stable and parameters selection is reasonable. Through the calculation and analysis, conclusions are obtained as follow:

1) Three conditions of time-marching parameters are derived, which used for displacement and velocity in the same space point, and second order accuracy can be satisfied to describe acceleration under these conditions;

2) The stability of the dimensionless linear difference scheme is analyzed by using Fourier series method, and conditions of the stability are obtained. Through a numerical example, the results show that the difference scheme can be stable under the linear system, and accurate numerical solutions can be obtained. However, in the nonlinear system, the influence of nonlinear terms should be considered.

References

Irvine Max H. Cable Structures. The MIT Press, Cambridge, Massachusetts, London, England, 1981.

Search CrossRef
Perkins N. C., Mote C. D. Three-dimensional vibration of travelling elastic cables. Journal of Sound and Vibration, Vol. 114, Issue 2, 1987, p. 325-340.

Publisher
Kim W. J., Perkins N. C. Two-dimensional vortex-induced vibration of cable suspensions. Journal of Fluid and Structures, Vol. 16, Issue 2, 2002, p. 229-245.

Publisher
Kim W. J., Perkins N. C. Linear vibration characteristics of cable-buoy systems. Journal of Sound and Vibration, Vol. 252, Issue 3, 2002, p. 443-456.

Publisher
Tang Yougang, Zhang Suxia, Zhang Haiyan Study on snap tension induced by taut-slack in a mooring system. Journal of Vibration and Shock, Vol. 27, Issue 4, 2008, p. 70-72.

Search CrossRef
Zhang Suxia, Tang Yougang, Hou Shujun, Liu Xijun Characteristic analysis of stress wave in mooring line in taut-slack condition. Engineering Mechanics, Vol. 27, Issue 5, 2010, p. 53-59.

Search CrossRef
Zhang Wensheng Finite Difference Methods for Partial Differential Equations in Science Computation. Higher Education Press, Beijing, China, 2006.

Search CrossRef
Schiesser W. E. The Numerical Method of Lines Integration of Partial Differential Equations. Academic Press, San Diego, 1991.

Search CrossRef
Nejad Mohammad Behbahani Wave Propagation in Elastic Cables with and Without Fluid Interaction. Mechanic Engineering in the University of Michigan, 1997, p. 79.

Search CrossRef
Wang Xinggang Coupled Dynamic Analysis of Deepwater Floating Structure and the Mooring system. Shanghai Jiao Tong University Press, Shanghai, China, 2014, p. 36-37.

Search CrossRef

Cited by

Modeling and Numerical Simulation of Semitensioned Mooring Line under Taut-Slack State

Ruizhi Shi | Suxia Zhang | Xijun Liu | Chong Tian | Fehmi Najar

(2023)

About this article

Received

04 October 2018

Accepted

09 October 2018

Published

19 October 2018

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2018.20282

Keywords

mooring cable system

finite difference method

difference scheme

stability condition

Acknowledgements

The authors gratefully acknowledge the support of the National Natural Science Foundation of China (51479136), the Project of Tianjin Municipal Transportation Commission (2018B-33), the Project of Tianjin Natural Science Foundation (17JCYBJC18700).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2017 11 15

Prediction of dynamic characteristics of a pantograph-catenary system using the displacement compatibility

Guo Chen, Yiren Yang, Yang Yang

Research article

2017 09 30

Influence of catwalk design parameters on the galloping of constructing main cables in long-span suspension bridges

Pan Guo, Shengli Li, Chaoqun Wang, Yanan Hu, Dongwei Wang

Research article

2017 02 15

Dynamics simulation of microelectromechanical electrostatic actuator incorporating the squeeze-film damping effect

Chin-Chia Liu

Research article

2016 09 30

Investigation on chatter stability of thin-walled parts in high-speed milling based on relative transfer functions

Lida Zhu, Yang Ding, Changfu Liu, Zhiwei Xu

R. Shi, S. Zhang, X. Liu, F. Cui, and A. Zhou, “Stability analysis of differential scheme for dynamic equations of mooring cable system,” Vibroengineering PROCEDIA, Vol. 20, pp. 267–272, Oct. 2018, https://doi.org/10.21595/vp.2018.20282

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20282
UR  - https://doi.org/10.21595/vp.2018.20282
TI  - Stability analysis of differential scheme for dynamic equations of mooring cable system
T2  - Vibroengineering PROCEDIA
AU  - Zhang, Suxia
AU  - Shi, Ruizhi
AU  - Liu, Xijun
AU  - Cui, Fujiang
AU  - Zhou, Anqi
PY  - 2018
DA  - 2018/10/19
PB  - JVE International Ltd.
SP  - 267-272
VL  - 20
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhang_2018,
	doi = {10.21595/vp.2018.20282},
	url = {https://doi.org/10.21595/vp.2018.20282},
	year = 2018,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {20},
	pages = {267--272},
	author = {Suxia Zhang and Ruizhi Shi and Xijun Liu and Fujiang Cui and Anqi Zhou},
	title = {Stability analysis of differential scheme for dynamic equations of mooring cable system},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]S. Zhang, R. Shi, X. Liu, F. Cui, and A. Zhou, “Stability analysis of differential scheme for dynamic equations of mooring cable system,” Vibroengineering PROCEDIA, vol. 20, pp. 267–272, Oct. 2018, doi: 10.21595/vp.2018.20282.

Copy IEEE

Copied to clipboard!

Zhang, Suxia, Ruizhi Shi, Xijun Liu, Fujiang Cui, and Anqi Zhou. “Stability Analysis of Differential Scheme for Dynamic Equations of Mooring Cable System.” Vibroengineering PROCEDIA 20 (October 19, 2018): 267–72. https://doi.org/10.21595/vp.2018.20282.

Copy Chicago

Copied to clipboard!

Stability analysis of differential scheme for dynamic equations of mooring cable system

Abstract

1. Introduction

2. Model

3. Numerical solution by finite difference method

3.1. Difference scheme and coefficient determination

3.2. Stability analysis of difference scheme

4. Numerical example

5. Conclusions

References

Cited by

About this article

Related Articles