Dynamics simulation of microelectromechanical electrostatic actuator incorporating the squeeze-film damping effect

1. Introduction

Micro-electro-mechanical systems (MEMS) devices have applications in many engineering fields such as communications [1], automotive industry [2] and chemical [3], and so on. Such devices are generally actuated using either electrostatic [4], electromagnetic [5], thermal or piezoelectric [6] techniques. Of these various techniques, electrostatic actuation schemes are the most commonly employed due to their fast response, low power consumption, reliability and their batch fabrications [7]. Actually, in the electrostatic actuation of a micro-structure system, the electrostatic force is produced from the voltages of two electrodes. If the electrostatic force is greater than the elastic restoring force of the micro-structure system, this represents an unstable phenomenon, and the two electrodes attract and come into contact with each other suddenly [8]. The critical value of the voltage is defined as the pull-in voltage, which has a tremendous influence on the electrostatic device. For example, the electrostatic device is regarded as a digital actuator when the operation voltage is greater than the pull-in voltage and the upper electrode can be attracted to the fixed bottom electrode very quickly; therefore, the pull-in voltage limits the operation range of the actuator. The pull-in behavior phenomenon, however, can be used in the design of such components as switches and relays. Hence, the pull-in voltage is a very important parameter in the design of microelectromechanical devices.

Accordingly, many researchers have proposed more sophisticated techniques for modeling the nonlinear behavior of electrostatic actuators which including the micro-plate and the micro-beam. Chao et al. [9] proposed a novel computational method for predicting the static pull-in event between two micro-plates actuated by a distributed electrostatic force. Chen et al. [10] used a hybrid differential transformation / finite difference method to analyze the nonlinear dynamic behavior of a clamped-clamped micro-beam in the absence of a squeeze-film damping effect. Younis et al. [11] presented a continuous reduced-order model for predicting the static pull-in voltage and position of electrically actuated MEMS micro-beams. Taking into account geometric nonlinearity and residual stresses, Vogl and Nayfeh [12] presented an analytical continuous reduced-order model (macromodel) for an electrically actuated clamped circular plate with a uniform residual biaxial plane stress consideration for actuated, and than using a Galerkin approach method to discretize the microstructure.

To increase the actuation efficiency and detection sensitivity of MEMS-based devices, the separation distance between the two electrodes must be minimized and the overlapping area between them maximized. Under such conditions, a squeeze-film damping effect occurs between the two electrodes as the upper electrode deforms [13]. The Squeeze-film damping can be modeled using the Reynolds equation, which is derived from the Navier–Stokes equations and the continuity equation. The main assumption is that the gas in the gap can be treated as a continuum. The validity of this assumption depends on the so-called Knudsen number ($K_n$) which defined as the ratio of the mean free path of the air particals to the film thickness. Based on the Knudsen number, the air flows can be divided into four regimes: continuum flow when $Kn<$ 0.01, slip flow when 0.01 $<K_n<$ 0.1, transitional flow when 0.1 $<Kn<$ 10 and free molecular flow when $Kn>$ 10. Krylov and Maimon [14] have studied the transient dynamics of an electrically actuated micro-beam considering the electrostatic forces, squeeze-film damping, and rotational inertia of a mass carried by the micro-beam.

Dynamic analysis currently MEMS devices are being positively developed for various widely applications of industries. Younis [15] examined the dynamic behavior of micro-beams subject to combined DC / AC loading and derived analytical expressions for the micro-beam motion under primary resonance conditions. Chen et al. [10] demonstrated that the hybrid differential transformation and finite difference method provides a precise and computationally-efficient means of analyzing the nonlinear dynamic behavior of fixed-fixed micro-beams.

In the present study, the hybrid numerical scheme comprising the differential transformation method and the finite difference method is applied to analyze the dynamic behavior of the circular micro-plate / the clamped-clamped micro-beam actuated by pure DC or combined DC / AC loading schemes. The analyses take account of the electrostatic coupling effect, the fringing field effect, the residual stress, the nonlinear electrostatic force, the axial stress effect and squeeze-film damping effect.

2. Differential transformation theory

Differential transformation theory was originally proposed by Zhou [16] in 1986 as a means of solving linear and nonlinear initial value problems in the circuit analysis field. However, later researchers extended its use to the analysis of the mechanical engineering domain [10, 13, 17]. The basic principles of the differential transformation method are introduced below. If $y\left(t\right)$ is an analyzable function in time domain $T$, a definition of the differential transformation of $x$ at $t=t_0$ in the $K$ domain is:

where $k$ belongs to the set of non-negative integers denoted as the $K$ domain, $Y(k;t_0)$ is the transformed function in the transformation domain, otherwise called the spectrum of $x\left(t\right)$ at $t=t_0$ in the $K$ domain, $M\left(k\right)$ is the weighting factor, and $q\left(t\right)$ is regarded as a kernel corresponding to $y\left(t\right)$. Both $M\left(k\right)$ and $q\left(t\right)$ are non-zero and $q\left(t\right)$ is an analyzable function in time domain $T$. Therefore, the differential inverse transformation of $Y(k;t_0)$ can be described as:

If $M\left(k\right)=H^k/k!$ and $q\left(t\right)=\text{1}$, where $H$ is the time interval. Let $t_0=\text{0}$; Eq. (1) then becomes:

The differential inverse transformation of $Y\left(k\right)$can then be expressed as below by Eq. (2):

Substituting Eq. (3) into Eq. (4) gives:

Eq. (5) can be derived by Taylor series expansion. Therefore, the main basic operation properties of the differential transform are listed below:

a) Linearity operation:

where $T$ denotes the differential transform and $\alpha$ and $\beta$ can be any real number.

b) Differential operation:

where $T$ denotes the differential transform and n is the order of differentiation [10, 13, 17].

3. Modeling of microelectromechanical electrostatic actuators

3.1. Modeling of clamped-clamped micro-beam

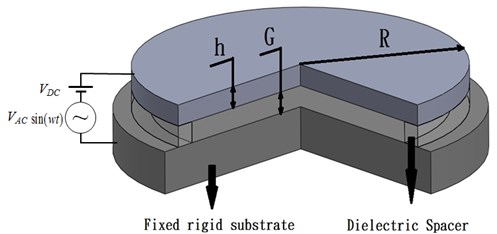
The analysis performed in this study considers the clamped-clamped micro-beam shown in Fig. 1. As shown, the upper plate is actuated by a driving voltage $V\left(t\right)=V_{DC}+V_{AC}\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$, where $V_{DC}$ is the DC polarization voltage, $V_{AC}$ is the magnitude of AC voltage, and $\omega$ is the excitation frequency. In deriving the governing equation of the clamped-clamped micro-beam which considers the fringing field effect, the residual stress and the squeeze-film damping effect within the beam. The corresponding governing equation is therefore given by [13]:

8

$\tilde{E}I\frac{{\partial }^{4}w}{\partial x^4}+\rho A\frac{{\partial }^{2}w}{\partial t^2}-\left[N_0+\frac{\tilde{E}A}{2L}{{\int }_0^L\left(\frac{\partial w}{\partial x}\right)}^{2}dx\right]\frac{{\partial }^{2}w}{\partial x^2}=F_E-F_S.$

Regarding the right-hand side of Eq. (1), $F_E$ represents the excitation force per unit beam length and is given by:

9

$F_E=\frac{{\epsilon }_{0}bV(t{)}^2}{2(G-w{)}^2}\left(1+0.65\frac{G-w}{b}\right),$

where ${\epsilon }_0$, $b$ and $G$ denote the permittivity of free space, the width of the micro-beam and the initial gap size between the upper and lower electrodes, respectively. Moreover, $\tilde{E}$ is the effective beam material modulus. For the case of a wide micro-beam (i.e., $b\ge 5h$), $\tilde{E}$ is equal to the plate modulus, i.e. $E/(1-{\nu }^2)$, where $\nu$ is the Poisson ratio and $h$ is the beam thickness. Conversely, for a narrow beam, $\tilde{E}$ is equal to the Young’s modulus, $E$. In Eq. (8), $I$ denotes the moment of inertia of the micro-beam, $N_0$ is a constant denoting the residual force acting on the beam and $w$ is the transverse displacement of the beam and varies as a function of both the longitudinal position $x$ and the time $t$, i.e.,$w=w(x,t)$. Note that the residual force is given by $N_0=\tilde{\sigma }bh$, where $\tilde{\sigma }$ is the residual stress and has the form of $\tilde{\sigma }=\sigma (1-\nu )$, in which $\sigma$ is the biaxial residual stress.

Finally, $F_S$ denotes the force acting on the beam due to the squeeze-film damping effect and is given by:

10

$F_S={\int }_0^b(P-P_a)dy,$

where $P$ is the absolute pressure in the air gap and $P_a$ is the ambient pressure. The net pressure can be expressed as $\stackrel{-}{P}=P-P_a$. The squeeze-film damping effect in Fig. 1 can be described by the nonlinear Reynolds equation:

11

$\frac{\partial }{\partial x}\left({\rho }_a{h_a}^3\frac{\partial P}{\partial x}\right)+\frac{\partial }{\partial y}\left({\rho }_a{h_a}^3\frac{\partial P}{\partial y}\right)=12\mu \frac{\partial \left({\rho }_a{h}_a\right)}{\partial t}.$

Note that$h_a\text{,}$${\rho }_a$ and $\mu$ represent the variable distance between the two electrodes ($h_a=G-w$), the density of the air in the air gap, and the effective viscosity of the air in the air gap, respectively.

Fig. 1Schematic illustration of the clamped-clamped micro-beam

3.2. Modeling of circular micro-plate

In deriving the governing equation of motion for the circular micro-plate shown in Fig. 2, the study considers both the residual stress within the plate and the squeeze-film damping effect between the two plates. The governing equation is therefore given as [8]:

12

$\rho h\frac{{\partial }^{2}w}{\partial t^2}+D\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}\right)\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right)-T_r\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right)=\frac{{\epsilon }_{0}V(t{)}^2}{2(G-w{)}^2}-P_n,$

where ${\epsilon }_0$, $h$ and $G$ are represented the permittivity of free space, the thickness of the circular micro-plate, and the initial gap height between the upper and lower plates, respectively. In addition, $V\left(t\right)$ is the voltage between the two plates, (i.e., $V\left(t\right)=V_{DC}+V_{AC}\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$), $\rho$ is the density of the micro circular plate, and $w$ is the transverse deflection of the circular micro-plate at a distance $r$ from the center of the plate. In other words, the symmetry transverse deflection of micro circular plate is irrelevant to polar coordinate $\theta$. Finally, $T_r$ is the residual stress within the plate, $P_n$ is the net pressure within the air gap and $D$ is the flexural rigidity of the plate, i.e.:

13

$D=E{h}^3/12(1-{\nu }^2),$

where $\nu$ and $E$ are the Poisson ratio and Young’s modulus of the upper circular plate, respectively. The squeeze-film damping effect within the air gap is modeled using the linearized compressible gas-film Reynolds equation [13], which has the form:

14

$\frac{{\partial }^2{P}_n}{\partial r^2}+\frac{1}{r}\frac{\partial P_n}{\partial r}=\frac{12\mu }{P_a{G}^3}\left(G\frac{\partial P_n}{\partial t}+P_a\frac{\partial h_a}{\partial t}\right),$

where $h_a$ and $\mu$ represent the variable distance between the two electrodes (i.e., $h_a=G-w$) and the effective viscosity of the air in the air gap, respectively. The net pressure in the air gap can be expressed as $P_n=P-P_a$, where $P$ is the absolute pressure in the gap and $P_a$ is the ambient pressure.

Fig. 2Schematic illustration of the circular micro-plate

4. Numerical results and discussion

4.1. Clamped-clamped micro-beam

In this section, the validity of the proposed hybrid numerical scheme was demonstrated by comparing the predicted value of the pull-in voltage with that obtained using different scheme in the literature and the computations were performed using MATLAB. Note that in performing the analysis, the material and geometry properties of the micro-beam were assigned the values given in Table 1. In performing the comparison, as shown in Table 2, it is seen that the pull-in voltage calculated using the proposed method is just 1.4 % lower than that presented in the literature.

Table 1Material and geometry parameters of the clamped-clamped micro-beam

Parameters / Symbol / Unit	Value
Young's modulus ($E$) (GPa)	151
Poisson’s Ratio ($\nu$)	0.3
Density ($\rho$) (kg/m3)	2332
Thickness of circular plate ($h$) (μm)	1.5
Initial gap ($G$) (μm)	1.18
Length of beam ($L$) (μm)	210
Biaxial residual stress ($\sigma$) (MPa)	6

Table 2Comparison of present analytical results and literature results for pull-in voltages

	Analytical results		Deviation
	Hybrid numerical scheme	DQM [18]	$e$ (%)
Pull-in Voltage (V)	27.7	28.1	1.4

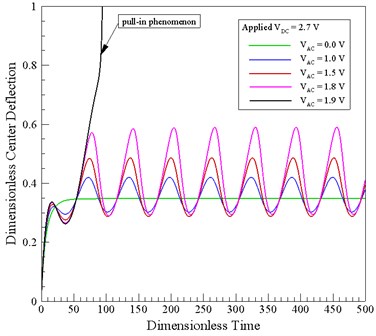
Fig. 3 shows the variation over time of the center-point deflection of the micro-beam for a constant DC voltage of 27 V and AC voltages in the range of 0-1.9 V. It is seen that the center-point deflection increases nonlinearly with an increasing AC voltage due to the nonlinear of the electrostatic coupling effect. Furthermore, it is observed that for a dimensionless time of less than 60, the DC voltage is unstable with a smaller deflection of the center point. In addition, the results show that for an AC voltage of 1.8 V, the micro-beam oscillates in a stable manner about the equilibrium deflection point. However, when the AC voltage is increased to 1.9 V, the micro-beam collapses and makes transient contact with the lower electrode.

Fig. 3Variation of dimensionless center-point displacement over time for different AC voltages

4.2. Circular micro-plate

Fig. 4 illustrates the variation of the center-point deflection of the micro-plate over time as a function of the AC voltage. Note that in performing the analysis, the basic material and geometry properties of the micro-plate is assigned in accordance with the data presented in Table 3. The results show that as the AC voltage increases, the center-point deflection of the micro-plate also increases as a result of the enhanced electrostatic coupling effect. In addition, it can be observed that the center deflection of the micro-plate increased nonlinearly as the AC voltage increased due to the micro-plate coupling effect.

Fig. 4Variation of dimensionless center-point displacement over time for constant DC voltage and AC voltages ranging from 0.0-11.5 V

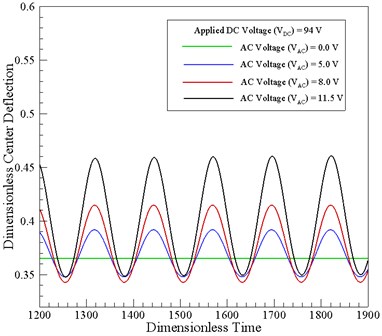
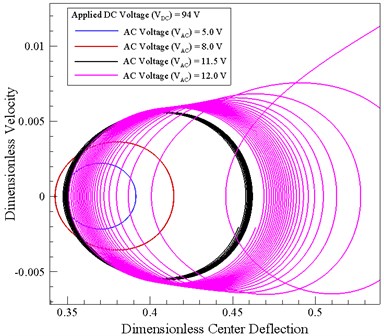
Fig. 5 shows the phase portraits of the circular micro-plate for a constant DC voltage of 94 V and AC voltages of 5.0 V, 8.0 V,11.5 V and 12.0 V, respectively. The results show that for an AC voltage less than 12.0 V, the system exhibits a stable behavior, i.e., the size of the orbit remains approximately constant over time. However, for an actuating voltage of 12.0 V, the size of the orbit gradually increases until the system becomes unstable and the pull-in event occurs.

Table 3Material and geometry parameters of the circular micro-plate

Parameters / Symbol / Unit	Value
Young’s modulus ($E$) (GPa)	130
Poisson’s Ratio ($\nu$)	0.23
Density ($\rho$) (kg/m3)	2330
Thickness of circular plate ($h$) (μm)	1.0
Initial gap ($G$) (μm)	1.0
Radius ($R$) (μm)	45

Fig. 5Phase portraits for the circular micro-plate given constant DC voltage of 94 V

5. Conclusions

The present study has analyzed the nonlinear dynamic behavior of the microelectromechanical electrostatic actuators subject to a squeeze-film damping effect by using a hybrid numerical scheme comprising the differential transformation method and the finite difference method. The validity of the proposed scheme has been confirmed by comparing the predicted value of the pull-in voltage for the micro-beam with the results presented in the literature. Finally, it has been shown that the stability of the circular micro-plate reduces as the magnitude of the AC voltage increases. Overall, the numerical results presented in this study show that the hybrid numerical scheme provides an accurate and computationally-efficient means of analyzing the nonlinear dynamic behavior of the microelectromechanical electrostatic actuators used in many of today’s MEMS-based systems.