Inferring causality from highly noisy uni-directionally coupled chaotic oscillators with small frequency mismatch

1. Introduction

Quantification of the causal effects between simultaneously observed systems from the analysis of time series recordings is essential in many scientific fields, including economics, climatology, ecosystems, electrical activity of the brain, or cardiorespiratory relations. Estimating the interdependence between the observed variables provides valuable knowledge regarding the processes that generate time series [1]. The Granger causality method [2] is the most well-known and principal method for identifying directional interactions between variables from their time series, and many modifications and extensions of the Granger causality test has been developed. The Granger test focuses on determining whether one time series is useful in forecasting another. If useful, the first system causally affects the second system. The conventional Granger causality test is based on autoregressive models and is particularly useful in stochastic linearly interconnected systems [3]. However, the appropriateness of direct application to nonlinear systems depends on the specific problem to be analyzed [4-6]. Therefore, new approaches have been proposed, including nonlinear extensions of Granger causality [4], transfer entropy [7], conditional mutual information [8], evolution map approach (EMA) [9, 10], convergent cross-mapping (CCM) method [5, 11, 12], and measures evaluating distances of conditioned neighbours in reconstructed state spaces [13-17], to name a few. A comprehensive review can be found in Focus Issue [18]. Specifically, CCM involves evaluating distances between conditioned neighbours in reconstructed state spaces and tests for causation between the driver (“master”) system $X$ and the driven (“slave”) system $Y$, by measuring the extent to which the historical states of reconstructed state space, $M_Y$ can reliably estimate states of reconstructed state space, $M_X$. To infer the direction of coupling, the opposite direction must also be assessed. Then, the direction of coupling is inferred based on asymmetries emerging from the calculations of the two possible causal directions. Most of the existing tools for detecting causality can make determinations of directionality in idealized conditions of sufficiently long, noise-free time series, but those determinations are relatively fragile in the presence of noise. However, the real-world datasets possess observational and process noise and may lack sufficient data. Taking the Rössler system as an example, it is shown in [19] that in the case of a small mismatch between the mutually incommensurate frequencies of the oscillators, changes in the phase dynamics of the slave oscillator are highly correlated with the dynamics of the phase difference between the oscillators. On the contrary, the phase dynamics of the master oscillator are not disturbed and do not correlate with the dynamics of the phase difference between the oscillators. This principle of asymmetries in correlations allows for efficiently assessing the presence and direction of coupling, especially in the case of weak coupling.

In this paper, we show that this method for estimating the causal effect in uni-directionally coupled chaotic oscillators can be successfully applied to a time series in high-noise environments due to its robustness against distortions caused by the noise reduction algorithms.

2. Description of the algorithm

We first give a brief introduction of the method [19] for assessing causality in uni-directionally coupled chaotic oscillators with small frequency mismatch. The approach is based on the correlation between changes in the phase dynamics of the slave oscillator and the dynamics of the phase difference between the oscillators. The instantaneous phase $\varphi \left(t\right)$ of a signal $s\left(t\right)$ is estimated using the Hilbert transform $H_t\left\{\bullet \right\}$:

where the analytic signal $z\left(t\right)$ can be understood as an embedding of the one-dimensional time-series in the two-dimensional complex plane and the function $H_t\left\{s\left(t\right)\right\}$ is the Hilbert transform of $s\left(t\right)$:

and P.V. means that the integral is taken in the sense of the Cauchy principal value. In the case that $z\left(t\right)$ evolves around a central region, the cyclic phase is computed by the following expression:

and $∆\varphi \left(t\right)={\varphi }_1\left(t\right)-{\varphi }_2\left(t\right)$ is the instantaneous phase difference between the corresponding signals $s_1\left(t\right)$ and $s_2\left(t\right)$ at time $t$. Furthermore, the phase difference is determined by $\mathrm{a}\mathrm{b}\mathrm{s}\left(modulo\pi \right)$, to specify the closeness of the phases between two oscillators without indicating the direction of the difference. As a result, the instantaneous phase difference oscillates between 0 and $\pi$ at a low instantaneous frequency defined as the time rate of change of $\mathrm{\Delta }\varphi \left(t\right)$ and determined by the difference in natural frequencies of the signals and by the coupling strength (more details in [20, 21]). In order to obtain the continuous dynamics of the phases ${\varphi }_1\left(t\right)$ and ${\varphi }_2\left(t\right)$, the phases are unwrapped by tracing the ≈2$\pi$ jumps in the time course of ${\varphi }_1\left(t\right)$ and ${\varphi }_2\left(t\right)$:

where ${\widehat{\varphi }}_i={\varphi }_i+\pi$; $i=$ 1, 2; $t_m$ are time points at which ${\widehat{\varphi }}_i$ reaches its maximum, i.e., ${\widehat{\varphi }}_i\approx \text{2}\pi$, $k=$ 1, …, $N$. For practical use, there is a convenient Matlab function unwrap. The unwrapped phases are detrended to detect subtle changes in their dynamics. Furthermore, the high-frequency small-amplitude irregular fluctuations of the ${\widehat{\varphi }}_i\left(t\right)$ and $\mathrm{\Delta }\varphi \left(t\right)$ are neglected, and only the oscillations at a low averaged frequency (${\mathrm{\Omega }}_D=〈d\mathrm{\Delta }\varphi \left(t\right)/dt〉$ for the instantaneous phase difference and ${\mathrm{\Omega }}_i=〈d{\widehat{\varphi }}_i/dt〉$ for the detrended ${\widehat{\varphi }}_i\left(t\right)$) are considered. The method is grounded on the fact that the unwrapped and detrended phase $\widehat{\varphi }\left(t\right)$ of the slave oscillator exhibits significant low-frequency oscillations synchronously with $\mathrm{\Delta }\varphi \left(t\right)$, i.e., is modulated according to the distance between phases and changes significantly with transition from in-phase to anti-phase state between coupled oscillators already at a weak coupling strength. On the contrary, no changes are observed in the unwrapped and detrended phase $\widehat{\varphi }\left(t\right)$ of the master oscillator synchronously with the phase difference. Therefore, the direction of coupling is inferred based on the asymmetries emerging from the correlations between $\mathrm{\Delta }\varphi \left(t\right)$ and $\widehat{\varphi }\left(t\right)$ for the slave oscillator and for the master oscillator. It is worth emphasizing that a high value of the correlation coefficient between $\mathrm{\Delta }\varphi \left(t\right)$ and $\widehat{\varphi }\left(t\right)$ for system $Y$ compared to the value of the correlation coefficient between $\mathrm{\Delta }\varphi \left(t\right)$ and $\widehat{\varphi }\left(t\right)$ for system $X$ indicates that system $X$ drives system $Y$. This runs in accordance with Granger’s method and counter to the CCM method. To recover the phase of the oscillating time series under high noise levels, we propose a nonlinear adaptive algorithm to recover continuous-time chaotic signals in heavy noise environments, based on a least-squares fit of the sum of sines and cosines, each with a time-varying phase to the state vectors of the neighbourhood of the reconstructed phase space. Let $X={\left\{x_t\right\}}_{t=1}^L$ and $Y={\left\{y_t\right\}}_{t=1}^L$ be two time series of finite length $L\in N$ contaminated by additive white Gaussian noise with zero mean and signal-to-noise ratio (SNR) of 0-5 dB. As a first step, $D$-dimensional attractor manifolds ${\mathbf{M}}_X$ and ${\mathbf{M}}_Y$ are reconstructed from lags of observable $X$ and $Y$ so that the state of the system in time $t$ is ${\mathbf{x}}_t={\left[x_t,x_{t+\tau },x_{t+2\tau },\cdots ,x_{t+\left(D-1\right)\tau }\right]}^T$ and ${\mathbf{y}}_t={\left[y_t,y_{t+\tau },y_{t+2\tau },\cdots ,y_{t+\left(D-1\right)\tau }\right]}^T$ respectively for $t=1$ to $t=L-\left(D-1\right)$, i.e., ${\mathbf{M}}_X={\left\{{\mathbf{x}}_t\right\}}_{t=1}^{L-\left(D-1\right)\tau }$ and ${\mathbf{M}}_Y={\left\{{\mathbf{y}}_t\right\}}_{t=1}^{L-\left(D-1\right)\tau }$, where $\tau$ is the time delay, and ${\left(\bullet \right)}^T$ denotes the transpose of a real matrix. One unit time delay and an embedding dimension approximately equal to one and a half of the fundamental period $\tilde{T}$ of the oscillations are used. The over-embedding technique contributes to the determination of valid neighbours at strong noise and to obtain a tradeoff between noise suppression and a distortion of the local chaotic dynamics. Further, the vector time series ${\mathbf{x}}_t$ and ${\mathbf{y}}_t$ are subjected to an identical preprocessing procedure as shown for vector time series ${\mathbf{x}}_t$. For every $i$, $i=\text{1},W,\text{2}W,\cdots ,L-\left(D-1\right)\tau$, $W=D/\text{2}$, point ${\mathbf{x}}_t$ in the reconstructed $D$-dimensional phase space, $r$, temporarily uncorrelated nearest neighbour points ${\left\{{\mathbf{x}}_i^j\right\}}_{j=1}^r$ are determined and mean value ${\widehat{x}}_i\left(t_k\right)$, $t_k=\text{1},\cdots ,D$, for this cloud of nearest neighbour points is calculated. We write:

as an approximation to ${\widehat{x}}_i\left(t_k\right)$, where $\omega =\text{2}\pi /\tilde{T}$ is the fundamental frequency of the sinusoids, ${\varphi }_q\left(t_k\right)=b\left(q-1\right)t_k$, and ${\beta }_{11q}$, ${\beta }_{21q}$, ${\beta }_{12q}$, ${\beta }_{22q}$, and ${\beta }_0$ are parameters to be estimated. The parameters $Q$ and $b$ are chosen experimentally. The vector parameter $\mathbf{\beta }$ is estimated using the known least-squares method:

where:

and ${\mathbf{M}}_{s+}$, ${\mathbf{M}}_{c+}$ are submatrices of size $D$×$Q$ encompassing $Q$ sines and $Q$ cosines respectively with a linear growth of the instantaneous frequency, ${\mathbf{M}}_{s-}$, ${\mathbf{M}}_{c-}$ are submatrices of size $D$×$Q$ encompassing $Q$ sines and $Q$ cosines respectively with a linear decrease of the instantaneous frequency, ${\mathbf{M}}_I$ is column vector $D$×1 of ones, and ${\left(\bullet \right)}^{†}$ denotes the Moore-Penrose pseudo-inverse of a given matrix. Knowing parameter $\mathbf{\beta }$, we can rewrite Eq. (5) as:

Estimated segments ${\tilde{x}}_i\left(t_k\right)$ overlap by $W$ points. To ensure that the fitting is continuous everywhere and to eliminate the jumps or discontinuities around the boundaries of neighbouring segments, we used the fitting for the overlapped region as described in [22]. Denote the fitted curve for the $i$th and ($i+1$)th segments by ${\tilde{x}}_i\left(t_k\right)$ and ${\tilde{x}}_{i+1}\left(t_k\right)$, respectively. Then the fitting for the overlapped region can be defined as:

where $w_1=\text{1}-\left(t_l-\text{1}\right)/W$, and $w_2=\left(t_l-\text{1}\right)/W$. As follows from Eq. (9), the weights decrease linearly with the distance between the point and the center of the segment. Such a weighting ensures symmetry and effectively eliminates any jumps or discontinuities around the boundaries of neighbouring segments. Numerical experiments on the Rössler system show that the proposed algorithm provides about 13 dB, on average, improvement in SNRs at initial SNR = 0 dB. The efficacy of this preprocessing algorithm enables to properly recover the phase of the noisy chaotic oscillator and, in consequence ensures the effectiveness of the proposed algorithm for inferring causality from highly noisy uni-directionally coupled chaotic oscillators.

3. Simulation results

To demonstrate the performance of the method we considered two examples of uni-directionally connected chaotic Rössler systems [12] with small frequency mismatch and having variable coupling strengths. The oscillators were coupled via a one-way driving relationship between variable $x_1$ of the driving system and variable $y_1$ of the responsive system:

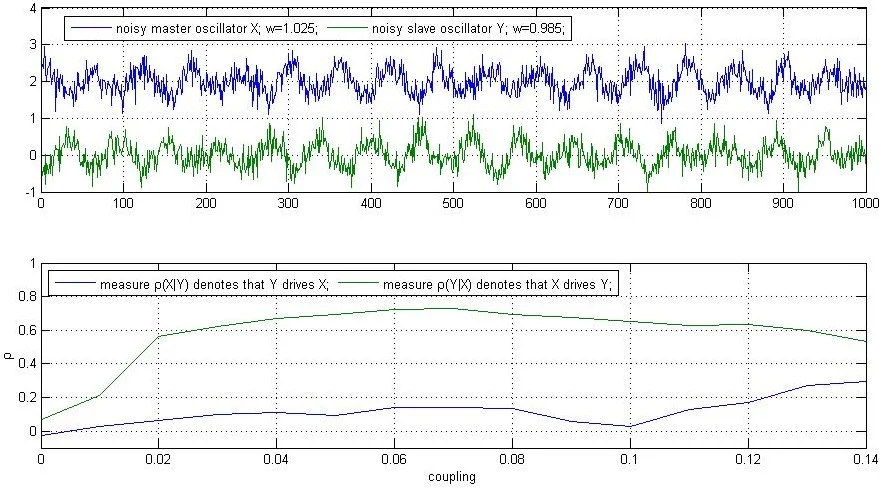
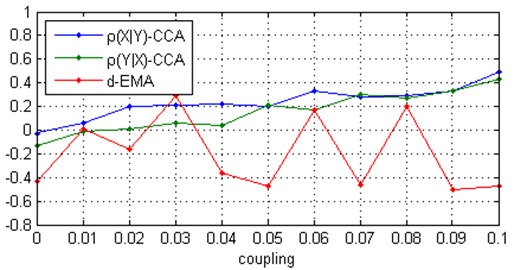
where ${\omega }_1\left(\text{1}\right)=$ 1.015, ${\omega }_2\left(\text{1}\right)=$ 0.985, ${\omega }_1\left(\text{2}\right)=$ 0.980, and ${\omega }_2\left(\text{2}\right)=$ 1.020. The coupling strength c was chosen from 0 to 0.14 with the step 0.01 for the first case and from 0 to 0.045 with the step 0.005 for the second case. The data were generated by Runge-Kutta integration with a step size of 0.1. The first 2000 data points were discarded. The total number of obtained data was 14000, and this resulted in around 60 samples per one average orbit around the attractor. Approximation parameters $Q$ and $b$ were chosen as $Q=$ 10, $b=$ 0.0012, i.e., the total number of sinusoids and cosines were 40, and the maximum deviation of the fundamental frequency amounted to approximately 11 %. The performance of the algorithm was evaluated by means of a 30-trial Monte Carlo simulation whereby the signals are contaminated by various realizations of additive zero-mean white Gaussian noise at a SNR = 0 dB. All data processing and analyses were performed using Matlab software (MathWorks, Natick, MA). Consequently, we denoted the direction from system $X$ to system $Y$ as$Y|X$ and the direction from $Y$ to $X$ as $X|Y$. Taking, for example, the measure $\rho$ (correlation coefficient): if $X$ drives $Y$, the measure $\rho \left(Y|X\right)$ is expected to be higher than $\rho \left(X|Y\right)$. As we can see from Fig. 1 and Fig. 2, the measure $\rho$ shows that system $X$ drives system $Y$ until the onset of synchronization, i.e., when their phases are locked, and when this method becomes meaningless. The mean gap between the measures $\rho \left(Y|X\right)$ and $\rho \left(X|Y\right)$ for noise-free signals and for signals contaminated with white Gaussian noise becomes roughly the same. For comparison two state-of-art algorithms were chosen: CCM and EMA. In the latter case, the directionality index $d$ was calculated using the Matlab code freely available on Ref. [23]. As we can see from Fig. 3, both methods fails to detect the causality at the conditions under study. CCM method shows false, i.e., weak opposite or bidirectional coupling direction, and the directionality index $d$ randomly oscillates between coupling directions. It is worth noting that the sign of correlation coefficient $\rho$ between $\mathrm{\Delta }\varphi \left(t\right)$ and $\widehat{\varphi }\left(t\right)$ for the responsive system can be positive or negative. In our example, $\rho$ is positive when the frequency of the driving system is higher than the frequency of the responsive system and negative when the frequency of the driving system is lower than the frequency of the responsive system.

Fig. 1Correlation coefficient ρ between Δϕt and ϕ^t computed for two uni-directionally coupled Rössler oscillators with natural frequencies ω1= 1.015, ω2= 0.985: a) for noise-free signals, b) the mean values and standard deviations (with error bars) from 30 independent Monte Carlo trials consisting of the noise-added signal at a SNR = 0 dB

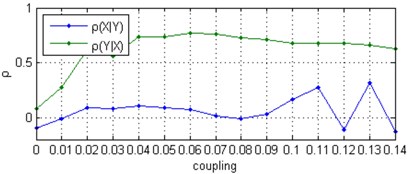
a)

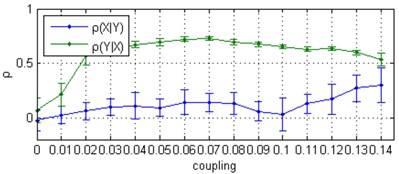
b)

Fig. 2Correlation coefficient ρ between Δϕt and ϕ^t computed for two uni-directionally coupled Rössler oscillators with natural frequencies ω1= 0.980, ω2= 1.020: a) for noise-free signals, b) the mean values and standard deviations (with error bars) from 30 independent Monte Carlo trials consisting of the noise-added signal at a SNR = 0 dB

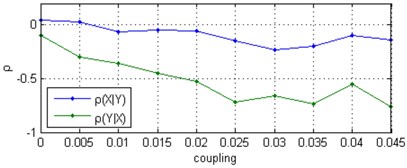
a)

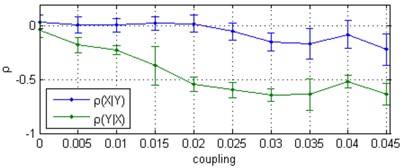
b)

Fig. 3Measures ρ obtained by CCM method and directionality index d obtained by EMA method for two uni-directionally coupled Rössler oscillators with natural frequencies ω1= 1.015, ω2= 0.985 and contaminated with noise at SNR = 0 dB

4. Conclusions

A simulation involving examples of uni-directionally connected chaotic Rössler-type systems shows that the algorithm for assessing causality in uni-directionally coupled chaotic oscillators based on the correlation between changes in the phase dynamics of the slave oscillator and the dynamics of the phase difference between the oscillators in combination with the proposed nonlinear adaptive denoising algorithm is an effective method to reveal the presence and the direction of coupling in uni-directionally coupled chaotic oscillators with a small frequency mismatch and embedded in heavy white Gaussian noise. The success of this approach is due to the robustness of the phase-based algorithm for assessing causality against unavoidable distortions of the local chaotic dynamics during the denoising process, and the comparison with the state-of-the-art methods shows that the proposed method is superior to the other approaches. Although in this work we explored a classical example of coupled chaotic Rössler oscillators frequently used for studying phase synchronization and causation, we believe that similar results can be obtained in other systems and future work should confirm this.