Abstract
The paper presents research done by means of numerical simulation on a rigid structure isolated with friction pendulums. To this aim, we design friction pendulums which differ by the shape and dimension of the cylindrical sliding surface, respectively by the friction coefficients. Our target was to find out how the structure responds to a given excitation when the structure is equipped with diverse friction pendulums. A sinusoidal excitation with the frequency of 1 Hz is applied and the response in terms of displacements is captured. We found that the frequency of the structure does not change with the FP radius but the amplitude of the displacement is strongly dependent on this parameter. Because the circular and elliptical sections of the FP provide the structure with different natural frequencies, the resonance is achieved at other radii.
1. Introduction
Base isolation for the protection of structures during earthquakes became an important issue in the last decades because the trepidations that manifest on a large area around the epicenter cause damages to the infrastructure and can result in human losses [1-3]. Advancements in seismic isolation were made in the last decades, now being available solutions that ensure good results in reducing the effects of the earthquakes [4-6]. Inserting elastomeric elements between the ground and the foundation of the structure had become a common solution [7]. An analysis of the behavior of laminated elastic elements consisting of rubber and steel sheets is made in [8]. The effect of a supplementary added lead core to the laminated steel-rubber bearings is investigated in [9]. A highly nonlinear effect is obtained if an elastomeric bearing is combined with a lead-rubber bearing resulting in the so-called hybrid lead rubber bearing [10]. Models of such rubber bearings describing their specific behavior are available [11-13]. To develop reliable analytical and numerical models, it is important to know the non-linear behavior of the elastic layer constituted by rubber or neoprene [14].
A particular seismic isolation device that is based on the dissipation of the earthquake-induced energy by friction is now used for several decades [15]. This device, known as the friction pendulum (FP), has proved its maturity. However, a lot of research concerns the improvement of controlling the response of the isolated structure. To this aim, pendulums with more than one sliding surfaces are now developed [16]. A new trend in the design of FPs is the use of adaptive sliding surfaces such as those based on polynomial curves [17, 18].
Our previous studies focused on finding the response of structures isolated with FPs that have different radii, friction coefficients and are subjected to harmonic or random excitation [19]. Experiments are also made on a special shaking table developed in our laboratory [20]. The study we describe in the following aimed to find the influence of the curvature of the sliding surface on the response of the isolated structure under harmonic excitations.
2. Materials and methods
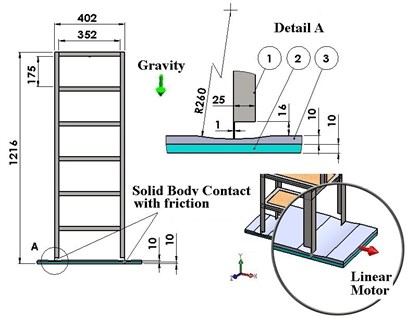
To obtain the response of a five-story rigid structure isolated with diverse FPs, we performed simulations with SolidWorks, in particular by using the Motion module. The isolated structure’s 3D geometrical model, described in Fig. 1, is similar to that presented in [19]. The assembly consists of three parts: (1) the rigid structure; (2) the base plate used as a reference; (3) the shaking plate simulating the horizontal trepidation of the earth. The latter component includes also the FPs.
The rigid structure is made of steel profile with the following dimensions of the cross-section: size 25 mm and the thickness 1 mm. The main dimensions of the assembly are indicated in Fig. 1.
Simulations are made in the following conditions:
a) The base plate, which is set as a reference, is fixed.
b) The shaking plate simulating the horizontal trepidation of the earth is harmonically moved in the direction. This is made with the help of the Linear Motor, a feature of SolidWorks Motion module. It imposes a Max Displacement 10 mm by a Frequency 1 Hz.
c) The gravitational acceleration is set by default as 9806.65 mm/s2 and is oriented in the direction.
d) The time for this study is imposed as 30 seconds.
In this study, the mentioned parameters are maintained unchanged, but the radii of the sliding surfaces are modified by each simulation. However, for all simulations these are modeled as an extrusion applied to the shaking plate.
Fig. 1The assembly modeled in SolidWorks
For the first set of simulations, the base of the cylinder used for extrusion is a circle, the radius being modified in the range 110/960 mm by a 50 mm pitch. The depth of the extrusion is 4 mm, therefore the minimum thickness of the shaking plate under the pendulum is 6 mm. A suggestive image showing all radii used to create of the FP is given in Fig. 2.
Table 1Contact condition based on friction coefficients
Contact case | Components | Contact type | [–] | [mm/s2] | [–] | [mm/s2] |
1 | Structure | Steel (dry) | 0.25 | 10.16 | 0.3 | 0.1 |
Shaking plate | Steel (dry) | |||||
2 | Structure | Steel (greasy) | 0.05 | 10.16 | 0.08 | 0.1 |
Shaking plate | Steel (greasy) | |||||
3 | Structure | Teflon | 0.03 | 10.16 | 0.05 | 0.1 |
Shaking plate | Steel (greasy) |
The contact condition between the structure and the sliding surface is bounded contact with friction, the friction coefficient being dependent of the chosen materials. Note that the friction coefficient depend on the relative speed beteen the two components in contact. We took the values for the first two cases in Table 1 from the SolidWorks library, while for the third case we defined the values to achieve a lower damping.
Fig. 2The extrusions made with a circular shape
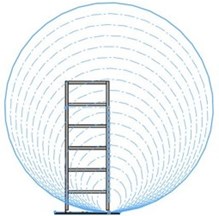
a)
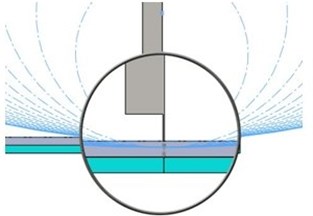
b)
In the absence of friction between the structure and the sliding surface, the natural frequency of a rigid structure isolated with a FP is found from the mathematical relation:
From Eq. (1) clearly results that is independent of the weight of the structure. If subjected to a harmonic excitation , the structure oscillates in respect to the two mentioned frequencies. When the relation between the two frequencies is , the frequency of the structure is the frequency of the excitation. If , the system maintain its natural frequency no matter how big the frequency of the excitation is. When the two amplitudes achieve close values, the amplitude of the oscillation increases dramatically, and for equal frequencies the resonance is attained. The amplitude resulted in resonance depends on the friction coefficient; the smaller the friction coefficient, the bigger the amplitude is.
For the second set of simulations, we use for extrusion cylinders that have ellipses at the base. The vertically radius of the ellipse is always 960 mm, while the horizontally radius is modified in the range 110/960 mm by a 50 mm pitch, as shown in Fig. 3.
Fig. 3The extrusions made with an elliptical shape

a)
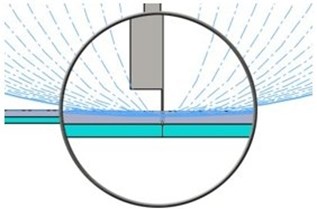
b)
Because the slope of the sliding surface is significantly bigger for the case ellipse 110-960 than for the case radius 110, we expect in the case of the sliding surface having constructed with an elliptical cylinder to get no relative displacement between the structure and the shaking plate. We also expect to achieve the resonance at higher values of the horizontal radius of the ellipse as the radius of the cylinder.
It is no relation presented in the literature for determining the natural frequency of the elliptical FP, thus the behavior in terms of frequencies and amplitudes of the oscillation of the isolated structure cannot be predicted. By the simulations performed with elliptical FPs, we intend to clarify this aspect.
3. Results and discussions
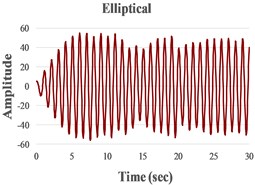
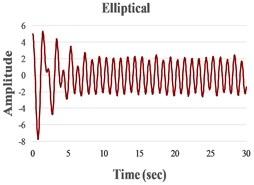
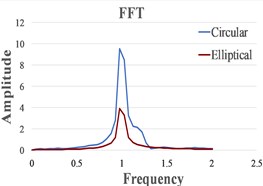
We present in Fig. 4 the signals in the time domain and the frequency domain (by FFT representation) for three typical behaviors of both the FPs. In the left column in this figure we represented the analysis for a pre-resonance behavior, in the central column the behavior in resonance and in the right column the behavior in post-resonance. The friction coefficient is chosen for the contact case 1 (steel dry – steel dry).
Fig. 4Response signal captured from the isolated structure for different friction pendulum radii
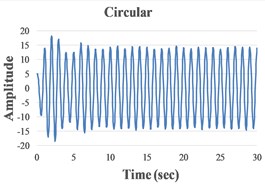
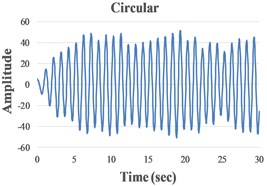
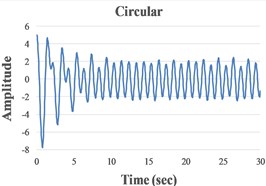
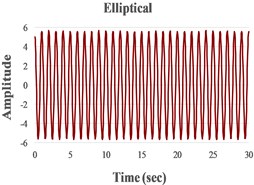
a) 160 mm
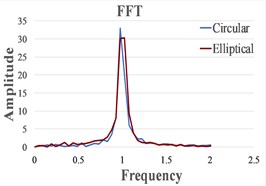
b) 260 mm, 460 mm
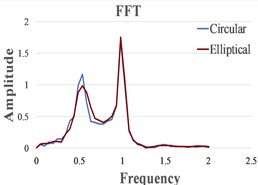
c) 910 mm
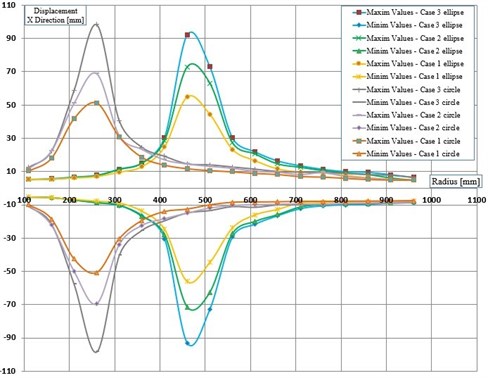
In Fig. 5 we offer a comprehensive image on the behavior of the structures when it is isolated with FPs that have all considered radii and both circular and elliptic cylindrical shapes. In this figure, the minim and maxim values of the structure’s displacements in the direction are indicated in order to show for which horizontal radii the resonance is achieved.
One can observe in Fig. 5 that, as expected, the resonance is achieved for smaller values of in comparison with . This determines a bigger pre-resonance domain for the elliptical FP, while the post-resonance is earlier achieved by the FP constructed with a circular cylindrical sliding surface. The magnitudes of the curves represented in Fig. 5 are quite similar for similar friction coefficients. Because the magnitudes are extracted from the signals by involving the FFT, just coarse values are obtained. To precisely estimate the magnitudes an advanced signal processing algorithm is requested [21].
Fig. 5Maximum and minimum displacement amplitudes
4. Conclusions
The paper presents a comparison between the responses of a structure isolated by different types of friction pendulums. We found that it is possible to control the occurrence of resonance by changing the horizontal radius of the ellipse, therefore it is possible to design the FP in order to work in pre- or post-resonance depending on the parameters (frequency and amplitude) expected for the ground excitation. For both set of pendulums we concluded that the best isolation of the structure is achieved when the natural frequency of the pendulum is at least 1.5 times lower than the ground excitation. We also found that the friction coefficient has the same influence on the amplitudes of the structure’s response it the FP has the same natural frequency. This is best visualized at resonance, the curves in Fig. 5 achieving approximately the same magnitude. Our next research will focus on finding a relationship to express the natural frequency of elliptical friction pendulums.
References
-
Skinnr R. I., Robinson W. H., Mcverry G. H. An Introduction to Seismic Isolation. John Wiley and Sons, London, 1993.
-
Nola I. A. Earthquakes and their environmental, medical and public health impacts. Salud Publica de Mexico, Vol. 60, 2018, p. 16-22.
-
Sinha A. K., Kumar S. Economic consequences of earthquakes. International Journal of Research in Chemical, Metallurgical and Civil Engineering, Vol. 4, Issue 1, 2017, p. 84-88.
-
Tsai C. S. Advanced base isolation systems for light weight equipments. Earthquake-Resistant Structures-Design, Assessment and Rehabilitation, Intech, 2012, p. 79-130.
-
Wilde K., Garboni P., Fujino Y. Base isolation system with shape memory alloy device for elevated highway bridges. Engineering Structures, Vol. 22, Issue 3, 2000, p. 222-229.
-
Morgan T. A., Mahin S. A. achieving reliable seismic performance enhancement using multi-stage friction pendulum isolators. Earthquake Engineering and Structural Dynamics, Vol. 39, 2010, p. 1443-1461.
-
Kelly J. M. Earthquake-Resistant Design with Rubber. 2nd Edition, Springer-Verlag, London, 1997.
-
Lejeunes S., Boukamel A., Cochelin B. Analysis of laminated rubber bearings with a numerical reduction model method. Archive of Applied Mechanics, Vol. 76, Issues 5-6, 2006, p. 311-326.
-
Hameed A., Koo M.-S., Do T. D., Jeong J.-H. Effect of lead rubber bearing characteristics on the response of seismic-isolated bridges. KSCE Journal of Civil Engineering, Vol. 12, 2008, p. 187-196.
-
Tanaka K., Hirasawa M., Ishiguro Y., Ohyama H., Nakamura Y. Base-isolation system with hybrid lead rubber bearings. International Conference on Structural Mechanics in Reactor Technology; Stuttgart, Germany, 1993.
-
Iancu V., Vasile O., Gillich G. R. Modelling and characterization of hybrid rubber-based earthquake isolation systems. Materiale Plastice, Vol. 49, Issue 4, 2012, p. 237-241.
-
Doudoumis I. N., Gravalas F., Doudoumis N. I. Analytical modeling of elastomeric lead-rubber bearings with the use of finite element micromodels. 5th GRACM International Congress on Computational Mechanics, Limassol, 2005.
-
Iancu V., Gillich G. R., Iavornic C. M., Gillich N. Some models of elastomeric seismic isolation devices. Applied Mechanics and Materials, Vol. 430, 2013, p. 356-361.
-
Gillich G. R., Samoilescu G., Berinde F., Chioncel C. P. Experimental determination of the rubber dynamic rigidity and elasticity module by time-frequency measurements. Materiale Plastice, Vol. 44, Issue 1, 2007, p. 18-21.
-
Zayas V. A., Low S. S., Mahin S. A. A simple pendulum technique for achieving seismic isolation. Earthquake Spectra, Vol. 6, 1990, p. 317-333.
-
Tsai C. S., Lin Y. C., Su H. C. Characterization and modeling of multiple friction pendulum isolation system with numerous sliding interfaces. Earthquake Engineering and Structural Dynamics, Vol. 39, Issue 13, 2010, p. 1463-1491.
-
Minda A. A., Gillich G. R., Iavornic C. M., Minda P. F. Analytical and finite element study for friction pendulum with parameterized sliding surfaces. Proceedings of the World Congress on Engineering, London, 2012.
-
Lu L.-Y., Lee T.-Y., Juang S.-Y., Yeh S.-W. Polynomial friction pendulum isolators (PFPIs) for building floor isolation: an experimental and theoretical study. Engineering Structures, Vol. 56, 2013, p. 970-982.
-
Nedelcu D., Iancu V., Gillich G. R., Bogdan S. L. Study on the effect of the friction coefficient on the response of structures isolated with friction pendulums. Vibroengineering Procedia, Vol. 19, 2018, p. 6-11.
-
Iancu V., Galuska I., Mănescu T. Shaking table for the analysis of pillars with top mass. 14th International Symposium Acoustics and Vibrations of Mechanical Structures Timisoara, Romania, Vol. 198, 2017, p. 405-410.
-
Gillich N., Mituletu I. C., Gillich G. R., Chioncel C. P., Hatiegan C. Frequency and magnitude estimation in voltage unbalanced power systems. 10th International Symposium on Advanced Topics in Electrical Engineering, Bucharest, 2017.
