Abstract
The aim of the structural health monitoring (SHM) is to provide useful information about the state of the structures. However, the data collected from monitoring needs to be first translated into actionable, quantitative or qualitative based characteristics, that indicate the condition of a bridge. The paper proposes a methodology for comparison of regularly measured data to monitor the state of stringers and floorbeams. Also, the dynamic factor is evaluated and compared with code values.
1. Introduction
A condition of bridges deteriorates with increased age and to ensure their safety and serviceability, inspections are performed regularly. However, a decision about when, how and what part of a bridge needs to be repaired is a common and difficult management task. Additional information to support these decisions can be provided by structural health monitoring (SHM) [1, 2].
The paper presents a methodology based on a comparison of measured data and calculated stresses using a simplified model of passing train. An index is proposed to track the state of selected stingers and floorbeams, which are usually one of the structural elements most prone to corrosion and fatigue cracks. Its value is based on results from an updated and verified FE model and response of the real structure measured by strain gauges. There are several case studies of SHM on bridges, where the strain was measured on different structural elements [3-6]. The work was also based on past experiences with test and measurements of various bridges [7, 8].
2. Structure and test description
The structure is a steel railway bridge located in northern Slovakia over the river Vah. It consists of three simple supported objects (Fig. 1): a truss with a span of 57,4 m (O2) and two girder bridges at sides with a span of 29,4 m (O1, O3).
Fig. 1One of the tested bridges (T2) and the location of sensor S1 on the upper flange of a stringer
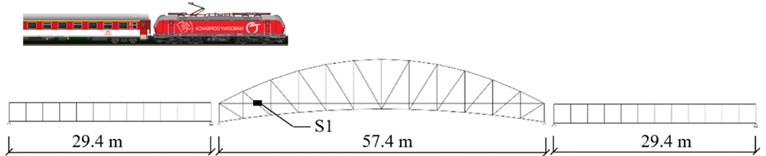
Sleepers are directly connected to stringers, whose spans are 4,2 m and 4,9 m (O2) or 2,45 m (O1, O3). Stringers, floorbeams and main girders are attached with riveted double angle connection.
To measure the response of a structure caused by passing trains, strain gauges were applied to selected flanges of stringers and floorbeams. Data was also collected by accelerometers, interferometric radar, temperature sensors and video recorder.
3. Reduction of load parameters
In engineering practice, a method is often used when we try to neglect input parameters that have little effect on the accuracy of results. We used the same principle in this work. In order to compare the effects caused by passing of different trains, we looked for a simplified load model that significantly influences the stresses in the measured cross-sections. First, an important assumption is made that the weight of the locomotive is about two times greater than the weight of the passenger wagons.
Given the size of the bridge spans (around 50-60 m) and the length of the train (up to 200 m), it seems it is most important to know the locomotive’s parameters in the first phase of the train passage, unless the locomotive (with the length about 16 m) is not further than in the middle of the span (Fig. 1) and behind it there is only one wagon or even only portion of it (with the length about 26 m).
In addition, we can quite easily find out all the characteristics of locomotives (dimensions, weights, axle distances and others) that are operated across Slovakia and therefore it is easy to identify its type and speed. This can be done from the video we make with each measurement. In addition, the weight of the locomotive does not change during its entire service life. Then the weight of the wagon, though only estimated (depending on the number of passengers), has little effect on the measured values. Thus, we can accurately determine the load on the bridge and use it in the numerical calculation we need for comparison.
This assumption can be used not only for checking the stresses in stingers and floorbeams near to the support but also for checking the deflection functions of the bridge.
4. Comparison of measured and calculated data
The measurements were carried out during normal operating conditions with a high diversity of passing trains (passenger, regional, inter-city, freight…). Our aim was to find a methodology of how to compare measured time histories and detect changes in structural response. First, the values of strains were transformed to dimensionless quantity, independent of characteristics of passing train. The static loading forces from a train vehicle were defined thanks to the known values of the weight on axle and distances between axles. Then, influence lines were calculated using static analysis of a verified FEM model. As a result, the peak values of normal stresses from a passing train were obtained.
These values were then compared with peak values of stresses gained from strain data and index was expressed by Eq. (1):
where the numerator is a peak value of normal stress calculated from influence lines and the denominator is a peak value of normal stress obtained from the measurement. Quantity /2 refers to load on a wheel, and are ordinates of influence line in a location of axles (Fig. 2). Measured strain values are multiplied by Young’s modulus to acquire stress values.
As seen in Table 1 presenting the results of regular measurements for sensor S1, the index takes values close to 1. This proves, that a complex, precisely calibrated FEM model accurately representing real behavior of a structure was successfully prepared.
Fig. 2Influence lines of normal stress for the location of sensor S1 (bridge T2-O2) and its evaluation in case of locomotive 363
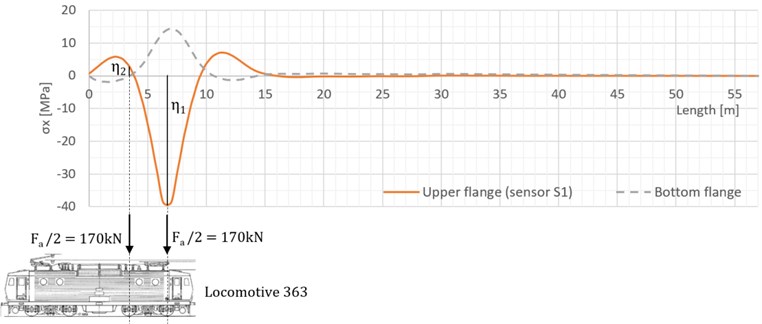
Table 1Evaluation of strain measurements from sensor S1 (bridge T2-O2)
Test No. | Train No. | Type of locomotive | Wheelbase [m] | Axel weight [t] | Velocity [km/h] | [MPa] | [MPa] | [–] | [–] |
1 | R953 | 757 | 2,4 | 18,85 | 75 | 10,5 | 11,2 | 1,07 | 0,96 |
2 | IC523 | 383 | 3,0 | 22,25 | 78 | 9,45 | 10,5 | 1,11 | 1,03 |
5. Measured vs. code value of a dynamic factor
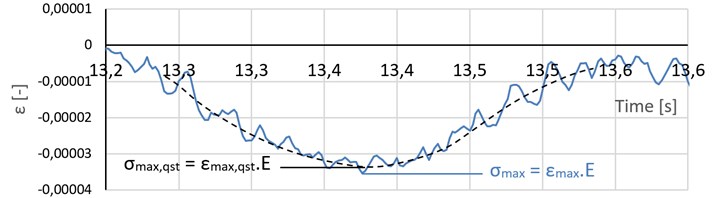
A dynamic factor was evaluated from measured strain time histories according to Eq. (2):
where is a maximum value of stresses with dynamic effects and is a maximum of quasi-static stresses (Fig. 3).
As shown in Table 1, the dynamic factor for selected stringer takes values around 1,10.
Fig. 3Determining maximum dynamic and quasi-static effects of a passing train.
When assessing the loading capacity of existing bridges, a dynamic amplification factor (DAF) is one of the most important characteristics to consider. In practice, its value is determined according to an internal code of Railways of the Slovak Republic [9] and it represents the dynamic effects of passing trains. For tracks with standard maintenance, DAF is considered as (Eq. (3)):
where is DAF and , depend on the value of the first natural frequency of unloaded bridge.
The guidelines [9] also include a table with DAF as a function of determinant length and velocity, where it takes values up to 2,00. However, our experiences from in-situ tests reveals, that values of the dynamic factor for the selected stringer are much smaller (approx. 1,10) and the code estimation is too conservative.
Therefore, we recommend to consider experimental DAF values from measurements on a real structure during assessment, rather than the code values, to detect reserves in load capacity of the bridge.
6. Conclusions
A simplified model of passing trains has been considered to obtain numerical results with sufficient accuracy. These calculations have been subsequently compared with strain measurements and the results show a good agreement. The proposed methodology has allowed us to compare measured time histories from regular testing campaigns and monitor potential changes in the structural response of selected stringers and floorbeams. Also, a dynamic factor has been evaluated and it has been demonstrated, that experimentally achieved values should be used for load capacity assessments, rather than too conservative code values.
References
-
Zonta D., Glisic B., Adriaenssens S. Value of information: Impact of monitoring on decision-making. Structural Control and Health Monitoring, Vol. 21, Issue 7, 2014, p. 1043-1056.
-
Lynch J., Farrar C., Michaels J. structural health monitoring: technological advances to practical implementations. Proceedings of the IEEE, Vol. 104, Issue 8, 2016, p. 1508-1512.
-
Ahlborn T. M., et al. The State-of-the-Practice of Modern Structural Health Monitoring for Bridges: A Comprehensive Review. Michigan Tech, Michigan, 2010.
-
Leander J., Andersson A., Karoumi R. Monitoring and enhanced fatigue evaluation of a steel railway bridge. Engineering Structures, Vol. 32, 2010, p. 854-863.
-
Zhang J., et al. Structural health monitoring of a steel stringer bridge with area sensing. Structure and Infrastructure Engineering, Vol. 10, Issue 8, 2013, p. 1049-1058.
-
Ye X. W., Ni Y. Q., Wong K. Y., Ko J. M. Statistical analysis of stress spectra for fatigue life assessment of steel bridges with structural health monitoring data. Engineering Structures, Vol. 45, 2012, p. 166-476.
-
Ároch R., Sokol M., Venglár M. Structural health monitoring of major Danube bridges in Bratislava. Procedia Engineering, Vol. 156, 2016, p. 24-31.
-
Sokol M., et al. Traffic response pattern of cable-stayed bridge as a comparison tool for SHM. 39th IABSE Symposium – Engineering the Future, Canada, 2017, p. 191-197.
-
General Technical Requirements: Determination of the Railway Bridges Loading Capacity. Railways of the Slovak Republic, 2016.
About this article
This paper has been supported by the Grant No. 1/0749/19 provided by VEGA Agency of Ministry of Education, Science, Research and Sport of the Slovak Republic. It was also supported by grant from research program of Slovak University of Technology – Excellent teams of young researchers 2018.
