A novel faults detection method for rolling bearing based on RCMDE and ISVM

Zhang, Xin; Zhao, Jianmin; Teng, Hongzhi; Liu, Guozeng

doi:10.21595/jve.2019.20815

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 December 2019

Check for updates

A novel faults detection method for rolling bearing based on RCMDE and ISVM

Xin Zhang¹

Jianmin Zhao²

Hongzhi Teng³

Guozeng Liu⁴

^{1, 2, 4}Army Engineering University, Shijiazhuang, China

³Army 32180 Unite, Beijing, China

Corresponding Author:

Xin Zhang

Cite the article Download PDF

Downloads 1281

WoS Core Citations 11

CrossRef Citations 12

Abstract

The rolling bearing is an essential element widely used in the rotating machinery. Bearing failures are among the main reasons for breakdown of rotating machinery. Therefore, fault detection of bearing is necessary to reduce the probability of breakdown and safety accidents. A novel fault diagnosis method for rolling bearing based on Refined Composite Multiscale Dispersion Entropy (RCMDE) and Improved Support Vector Machine (ISVM) is presented in this paper. The RCMDE is a new irregular index in biomedical signal analysis, which has lower computational cost and more stable results. Therefore, the RCMDE is introduced as fault feature to represent the bearing fault characteristics. After feature extraction, an improved support vector machine based on whale optimization algorithm (WOA) and support vector machine (SVM) is proposed as a fault classifier, which has the advantages of less training samples and good classification effect. The effectiveness of the proposed method in bearing fault diagnosis is verified by using bearing fault experimental data.

Highlights

The Refined Composite Multiscale Dispersion Entropy is introduced as fault feature to represent the bearing fault characteristics
Improved support vector machine based on whale optimization algorithm (WOA) and support vector machine (SVM) is proposed as a fault classifier
A novel fault diagnosis method for rolling bearing based on Refined Composite Multiscale Dispersion Entropy (RCMDE) and Improved Support Vector Machine (ISVM) is presented

1. Introduction

The rolling bearing plays an important role in rotating machinery and transmission machinery system. The working environment of rolling bearings is usually odious and sophisticated, which leads to the fault more easily occurring in rolling bearings. According to incomplete statistics, about 30 % of the faults occur in rotating machinery equipped with rolling bearings are caused by the faults of rolling bearings, and many major safety accidents are caused by the damage of bearings. Therefore, it is necessary to develop the method of rolling bearing fault diagnosis.

So far, many methods have been proposed and applied to bearing fault diagnosis. According to the source of the signal, the method can be divided into the following categories, such as vibration analysis [1, 2], oil analysis [3, 4], infrared thermal imaging [5-7] and acoustic emission analysis [8-10]. Compared with other methods, the signal acquisition and analysis of vibration analysis are easier to implement. Therefore, various vibration analysis methods have been introduced in fault diagnosis of rolling bearings, such as autoregressive model [11, 12], spectral kurtosis [13-15] and kurtogram [16], wavelet transform [17, 18], matching pursuit order tracking [19, 20] and empirical mode decomposition [21, 22]. Although the above methods have been proved to be effective tools of fault diagnosis for rolling bearings, but the process of these methods is not simple enough, which is not conducive to the practical application of engineering. Aiming at the shortages of above methods, an intelligent fault diagnosis method for rolling bearings based on refined composite multiscale dispersion entropy (RCMDE) and improved support vector machine (ISVM) is proposed in this paper.

The RCMDE is extracted as bearing fault feature in the proposed method. The RCMDE is a new irregular index proposed by Azami [23] and applied it to biomedical signal analysis. Compared with multi-scale sample entropy [24] and multi-scale fuzzy entropy [25], RCMDE has lower computational cost and more stable results. For these reasons, the RCMDE is a simple and effective feature extraction method which has more potential to be applied in engineering practice. Therefore, the RCMDE is proposed as a feature parameter reflecting fault state of rolling bearings. After fault features extraction, the improved support vector machine (ISVM) based on whale optimization algorithm (WOA) [26] and support vector machine (SVM) is proposed as fault classifier for rolling bearings. The SVM has the advantages of fewer training samples and faster calculation speed, which is beneficial to the practical application of engineering. The change of regularization factor and kernel parameter of support vector machine will determine the performance of classification. Therefore, this paper proposes an improved support vector machine (ISVM) whose parameters are optimized by WOA.

The Fig. 1 illustrates the framework diagram of the proposed method. Firstly, the original bearing fault signal is collected from rolling bearing fault test rig by sensors. Then the RCMDE values of vibration signals are calculated to form eigenvectors as the input of ISVM. Subsequently, the ISVM is trained by using training data and the ISVM optimal model is obtained. Finally, the ISVM optimal model is used to classify the test data, and the fault diagnosis results are obtained.

Fig. 1Framework diagram of proposed method

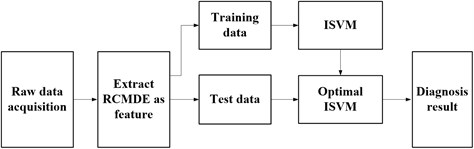
The article is arranged as follows. The theory of refined composite multiscale dispersion entropy (RCMDE) is introduced in Section 2. Section 3 describes the improved support vector machine (ISVM) based on whale optimization algorithm (WOA) proposed in this paper. Section 4 investigates the effectiveness of the proposed method through experimental data. And the conclusions are drawn in Section 5.

2. Refined composite multiscale dispersion entropy

2.1. Multiscale dispersion entropy

Firstly, the calculation process of multiscale dispersion entropy is introduced in this section. For the initial time series $u = \{u_{1}, u_{2}, \dots, u_{L}\}$ , where the $L$ is the length of the time series. Then the initial time series u is divided into non-overlapping segments of length $τ$ , which is called scale factor. The average of each segment is calculated, and the coarse-grained signal with scale factor $τ$ is obtained as follows:

1

{x_{j}}^{τ} = \frac{1}{τ} \sum_{b = (j - 1) τ + 1}^{j τ} u_{b}, 1 \leq j \leq ⌊\frac{L}{τ}⌋ = N .

After coarsening, the dispersion entropy is calculated for each coarsening sequence. Similar to sample entropy and permutation entropy, the dispersion entropy is an algorithm to measure the complexity or irregularity of time series. The larger the dispersion entropy, the higher the degree of irregularity, the smaller the dispersion entropy and the lower the degree of irregularity. For a given time series of length $N$ : $x = \{x_{1}, x_{2}, \dots, x_{N}\}$ , the calculation steps of dispersion entropy are as follows.

(1) Mapping time series $x$ into $y = \{y_{1}, y_{2}, \dots, y_{N}\}$ from 0 to 1 using normal distribution function as follows:

2

y_{i} = \frac{1}{σ \sqrt{2 π}} \int_{- \infty}^{x_{j}} e^{\frac{- (t - μ)^{2}}{2 σ^{2}}} d t,

where $μ$ and $σ^{2}$ represent expectation and variance respectively.

(2) The $y$ is mapped to the range of {1, 2, …, $c$ } by linear transformation as follows:

3

z_{j}^{c} = R (c \cdot y_{j} + 0.5),

where $R$ is an integral function and $c$ is the number of categories.

(3) Then calculate the embedding vector as follows:

4

z_{i}^{m, c} = \{z_{i}^{c}, z_{i + d}^{c}, \cdot \cdot \cdot, z_{i + (m - 1) d}^{c}\}, i = 1,2, \cdot \cdot \cdot, N - (m - 1) d .

Among them, $m$ and $d$ are embedding dimension and time delay respectively.

(4) The dispersion pattern $π_{v_{0} v_{1} \cdot \cdot \cdot v_{_{m - 1}}} (v = 1,2, \cdot \cdot \cdot, c)$ is calculated. The corresponding dispersion pattern of $z_{i}^{m, c}$ is $π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}}$ if $z_{i}^{c} = v_{0}$ , $z_{i + d}^{c} = v_{1}, \cdot \cdot \cdot z_{i + (m - 1) d}^{} = v_{m - 1}$ . Since $π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}}$ consists of $c$ digits and each digit has $m$ values, the corresponding dispersion patterns have c^m values.

(5) Calculate the probability $p (π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}})$ of each dispersion pattern $π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}}$ as follows:

5

p (π_{v_{0}, v_{1} \cdot \cdot \cdot, v_{m - 1}}) = \frac{N u m b e r (π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}})}{N - (m - 1) d},

where $N u m b e r (π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}})$ represents the number of mappings from $z_{i}^{m, c}$ to $π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}}$ .

(6) According to the definition of Shannon Entropy, the dispersion entropy of the original signal is defined as follows:

6

D E (x, m, c, d) = - \sum_{π = 1}^{c^{m}} p (π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}}) l n (p (π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}})) .

It can be seen from the algorithm of dispersion entropy that when all dispersion entropy patterns have the same probability, dispersion entropy achieves the maximum value of $l n (c^{m})$ , such as noise signal. Conversely, when only one $p (π_{v_{0}, v_{1}, \cdot \cdot \cdot, v_{m - 1}})$ value is not equal to zero, the time series is a completely regular or predictable data, and the dispersion entropy value is the smallest, such as periodic signals.

2.2. Refined composite multiscale dispersion entropy

The calculation steps of RCMDE are shown as follows.

For the original data $u$ , the $k$ th coarsening sequence $x_{k}^{τ} = {x_{k, 1}^{τ}, x_{k, 2}^{τ}, \cdot \cdot \cdot}$ can be obtained as follows:

7

x_{k, j}^{τ} = \frac{1}{τ} \sum_{b = k + τ (j - 1)}^{k + j τ - 1} u_{b}, 1 \leq j \leq \frac{L}{τ}, 1 \leq k \leq τ .

For each scale $τ$ , RCMDE is defined as follows:

8

R C M D E (x, m, c, d, τ) = - \sum_{π = 1}^{c^{m}} \bar{p} (π_{v_{0} v_{1} \cdot \cdot \cdot v_{m - 1}}) \cdot \ln (\bar{p} (π_{v_{0} v_{1} \cdot \cdot \cdot v_{m - 1}})),

where $\bar{p} (π_{v_{0} v_{1} \cdot \cdot \cdot v_{m - 1}}) = \frac{1}{τ} \sum_{1}^{τ} p_{k}^{τ}$ is the average probability of the dispersion pattern $π$ of the coarse-grained sequences $x_{k}^{τ}$ .

3. The improved support vector machine based on whale optimization algorithm

The support vector machine (SVM) is a binary classification model. Its purpose is to find a hyperplane to segment samples. The principle of segmentation is to maximize the interval, and finally to solve a convex quadratic programming problem. Because the bearing fault data are nonlinear, the improved support vector machine is proposed on the basis of nonlinear support vector machine. Suppose there is a training data set $D = {x_{i}, y_{i}}_{i = 1}^{n}$ , where $x_{i} \in R^{n}$ is the $i$ -th input feature vectors, $n$ is the total number of samples, $y_{i} \in {+ 1, - 1}$ is the category label of $x_{i}$ According to the definition of support vector machine, the following conditions should be satisfied in order to establish the optimal classification hyperplane:

9

\{\begin{array}{l} w \cdot x_{i} + b \geq + 1 - ξ_{i} & y_{i} = + 1, \\ w \cdot x_{i} + b \geq - 1 + ξ_{i} & y_{i} = - 1 . \end{array}

Simplify and amalqamate the above two constraints into:

10

y_{i} [(w \cdot x_{i}) + b] - 1 + ξ_{i} \geq 0, i = 1,2, \cdot \cdot \cdot, n,

where $ξ_{i} \geq 0$ is the slack variables, $b$ is a scalar and the $w$ is weight vector. When the input $x_{i}$ is nonlinear, a new high-dimensional feature set needs to be obtained $ϕ (x_{i})$ by nonlinear mapping $φ$ . Thus, by introducing the obtained high-dimensional feature set $ϕ (x_{i})$ into Eq. (10), the following constraints can be obtained:

11

y_{i} [(w \cdot ϕ (x_{i})) + b] - 1 + ξ_{i} \geq 0, i = 1,2, \cdot \cdot \cdot, n .

The objective function for finding the optimal classification hyperplane is:

12

m i n \frac{1}{2} w^{T} w + C \sum_{i = 1}^{n} ξ_{i},

where $C$ is the regularization parameter. The regularization parameter is used to weigh the relationship between empirical risk and complexity. In order to solve this problem, Lagrange function is introduced and the following results are obtained:

13

L (w, b, ξ, α, β) = \frac{1}{2} w^{T} w + C \sum_{i = 1}^{n} ξ_{i} - \sum_{i = 1}^{n} β_{i} ξ_{i} - \sum_{i = 1}^{n} α_{i} [y_{i} ((w \cdot ϕ (x_{i})) + b) + ξ_{i} - 1],

where $α_{i} \geq 0$ , $β_{i} \geq 0$ are Lagrange multipliers. For Eq. (8), the partial derivatives of $w$ , $b$ and $ξ_{i}$ are calculated and made equal to 0. After calculation, the following formulas are obtained:

14

L (w, b, ξ, α, β) = \sum_{i = 1}^{n} α_{i} - \frac{1}{2} \sum_{i = 1}^{n} \sum_{j = 1}^{n} α_{i} α_{j} y_{i} y_{j} [φ (x_{i}) \cdot φ (x_{j})] .

According to the Karush-Kuhn-Tucker (KKT) condition, the following conditions are needed to solve this optimization problem:

15

\{\begin{array}{l} α_{i} [y_{i} ((w \cdot ϕ (x_{i})) + b) + ξ_{i} - 1] = 0, \\ β_{i} ξ_{i} = 0 \Rightarrow (C - α_{i}) ξ_{i} = 0, i = 1,2, \cdot \cdot \cdot, n . \end{array}

The inner product in the feature space can be replaced by according to the Mercer condition. Thus, the above problems can be transformed into the following binary programming problems:

16

m a x \sum_{i = 1}^{n} α_{i} - \frac{1}{2} \sum_{i = 1}^{n} \sum_{j = 1}^{n} α_{i} α_{j} y_{i} y_{j} K (x_{i}, x_{j}),

s . t . \{\begin{array}{l} \sum_{i = 1}^{n} y_{i} α_{i} = 0, \\ 0 \leq α_{i} \leq C, i = 1,2, \cdot \cdot \cdot, n . \end{array}

After solving the above problem, the optimal classification function is obtained as follows:

17

f (x) = s g n [\sum_{i = 1}^{n} α_{i} y_{i} K (x_{i}, x) + b] .

In this paper, the kernel function of support vector machine is radial basis function (RBF). the kernel function is shown as follows:

18

K (x_{i}, x) = e x p (γ {‖x_{i} - x‖}^{2}), γ > 0,

where $γ$ is the kernel parameter.

Fig. 2Flow chart for optimization of ISVM

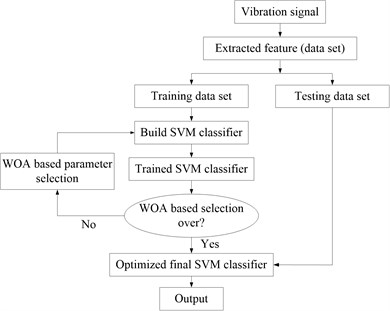
The RBF kernel parameter $γ$ and regularization parameter $C$ mentioned above are important parameters of support vector machine, and their selection will determine the classification performance of support vector machine. In order to improve the classification effect of traditional support vector machine, this paper proposes an improved support vector machine whose parameters are optimized by WOA. The WOA is a meta-heuristic optimization algorithm proposed by Mirjalili in 2016. It has the characteristics of fast optimization speed and good optimization effect. Specific description of WOA can be referred to in literature [26]. In this paper, a fitness function is proposed to evaluate the optimization effect of the algorithm. The fitness function can be calculated as follows:

19

F_{f i t} (C_{i}, γ_{i}) = 1 - \frac{1}{1 + a_{v c} (C_{i}, γ_{i})},

where $a_{v c} (C_{i}, γ_{i}) \in [0,1]$ is the cross validation accuracy of SVM using the parameters $C_{i}$ and $γ_{i}$ . The parameter optimization process of the improved support vector machine presented in this paper is presented in Fig. 2.

4. Case study 1

In this section, the fault data of the Case Western Reserve University are employed to verify the performance of the proposed means in bearing fault detection, and the test rig is presented in the Fig. 3. The test rig consists of a motor, a torque sensor, a power tester and an electronic controller. In the case, the type of fault bearing is SKF6205. The data includes four states: normal state, inner ring fault, outer ring fault and rolling element fault. The inner ring fault, outer ring fault and rolling element fault have several sizes of 0.007 inches, 0.014 inches and 0.028 inches respectively. Usually, bearing faults with smaller sizes are difficult to identify, so the fault data of 0.007 inches size are selected to verify the proposed method. If the fault state data of small size can be correctly identified via the proposed method, it shows that the fault state data of other sizes can also be identified by the proposed method. All the vibration data of fault bearing was recorded for motor loads of 0 to 3 horsepower (motor speeds of 1797 to 1720 RPM). In the case, the data under all working conditions are mixed together and identified by the proposed method. The data of each state is divided into 40 samples, a total of 160 samples. Among them, 64 samples were used as training samples and the remaining 96 samples were used as test sample.

Fig. 3Structure of test rig

Referring to the setting of RCMDE parameters in literature 12, the embedding dimension $m$ , time delay $d$ and number of classes $c$ are set to 1, 1 and 6 respectively. The scale factor of RCMDE is set to 5 in the case study. After calculation, the RCMDE value of the training sample is shown in the Fig. 4. As shown in the Fig. 4, RCMDE value of four states can be roughly distinguished under different scale factors.

Table 1Input parameters of WOA in ISVM

Parameters	Value
Number of whales population	50
Maximum number of iterations	100
Parameter lower bound	0.0001
Parameter upper bound	100
Number of cross validation	3

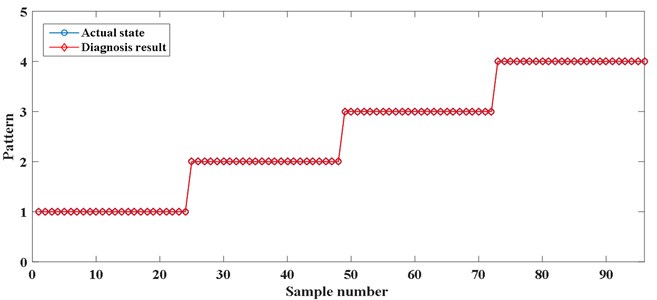
After calculating RCMDE, the feature vector composed of RCMDE is extracted as the input of ISVM. Then the training samples are used to train the ISVM to obtain the optimal ISVM classification model. The WOA parameter settings in the ISVM are shown in the Table 1. The optimized kernel parameter $γ$ and regularization parameter $C$ are 4.5817 and 2.4198 respectively after optimization. The diagnosis result is presented in the Fig. 5. As shown in the Fig. 5, the fault diagnosis results are in good agreement with the actual state. After calculated, the recognition accuracy of bearing fault pattern is 100 %. It is illustrated that the method is effective for fault diagnosis of rolling bearings.

Fig. 4RCMDE value of training sample

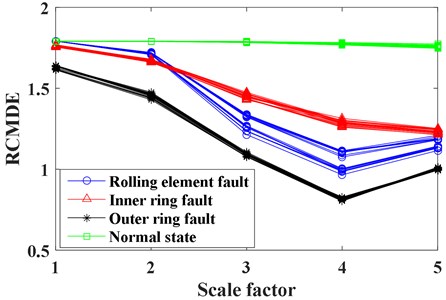
Fig. 5Diagnosis result of proposed method

In order to further prove that the performance of the proposed method is better than other methods, two hybrid method, multiscale fuzzy entropy (MFE) and multiscale sample entropy (MSE) combined with ISVM, are compared with the proposed method. At the same time, the combination of RCMFE and artificial neural network (ANN) is compared with the proposed method. The fault diagnosis recognition rate of the proposed method, MSE-ISVM, MFE-ISVM and RCMDE-ANN are shown in the Table 2. As shown in the Table 2, the recognition rate of the proposed method is higher than that of other methods, which proves the effectiveness of the proposed method.

Table 2The recognition rate of different classification methods

Method	Number of correct identification samples	Number of test samples	Recognition rate
RCMDE-ISVM	96	96	100 %
MSE-ISVM	93	96	96.88 %
MFE-ISVM	95	96	98.96 %
RCMDE-ANN	95	96	98.96 %

5. Case study 2

In order to further prove the effectiveness of the proposed method, the proposed method is used to diagnose the bearing fault dataset provided by Society for Machinery Failure Prevention Technology (MFPT). The bearings used in the case are NICE bearings. The bearing fault data set contains the following states: baseline (good condition bearing), inner race fault and outer race fault with various loads. The location of outer race fault and inner race fault of the bearing are shown in the Fig. 6. The data of each failure state are divided into 84 samples, a total of 256 samples, half of which are training samples and the other half are test samples.

Fig. 6Fault bearing: a) inner race fault, b) outer race fault

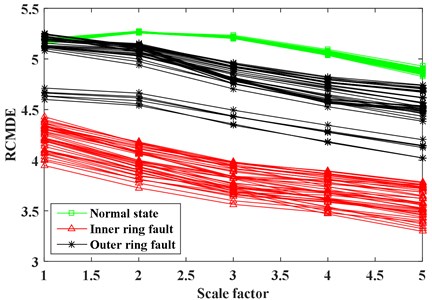
The parameter settings of RCMDE are consistent with the previous case. After calculation, the RCMDE value of the training sample is shown in the Fig. 7. As shown in the Fig. 7, the RCMDE values of different fault state can be distinguished clearly under different scale factor, which shows that the RCMDE as a characteristic parameter can reflect the fault state of bearings.

Fig. 7RCMDE value of training sample

The RCMDE is extracted to form feature vector as input of ISVM. Then the training samples are used to train the ISVM to obtain the optimal ISVM classification model. The parameter settings of WOA are the same as in the previous case. The diagnosis result is presented in the Fig. 8. As shown in the Fig. 8, the fault diagnosis results are in good agreement with the actual state. After calculated, the recognition accuracy of bearing fault pattern is 100 %. It is illustrated that the method is effective for fault diagnosis of rolling bearings.

In order to further prove that the performance of the proposed method is better than other methods. As in Case 1, MSE-ISVM, MFE-ISVM and RCMDE-ANN are used to compared with the proposed method. The fault diagnosis recognition rate of the proposed method, MSE-ISVM, MFE-ISVM and RCMDE-ANN are shown in the Table 3. As shown in the Table 3, the recognition rate of the proposed method is higher than that of MSE-ISVM and MFE-ISVM, which proves the effectiveness of the proposed method. The fault recognition rate of RCMDE-ANN is the same as that of the proposed method. The reason may be that RCMDE is so good at representing fault features that the classification of classifiers has little effect on fault recognition rate.

Fig. 8Diagnosis result of proposed method

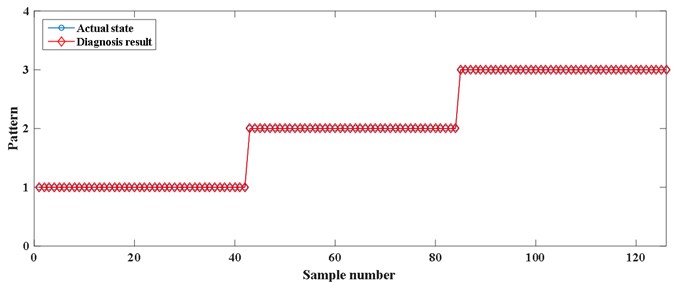
Table 3The recognition rate of different classification methods

Method	Number of correct identification samples	Number of test samples	Recognition rate
RCMDE-ISVM	126	126	100 %
MSE-ISVM	123	126	97.62 %
MFE-ISVM	124	126	98.41 %
RCMDE-ANN	118	126	100 %

6. Conclusions

In this paper, a novel method based on RCMDE and ISVM is presented for fault detection of rolling bearings. Due to RCMDE has the advantages of low computational cost and stable results, RCMDE is employed as the feature parameter to reflect the fault state of rolling bearings in this paper. The ISVM is proposed as a classifier for fault detection of rolling bearings, which has the advantages of less training samples and good classification performance. The experiment data from Case Western Reserve University and MFPT are used to verify the effectiveness of the proposed method. The experimental results show that the proposed method is effective in bearing fault diagnosis.

References

Gelman L., Murray B., Patel T. H., Thomson A. Vibration diagnostics of rolling bearings by novel nonlinear non-stationary wavelet bicoherence technology. Engineering Structures, Vol. 80, Issue 1, 2014, p. 514-520.

Publisher
Wang T., Liang M., Li J., Cheng W. Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis. Mechanical Systems and Signal Processing, Vol. 45, Issue 1, 2014, p. 139-153.

Publisher
Peng Z., Kessissoglou N. An integrated approach to fault diagnosis of machinery using wear debris and vibration analysis. Wear, Vol. 255, Issues 7-12, 2003, p. 1221-1232.

Publisher
Loutas T. H., Roulias D., Pauly E., Kostopoulos V. The combined use of vibration, acoustic emission and oil debris on-line monitoring towards a more effective condition monitoring of rotating machinery. Mechanical Systems and Signal Processing, Vol. 25, Issue 4, 2011, p. 1339-1352.

Publisher
Janssens O., Schulz R., Slavkovikj V., et al. Thermal image based fault diagnosis for rotating machinery. Infrared Physics and Technology, Vol. 73, 2015, p. 78-87.

Publisher
Ali Younus M. D., Yang Bo-Suk Intelligent fault diagnosis of rotating machinery using infrared thermal image. Expert Systems with Applications, Vol. 39, Issue 2, 2012, p. 2082-2091.

Publisher
Tran Van Tung, Yang Bo-Suk, Gu Fengshou, Ball Andrew Thernal image enhancement using bi-dimensional empirical mode decomposition in combination with relevance vector machine for rotating machinery fault diagnosis. Mechanical Systems and Signal Processing, Vol. 38, Issue 2, 2013, p. 601-614.

Publisher
Jena D. P., Panigrahi S. N. Automatic gear and bearing fault localization using vibration and acoustic signals. Applied Acoustics, Vol. 98, 2015, p. 20-33.

Publisher
Tandon N., Choudhury A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribology International, Vol. 32, Issue 8, 1999, p. 469-480.

Publisher
Glowacz A., Glowacz W., Glowacz Z., Kozik J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement, Vol. 113, 2018, p. 1-9.

Publisher
Dron J. P., Rasolofondraibe L., Bolaers F., Pavan A. High-resolution methods in vibratory analysis: application to ball bearing monitoring and production machine. International Journal of Solids and Structures, Vol. 38, Issues 24-25, 2001, p. 4293-4313.

Publisher
Altmann J., Mathew J. Multiple band-pass autoregressive demodulation for rolling element bearing fault diagnosis. Mechanical Systems and Signal Processing, Vol. 15, Issue 5, 2001, p. 963-977.

Publisher
Antoni J. The spectral kurtosis: a useful tool for characterising non-stationary signals. Mechanical Systems and Signal Processing, Vol. 20, Issue 2, 2006, p. 282-307.

Publisher
Antoni J., Randall R. B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines. Mechanical Systems and Signal Processing, Vol. 20, Issue 2, 2006, p. 308-331.

Publisher
Wang Y., Liang M. An adaptive SK technique and its application for fault detection of rolling element bearings. Mechanical Systems and Signal Processing, Vol. 25, Issue 5, 2011, p. 1750-1764.

Publisher
Wang D., Tse P. W., Tsui K. L. An enhanced kurtogram method for fault diagnosis of rolling element bearing. Mechanical Systems and Signal Processing, Vol. 35, Issues 1-2, 2013, p. 176-199.

Publisher
Jaskaran Singh, Darpe A. K., Singh S. P. Rolling element bearing fault diagnosis based on over-complete rational dilation wavelet transform and auto-correlation of analytic energy operator. Mechanical Systems and Signal Processing, Vol. 100, 2018, p. 662-693.

Publisher
Wang D., Zhao Y., Yi C., Tsui K., Lin J. Sparsity guided empirical wavelet transform for fault diagnosis of rolling element bearings. Mechanical Systems and Signal Processing, Vol. 101, Issue 15, 2018, p. 292-308.

Publisher
Guo Y., Liu T., Na J., Fung R. Envelope order tracking for fault detection in rolling element bearings. Journal of Sound and Vibration, Vol. 331, Issue 25, 2012, p. 5644-5654.

Publisher
Wang T., Liang M., Li J., Cheng, Li C. Bearing fault diagnosis under unknown variable speed via gear noise cancellation and rotational order sideband identification. Mechanical Systems and Signal Processing, Vol. 62, Issue 63, 2015, p. 30-53.

Publisher
Guo W., Tse P. W., Djordjevich A. Faulty bearing signal recovery from large noise using a hybrid method based on spectral kurtosis and ensemble empirical mode decomposition. Measurement, Vol. 45, Issue 5, 2012, p. 1308-1322.

Publisher
Xue X., Zhou J., Xu Y., Zhu W., Li C. An adaptively fast ensemble empirical mode decomposition method and its applications to rolling element bearing fault diagnosis. Mechanical Systems and Signal Processing, Vol. 62, Issue 63, 2015, p. 444-459.

Publisher
Azami H., Fernandez A., Escudero J. Refined multiscale fuzzy entropy based on standard deviation for biomedical signal analysis. Medical and Biological Engineering and Computing, Vol. 55, Issue 11, 2017, p. 2037-2052.

Publisher
Zhang L., Xiong G., Liu H., Zou H., Guo W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Systems with Applications, Vol. 37, Issue 8, 2010, p. 6077-6085.

Publisher
Zheng J., Cheng J., Yang Y., Luo S. A rolling bearing fault diagnosis method based on multi-scale fuzzy entropy and variable predictive model-based class discrimination. Mechanism and Machine Theory, Vol. 78, 2014, p. 187-200.

Publisher
Mirjalili S., Lewis A. The whale optimization algorithm. Advances in Engineering Software, Vol. 95, 2016, p. 51-67.

Publisher

Cited by

A rolling bearing fault diagnosis method based on vibro-acoustic data fusion and fast Fourier transform (FFT)

Xiao Fang | Jianbo Zheng | Bin Jiang

(2024)

Refined Composite Multiscale Phase Rényi Dispersion Entropy for Complexity Measure

Yu-Han Tong | Guang Ling | Zhi-Hong Guan | Qingju Fan | Li Wan

(2023)

Refined Composite Multiscale Fuzzy Dispersion Entropy and Its Applications to Bearing Fault Diagnosis

Mostafa Rostaghi | Mohammad Mahdi Khatibi | Mohammad Reza Ashory | Hamed Azami

(2023)

2023 IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC)

Yaxin Chen | An Zhu | Qisheng Zhao

(2023)

An ISVM Algorithm Based on High-Dimensional Distance and Forgetting Characteristics

Wenhao Xie | Jinfeng Li | Juanni Li | Xiaoyan Wang | Jiangbo Qian

(2022)

A novel wind turbine fault diagnosis method based on compressed sensing and DTL-CNN

Yan Zhang | Wenyi Liu | Xin Wang | Heng Gu

(2022)

A Novel Bearing Faults Detection Method Using Generalized Gaussian Distribution Refined Composite Multiscale Dispersion Entropy

Ragavesh Dhandapani | Imene Mitiche | Scott McMeekin | Gordon Morison

(2022)

Bearing Fault Diagnosis Method Based on RCMFDE-SPLR and Ocean Predator Algorithm Optimizing Support Vector Machine

(2022)

Bearing failure of reciprocating compressor sub-health recognition based on CAGOA-VMD and GRCMDE

Meiping Song | Jindong Wang | Haiyang Zhao | Yanyang Li

(2022)

A Method for Constructing Automatic Rolling Bearing Fault Identification Model Based on Refined Composite Multi-Scale Dispersion Entropy

Qingfeng Wang | Yang Xiao | Shuai Wang | Wencai Liu | Xiaojin Liu

(2021)

2021 International Conference on Electrical, Computer and Energy Technologies (ICECET)

Wulin Zhang | Jie Gao | Zeyu Liang | Zirui Liu

(2021)

Bearing Fault Diagnosis Using Refined Composite Generalized Multiscale Dispersion Entropy-Based Skewness and Variance and Multiclass FCM-ANFIS

Mostafa Rostaghi | Mohammad Mahdi Khatibi | Mohammad Reza Ashory | Hamed Azami

(2021)

About this article

Received

16 May 2019

Accepted

01 October 2019

Published

31 December 2019

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2019.20815

Keywords

rolling bearing

fault diagnosis

RCMDE

ISVM

WOA

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 01 21

Rolling bearing fault diagnosis based on variational mode decomposition and weighted multidimensional feature entropy fusion

Na Lei, Feihu Huang, Chunhui Li

Research article

2023 10 09

Extraction and diagnosis of rolling bearing fault signals based on improved wavelet transform

Zhiqing Cheng

Research article

2023 08 18

Fault diagnosis of rolling bearing based on cross-domain divergence alignment and intra-domain distribution alienation

Shubiao Zhao, Guangbin Wang, Xuejun Li, Jinhua Chen, Lingli Jiang

Research article

2023 08 01

A fault diagnosis method based on dilated convolution and attention for rolling bearing under multiple working conditions and noisy environments

Hui Zhang, Shengdong Liu, Ziwei Lv, Zhenlong Sang, Fangning Li

X. Zhang, J. Zhao, H. Teng, and G. Liu, “A novel faults detection method for rolling bearing based on RCMDE and ISVM,” Journal of Vibroengineering, Vol. 21, No. 8, pp. 2148–2158, Dec. 2019, https://doi.org/10.21595/jve.2019.20815

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2019.20815
UR  - https://doi.org/10.21595/jve.2019.20815
TI  - A novel faults detection method for rolling bearing based on RCMDE and ISVM
T2  - Journal of Vibroengineering
AU  - Zhang, Xin
AU  - Zhao, Jianmin
AU  - Teng, Hongzhi
AU  - Liu, Guozeng
PY  - 2019
DA  - 2019/12/31
PB  - JVE International Ltd.
SP  - 2148-2158
IS  - 8
VL  - 21
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhang_2019,
	doi = {10.21595/jve.2019.20815},
	url = {https://doi.org/10.21595/jve.2019.20815},
	year = 2019,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	number = {8},
	pages = {2148--2158},
	author = {Xin Zhang and Jianmin Zhao and Hongzhi Teng and Guozeng Liu},
	title = {A novel faults detection method for rolling bearing based on {RCMDE} and {ISVM}},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]X. Zhang, J. Zhao, H. Teng, and G. Liu, “A novel faults detection method for rolling bearing based on RCMDE and ISVM,” Journal of Vibroengineering, vol. 21, no. 8, pp. 2148–2158, Dec. 2019, doi: 10.21595/jve.2019.20815.

Copy IEEE

Copied to clipboard!

Zhang, Xin, Jianmin Zhao, Hongzhi Teng, and Guozeng Liu. “A Novel Faults Detection Method for Rolling Bearing Based on RCMDE and ISVM.” Journal of Vibroengineering 21, no. 8 (December 31, 2019): 2148–58. https://doi.org/10.21595/jve.2019.20815.

Copy Chicago

Copied to clipboard!

A novel faults detection method for rolling bearing based on RCMDE and ISVM

Abstract

Highlights

1. Introduction

2. Refined composite multiscale dispersion entropy

2.1. Multiscale dispersion entropy

2.2. Refined composite multiscale dispersion entropy

3. The improved support vector machine based on whale optimization algorithm

4. Case study 1

5. Case study 2

6. Conclusions

References

Cited by

About this article

Related Articles