Analysis of oscillations in discontinuous Lurie systems via LPRS method

1. Introduction

The necessity of studying stability and limiting dynamical regimes (attractors) arises in classical theoretical and applied problems. In [1] the classification of oscillations as being hidden or self-excited was proposed: self-excited oscillations can be visualized numerically by a trajectory starting from a point in a neighborhood of unstable equilibrium. In contrast, the basin of attraction for a hidden oscillation is not connected with equilibria and, it is necessary to develop special analytical and numerical methods to find initial points for their visualization. For nonlinear systems with a unique equilibrium and bounded solutions, the question that arises is how to find a class of systems for which the condition of the impossibility of generation of self-excited oscillations implies the absence of hidden oscillations.

Among engineers, one of the most widely used methods for searching and analyzing oscillations in nonlinear control systems is the harmonic balance method. It was developed in the 1920-1930s in the works of van der Pol [2] and Krylov and Bogolyubov [3] and later developed in the works of their followers (see [4-6]). It is known [1] that the harmonic balance method is an approximate method for determining the frequency and amplitude of periodic solutions. Moreover, the harmonic balance method may not predict hidden periodic oscillations [1].

The latter is true for the locus of a perturbed relay systems approach (LPRS method), that was developed in [7, 8] for Lurie systems with relay nonlinearities, despite the fact that the LPRS method makes it possible in many cases to predict oscillations not discoverable by the harmonic balance method.

In this article, using the example of known dynamical system with coexisting self-excited periodic oscillations, we will show that these methods may not reveal self-excited oscillations.

2. Oscillations in relay systems

Consider the following system with one scalar relay nonlinearity in the Lurie form:

where $\mathbf{x}\in {\mathbb{R}}^n$ is a state vector, $\sigma \in {\mathbb{R}}^1$, $\mathbf{A}\in {\mathbb{R}}^{n\times n}$, $\mathbf{B}\in {\mathbb{R}}^{n\times 1}$, $\mathbf{C}\in {\mathbb{R}}^{1\times n}$ are matrices, all quantities are real. We consider the solution of system Eq. (1) in the Filippov sense [9].

3. Example: Atherton’s system

Consider a relay control system in Lurie form, introduced by D. Atherton in [12], with the following matrices:

where $d$ is a parameter.

The linear part of system Eq. (7) is defined by the transfer function:

and the stationary set is as follows:

From Eq. (2) we get value of ${\omega }_0$:

and from:

we get $k=2d^2-4d+20.$

Next, from Eq. (4) we get value of amplitude $a$:

For the value $d=$ 1.2 we find frequency${\omega }_{hb}$ of a periodic solution as 2.75681. Now using formula Eq. (5) we build LPRS for system Eq. (7) (see Fig. 1).

Fig. 1The LPRS for system Eq. (7) for d = 1.2 and ω∈ [0.5, 10]

Solving equation Eq. (6) using MATLAB function “vpasolve()” with a given tolerance 10^-8, we find frequency of periodic solution as ${\omega }_{LPRS}=$ 2.739991399. Initial data this periodic solution is given in Table 1.

We can examine orbital stability of the oscillations using the following approach proposed in [13] and generalized for the linear parts containing delays and integrators in [8]. It is formulated as the following theorem:

Theorem 1. Periodic motions in system Eq. (1) are locally orbitally asymptotically stable if and only if all eigenvalues of the matrix:

where $T=2\pi /\omega$ is the period of the oscillations, $\mathbf{v}$ is the value of the velocity matrix at the time of the relay switch, in the periodic motion, $\mathbf{v}\left(\frac{T}{2}-0\right)=2{\left(\mathbf{I}+e^{\mathbf{A}\frac{T}{2}}\right)}^{-1}{e}^{\mathbf{A}\frac{T}{2}}\mathbf{B}$, have magnitudes less than one.

For system Eq. (7) the corresponding eigenvalues are ${\lambda }_1=$ 1.457, ${\lambda }_2=$ 0.279, ${\lambda }_3=$ 0. Since one of eigenvalues has magnitude greater than 1, the motion is not orbitally stable. Therefore, a symmetric periodic solution exists but it is orbitally unstable and cannot reveal itself as an oscillation.

3.1. Numerical modeling

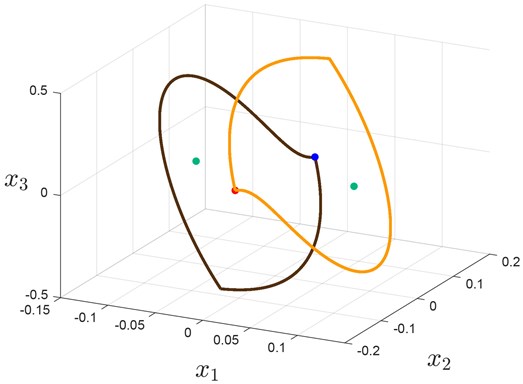
Using special computational package [14] and initial data from Table 2 we can visualize two self-excited (with respect to rest segment) asymmetric periodic solutions (see Fig. 2), that cannot be found using harmonic balance method and LPRS method.

Table 1Parameters of two asymmetric solutions of system Eq. (7)

$\omega$	2.608029064355592
$T$	2.409169971705080
$\lambda$	0.296489410929823

Table 2Initial data of two asymmetric solutions of system Eq. (7)

$x_1$	$\pm$0.000000000312706
$x_2$	$\mp$0.110095383325227
$x_3$	$\pm$0.037742341170832

Fig. 2Trajectories with initial data from Table 3

4. Conclusions

In this paper it is shown that the harmonic balance method and the LPRS method may not predict the existence of all self-excited oscillations. A symmetric periodic solution exists but it is orbitally unstable and cannot reveal itself as an oscillation. Although the LPRS does not detect hidden and self-excited asymmetric oscillations, it would be possible to develop a certain extension to the LPRS method to solve these problems.