Aero-hydrodynamic loads investigations for different constructions in turbulent flows with special verification approach

1. Introduction

This work is step forward to creation and application of mathematical models for the most dangerous oscillations excitation mechanisms for different constructions in liquid or air flow, as well as to creation of efficient computational methods for description of these models and processes. The paper contains some results of analysis for numerical modeling data, exact as it possible to determine aerodynamic loads in all these cases with constructions and objects of transport (Fig. 1). It includes definition of pressure and flow velocities distributions on the surfaces of specified objects and also with special investigation of amplitude-frequency characteristics for the individual construction elements. According to proposed special verification methodical approach [1-3] authors confirmed efficiency and correctness of the obtained results. This includes too the application of the main original combined numerical approach as for calculation process so as for effective verification of obtained results with support of special analysis.

Fig. 1Application of the proposed approach in railway transport systems (the pedestrian bridge)

Numerical investigation method of hydrodynamic forces arising from separated flow, and construction oscillations excited by these forces, were worked out by authors. For this task decision authors proposed numerical methodic (Fig. 2) of aero-hydrodynamic loads modeling from high-speed trains (ANSYS-CFX) –2D-3D task decisions in combination with some specially chosen vortices methods, such as elaborated in Institute for Machine Science of the Russian Academy of Sciences Modernized Method of Discrete Vortices (MMDV) – for decision of 2D – tasks especially in this direction [4, 5].

Fig. 2The Scheme of proposed combined approach functioning for complicated systems decision (elaborated by authors [2, 5])

2. Numerical methodic of aero-hydrodynamic loads modeling

2.2. Modernized method of discrete vortices (MMDV) – for decision of 2D – problems [3]

Method does not require grids construction and does not contain empirical parameters.

The numerical scheme is stable (there are no stops due to unlimited growth of variables number).

The developed method significantly extends possibilities of vortex formation mechanism numerical study at arbitrary motion and streamlined bodies shape changing

Existing software systems of computational fluid dynamics with grid methods are sometimes ineffective, because calculation of variable geometry structures is extremely long.

On a single mathematical and computational basis it is possible to create software hierarchy system which covers a wide range of applications. According to this basis with account of physical experiment applicability limits these schemes and models are realized successfully. Method is characterized by unique ability of vortex traces and flow formation at the same time. The dimension of problem is significantly reduced, since it is necessary to monitor not the entire area, but only vortices on the body surface and in the wake.

Apparently, it can be argued that the numerical experiment based on discrete vortices method has elements of what is commonly called “artificial intelligence” as it reproduces those features of process which were not explicitly incorporated into algorithms and models.

Calculation example with ANSYS – CFX (3D) and MMDV (2D) with application for pressure distribution definition on the surface of the pedestrian bridge and by according measuring and verification (Figs. 3-5).

Fig. 3The pedestrian bridge

Direct calculations of flow velocity from high speed train aerodynamic effects were worked out in 3D by means of software module ANSYS (CFX), which allows on the base of Navies-Stocks equations to receive decision in form of dependence of flow velocity on the bridge from the distance between train and pedestrian bridge (all the surfaces of bridge). After that it is necessary to value magnitudes of flow velocity components near the bridge as $V_1$ – velocity in horizontal plane perpendicularly to bridge, $V_2$ – velocity in horizontal plane along the bridge and V₃ velocity in vertical plane perpendicularly to horizontal plane.

In this case it is necessary to choose the main air flow with velocity V₁ in horizontal plane perpendicularly to bridge in the direction to the bridge with corresponding values of velocity for 2D realization of task decision with MMDV application. Main results in this case of plain 2D task are in Fig. 5. Shown in Fig. 5 coefficients $C_x$ and $C_y$ give the opportunity to define dependencies of aerodynamic forces from time.

Fig. 4Calculation of pressure on pedestrian bridge surface

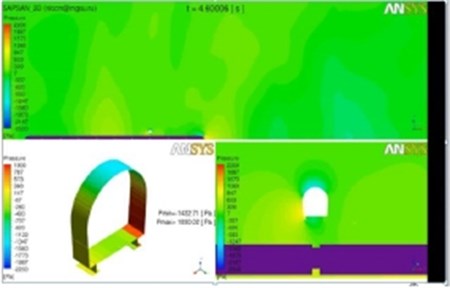
Fig. 5The estimated Karman vortices paths and aerodynamic forces for the pedestrian bridge

3. Concluding remarks

It is necessary also to remark, that MMDV Method allows to research aerodynamic loads on bodies making arbitrary movements and to solve problems of body motion under aerodynamic forces.

The calculation was carried out using both statements (verification of relative differences are not more than 10-15 %) for the pedestrian bridge [3, 5, 7, 8], shown in Fig. 3-5.

Initial values of the approach flow velocity are obtained from the solution of problem in ANSYS CFX in 3D setting (its initial stage) (Fig. 2) in accordance with the scheme of methods interaction in combined approach framework. In a 3D setting, furthermore, pressure distributions on the bridge structure during the passage of a high-speed train under the pedestrian bridge are obtained (Fig. 3, 4) with pressure magnitudes from 200 till 1120 Pa ($p_{min}=$160 Pa and $p_{max}=$ 1120 Pa) as well as according dependences of lifting and drag forces from time and frequency characteristics of the flow loading process (Fig. 5).

The paper is devoted to the analysis and verification of numerical modeling data in determining of aero-hydrodynamic loads or vibrations and impacts from dynamic problems typical for high-speed trains influence on standard infrastructure facilities of JSC “Russian Railways”, such as pedestrian bridges, wall screens and tunnels.

The purpose of this work is the analysis of data obtained by calculation of the frequency spectra components of the aero-hydrodynamic loads, pressure and speed or velocity distributions on the specified objects and amplitude-frequency characteristics for the individual construction elements.

It confirms efficiency and correctness of the results obtained by authors with the application attached to proposed original combined calculation approach. This approach is a linked system of carrying out complex research by two advanced calculation methods in their permanent interaction with an increased efficiency and with significant reduction in the cost (on 20-30 %) of expenditures realization for numerical investigations.

The obtained data were verified according to proposed scheme of interaction with the use of the bank of experimental data collected by authors, including test data at both the international standard models and the domestic ones (tests with liquid and air flows in wind tunnels and on aero-hydrodynamic stands). Relative error of such approach for the whole raw of decided tasks is about 10-17 %.