Dynamics similarity design and verification of rotor system

1. Introduction

In terms of rotor dynamics test and dynamic similarity, many scholars have carried out a lot of useful explorations and achieved many results. Guoqiang H aimed at the simulation of the torsional vibration frequency of the rotor system, and used the physical structure similarity principle to design an analog rotor system similar to the physical structure of the 600 MW steam turbine shafting, The simulated rotor can better simulate the dynamic characteristics of the original steam turbine shaft [1]. Paul designed a rotor tester for rotor dynamics research based on similarity theory [2]. Guozhi Chen established a simulated rotor to simulate the dynamic characteristics of a gas generator rotor [3]. Wu had analyzed the dynamic similarity of the scale model rotor and the actual rotor system based on the similarity theory. Which showed that the frequency of the scale model is proportional to the actual rotor, and the scale model can be used to predict vibration characteristics to the actual rotor [4]. Zhongyong Gao applied the similarity theory to the design of the rotor tester. A simple rotor test model design method was proposed after the similarity of the model rotor and the actual rotor is discussed by the Ranlin’s formula and the matrix iteration formula [5]. Luo had put forward the similar condition of model rotor and actual rotor after researched equation analysis method and dimensional analysis method [6].

The similarity criteria of the normal model and the original model for the rotor system is obtained by the dimensional analysis method in this paper. The critical speeds of the normal model and the original model were calculated by the finite element software ANSYS, and the similarity is verified.

2. Dimensional method

According to the structural characteristics of the rotor system and its differential equation of motion, the relevant physical quantities of the rotor model include: excitation force $F$, excitation frequency ${\omega }_0$, geometry size $l$, time $t$, elastic modulus $E$, stress $\sigma$, strain $s$, Poisson ratio $\mu$, damping ratio $\xi$, material density $\rho$, displacement response $U$, critical speeds $f$, bearing stiffness coefficient $k$ and bearing damping coefficient $c$.

For the normal vibration operation of the rotor, the relationship of the physical quantities of the rotor system in the linear elastic range can be expressed as:

According to the$\mathrm{}\pi$- principle, $\pi$ criteria can be derived as follows:

In the similar model design of the rotor system, all physical quantities of the normal model and the original model must be proportional. The normal model and the original model are respectively represented by subscripts $m$ and $p$. It is assumed that geometrical dimensions $l_m$ and $l_p$ satisfy the similarity ratio $C_l$, the times $t_m$ and $t_p$ satisfy the similarity ratio $C_t$, the densities ${\rho }_m$ and ${\rho }_p$ satisfy the similarity ratio $C_{\rho }$, the elasticity modulus $E_m$ and $E_p$ satisfy the similarity ratio $C_E$, the excitation frequencies ${\omega }_{0_m}$ and ${\omega }_{0_p}$ satisfy the similarity ratio $C_{{\omega }_0}$, the excitation forces $F_m$ and $F_p$ satisfy the similarity ratio $C_F$, the displacement responses $U_m$ and $U_p$ satisfy the similarity ratio $C_U$, the velocity responses $V_m$ and $V_p$ satisfy the similarity ratio $C_v$, the acceleration responses $a_m$ and $a_p$ satisfy the similarity ratio $C_a$, and the support stiffness coefficients $k_m$ and $k_p$ satisfy the similarity ratio $C_k$, the bearing damping coefficients $c_m$ and $c_p$ satisfy the similarity ratio $C_c$, the scale formula can be obtained.

According to the scaling formula, the dynamic similarity of the normal model and the original model can be written as [7]:

If the $r$-order mode of normal model and original model are ${\left\{{\psi }_r\right\}}_m$ and ${\left\{{\psi }_r\right\}}_p$ respectively, then ${\left\{{\psi }_{ir}\right\}}_m/{\left\{{\psi }_{ir}\right\}}_p=C_l$. It can be seen that when the model size is fixed, there is a direct proportion of ${\left\{{\psi }_r\right\}}_m$ and ${\left\{{\psi }_r\right\}}_p$, and the modal shape is the complex amplitude ratio of each measurement point, substantially. If the modal shapes of two models are standardized on the elements in the same position, then:

The modal shapes are exactly the same for the normal model and the original model in the same order.

In rotor model design, the normal model and original model are generally made of the same material, then $C_E=C_{\rho }=$1. If the geometric scale is $C_l=\lambda$, then the physical quantities of normal model and the original model are shown in Table 1.

3. Establishment of normal model of rotor system

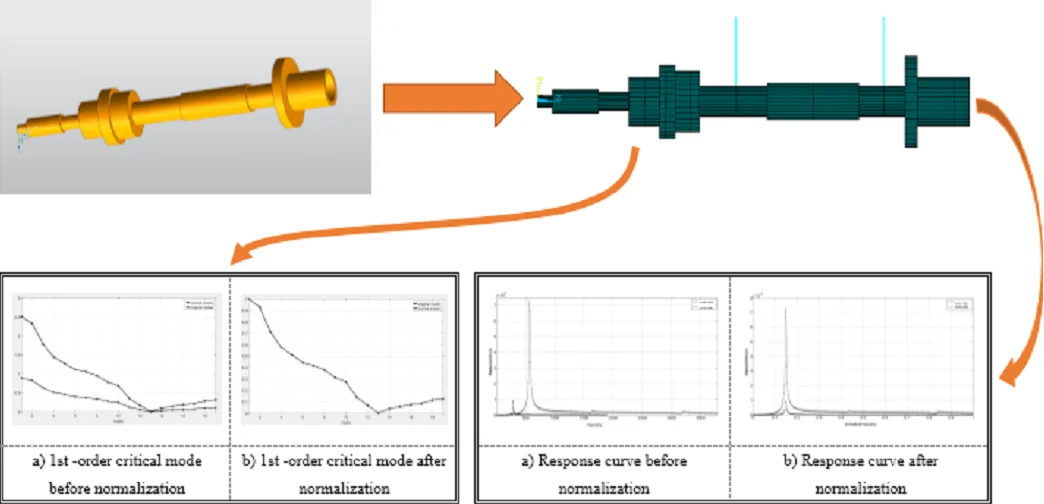
As can be seen from Fig. 1. the original model consists of a rotating shaft and a disk, and two bearings with elasticity. Basic data of the original model is shown in Table 2. The finite element model of the rotor system is established according to the geometric model of the rotor system, as shown in Fig. 2. The rotating shaft is simulated by BEAM188, the disk is simulated by MASS21, and the bearing is simulated by COMBI214.

Fig. 1Structure of rotor system of original model

Fig. 2Finite element model of the rotor system

In order to analyze the dynamic similarity between the normal model and original model, according to the similarity criteria, the normal model is established. All the relevant parameters shown in Table 3 are strictly in accordance with the similarity relation for the similarity transformation.

4. Similarity analysis of dynamic characteristics of normal model and original model

The finite element models of the normal model and the original model are established respectively, and the modal analysis is carried out by QR method. The critical speeds of the normal model and the original model can be obtained with simulation analysis that has been shown in Table 4.

Table 4 and 5 show that the critical speeds of normal model are twice as much as that of the original model and the strain energy distribution is exactly the same.

The modal shapes of the normal model of the rotor system can be obtained by using ANSYS. At the same time, the modal displacements of each order can be extracted and normalized. The modal displacement diagram of each node is shown in Fig. 3.

Fig. 3Comparison and the first three critical modes of the original model and the normal model

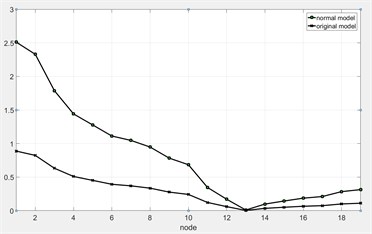
a) 1st -order critical mode before normalization

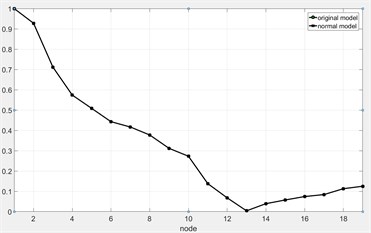
b) 1st -order critical mode after normalization

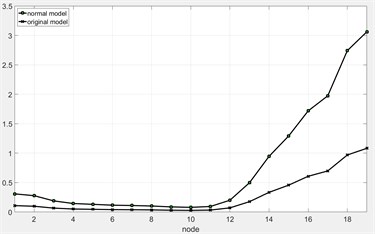
c) 2nd -order critical mode before normalization

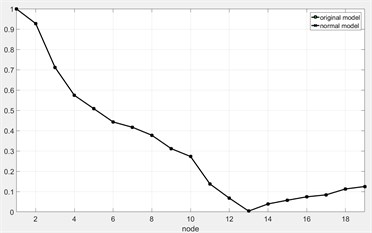
d) 2nd -order critical mode after normalization

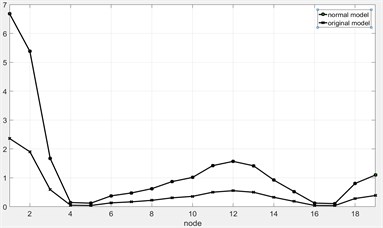
e) 3rd -order critical mode before normalization

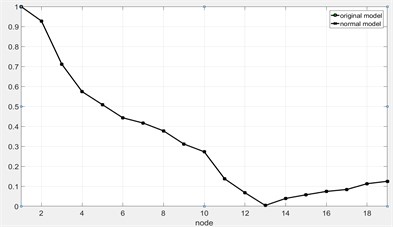
f) 3rd -order critical mode after normalization

With the similarity analysis of the normal model and the original model for the rotor system, it can be found that dynamic characteristics of the normal model for the rotor system is similar to the dynamic characteristics of the original model. Therefore, the modal shapes and the critical speeds of the original model for the rotor system can be accurately predicted by the normal model.

In order to compare and analyze the similarity of the dynamic response for the normal model and the original model, the harmonic response analysis is carried out. With the harmonic response analysis, the steady-state response of the complex structure under the harmonic load can be determined. The damping effect need to be considered when studying the forced vibration response characteristics of the rotor. If the original model damping is 5 N/(m/s), and then the normal model damping is 25 N/(m/s) according to the similarity ratio.

The modal superposition method is used to analysis rotor harmonic response. The exciting forces applied to the normal model and the original model are 2.5 N and 10 N, respectively. With harmonic response analysis, the steady state response of each rotor system at the disk is obtained. The frequency response curves are shown in Fig. 4 and Fig. 5.

Fig. 4The frequency response curve of the normal model and the original model at the disk

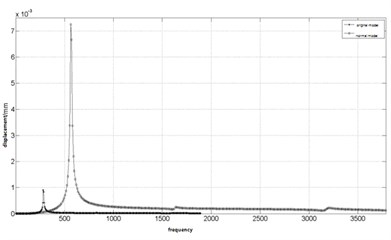
a) Response curve before normalization

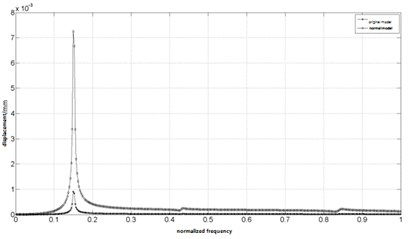
b) Response curve after normalization

Fig. 5The frequency response curve of the normal model and the original model at the bearing

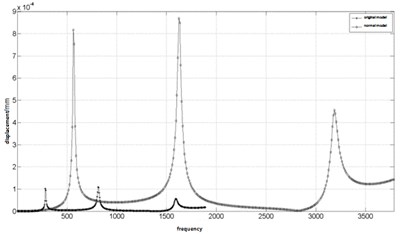
a) Response curve before normalization

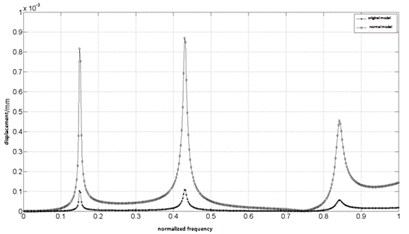
b) Response curve after normalization

Fig. 4 and Fig. 5 show that the displacement-frequency curve of the normal model is basically similar to the curve of original model. It can be seen that the frequency dynamic response of two models are similar, so the normal model can accurately predict the frequency response characteristics of the original model subjected to external loads.

5. Conclusions

The normal similarity theory of the rotor system dynamic model was discussed in this paper. Based on the dimensional analysis method, the similarity criteria of the normal and original models for the rotor system were derived and the dynamic similarity relationship of two models were established. the dynamic characteristics and dynamic response similarity were analyzed by numerical simulation. the main conclusions show that:

1) The critical speeds of the normal and original models for the rotor system satisfy the determined relationship. in other words, if the geometrical size of the model is scaled down to 1/$n$ times of the original model, the critical speeds of the normal model will increase to n times of the original model. In addition, the vibration modes and the dynamic characteristics of the two models are completely identical.

2) With the application of similarity criteria, the amplitudes of response curves of the normal model is consistent with the amplitudes of the original model. in addition, dynamic response of two models are similar. Therefore, the normal model can accurately predict the forced vibration response characteristics of the original model under external loads.

Therefore, the normal model can accurately predict the dynamic vibration characteristics of the original model rotor system such as modal shapes, critical speeds and harmonic response.