Evaluation of critical path of construction projects by using the new BWABAC method under uncertainty

Noshadpoor, Keivan

doi:10.21595/vp.2019.21125

Vibroengineering Procedia

Browse Procedia

Published: 07 May 2020

Check for updates

Evaluation of critical path of construction projects by using the new BWABAC method under uncertainty

Keivan Noshadpoor¹

¹Saman Sazan Bisotoun Engineering Group, Lamerd, Iran

Cite the article Download PDF

Downloads 1107

Abstract

The project’s scheduling and planning project is a crucial factor in achieving success. In order to better scheduling and planning, critical path method (CPM) is extended by adding some efficient criteria to the old CPM. In this paper, to determine the critical path of projects by useful criteria, a new MCDM method named BWABAC is proposed. For determining the weight of important criteria, the best-worst method (BWM) is applied. Furthermore, the multi-attributive border approximation area comparisons (MABAC) procedure is used to rank all paths of project network. Finally, the new MCDM method is extended under type-2 fuzzy sets (T2FSs) to tackle the uncertainty. T2FSs are much stronger tool than classic fuzzy sets because the membership grade of T2FSs is a classic fuzzy set. Moreover, the BWABAC method is compared with the COPRAS method to drown the validity. Eventually, an illustrative example is solved to display the strengths of BWABAC method.

Evaluation of critical path of construction projects by using the new BWABAC method under uncertainty

Highlights

Considering the superiorities of the best-worst approach (BWM) in contrast with the AHP approach, an extension of BWM approach is introduced under T2FSs for criteria weight determination.
The MABAC approach, as a well-known MCDM approach, is applied to rank of projects’ paths. Note that, the MABAC method is developed under IT2FSs For Facing with uncertainty.
A new approach, namely the BWABAC method is extended to critical path determination in construction projects.

1. Introduction

One of the most important issues in project management is planning and scheduling phase. Furthermore, one of the most commonly used methods for the scheduling is critical path method (CPM). In the past, critical path of project was determined only by time criterion [1]. Gradually, [2] modeled the critical path method as an MCDM method. [3] evaluated critical path of project by using time, cost, risk and quality criteria. They solved this problem by TOPSIS method. [4] solved the critical path problem by PROMETHEE method. He considered the time, cost, safety, and quality criteria. [5] proposed a new approach for evaluating the critical path under fuzzy environment. [6] selected the critical path of projects by a new MCDM method under intuitionistic fuzzy sets.

One of the approaches that have attracted great attention in last decade is multi-attributive border approximation area comparisons (MABAC) method. The MABAC originally proposed by [7]. The MABAC method has been applied in manifold areas, successfully. For instance, [8] evaluated hotels on a tourism website. [9] used the MABAC method for supplier selection of construction companies. [10] selected the best outsourcing provider by using the MABAC method. Some of the major advantages of MABAC approach are easy to use and permanence in solution and the possible quantity of gains and losses which to be defined such a procedure that the final outcome can be spacious. In MCDM methods, a stable and reliable procedure for determining the weight of criteria is very necessary.

The analytic hierarchy process (AHP) is the most commonly used method in various areas. AHP method is criticized for two reasons; Pairwise comparisons for a large number of criteria is a very lengthy procedure. Furthermore, the inconsistency among criteria is high in the big size problems. To overcome this shortage, the best worst method (BWM) has introduced by [11]. BWM method has been applied in many various areas [12-14]. In this paper, to use merits of BWM method and MABAC method, these two methods are applied, simultaneously. The name of new MCDM method is BWABAC method.

Furthermore, for tackling the derived uncertainty of projects’ nature and judgment of experts, fuzzy sets theory was originally introduced by [15]. For experts, assign a crisp membership to the classic fuzzy sets are difficult. That is why type-2 fuzzy sets (T2FSs) was proposed by [16]. The membership grade of T2FSs is a classic fuzzy set. With this in mind, T2FSs in comparison with classic fuzzy sets is much powerfull for addressing the uncertainty. T2FSs are successfully applied in manifold MCDM areas, recently. [17] extended a new approach for selecting the best robot under interval T2FSs (IT2FSs). [18] planned turkey energy by using an MCDM method under T2FSs. In this paper, the new BWABAC method is extended under IT2FSs to achieve reliable outcomes and determining the critical path.

Totally, to utilize superiorities of MABAC and BWM method, a new MCDM method named BWABAC is extended to critical path selection problem, properly. Moreover, to employ the suitability of IT2FSs, the BWABAC method is developed under IT2FSs to achieve reliable and stable outcomes about specifying the critical path of projects and consequently achieve better planning and scheduling. The novelties of the suggested approach in comparisons of the literature are drawn as follows: 1) In this paper, considering the superiorities of the best-worst approach (BWM) in contrast with the AHP approach, an extension of BWM approach is introduced under T2FSs for criteria weight determination. 2) The MABAC approach, as a well-known MCDM approach, is applied to rank of projects’ paths. Note that, the MABAC method is developed under IT2FSs For Facing with uncertainty. 3) Finally, a new approach, namely the BWABAC method is extended to critical path determination in construction projects.

The paper is configured as below: Section 2 represents the BWABAC method for specifying the critical path. Section 3 demonstrates an illustrative example. Section 4 compares the BWABAC method with the COPRAS method. Section 5 draws the conclusions.

2. Suggested method

BWM approach is extended for the weight determination of criteria. Then, the MABAC approach is developed for critical path selection. Finally, the proposed comprehensive method named BWABAC is extended by using type-2 fuzzy sets. Because of nature of projects, uncertainty plays an important role during the critical path selection procedure. That is why type-2 fuzzy sets are applied to cope with the uncertainty. The proposed method is explained by using the following steps:

Step 1: Construction decision matrix.

Step 1-1: In this sub-step, the information about cost, time, risk, quality, and safety criteria for each activity is collected from an expert. Information about qualitative criteria is explained by using linguistic variables that demonstrated in Table 1.

Step 1-2: Form the decision matrix by considering all path as alternatives and considering time ( $z_{1}$ ), cost ( $z_{2}$ ), risk ( $z_{3}$ ), quality ( $z_{4}$ ), and safety ( $z_{5}$ ) as efficient criteria by using the following:

1

χ = ({\tilde{\tilde{χ}}}_{i j}^{})_{p \times n} = \begin{matrix} \begin{array}{l} z_{1} & \dots & z_{n} \end{array} \\ \begin{array}{l} p a t h 1 \\ ⋮ \\ p a t h p \end{array} & (\begin{array}{l} {\tilde{\tilde{χ}}}_{11}^{} & \dots & {\tilde{\tilde{χ}}}_{1 n}^{} \\ ⋮ & ⋱ & ⋮ \\ {\tilde{\tilde{χ}}}_{p 1}^{} & \dots & {\tilde{\tilde{χ}}}_{p n}^{} \end{array}) \end{matrix}, i = 1, . . ., p, j = 1, . . ., n .

Step 2: The constructed decision matrix is normalized by:

2

η_{k} = ({\tilde{\tilde{η}}}_{i j}^{k})_{p \times n} = (\begin{array}{l} {\tilde{\tilde{η}}}_{11}^{k} & \dots & {\tilde{\tilde{η}}}_{1 n}^{k} \\ ⋮ & ⋱ & ⋮ \\ {\tilde{\tilde{η}}}_{p 1}^{k} & \dots & {\tilde{\tilde{η}}}_{p n}^{k} \end{array}) .

The normalized positive criteria are defined as below:

3

{\tilde{\tilde{η}}}_{i j} = [(\begin{array}{l} \frac{χ_{i j 1}^{U}}{χ^{+}}, \frac{χ_{i j 2}^{U}}{χ^{+}}, \frac{χ_{i j 3}^{U}}{χ^{+}}, \frac{χ_{i j 4}^{U}}{χ^{+}}; \\ H_{1} ({\tilde{χ}}_{}^{U}), H_{2} ({\tilde{χ}}_{}^{U}) \end{array}), (\begin{array}{l} \frac{χ_{i j 1}^{L}}{χ^{+}}, \frac{χ_{i j 2}^{L}}{χ^{+}}, \frac{χ_{i j 3}^{L}}{χ^{+}}, \frac{χ_{i j 4}^{L}}{χ^{+}}; \\ H_{1} ({\tilde{χ}}_{}^{L}), H_{2} ({\tilde{χ}}_{}^{L}) \end{array})] .

The normalized negative criteria are defined as follows:

4

{\tilde{\tilde{η}}}_{i j} = [(\begin{array}{l} \frac{χ^{-}}{χ_{i j 4}^{U}}, \frac{χ^{-}}{χ_{i j 3}^{U}}, \frac{χ^{-}}{χ_{i j 2}^{U}}, \frac{χ^{-}}{χ_{i j 1}^{U}}; \\ H_{1} ({\tilde{χ}}_{}^{U k}), H_{2} ({\tilde{χ}}_{}^{U k}) \end{array}), (\begin{array}{l} \frac{χ^{-}}{χ_{i j 4}^{L}}, \frac{χ^{-}}{χ_{i j 3}^{L}}, \frac{χ^{-}}{χ_{i j 2}^{L}}, \frac{χ^{-}}{χ_{i j 1}^{L}}; \\ H_{1} ({\tilde{χ}}_{}^{L k}), H_{2} ({\tilde{χ}}_{}^{L k}) \end{array})],

where, $χ^{+} = \underset{i}{m a x} \{χ_{i j 4}^{U k}\}$ , $χ^{-} = \underset{i}{m a x} \{χ_{i j 1}^{U k}\}$ .

Step 3: Specify the weight of criteria by using the BWM method.

Step 3-1: Define the best and worst criteria.

The most significant (best) and least significant (worst) criteria in terms of weight are determined.

Step 3-2: Express the priority of best criterion over the other criteria.

The priority of best criterion over the other criteria is collected from experts by means of the linguistic variables. The linguistic variables and their equivalent IT2FSs are illustrated in Table 2. The vector of best to over criteria is explained as follows:

5

{\tilde{\tilde{β}}}_{M C} = ({\tilde{\tilde{β}}}_{M C, 1}, {\tilde{\tilde{β}}}_{M C, 2}, . . ., {\tilde{\tilde{β}}}_{M C, n}) .

Table 1Equivalent IT2F of linguistic terms for ratings [19]

Linguistic terms	Interval type-2 fuzzy numbers
Very low (VL)	((0, 0, 0, 0.1; 1, 1), (0, 0, 0, 0.05; 0.9, 0.9))
Low (L)	((0, 0.1, 0.1, 0.3; 1, 1), (0.05, 0.1, 0.1, 0.2; 0.9, 0.9))
Medium low (ML)	((0.1, 0.3, 0.3, 0.5; 1, 1), (0.2, 0.3, 0.3, 0.4; 0.9, 0.9))
Medium (M)	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))
Medium high (MH)	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))
High (H)	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))
Very high (VH)	((0.9, 1, 1, 1; 1, 1), (0.95, 1, 1, 1; 0.9, 0.9))

Table 2Equivalent IT2F of linguistic terms for weightings of criteria [20]

Linguistic variables	Interval type-2 fuzzy scales
Absolutely strong (AS)	((7, 8, 9, 9; 1, 1), (7.2, 8.2, 8.8, 9; 0.9, 0.9))
Very strong (VS)	((5, 6, 8, 9; 1, 1), (5.2, 6.2, 7.8, 8.8; 0.9, 0.9))
Fairly strong (FS)	((3, 4, 6, 7; 1, 1), (3.2, 4.2, 5.8, 6.8; 0.9, 0.9))
Slightly strong (SS)	((1, 2, 4, 5; 1, 1), (1.2, 2.2, 3.8, 4.8; 0.9, 0.9))
Exactly equal (E)	((1, 1, 1, 1; 1, 1), (1, 1, 1, 1; 1, 1))

Step 3-3: Explain the priority of other criteria over the worst criterion.

The priority of other criteria over the worst criterion are collected from experts by using the linguistic variables that were demonstrated in Table 1. The vector of others to the worst criterion is defined as follows:

6

{\tilde{\tilde{β}}}_{L I} = ({\tilde{\tilde{β}}}_{L C, 1}, {\tilde{\tilde{β}}}_{L C, 2}, . . ., {\tilde{\tilde{β}}}_{L C, n}) .

Furthermore, the above vectors are defuzzified by:

7

D e f ({\tilde{\tilde{β}}}_{1}^{}) = \frac{1}{2} (\sum_{O \in \{U, L\}}^{} \frac{β_{11}^{O} + (1 + H_{1} ({\tilde{β}}_{1}^{O})) β_{12}^{O} + (1 + H_{2} ({\tilde{β}}_{1}^{O}) β_{13}^{O} + β_{14}^{O}}{4 + H_{1} ({\tilde{β}}_{1}^{O}) + H_{2} ({\tilde{β}}_{1}^{O})}) .

Step 3-4: Obtain the final and optimal weight of criteria.

The linear model is used to achieve unique weights of criteria as follows:

8

\begin{array}{l} m i n γ, \\ |δ_{M C} - β_{M C, j} * δ_{j}| \leq γ, for  all j, \\ |δ_{j} - β_{j, L C} * δ_{L C}| \leq γ, for  all j, \\ \sum_{j = 1}^{n} δ_{j}^{} = 1, δ_{j}^{} \geq 1, for  all j . \end{array}

Notably, $γ$ demonstrates consistency. The amount of close to zero shows high consistency. Furthermore, the optimal weight $(δ_{1}^{*}, δ_{2}^{*}, . . ., δ_{n}^{*})$ is obtained from above linear model.

Step 4: Create the weighted normalized decision matrix by means of:

9

{\tilde{\tilde{B}}}_{i j} = {({\tilde{\tilde{b}}}_{i j}^{})}_{m \times n} = {\tilde{\tilde{η}}}_{i j}^{} * δ_{j} .

Step 5: Calculate border approximation area vector by:

10

{\bar{\tilde{\tilde{ψ}}}}_{j} = [\begin{array}{l} {\bar{\tilde{\tilde{ψ}}}}_{1} & \dots & {\bar{\tilde{\tilde{ψ}}}}_{n} \end{array}] .

Each element is obtained via:

11

{\bar{\tilde{\tilde{ψ}}}}_{1} = (\begin{matrix} ({(\prod_{i = 1}^{p} b_{i j 1}^{U})}^{(\frac{1}{p})}, {(\prod_{i = 1}^{p} b_{i j 2}^{U})}^{(\frac{1}{p})}, {(\prod_{i = 1}^{p} b_{i j 3}^{U})}^{(\frac{1}{p})}, {(\prod_{i = 1}^{p} b_{i j 4}^{U})}^{(\frac{1}{p})}); \\ m i n (H_{1} ({\tilde{B}}_{11}^{U}), . . ., H_{1} ({\tilde{B}}_{L 1}^{U})), m i n (H_{2} ({\tilde{B}}_{11}^{U}), . . ., H_{2} ({\tilde{B}}_{L 1}^{U})) \\ ({(\prod_{i = 1}^{p} b_{i j 1}^{L})}^{(\frac{1}{p})}, {(\prod_{i = 1}^{p} b_{i j 2}^{L})}^{(\frac{1}{p})}, {(\prod_{i = 1}^{p} b_{i j 3}^{L})}^{(\frac{1}{p})}, {(\prod_{i = 1}^{p} b_{i j 4}^{L})}^{(\frac{1}{p})}); \\ m i n (H_{1} ({\tilde{B}}_{11}^{L}), . . ., H_{1} ({\tilde{B}}_{L 1}^{L})), m i n (H_{2} ({\tilde{B}}_{11}^{L}), . . ., H_{2} ({\tilde{B}}_{L 1}^{L})) \end{matrix}) .

Step 6: Compute the distance of alternatives from border approximation area:

12

{\tilde{\tilde{σ}}}_{i j} = {\tilde{\tilde{B}}}_{i j} - {\bar{\tilde{\tilde{ψ}}}}_{j} = (\begin{matrix} ({\tilde{\tilde{η}}}_{11}^{} * δ_{1}) - {\bar{\tilde{\tilde{ψ}}}}_{1} & \dots & ({\tilde{\tilde{η}}}_{1 n}^{} * δ_{n}) - {\bar{\tilde{\tilde{ψ}}}}_{n} \\ ⋮ & ⋱ & ⋮ \\ ({\tilde{\tilde{η}}}_{p 1}^{} * δ_{1}) - {\bar{\tilde{\tilde{ψ}}}}_{1} & \dots & ({\tilde{\tilde{η}}}_{p n}^{} * δ_{n}) - {\bar{\tilde{\tilde{ψ}}}}_{n} \end{matrix}) .

Step 7: Rank of all paths by using:

13

{\tilde{\tilde{θ}}}_{i} = \sum_{j = 1}^{n} {\tilde{\tilde{σ}}}_{i j} .

The results are ranked in descending orders.

3. Illustrative example

In this section, an illustrative example is presented and solved. Five efficient criteria (time, cost, risk, quality, and safety) are considered. The project network is represented in Fig. 1. Furthermore, the information about ratings of activity on efficient criteria is depicted in Table 3. The initial information of BWM method is depictured in Table 4.

The final results of the BWM method and final results of rankings are depicted in Table 5.

Fig. 1Project network

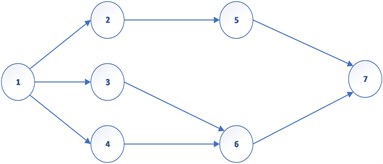
Table 3Activities’ ratings based on the efficient criteria

Act.	Expert’s judgment on time	Expert’s judgment on cost (100$)	Risk	Quality	Safety
1-2	((2, 4, 7, 8; 1, 1), (3, 5, 6, 7.5; 0.9, 0.9))	((5, 8, 11, 13; 1, 1), (6, 9, 10, 12; 0.9, 0.9))	VH	MH	M
1-3	((3, 5, 8, 10; 1, 1), (4, 6, 7, 9; 0.9, 0.9))	((2, 4, 6, 8; 1, 1), (3, 5, 5, 7; 0.9, 0.9))	H	MH	M
1-4	((5, 7, 9, 10; 1, 1), (6, 8, 8, 10; 0.9, 0.9))	((3, 5, 6, 8; 1, 1), (4, 5.5, 5.5, 7; 0.9, 0.9))	MH	H	ML
2-5	((3, 5, 7, 9; 1, 1), (4, 6, 6, 8; 0.9, 0.9))	((4, 6, 7.5, 8.5; 1, 1), (5, 7, 7, 8; 0.9, 0.9))	H	M	MH
3-6	((6, 8, 10, 12; 1, 1), (7, 9, 9, 11))	((4.5, 5.5, 6.5, 7.5; 1, 1), (5, 6, 6, 7; 0.9, 0.9))	H	ML	ML
4-6	((1, 3, 5, 7; 1, 1), (2, 4, 4, 6; 0.9, 0.9))	((1.5, 3.5, 4.8, 5.8; 1, 1), (2, 4, 4.5, 5.5; 0.9, 0.9))	MH	ML	H
5-7	((3, 4, 5, 7; 1, 1), (3, 4, 5, 6; 0.9, 0.9))	((2.83.6, 4.4, 5.2; 1, 1), (3, 4, 4.2, 5; 0.9, 0.9))	M	MH	VH
6-7	((5, 7, 9, 11; 1, 1), (6, 8, 9, 10; 0.9, 0.9))	((1, 2, 3.5, 4.5; 1, 1), (1.5, 2.5, 3, 4; 0.9, 0.9))	ML	M	H

Table 4Initial information for BWM method

Criteria	$Z_{1}$	$Z_{2}$	$Z_{3}$	$Z_{4}$	$Z_{5}$
Best criteria: $Z_{1}$	E	SS	FS	FS	VS
Worst criterion: $Z_{5}$	VS	FS	FS	SS	E

Table 5Final rankings of paths

Criteria	Weight	Paths	Value	Rankings
Time	0.49	1-2-5-7	0.046	2
Cost	0.21	1-3-6-7	–0.07	3
Risk	0.125	1-4-6-7	0.063	1
Quality	0.125
Safety	0.05

3.1. Comparative analysis

The BWABAC method is compared with the COPRAS method in order to demonstrate the validity and reliability of BWABAC method. The results are depictured in Table 7.

Table 7Comparative analysis

Paths	Final value of BWABAC	Rankings	Final value of COPRAS method	Rankings
1-2-5-7	0.046	2	1.299	2
1-3-6-7	–0.07	3	0.5977	3
1-4-6-7	0.063	1	1.47	1

4. Conclusions

In this paper, a new BWABAC method including the BWM and MABAC methods has been successfully applied to the critical path selection problem. All paths of projects have been modeled as alternatives and efficient criteria have been considered as criteria. To afford the uncertainty of practical situations, T2FSs have been applied. The membership degree of type-2 fuzzy sets is a classic fuzzy set, whereas, the membership degree of classic fuzzy sets is a crisp number. That is why T2FSs has been applied for critical path determination and inherent uncertainty of projects. Furthermore, the BWABAC method is extended under T2FSs.

Moreover, the BWABAC procedure has been checked with the well-known MCDM method (COPRAS). The results have been demonstrated the validity of the BWABAC method. The BWABAC method can be applied in all spectrum of areas of MCDM problems. For future work, BWABAC method can be developed under group decision-making problems. The subjective and objective procedures for determining the weight of members of group can be added to the BWABAC method.

References

Hofmann Peg A. Critical path method: an important tool for coordinating clinical care. The Joint Commission Journal on Quality Improvement, Vol. 19, Issue 7, 1993, p. 235-246.

Publisher
Zammori Francesco A., Braglia Marcello, Frosolini Marco A fuzzy multi-criteria approach for critical path definition. International Journal of Project Management, Vol. 27, Issue 3, 2009, p. 278-291.

Publisher
Amiri Maghsoud, Golozari Farhaneh Application of fuzzy multi-attribute decision making in determining the critical path by using time, cost, risk, and quality criteria. The International Journal of Advanced Manufacturing Technology, Vol. 54, Issues 1-4, 2011, p. 393-401.

Publisher
San Cristobal, Ramon Jose Critical path definition using multicriteria decision making: PROMETHEE method. Journal of Management in Engineering, Vol. 29, Issue 2, 2012, p. 158-163.

Publisher
Mehlawat Mukesh Kumar, Gupta Pankaj A new fuzzy group multi-criteria decision-making method with an application to the critical path selection. The International Journal of Advanced Manufacturing Technology, Vol. 83, Issues 5-8, 2016, p. 1281-1296.

Publisher
Mehlawat Mukesh Kumar, Grover Nishtha Intuitionistic fuzzy multi-criteria group decision making with an application to critical path selection. Annals of Operations Research, Vol. 269, Issues 1-2, 2018, p. 505-520.

Publisher
Pamučar Dragan, Ćirović Goran The selection of transport and handling resources in logistics centers using multi-attributive border approximation area comparison (MABAC). Expert Systems with Applications, Vol. 42, Issue 6, 2015, p. 3016-3028.

Publisher
Yu Su Min, Wang Jing, Wang Jian-Qiang An interval type-2 fuzzy likelihood-based MABAC approach and its application in selecting hotels on a tourism website. International Journal of Fuzzy Systems, Vol. 19, Issue 1, 2017, p. 47-61.

Publisher
Stević Željko, et al. Novel integrated multi-criteria model for supplier selection: Case study construction company. Symmetry, Vol. 9, Issue 11, 2017, p. 279.

Publisher
Ji Pu, Zhang Hong Yu, Wang Jian Qiang Selecting an outsourcing provider based on the combined MABAC-ELECTRE method using single-valued neutrosophic linguistic sets. Computers and Industrial Engineering, Vol. 120, 2018, p. 429-441.

Publisher
Rezaei Jafar Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega, Vol. 64, 2016, p. 126-130.

Publisher
Mohaghar Ali, Sahebi Iman Ghasemian, Arab Alireza Appraisal of humanitarian supply chain risks using best-worst method. International Journal of Social, Behavioral, Educational, Economic, Business and Industrial Engineering, Vol. 11, Issue 2, 2017, p. 309-314.

Search CrossRef
Amoozad Mahdiraji, Hannan, et al. A hybrid fuzzy BWM-COPRAS method for analyzing key factors of sustainable architecture. Sustainability, Vol. 10, Issue 5, 2018, p. 1626.

Publisher
Li Jian, Wang Jian-Qiang, Hu Jun-Hua Multi-criteria decision-making method based on dominance degree and BWM with probabilistic hesitant fuzzy information. International Journal of Machine Learning and Cybernetics, Vol. 10, Issue 7, 2019, p. 1671-1685.

Publisher
Zadeh Lotfi A. Fuzzy sets. Information and Control, Vol. 8, Issue 3, 1965, p. 338-353.

Publisher
Zadeh Lotfi A. The concept of a linguistic variable and its application to approximate reasoning – I. Information Sciences, Vol. 8, Issue 3, 1975, p. 199-249.

Publisher
Ghorabaee Mehdi Keshavarz Developing an MCDM method for robot selection with interval type-2 fuzzy sets. Robotics and Computer-Integrated Manufacturing, Vol. 37, 2016, p. 221-232.

Publisher
Balin Abit, Baracli Hayri A multi-criteria decision-making methodology suggestion for turkey energy planning based type-2 fuzzy sets. Decision Making, Vol. 5, 2018, https://doi.org/10.5772/intechopen.75303.

Publisher
Lee L. W., Chen S. M. A new method for fuzzy multiple attributes group decision-making based on the arithmetic operations of interval type-2 fuzzy sets. International Conference on Machine Learning and Cybernetics, Vol. 6, 2008, p. 3084-3089.

Search CrossRef
Dorfeshan Y., Mousavi S. M., Mohagheghi V., Vahdani B. Selecting project-critical path by a new interval type-2 fuzzy decision methodology based on MULTIMOORA, MOOSRA and TPOP methods. Computers and Industrial Engineering, Vol. 120, 2018, p. 160-178.

Publisher

About this article

Received

26 October 2019

Accepted

19 November 2019

Published

07 May 2020

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2019.21125

Keywords

critical path method (CPM)

type-2 fuzzy sets (T2FSs)

MABAC approach

BWM approach

BWABAC approach

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 05 18

Uncertain optimization for composite base plate of mortar under impact load

Fengfeng Wang, Guolai Yang, Fengjie Xu

Research article

2022 07 27

Active damping control of HEVs using Ansys and Matlab/Simulink software

Tewodros Kassa Mersha, Changqing Du

Research article

2019 12 31

Selection of ground motion prediction equations for probabilistic seismic hazard analysis based on an improved fuzzy logic

Mohsen Ali Shayanfar, Mohammad Ali Barkhordari, Mostafa Mahmoudi, Ehsan Jahani

Research article

2019 10 19

Investigation and optimization of the cable force of a combined highway and railway steel truss cable-stayed bridge in completion state

Haohong Li, Shuyang Liu, Qiuwei Shan, Liangliang Zhang, Bo Wu

K. Noshadpoor, “Evaluation of critical path of construction projects by using the new BWABAC method under uncertainty,” Vibroengineering PROCEDIA, Vol. 31, pp. 122–128, May 2020, https://doi.org/10.21595/vp.2019.21125

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.21125
UR  - https://doi.org/10.21595/vp.2019.21125
TI  - Evaluation of critical path of construction projects by using the new BWABAC method under uncertainty
T2  - Vibroengineering PROCEDIA
AU  - Noshadpoor, Keivan
PY  - 2020
DA  - 2020/05/07
PB  - JVE International Ltd.
SP  - 122-128
VL  - 31
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Noshadpoor_2020,
	doi = {10.21595/vp.2019.21125},
	url = {https://doi.org/10.21595/vp.2019.21125},
	year = 2020,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {31},
	pages = {122--128},
	author = {Keivan Noshadpoor},
	title = {Evaluation of critical path of construction projects by using the new {BWABAC} method under uncertainty},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]K. Noshadpoor, “Evaluation of critical path of construction projects by using the new BWABAC method under uncertainty,” Vibroengineering PROCEDIA, vol. 31, pp. 122–128, May 2020, doi: 10.21595/vp.2019.21125.

Copy IEEE

Copied to clipboard!

Noshadpoor, Keivan. “Evaluation of Critical Path of Construction Projects by Using the New BWABAC Method under Uncertainty.” Vibroengineering PROCEDIA 31 (May 7, 2020): 122–28. https://doi.org/10.21595/vp.2019.21125.

Copy Chicago

Copied to clipboard!

Evaluation of critical path of construction projects by using the new BWABAC method under uncertainty

Abstract

Highlights

1. Introduction

2. Suggested method

3. Illustrative example

3.1. Comparative analysis

4. Conclusions

References

About this article

Related Articles