Abstract
Information warfare places higher requirements on the remoteness, precision and mobility of artillery weapon systems. As an indispensable and important category of artillery, mortar plays an important role. As an important component of mortar, the base plate bears tremendous impact load. Its design level has an important influence on the shooting stability, shooting accuracy and maneuverability of the mortar. Composite base plate helps improve the maneuverability of the mortar, but it will also make the force and movement rule of mortar launching more complex and lead to a more acute contradiction between artillery power and maneuverability, which propose a huge challenge to modern artillery optimization design theory. Under this background, this manuscript conducts research on the structural uncertain optimization of composite material base plate for the mortar. In order to obtain the optimal solution and reasonable interval of uncertain parameters with main dimension parameters, this manuscript uses interval model to carry out deterministic transformation for uncertain objective function and uncertain constraints, combines multi-objective genetic algorithm to solve the problem, and carries out numerical simulation to verify the optimal value. The result shows that the design idea and method are feasible for uncertain optimization of composite base sheet of mortar under impact load, and the optimization objectives and strategies are effective, which can provide reference for the uncertain optimization research of composite base plate.
1. Introduction
In the information age, with the focus shifting towards digital battlefields and remote precision strikes, targets display strong maneuverability and rapid changes, while fighter planes make swift maneuvers. This imposes much higher demands on the remote precision mobility of artillery weapon systems. As an indispensable and important category of artillery, mortar plays an important role. Because the quality of the base plate accounts for a large proportion in mortars, the key to improving the mobility of mortars is to improve the mobility of the base plate. The use of composite material base plate can improve mobility, but this will make the force and motion laws of the artillery firing process more complex, leading to a sharper contradiction between the power and mobility of mortars. On the one hand, the existing design theories generally treat artillery as a deterministic system and use deterministic theory to establish a dynamic model of the artillery firing process. However, the artillery firing process is essentially an uncertain process affected by uncertain factors, and it is difficult to obtain effective design results directly using existing deterministic design theories. On the other hand, the performance indicators such as shooting accuracy and maneuverability of mortars are often contradictory, conflicting, and mutually constraining, and existing artillery optimization methods are difficult to effectively address this contradiction. Previous research on composite base plate generally used finite element methods combined with lightweight composite layer optimization [1], [2]. However, due to the initial stage of research, the uncertainty of structural parameters was ignored [3], [4]. The progress of theory and technology has fully recognized the importance of conflict of objectives and uncertainty, and uncertainty optimization technology has gradually been applied to reliability optimization, topology optimization, vehicle optimization, power system optimization and other fields [5]. They generally use interval models and probability models, to optimize uncertainty parameters and obtain the optimal solution and reasonable interval [6], [7]. Among them, the interval model uses interval numbers as a mathematical tool to describe parameter uncertainty, without the need for precise probability distribution of parameters, only knowing the upper and lower bounds of the parameters. The interval optimization method derived from interval mathematics, as a non-probabilistic uncertainty optimization method, provides an economical and efficient solution for engineering optimization problems that probability methods are difficult to solve. Jiang et al. [8], [9] transformed the uncertain objective function into two deterministic objective functions based on the interval order relationship, and improved an interval likelihood model to convert the uncertain constraint function into a deterministic constraint, further extending this method to general uncertain structural optimization. Under this background, the manuscript conducts exploratory research on the structural uncertainty optimization problem of composite base plate of the mortar.
2. Model basics
2.1. Load
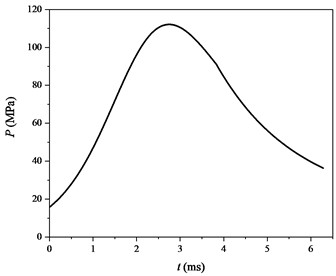
The firing process in the mortar chamber is a complex and transient physical and chemical process. Based on multiphase fluid mechanics theory and combustion theory, the purpose of these equations is to implement numerical simulation of the firing process. As shown in Fig. 1, before igniting the gunpowder, the propellant is loaded into the mortar tube from the rear chamber to the bottom of the projectile; after the combustion of gunpowder, propellant, also known as propellant, regularly burns to release energy, produce gas, and push the gunpowder of the missile; when dispersed in the gas phase, they have fluid properties [9]. The pressure curve generated at the bottom of the mortar barrel during gunpowder combustion is shown in Fig. 2. When a mortar is fired with full charge, the impact load on the base plate is about 112 MPa and the duration is about 6 ms.
Fig. 1Schematic drawing of propellant location

Fig. 2Pressure curve
2.2. Model
This manuscript focuses on the trapezoidal pyramid base plate for a large caliber mortar, as shown in Fig. 3. Due to its comprehensive advantages of other base plate structures, it has the characteristics of preventing jumping and ensuring stable and safe shooting, and is widely used in active mortar in various countries. According to the structural characteristics of the metal base plate shown in Fig. 3, the composite base plate skeleton structure was designed and obtained by using the topology optimization method based on sensitivity analysis, as shown in Fig. 4 [10]. The skeleton material is still made of titanium alloy, and the hollow part in Fig. 4 is made of carbon fiber composite.
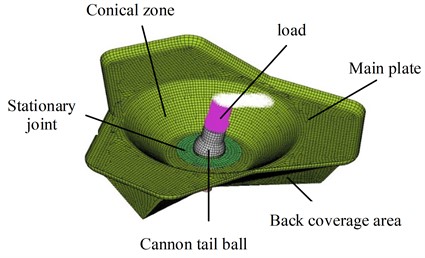
After meshing, defining attributes, setting contact relationships, and determining boundaries, the bottom pressure curve in Fig. 2 is uniformly applied to the upper section of the gun tail ball, and constraint conditions are set to obtain the finite element model of the composite material base plate to be optimized, as shown in Fig. 5. The design of the composite layer follows the principles of directional and balanced/symmetrical laying, select the laying direction according to the load type, reasonably select the laying sequence according to the minimum proportion, and to ensure that there are enough fibers laid in the impact load direction of the laminated board to withstand local impact loads, we select the [+45°/–45°/0°/90°]s laying method.
Fig. 3The titanium alloy base plate

Fig. 4Titanium alloy skeleton of the composite base plate
Fig. 5Finite element model of composite base plate
3. Uncertainty optimization of composite base plate
3.1. Uncertainty optimization of composite base plate
In this study, the upper and lower intervals of a uniform distribution are represented by uncertain parameters, and the membership function of the parameters do not need to be known. Therefore, interval methods are chosen to optimize the uncertainty. Specifically, it can be expressed as:
where is an uncertainty interval vector consisting of an n-dimensional interval vector . The superscripts , , , and represent the lower, upper, center, and radius of the interval, respectively. and denote the uncertain objective function and constraints for interval optimization, respectively. The uncertain design variables considered in this manuscript include 5, namely titanium alloy skeleton, Stationary joint, Cone-shaped basin, Main plate, Backside composite cladding area. Their specific locations are shown in Fig. 4 and Fig. 5. Based on past design experience, Table 1 lists the initial values and ranges of design variables. The original mass of the base plate is 52.76 kg.
Table 1Design variables
Parameter | Titanium alloy skeleton | Stationary joint | Conical zone | Main plate | Back coverage area |
Initial (mm) | 6 | 10 | 15 | 6 | 6 |
Lower (mm) | 1 | 5 | 5 | 1 | 1 |
Upper (mm) | 10 | 20 | 20 | 10 | 10 |
3.2. Treatment of the uncertain objective function and constraints
To handle the uncertain objective functions in this study, the interval order relation proposed by Jiang [9] was adopted. The relation states that interval B is better than interval A only when both the radius and midpoint of interval B are smaller than those of interval A. The objective function and constraints for determining multi-objective need to be transformed into multi-objective optimization problems through Eq. (2):
Here, and represent the upper and lower bounds of the objective function, separately:
It refers to the probability of a random variable from interval A being smaller or larger than interval B. The NSGA-II algorithm is employed to obtain the optimal solution, with GA serving as the inner optimizer. The reliability test in this study employs the determination coefficient, is a value that ranges from 0 to 1. with higher values indicating greater fitting accuracy. To obtain test samples within the design space, the OLHD method is used. The result of value is approximately 0.96, indicating that the approximate model is acceptable.
3.3. Results
It illustrates a set of non-dominated solutions in Fig. 6, which are located in the front of Pareto optimality. Point A is chosen from this group of solutions as the final design scheme, and the corresponding intervals for each design variable can be found in Table 2.
The results are as shown in Table 3. The mass of composite base plate is 49.85 kg, which is 5.52 % less than the initial mass.
Set the calculation condition of 0° direction angle and 75° high and low angle, calculate the strength and displacement of composite base plate before and after optimization. The comparison nephograms are shown in Fig. 7 and Fig. 8.
Fig. 6Pareto front
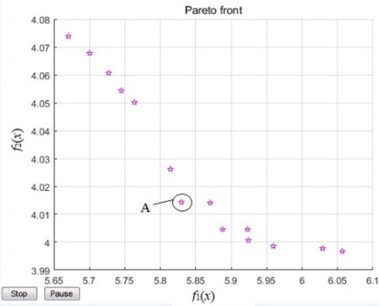
Table 2Intervals of the design variables
Parameter | Before (mm) | After (mm) | Changes of before and after optimization | ||
Variation range | Change range | Variation range | Change range | ||
Titanium alloy skeleton | 1-10 | 9 | 4-8.5 | 4.5 | –4.5 |
Stationary joint | 5-20 | 15 | 10-16.5 | 6.5 | –8.5 |
Conical zone | 5-20 | 15 | 8-12 | 4 | –9 |
Main plate | 1-10 | 9 | 5-8 | 3 | –6 |
Back coverage area | 1-10 | 9 | 6-8 | 2 | –7 |
Table 3Values and ranges of design variables
Parameter | Titanium alloy skeleton | Stationary joint | Conical zone | Main plate | Back coverage area |
Initial (mm) | 4 | 11 | 8 | 5 | 6 |
From the stress and strain nephogram of the base plate, it can be seen that the maximum stress of the optimized base plate is reduced compared to before optimization, which can satisfy intensity requirement. But the maximum strain of the optimized base plate has slightly increased compared to before optimization, which falls within the design scope and satisfies the design requirement.
Fig. 7Stress nephogram
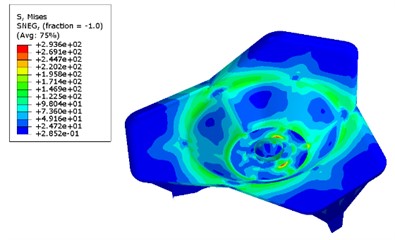
a) Before optimization
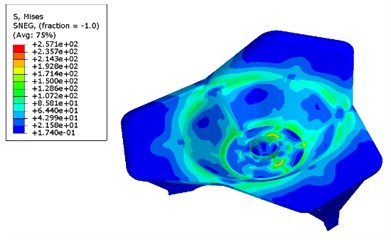
b) After optimization
Fig. 8Strain nephogram
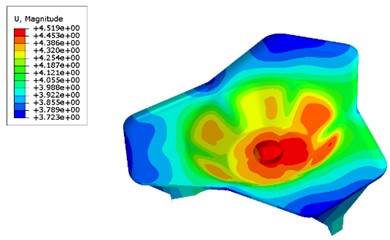
a) Before optimization
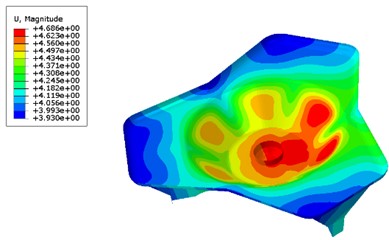
b) After optimization
4. Conclusions
The uncertain parameters and increasingly sharp contradiction between the technical and tactical indicators of artillery weapon systems propose a huge challenge to modern artillery optimization design theory. This manuscript focuses on the uncertainty optimization research of the main structure of composite material base plate for the mortar, which is an attempt and exploration of uncertainty optimization technology in the study of mortar dynamics. The results indicate that the research method is feasible, and the optimization results can meet the design requirements, providing a new approach for the design optimization of composite material base plate, which is of great significance for improving the maneuverability of mortars.
References
-
X. Wang, Optimal Design of a Large Caliber Mortar Base Plate Structure. Nanjing: Nanjing University of Technology, 2019.
-
X. Wang et al., “Lightweight design of mortar base plate,” (in Chinese), Journal of Artillery Launch and Control, Vol. 39, No. 4, pp. 54–59, 2018, https://doi.org/10.19323/j.issn.1673-6524.2018.04.011
-
F. Wang et al., “Research on the test and lightweight design of a mortar base plate,” (in Chinese), Vibration and Shock, Vol. 39, No. 17, pp. 76–81, 2020, https://doi.org/10.13465/j.cnki.jvs.2020.17.011
-
J. Ge, X. Xie, Q. Sun, and G. Yang, “Design and dynamic characteristics of a double-layer permanent-magnet buffer under intensive impact load,” Journal of Sound and Vibration, Vol. 506, No. 6, p. 116158, Aug. 2021, https://doi.org/10.1016/j.jsv.2021.116158
-
C. Wang and H. G. Matthies, “Epistemic uncertainty-based reliability analysis for engineering system with hybrid evidence and fuzzy variables,” Computer Methods in Applied Mechanics and Engineering, Vol. 355, pp. 438–455, Oct. 2019, https://doi.org/10.1016/j.cma.2019.06.036
-
L. Wang, G. Yang, Q. Sun, and J. Ge, “An uncertain optimization method for overall ballistics based on stochastic programming and a neural network surrogate model,” Engineering Optimization, Vol. 51, No. 4, pp. 663–679, Apr. 2019, https://doi.org/10.1080/0305215x.2018.1484122
-
F. Xu, G. Yang, L. Wang, and Q. Sun, “Interval uncertain optimization for interior ballistics based on Chebyshev surrogate model and affine arithmetic,” Engineering Optimization, Vol. 53, No. 8, pp. 1331–1348, Aug. 2021, https://doi.org/10.1080/0305215x.2020.1790551
-
C. Jiang, X. Han, and G. P. Liu, “A sequential nonlinear interval number programming method for uncertain structures,” Computer Methods in Applied Mechanics and Engineering, Vol. 197, No. 49-50, pp. 4250–4265, Sep. 2008, https://doi.org/10.1016/j.cma.2008.04.027
-
C. Jiang et al., “Interval uncertain optimization of vehicle suspension for ride comfort,” Computer Modeling in Engineering and Sciences, Vol. 98, No. 4, pp. 443–467, 2014.
-
F. Wang, G. Yang, J. Ge, and F. Xu, “Lightweight design of a certain mortar base plate based on sensitivity analysis,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 43, No. 3, pp. 1–13, Mar. 2021, https://doi.org/10.1007/s40430-021-02864-2
About this article
This work supported by research project for high-level talents of Jinling Institute of Technology (No. jit-b-202227), China.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
