Abstract
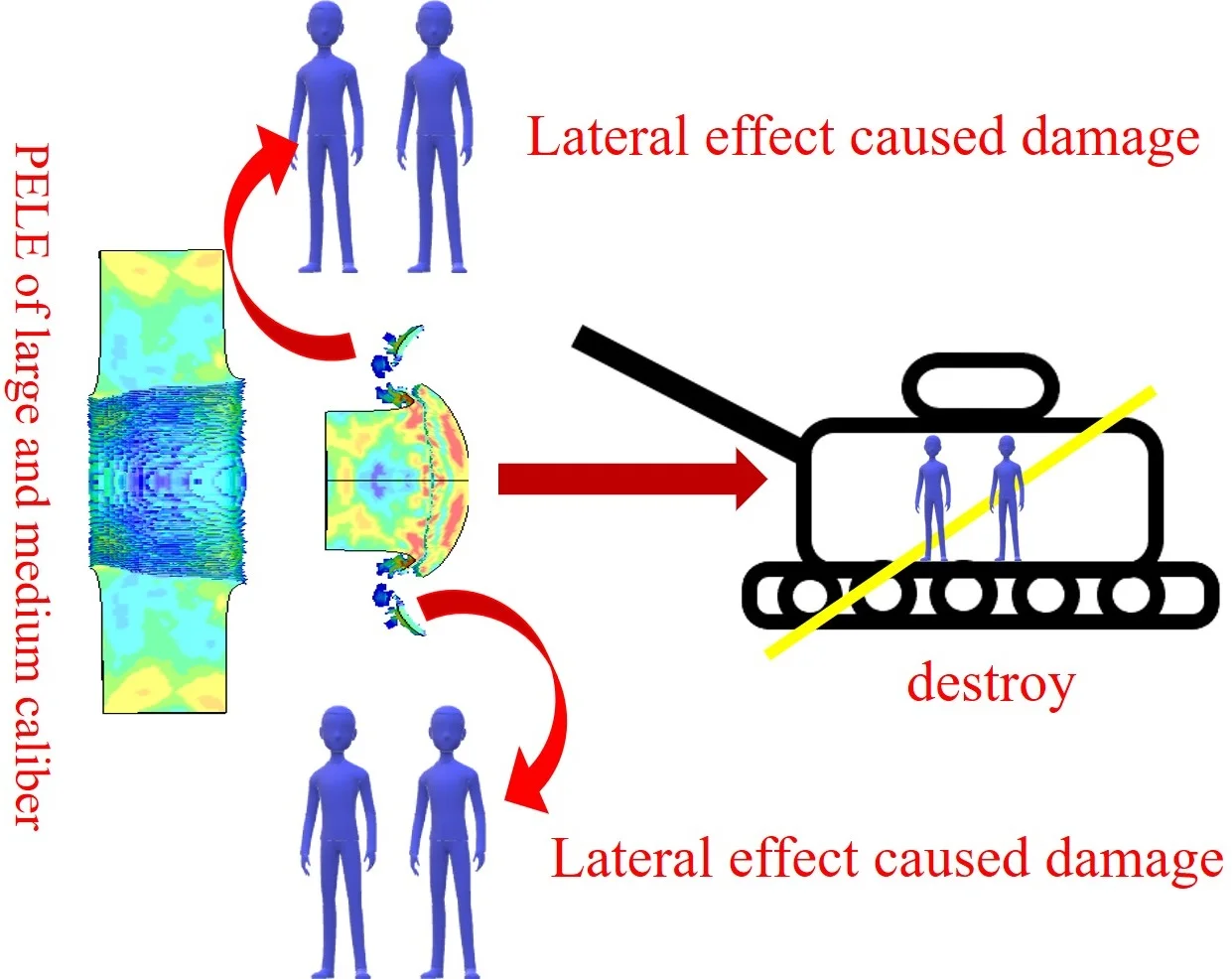
PELE (Penetrator with Enhanced Later Effect) is a new type of ammunition, which does not need to be filled with explosives and fuses, but has the function of armor piercing projectile and grenade at the same time. The numerical simulation of a 60 mm diameter PELE penetrating target was investigated. The results show that in the process of the target plate becoming thicker, the transverse effect first increases and then weakens, and the optimal target plate thickness range is 4-6 cm; the properties of the core material have an important influence on the transverse effect of PELE; with the increase of the core radius, the radial velocity of the fragments after PELE penetrating the target first increases, then decreases and then increases, and the optimal core radius is 2-2.6 cm.
1. Introduction
With the increase of the diversity of targets and the mobility of protection, the traditional penetration warhead cannot meet the needs of modern battlefield gradually, and the penetrator with enhanced later effect (PELE) is born. PELE is mainly used in the fields of air defense, anti missile, anti ground and sea light armor. After the projectile penetrates the target plate, the constraint around the inner core material disappears suddenly, and the shell body breaks into a large number of fragments distributed along the radial direction under the effect of radial pressure.
Paulus [1] established the theoretical calculation model of the axial residual velocity of the projectile after PELE penetrating the target, based on the one-dimensional linear wave theory and the momentum conservation law. Shengyuan Tu [2] through the numerical simulation of the terminal effect and the comparative experiment with the penetration of the same caliber ordinary armor piercing projectile into the steel plate, it is proved that there are three key stages in the mechanism of PELE projectile's impact on the steel plate: impact coarseness, expansion penetration and penetration burst. Pengyuan Ji [3] gave the calculation method of the residual velocity of the projectile under the forward and oblique penetration of PELE, and calculated the limit ballistic velocity of the PELE projectile. Analysis shows that the core material has little effect on the penetration ability of PELE projectiles. Verreault [4] analyzed the interaction between the PELE shell and the inner core, and obtained the velocity model of the fragments flying along the radial direction after the PELE penetrating the target. Zijian Fan [5] studied the radial flying velocity of the projectile fragments after the PELE projectile penetrated the thin plate. By analyzing the axial and radial deformation of the projectile during the penetration process, he proposed the "two process" analysis method of the projectile deformation, and gave the calculation model of the radial flying velocity of the fragments after the projectile target.
Many scholars have done researches on PELE, most of them focus on small caliber PELE, but few on large and medium caliber PELE. Based on the research results of scholars at home and abroad, this paper conducts numerical simulation of the whole process of the interaction performance of the lateral effect enhanced penetrator on the target plate structure, studying and analyzing the influence of the target plate thickness, the core material and the core radius on the lateral effect of PELE. It can provide some reference value for the optimization design and improvement of PELE.
2. Calculation model
The numerical simulations of projectile penetrating target plate with enhanced lateral effect are performed with the commercial finite element code LS-DYNA, as shown in Fig. 1. The calculation model includes shell, core and target plate. Lagrange grid is adopted for both target plate and projectile body. By using the inherent symmetry of the studied problem, calculation time can be saved. Thus, only a quarter of the cylindrical shell was modeled with the appropriate boundary conditions applied along the symmetry planes. Symmetrical constraints are set on the symmetrical surface, and fixed constraints are set on the outside of the asymmetric boundary. The projectile penetrates the metal target plate vertically at a speed of 1400 m/s, and the parameters of the projectile and the target plate are shown in Table 1.
Fig. 1The numerical model
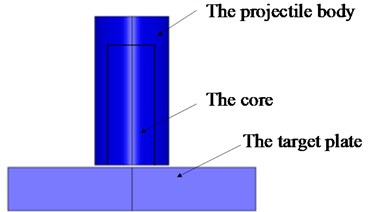
Table 1The parameters of the projectile and the target plate
Working condition | Shell material | Core material | Body height | Body radius | Core radius and height | Target plate thickness |
A | Steel | Aluminum alloy | 137 mm | 30 mm | 24 mm×100 mm | 2 cm |
B | Steel | Aluminum alloy | 137 mm | 30 mm | 24 mm×100 mm | 4 cm |
C | Steel | Aluminum alloy | 137 mm | 30 mm | 24 mm×100 mm | 6 cm |
D | Steel | Aluminum alloy | 137 mm | 30 mm | 24 mm×100 mm | 8 cm |
E | Steel | Aluminum alloy | 137 mm | 30 mm | 16 mm×100 mm | 4 cm |
F | Steel | Aluminum alloy | 137 mm | 30 mm | 18 mm×100 mm | 4 cm |
G | Steel | Aluminum alloy | 137 mm | 30 mm | 20 mm×100 mm | 4 cm |
H | Steel | Aluminum alloy | 137 mm | 30 mm | 22 mm×100 mm | 4cm |
I | Steel | Aluminum alloy | 137 mm | 30 mm | 24 mm×100 mm | 4cm |
J | Steel | Aluminum alloy | 137 mm | 30 mm | 26 mm×100 mm | 4 cm |
K | Steel | Aluminum alloy | 137 mm | 30 mm | 28 mm×100 mm | 4 cm |
L | Steel | Plastic | 137 mm | 30 mm | 24 mm×100 mm | 4 cm |
M | Steel | Aluminum alloy | 137 mm | 30 mm | 24 mm×100 mm | 4 cm |
3. Results and analysis
3.1. The influence of target plate thickness
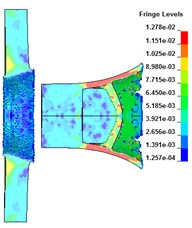
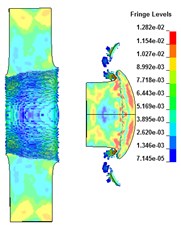
Numerical analysis is carried out for the projectile penetrating the target plate under the conditions of A, B, C and D. The deformation of the target plate and the projectile body is shown in Fig. 2.
Fig. 2The deformation of the target plate and the projectile body
a) A
b) B
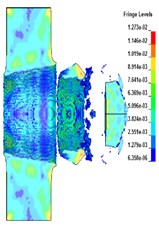
c) C
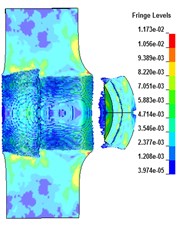
d) D
It can be seen from Fig. 2 that after the penetration of PELE into the target plate, the remaining length of its rod gradually becomes shorter, but there are residual velocities. The thickness of the target plate is different, and the way of PELE forming the lateral effect is different. When the target thickness is 4 cm, the shell is broken to form fragments, and when the target thickness is 6 cm, the shell is broken inside the target plate, making the target plate form a large number of fragments after the target.
Under different target thicknesses, the variation of residual velocity of projectile body with the thickness of target plate is shown in Table 2. It can be seen that with the increase of the thickness of the target plate, the more materials the projectile consumes in the penetration stage of the projectile into the target plate, so the length of the projectile rod becomes shorter gradually. Due to the thickness of the target plate, the stronger the blocking effect of the target plate on the projectile rod, resulting in the gradual decrease of the speed of the remaining projectile rod and the gradual decrease of the lethality after the target. When the target thickness is between 4 cm and 8 cm, the radius of the transverse effect area increases first and then decreases, and the radial velocity of fragments also increases first and then decreases.
Table 2The variation of residual velocity of projectile body with the thickness of target plate
The thickness of target plate (cm) | 2 | 4 | 6 | 8 |
Residual velocity of projectile body (m/s) | 1236.9 | 999.1 | 805.4 | 212.8 |
3.2. The influence of core radius
The deformation and failure of the target plate under different core radius are shown in Fig. 3. It can be seen that when 158 μs, the projectile penetrates the target plate and is behind the target plate. With the increase of the core radius, the lateral effect of PELE projectile first increases and then weakens. When 24 mm, the lateral effect is the most obvious. Under the condition of different core radius, the target plate forms damage fragments behind the target, achieving the effect of transverse effect. When the radius of the core is 28 mm, a small number of fragments are formed after the target plate is broken. When the radius is less than 24 mm, the projectile shell can be broken to form fragments.
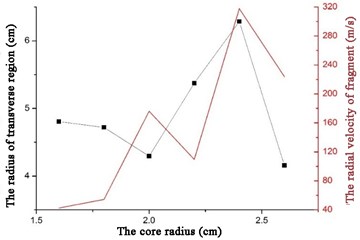
Fig. 4 shows the relationship between the radius of the transverse region and the radial velocity of fragments formed by PELE with 150 μs. It can be seen from the figure that the transverse area formed by the fragments formed after the target increases first and then decreases with the increase of the core radius; when the core radius is fixed, the transverse area radius of the PELE increases with the increase of time. The radial velocity of the fragments formed by PELE increases first and then decreases with the increase of the radius of the core; when the radius of the core is fixed, the radial velocity of the fragments increases first and then decreases and then increases and then decreases with the increase of the time, among which the maximum value is achieved at the moment after penetrating the target plate. After comprehensive comparison, it can be concluded that PELE, which can achieve good lateral effect after target, has a core radius of 2 cm-2.6 cm.
Fig. 3The deformation of the target plate and the projectile body (t= 158 μs)
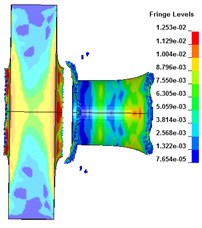
a) E (16 mm)
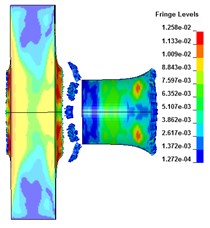
b) F (18 mm)
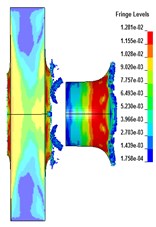
c) G (20 mm)
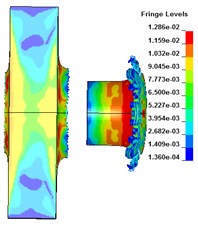
d) H (22 mm)
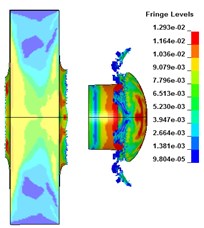
e) I (24 mm)
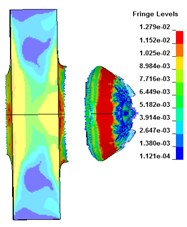
f) J (26 mm)
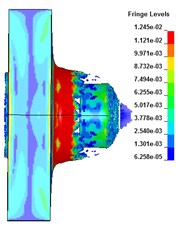
g) K ( 28 mm)
Fig. 4Relationship between radius of transverse region and radial velocity of fragment with radius
3.3. The effect of core material
In order to better compare the influence of different core materials on the lateral effect of PELE, plastic and aluminum alloy are selected as core materials in this paper. Corresponding to the working conditions L and M, the numerical simulation is carried out respectively, and the results are shown in Fig. 5.
The flying radius of fragments under different core materials is shown in Fig. 6. It can be seen from the figure that when 156 μs, the radius of fragments generated by the PELE with the core material of aluminum alloy is 6.4 cm, while the PELE with the core material of plastic has no fragments. Therefore, under certain conditions, the aluminum alloy material is most suitable for the vertical penetration of 60 mm PELE into the metal target plate to produce the transverse effect.
Fig. 5The deformation of the target plate and the projectile body under different core materials
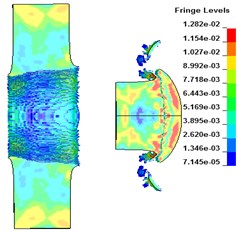
a) Aluminum alloy
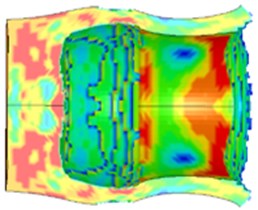
b) Plastic
Fig. 6The fragment flying radius under different core materials (t= 156 μs)
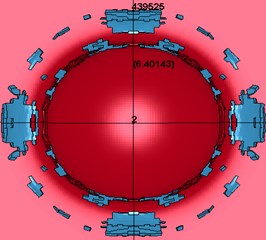
a) Aluminum alloy: 6.4 cm
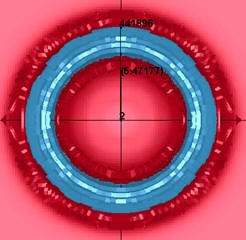
b) Plastic: none
4. Conclusions
1) Numerical simulations were performed for PELE to penetrate vertically into homogeneous steel plates of different thicknesses at a fixed target speed. The results show that the transverse effects of PELE penetrating different thicknesses targets vary with the thickness of the target. In the process of target plate thickening, the length of residual rod becomes shorter after PELE penetrates the target plate, the axial residual velocity of projectile penetrates the target plate decreases slowly, and the radial velocity of fragment increases first and then decreases; when the target plate thickness increases to a certain degree, most of the energy dissipation of PELE is in the process of armor piercing, and the transverse effect is significantly weakened.
2) Within a certain radius of the core, the projectile shell can be broken into metal fragments. PELE can achieve good lateral effect after target, which can be formed by fragmentation of projectile shell or target plate. The radius range of the projectile core which can achieve the good effect of the lateral effect behind the target is 2 cm-2.6 cm.
3) For plastic loading material, there is no fragment after penetrating the target plate, and the killing effect is poor. Therefore, for plastic and aluminum alloy, aluminum alloy material is better for projectile core.
References
-
Paulus C., Schirm V. Impact behavior of PELE projectiles perforating thin target plates. International Journal of Impact Engineering, Vol. 33, Issue 1, 2006, p. 566-579.
-
Gurney R. W. The Initial Velocities of Fragments from Bombs, Shell and Grenades. Ballistic Research Laboratory, Aberdeen, Report No. 405, 1943.
-
Tu Shengyuan, Wang Junbo, An Zhentao, Chang Yue Influence of thickness of armor on the burst-effect of steel shell PELE. The Ninth International Conference on Electronic Measurement and Instruments, Vol. 4, 2009, p. 926-929.
-
Ji Pengyuan, Wang Haifu Ballistic limit and residual velocity of PELE penetrating against metal target. Journal of Beijing Institute of Technology, Vol. 20, 2011, p. 183-186.
-
Fan Zijian, Ran Xianwen, Tang Wenhui, et al. The model to calculate the radial velocities of fragments after PELE perforating a thin plate. International Journal of Impact Engineering, Vol. 95, 2016, p. 12-16.
About this article
This research was financially supported by the National Nature Science Foundation of China, Nos. 51978660 and 51678567, and the China Postdoctoral Science Foundation Nos. 2018M633753.
