Sliding-mode control for coal shearer drum height adjustment based on variable speed reaching law

2.1. Machine-electric-liquid multiple field coupling coal shearer height adjustment system

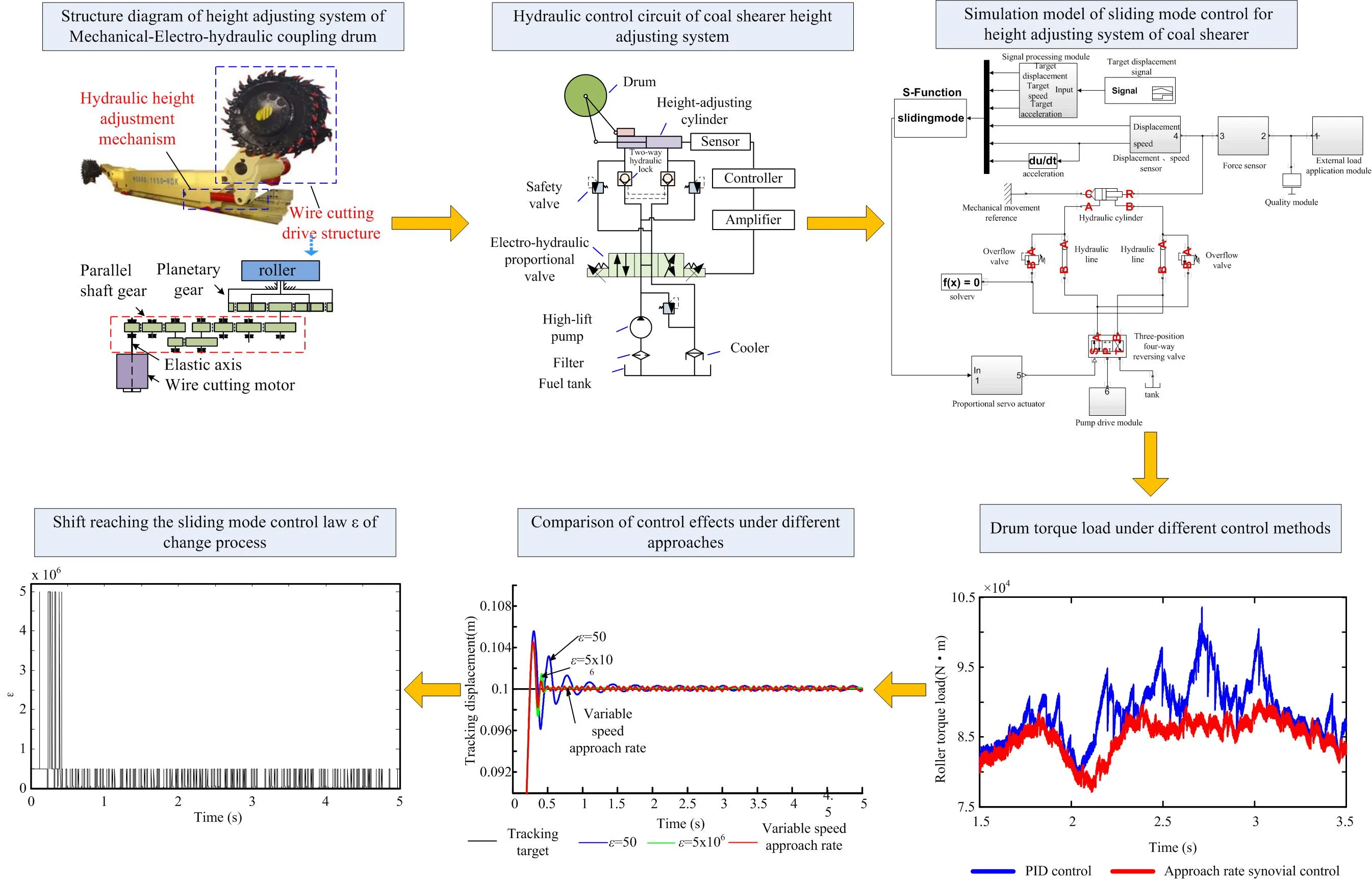
The coal shearer drums height adjustment system mainly includes a drum cutting transmission mechanism and a height adjustment mechanism. The drum cutting mechanism is composed of a cutting motor, a gear transmission system, a drum, etc.; the hydraulic height adjusting mechanism is composed of a driving motor, a control system, a hydraulic motor and a hydraulic cylinder. The structure diagram of the “machine-electric-liquid” coupling drum height adjustment system is shown in Fig. 1.

2.2. Increase control system transfer function

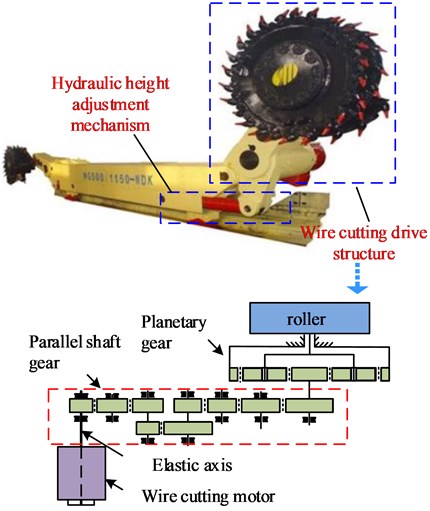
The hydraulic control circuit diagram of the coal shearer machines height adjustment system is shown in Fig. 2. It includes the electro-hydraulic proportional valve, height-adjusting pump, height-adjusting cylinder and two-way hydraulic lock. When the coal smasher height adjustment system is working, the controller gives the control voltage (the input quantity of the system), and after the amplifier is amplified, the current control signal is obtained, and the throttle area is controlled to change accordingly. Thereby changing the flow rate of the system to control the trajectory and lifting speed of the adjusting drum. The displacement sensor is used to detect the displacement of the cylinder piston, and the signal is converted and compared with a given target signal to form a closed loop control system.

Fig. 1Structure diagram of height adjusting system of Mechanical-Electro-hydraulic coupling drum

According to the force balance equation of the drum height-adjusting cylinder and the flow continuity equation of the cylinder [17], the external load disturbance during the piston movement is ignored, and the closed-loop transfer function of the servo valve of the coal-fired electro-hydraulic proportional-increasing system is as follows:

Among them: ${\omega }_h=\sqrt{4{\beta }_e{A_p}^2/V_{t}m}$, ${\xi }_h=(K_{ce}\sqrt{{\beta }_{e}m/V_t}+B_p\sqrt{V_t/16{\beta }_{e}m})/A_p$. Where $X_p$ is the displacement of the piston of the cylinder; $U$ is the control voltage signal; $A_p$ is the effective area of the piston inside the cylinder; $K_q$, $K_a$ and $K_{sv}$ are the flow gain, amplifier gain and proportional valve gain; ${\xi }_h$ and ${\omega }_h$ are the damping ratio and natural frequency of the system; $V_t$ is the total compression volume of the hydraulic cylinder; ${\beta }_e$ is the effective volume elastic modulus; $m$ is the total mass of the piston and the load converted to the piston; $B_p$ is the damping coefficient of the moving parts such as the piston and the load.

2.3. State space model

According to the transfer function, the system state space equation is:

In the middle:

Fig. 2Hydraulic control circuit of coal shearer height adjusting system

Define $r$ as the signal for the given position. If the deviation $e$ of the system is a state variable, then:

According to Eqs. (3) and (1), the state space model of the electro-hydraulic proportional servo system based on the deviation variable is obtained as follows:

In the formula:

3.1. Sliding mode switching surface design

Select the sliding surface switching function:

The exponential approach law expression is:

If the generalized sliding mode condition is satisfied at the same time, when $s>0$, $\dot{s}=-\epsilon -ks$; $s\left(t\right)=-\frac{\epsilon }{k}+\left(s_0+\frac{\epsilon }{k}\right)e^{(-kt)}$; When $s<0$, $\dot{s}=\epsilon -ks$, $s\left(t\right)=\frac{\epsilon }{k}+\left(s_0+\frac{\epsilon }{k}\right)e^{(-kt)}$. In the formula, $s_0$ is the initial value of the switching function $s$, $k$ is the approaching speed index, $\epsilon$ is the arrival speed, and $t$ is the time.

3.2. Design of sliding mode control function

To get the near-law control, there are:

where $r_{law}$ is the chosen approach law.

For the electro-hydraulic proportional servo system to select the function switching control strategy, then:

According to Eqs. (4) and Eqs. (5):

When the generalized sliding mode condition is satisfied $s\dot{s}<0$, according to Eq. (8) and Eq. (9):

According to Eq. (6) and Eq. (9):

According to Eq. (11), the sliding mode control function is:

Construct the Lyapunov function $V=s^2\mathrm{}\mathrm{A}\mathrm{D}\mathrm{D}\mathrm{I}\mathrm{N}\mathrm{}\mathrm{}\mathrm{E}\mathrm{N}.\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{E}\mathrm{}<\mathrm{E}\mathrm{n}\mathrm{d}\mathrm{N}\mathrm{o}\mathrm{t}\mathrm{e}><\mathrm{C}\mathrm{i}\mathrm{t}\mathrm{e}><\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{N}\mathrm{u}\mathrm{m}>0</\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{N}\mathrm{u}\mathrm{m}><\mathrm{N}\mathrm{o}\mathrm{t}\mathrm{e}>²</\mathrm{N}\mathrm{o}\mathrm{t}\mathrm{e}><\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{T}\mathrm{e}\mathrm{x}\mathrm{t}>²</\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{T}\mathrm{e}\mathrm{x}\mathrm{t}></\mathrm{C}\mathrm{i}\mathrm{t}\mathrm{e}></\mathrm{E}\mathrm{n}\mathrm{d}\mathrm{N}\mathrm{o}\mathrm{t}\mathrm{e}>/2$, then:

It can be seen from the above formula that $\dot{V}<0$ the system designed is stable in accordance with the existence and accessibility conditions of the sliding mode.

4.1. Establishment of hydraulics analog simulation model

In the simulation study of the dynamic performance of the electro-hydraulic servo system, the simulation model is established based on the derived system transfer function of Simulink software, and the system is improved according to the simulation results until the dynamic characteristics meet the requirements. However, such models do not consider nonlinear factors such as pipe connection, coulomb friction, and hydraulic oil source and so on, which are too idealistic. And there are errors compared with the actual situation which cause the simulation results are not accurate enough. In addition, the traditional simulation method also has the disadvantages of cumbersome and not intuitive modeling process.

Hydraulics Analog is a professional module for hydraulic drive modeling and simulation in Simulink software. The simulation is based on the construction of near-real components, simulating the actual system to build a simulation block diagram, extending the capabilities of physical modeling and simulation in Simulink. The physical network control model with hydraulic and mechanical components established by this module is closer to reality, which can effectively improve the efficiency and accuracy of the design.

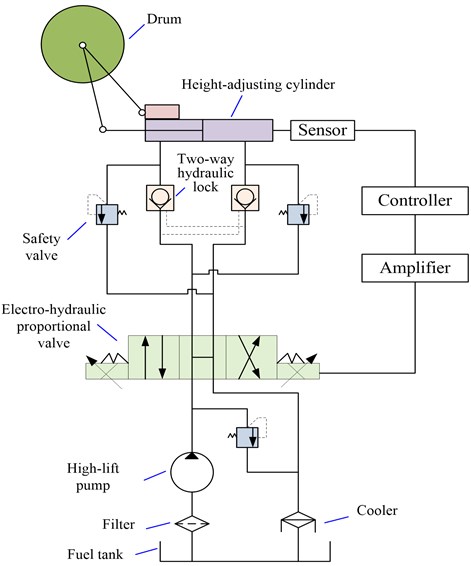
The Hydraulics Analog physical simulation model is constructed according to the selected parameters of the hydraulic system components and considering the nonlinear factors such as pipe connection, viscous damping, elastic load, external load, Coulomb friction and hydraulic oil source. Based on this model, the simulation model of the sliding mode controller is established according to the governing law of the system's transfer function and the design of the law of sliding mode control. The control model is shown in Fig. 3. The matrix $R={\left[\begin{array}{lll}{x}_p& {\dot{x}}_p& F_p\end{array}\right]}^T$, where, $F_p$ denotes the force of the cylinder piston. The logical structure of the approaching sliding mode controller is shown in Fig 4.

Fig. 3Simulation model of sliding mode control for height adjusting system of coal shearer

Fig. 4Logic structure diagram of sliding mode controller for reaching law

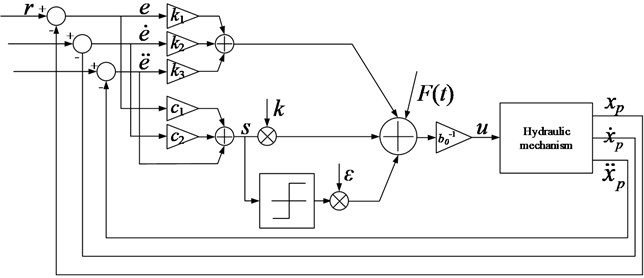
4.2. Simulation analysis

The controller steps sinusoidal signal and keeps track of the performance of the test, while the state of the system according to the equation, conventional PID controller simulation comparison.

The main simulation parameters are as follows: total leakage coefficient of hydraulic cylinder $C_{tp}=$1, flow coefficient $C_d=$0.7; hydraulic cylinder friction $F_f=$350 N; effective area of piston $A=$0.03 m²; oil modulus of elasticity ${\beta }_e=$800 MPa, oil density $\rho =$900 kg/m³, damping ratio ${\xi }_h=$0.2, natural frequency ${\omega }_h=$26 Hz; flow gain $K_q=$4, amplifier gain $K_a=$6, proportional valve gain $K_{sv}=$0.06, the total mass of the piston and load converted to the piston $m=$52 kg, damping coefficient of moving parts such as pistons and loads $B_p=$0.7N·s·m^-1, $K_p=$3.2, $K_i=$0.28, $K_d=$13.

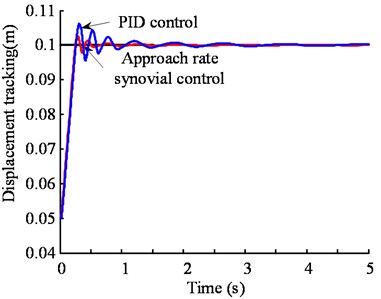
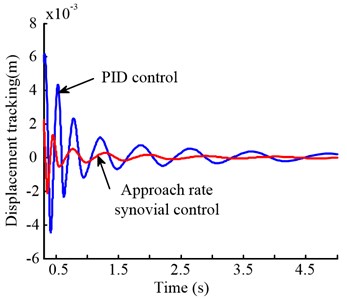
From Fig. 5(a) is a step signal tracking and Fig. 6(a) is error versus apparent, the process of tracking PID control system and the reaching law sliding mode control rise time is substantially the same, but the overshoot is 6 % under the PID control of the system, the oscillation frequency of the system is high and the oscillation amplitude is large, the system tends to be stable for a long time, and the error after the stability is larger than the target value; the overshoot of the system under sliding mode control is only 2.5 %. The oscillation frequency of the system is low and the oscillation amplitude is small, the system tends to be stable in a short period of time, and the error after the stabilization and the target value is also small. Therefore, the approaching sliding mode controller is superior to the traditional PID controller in terms of system speed, stability and accuracy. Hence, the sliding mode controller has better control effect.

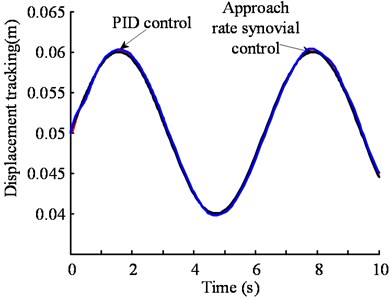
From Fig. 5(b) and Fig. 6(b) show that the tracking process approach system error than the sliding mode control law PID control error in the system to be smaller, and the initial oscillation amplitude is large under the PID control in system, the tracking error in the tracking process is large and the change is huge; the initial oscillation amplitude of the system under sliding mode control is small, and the tracking error in the tracking process is little and the change is small. It can also be seen from the tracking simulation of the sinusoidal signal that the control effect of the sliding mode controller is better and more ideal.

Fig. 5Comparison of PID control and sliding mode control tracking simulation in heightening system

a)

b)

Fig. 6Comparison of tracking error between PID control and sliding mode control in height adjustment system

a)

b)

Fig. 7Comparison of tracking simulation for adjusting system with external impact load

a) PID control

b) Approaching law sliding mode control

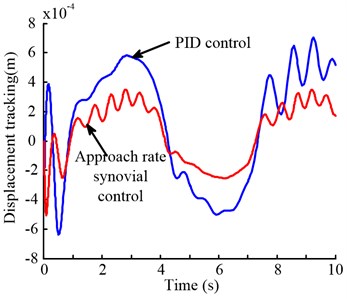
Fig. 7 shows the comparison of the control effects of the system when the system is under no load and subjected to different applied loads. The system is subjected to additional load shocks in 2-3 seconds. It can be seen from the figure that the system under PID control is obviously affected and the displacement output has a huge deviation, and the system is almost unaffected under the control of the sliding mode control. There is almost no deviation from the displacement output. Seen from the enlarged view, the PID control of the system when subjected to an impact load is the amount of displacement of the output variation rate of the system under the sliding mode control deviation rate of 7 times, sliding mode control system only occurs to 0.2 % deviation. Therefore, the near-law sliding mode controller can effectively overcome the disturbance impact on the external load, and has stronger adaptability to complex working conditions, and is especially suitable for the height control of the coal shearer under the harsh environment and the heavy load sudden working condition.

Fig. 8Output torque of cutting motor under different control methods

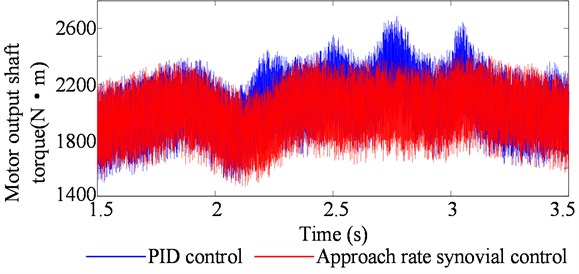
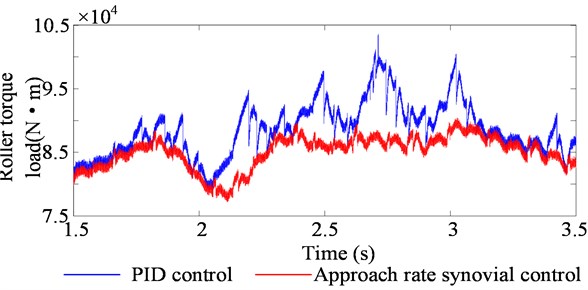
Fig. 8 and Fig. 9 show the change process of the output shaft torque and the drum torque load of the cutting motor when the drum is disturbed during the cutting process of the coal-rock interface. It can be seen from the figure that the drum height is more stable and accurate when it is controlled by the approaching law sliding mode. Therefore, the output shaft torque of the cutting motor and the drum load ratio are more stable and smaller when using the control of PID, and the cutting part of the coal shearer is cut. The drive system will have less impact and will help reducing damage to the various components of the drive train. Because the height of the drum controlled by the approaching law-sliding mode is almost unaffected by the disturbance of the external working conditions, and can still maintain the original trajectory operation, avoid cutting to the roof rock layer, reduce the load impact and the damage caused to the system. The control process is more stable. Under control of PID, the height of the drum cannot resist the external disturbance. The disturbance causes the drum height to change greatly, thus cutting the roof rock layer, increasing the system load and causing greater damage to the cutting section transmission system. Therefore, the drum height adjustment system is more suitable for adopting the law of sliding mode control, and its anti-disturbance ability is stronger. It not only can realize the fast, accurate and stable drum height control, but also help protect the coal shearer cutting system.

Fig. 9Drum torque load under different control methods

5.1. Study characteristics reaching law

Sliding mode control can not only improve the system's rapidity, stability and accuracy, but also as a nonlinear control method can effectively overcome the system uncertainty and external load disturbance impact through structural adjustment and change. But the sliding mode adopts the discontinuous control law makes the system need to switch back and forth between different control logic, which is easy to cause chattering unfavorable to the system and affecting its control effect. The chattering generated during the suppression control process have become the research hotspot of sliding mode control.

Fig. 10Comparison of control effects under different ε values

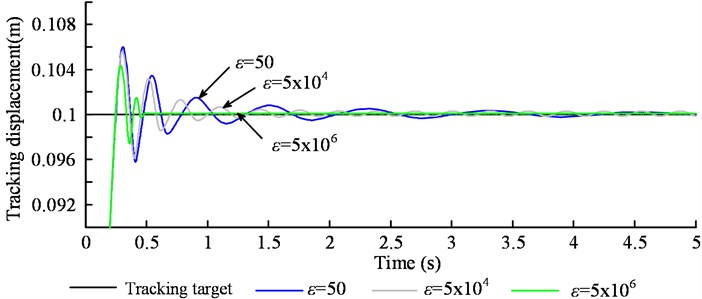
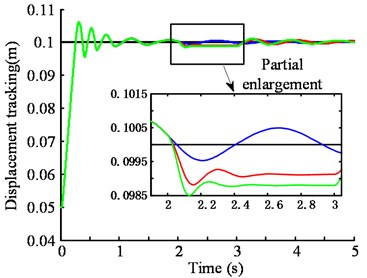
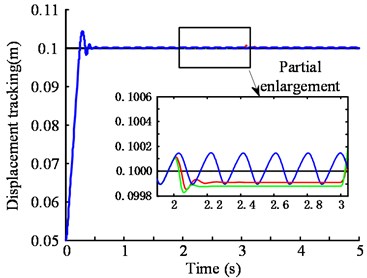
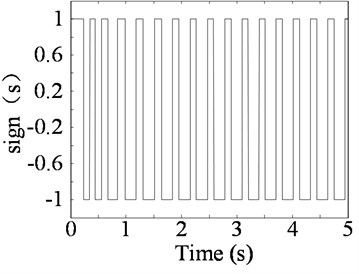
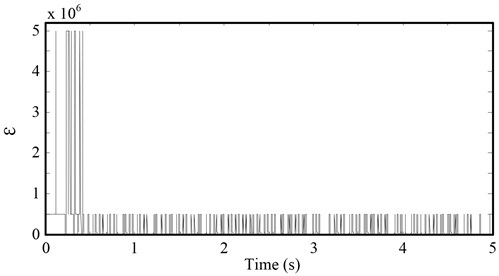
For the exponential approaching law sliding mode controller, the rapid selection of the approaching segment and the suppression of the chattering of the sliding segment can be ensured by the appropriate selection of the parameters $k$ and $\epsilon$. $k$ generally, takes a larger value to ensure a faster approach to the sliding surface, and the quality of the sliding mode is mainly affected by $\epsilon$. Fig. 10 shows the same parameters $k$, different parameters $\epsilon$ under control effect comparison chart, Fig. 11 is different parameters $\epsilon$ under control of the handover procedure function which characterizes the size of the system chattering. From Fig. 10 clear, the system has the smallest overshoot, and the error with the target value is the smallest and the precision is the highest when $\epsilon =$ 5×10⁶. But in Fig. 11(c), (d) can be seen the chattering situation is also the largest, which increases the energy consumption, affect the stability, increase the control difficult. In Fig. 10 can be seen, when $\epsilon =$50, the overshoot of the system is the largest, and the response speed of the system is also slow. It tends to be stable for a long time and is stable and has a large error with the target value. However, it can be seen from Fig. 11(a) that the chattering situation is the smallest. Therefore, the larger the $\epsilon$, the better the speed and accuracy of the system, but the greater the chattering situation, the more difficult the system is to control.

Fig. 11Different ε values under the sliding mode control process switching functions

a)$\epsilon =$50 partial enlargement

b)$\epsilon =$5×10⁴ partial enlargement

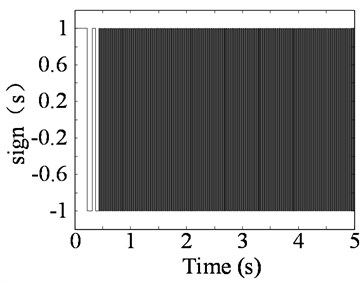
c)$\epsilon =$5×10⁶ partial enlargement

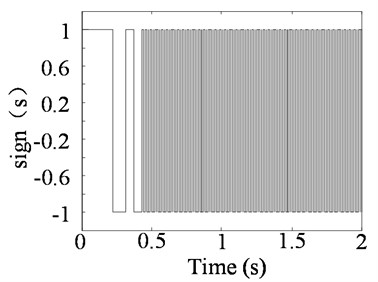
d)$\epsilon =$ 5×10⁶ partial enlargement

5.2. Variable speed reaching law based on fuzzy control

The law of the reach law obtained from Fig. 10 and Fig. 11 is known, in order to control sliding mode index reaching law chattering generated effectively suppressed, reaches the sliding surface $\epsilon$ value to be small. But at this time if $\left|s\right|$ smaller will extend the time that the moving point enters the sliding mode area, resulting in poor dynamic quality of the sliding mode motion. Increasing $\epsilon$ may be to accelerate the speed of approach, but larger ε increases the strength control system demand value. Conversely, decreasing ε means that the approach speed is reduced, and the motion point takes longer to enter the sliding mode region. Therefore, in the approaching process, when the system movement point is far away from the sliding surface, a strong control amount can be applied to ensure the approaching process is accelerated; the control amount is weakened when approaching or reaching the sliding surface, so as to reduce the chattering.

In other areas, the jitter sensitivity of a digital parameter adaptive tracking control system was studied by Michael Short in the way of using precise software-in-the-loop computational simulations, which presents some useful insights into the practical complexities when innovating adaptive real-time tracking control systems [19]. Therefore, in this paper an adaptive shifting approach law is designed to collect and calculate the distance and exit speed of the state track point from the sliding surface in real time, and select a reasonable control quantity to obtain better dynamic quality of sliding mode motion. In the engineering practice, the fixed parameter $k$ can be selected, and the method of dynamically adjusting the arrival speed ε can ensure the fastness of the approaching motion and the ability of the system to resist external disturbances, and effectively suppress the chattering of the system to ensure the steady-state accuracy.

Therefore, this paper will design a two-dimensional fuzzy optimization controller with two inputs and one output, with the switching function $s$ and its derivative $\dot{s}$ as the input quantity, and the fuzzy parameter optimization strategy with the arrival speed $\epsilon$ as the output, in order to realize the shifting of the moving point reaching rate. The basic rule is that when the moving point is far away from the sliding surface, a larger $\epsilon$ is taken, and when the moving point is closer to the sliding surface, a smaller $\epsilon$ is taken. The speed response is improved when the sliding mode is out of plane and the ability is raised of the system overcomes the perturbation and external interference. To soften the amount of control to eliminate chattering when the sliding surface is reached. And the control objective is to make the sliding mode switching function $s$ zero.

The fuzzy sets of the input and output of the fuzzy controller are:

Design the fuzzy rule table shown in Table 1.

5.3. Simulation analysis

Establishing sliding mode control model of variable speed reaching law based on Hydraulics Analog sliding mode control. the simulation results are shown in Fig. 10. From Figure understood, use of variable speed reaching law sliding mode control system having a less than $\epsilon =$50 at small reaching law control 33 % of small overshoot, fast response speed and can stabilize rapid after stabilization target value error is small, the response speed and precision with $\epsilon =$5×106 when a large reaching law control considerable. While in Fig. 13, Fig. 14 can be seen, the system of variable speed reaching law the chattering vibration is much smaller than that of the controller with large approach law, so the control effect of the variable speed reach sliding mode control is better than the sliding mode control under the fixed approaching law, which realizes the fastness and accuracy of the approaching motion. It also ensures the ability to resist external disturbances of the system and at the same time effectively suppresses the chattering of the system to achieve the purpose of ensuring steady-state accuracy, and is more suitable for the control of the height of the coal shearer drum.

Fig. 15 shows a reaching law sliding mode control under the shift ε change process, when the far point distance movement sliding surface has a large $\epsilon$, the movement distance point closes sliding surface has a smaller $\epsilon$. Thereby, the sliding mode control of the shifting approach law is realized.

Fig. 12Comparison of control effects under different approaches

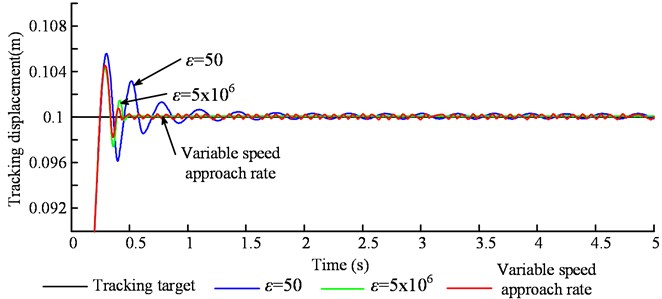
Fig. 13The sliding mode control function of the switching process when ε= 5×106

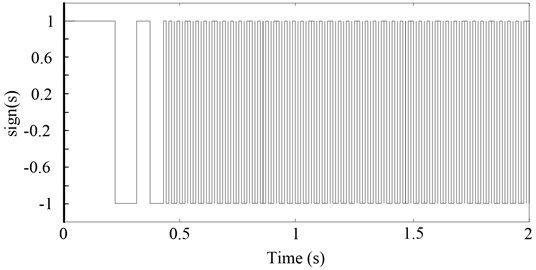
Fig. 14The sliding mode control process switching functions when ε= 50

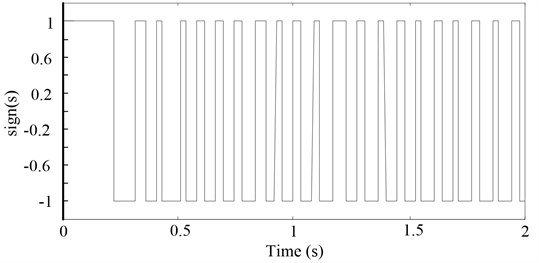
Fig. 15Shift reaching the sliding mode control law ε of change process