Fault diagnosis of rope tension in hoisting systems based on vibration signals

2.1. EEMD

The EMD method proposed by Huang can adaptively decompose a complex signal $x\left(t\right)$ into several IMFs $c_k\mathrm{}(k=\mathrm{1,2},...n)$ and a residue$r_n\text{,}$ then the signal is described as: $x\left(t\right)=\sum _{k=1}^n{c}_k\left(t\right)+r_n\left(t\right)$. However, the EMD method has the disadvantage of mode mixing. The EEMD method is proposed to overcome this problem, which is executed as follows:

1. Add white noise to the original signal.

2. Decompose the noise-added signal into IMFs by the EMD method.

3. Repeat steps 1-2 with different white noises each time.

4. Calculate the ensemble mean value of each IMF as the final IMF.

2.2. Permutation entropy

The PE was proposed by Bandt and Pompe to analyze the complexity of a time series. For a time series $\{x\left(j\right),j=\mathrm{1,2},...N\}$, the PE is calculated as the following steps.

1. Sequence reconstruction. The time series is converted into a multi-dimensional vector: $X\left(i\right)=\{x\left(i\right),x\left(i+\tau \right),...,x\left(i+\left(m-1\right)\tau \right)\}\text{,}$$i=\mathrm{1,2},...N-\left(m-1\right)\tau \text{,}$ where $m$ is the embedding dimension and $\tau$ is the delay factor.

2. Sorting. Each sequence in the embedding vector $X\left(i\right)$ is rearranged in ascending order as: $x\left(i+k_1\tau \right)\le x\left(i+k_2\tau \right)\le ...\le x\left(i+k_m\tau \right)$, and the rank is the permutation of the $X\left(i\right)$, marked as ${\pi }_{k_1,k_2,...,k_m}$.

3. Probability and entropy calculation. The relative frequency of the ${\pi }_k$ is calculated as:

The PE is defined as: $H_{PE}\left(m\right)=-\sum {\mathrm{}}_{k=1}^{m!}P\left({\pi }_k\right)\mathrm{l}\mathrm{n}P\left({\pi }_k\right)$.

The time lag $\tau$ and the embedding dimension $m$ are recommended to be 1 and 3-7, respectively [8].

2.3. PSO-SVM

SVM is a very useful technique for data classification and regression problems. The penalty parameter $c$ and the kernel parameter $g$ have a large influence in the SVM with Gaussian kernel. The PSO method is employed to optimize the parameters as follows [14]:

1. Initialize the particles ($c,g$) and the iterative time $N$.

2. Calculate the objective function value of the particle using the SVM training algorithm.

3. Calculate the optimal historical values of the individual and the population.

4. Update the particle velocity and position according to the speed and position update equations.

5. If the iterative time is satisfied, output the optimal parameters; otherwise, go back to step 3.

2.4. The proposed method to diagnose rope tension fault

The steps of the proposed method to diagnose rope tension faults are as follows:

1. Decompose the transverse vibration signal of the head sheave into IMFs by the EEMD.

2. Calculate the correlation coefficient between each IMF and the original signal; then extract the IMFs whose correlation coefficients are larger than a defined threshold as the main IMFs.

3. Calculate the energy and the PE of the main IMFs to create the feature vector.

4. Train the PSO-SVM model based on the vibration samples in different tension states.

5. Use the trained SVM model to diagnose the rope tension faults in practice.

3.1. Experiment setup

Tension states of a single rope contain overload, underload, and normal ones. The overload or underload faults may lead to a rope break or slack, respectively, which cause hoisting accidents. The experiment platform is a two-rope winding hoist with a height of 36 m, the schematic diagram of which is shown in Fig. 1. The experiment was performed on the two ropes of the right container. The vibration signals were obtained from the head sheave shafts because the noise and interference are small at the head sheave platform without power devices. The schematic diagram and photos of the data acquisition system are shown in Fig. 1 and Fig. 2, respectively. PCB vibration sensors were attached to the end faces of the head sheave shafts. Tension sensors were installed between the container and the two hoisting ropes. The vibration and tension signals were acquired by two NI cDAQ devices, respectively; then the data were transmitted to the laptop with LabVIEW software by wire and wireless communications, respectively. The sampling frequency was set 1024 Hz. The normal, overload, underload tension states of the rope were set to be 4900, 5600, 4200 N, respectively, by adjusting the weight of iron blocks in the container. 52 samples with a length of 1 s were obtained in each state, which is a small-sample problem as in engineering.

Fig. 1Schematic diagram of the experiment platform

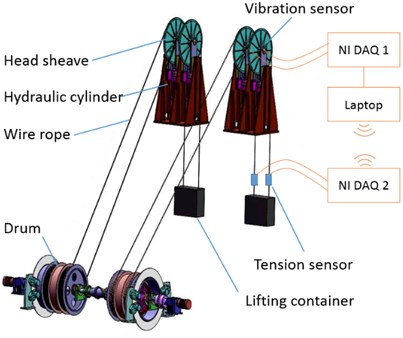
Fig. 2Photo of the data acquisition system

3.2. Processing

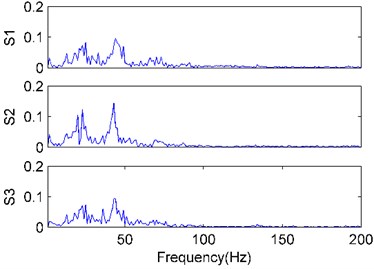
The vibration signal samples in the three states are shown in Fig. 3, in which S1, S2, and S3 are the overloaded, normal, and underloaded, respectively. The frequencies of the signals were obtained by the FFT, as shown in Fig. 4. It can be seen that the signals are complex and non-stationary, indicating it’s difficult to classify them based on the waves and the spectrums. That’s because the rope vibration has many natural frequencies, and a lot of interferences exist, such as wind.

Fig. 3The waves of the vibration signals

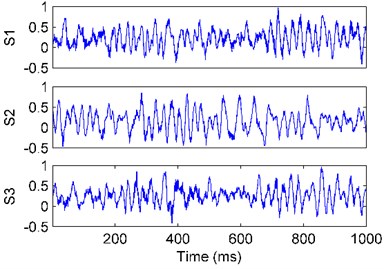
Fig. 4The FFT spectrums of the vibration signals

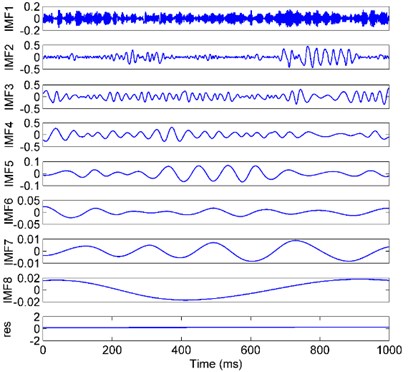
The signals were decomposed using the EEMD method, in which the amplitude of the added white noise was set to 0.2 times the standard deviation of the investigated signal, and the number of the ensembles was set to 50 [7]. The S2 sample was used as an example, shown in Fig. 5(a). As a comparison, the EMD is also applied, of which the result is shown in Fig. 5(b). The frequencies of the IMF 1-5 composed by the EEMD and EMD were shown in Fig. 6.

Fig. 5The decomposition results of the vibration signal

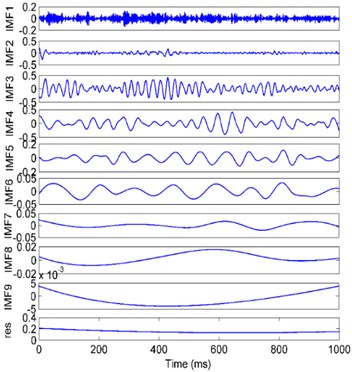
a) EEMD

b) EMD

It can be seen that the complicated signal is effectively decomposed into sample components from high frequency to low frequency by both the EMD and the EEMD. However, in the EEMD result, the frequency of each IMF is more concentrated, and the frequencies between adjacent IMFs are more separate, especially in IMF2 and IMF3. That means that the mode mixing was improved by the EEMD approach effectively.

The correlation coefficients between the IMFs and the original signal were calculated and the IMF 1-5 were selected to be the main IMFs with a threshold of 0.4. The PE and energy (EN) of the main IMFs were calculated to create the feature vector. 20 samples in each state were randomly selected to be the test samples. The “one-against-one” SVM was adopted for the multi-classification here. The PSO method was used to optimize the ($c,g$) parameters. The 5-fold cross-validation technique was used to improve the classification accuracy in the small sample problem. Other features and classifiers were also employed as comparisons.

Fig. 6The FFT spectrums of the decomposition results of the vibration signal

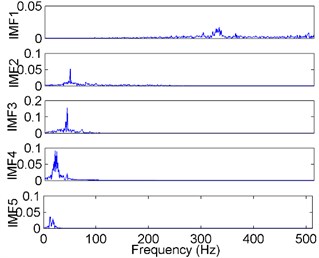
a) EEMD

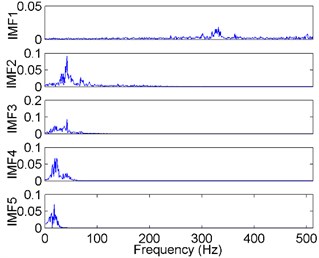
b) EMD

3.3. Results and discussions

The results of the accuracies with different decompositions, features and classifiers were shown in Table 1.

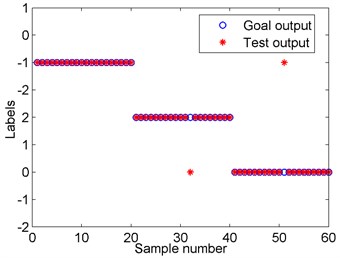
We can get the following information from the results: first, the multidimensional feature combining energy and entropy is more effective than a single feature by comparing 1-3. That’s because each feature has its advantage and multidimensional information is more comprehensive. Second, SVM has the lowest accuracy by comparing 3-5. The accuracy with different $\left(c,g\right)$ parameters is shown in Fig. 7, which means the parameters have great influence and indicates the necessity of the optimization. Third, the PSO-SVM performs better than other classifiers by comparing 3-6. Fourth, the EEMD has higher accuracy than the EMD by comparing 3, 7. All in all, the proposed method has the highest accuracy of 96.7 %, as shown in Fig. 8, which validates its effectiveness on the fault diagnosis of rope tension.

Fig. 7The influence of c, g parameters on accuracy

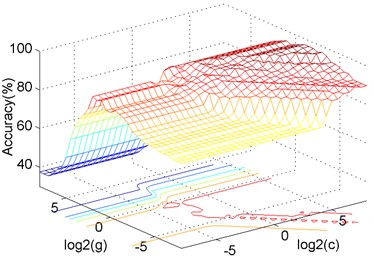
Fig. 8The result of the proposed method