A coupled volume-of-fluid and level set method in interDyMFoam solver

1. Introduction

The study of two-phase flow is very important because their various industrial applications. Their applications includes spray, lubrication and food stuff processing. Capturing the interface in incompressible two-phase flow is a challenging problem in computational fluid dynamics. The most popular methods for capturing the interface are the level set and volume-of-fluid. In the level set method [1], the signed distance function $\phi$ is used to describe the interface, where the value of $\phi$ is negative in the continuous phase, positive in the disperse phase and zero at the interface. Moreover, the level set function is smooth, giving an accurate curvature $\mathcal{k}$. The VOF [2] uses the volume fraction function $\alpha$ instead of the level set function. The volume fraction $\alpha$ takes the value of one in the dispersed phase and zero in the continuous phase. In addition, $\alpha$ is between zero and one in the cells that contain the interface. The VOF has a challenge in calculating the curvature $\mathcal{k}$ because the volume fraction function is discontinuous. On the other hand, the VOF is a mass conserving which is not the case in the level set method. In order to get an accurate calculation of the two-phase flow, a coupled VOF and LS method is used. In other words, the mass conservation in the VOF is combined with calculating $\mathcal{k}$ and other physical properties using the LS method. The interDyMFoam solver in OpenFOAM for 3D is modified to work with 2D planar and axisymmetric flows [3, 4]. The interDyMFoam for 2D is achieved to use the coupled VOF and LS method instead of using the VOF method only.

2. Main result

The solver interDyMFoam solves a two-phase flow problem for velocity $\mathbf{u}$, pressure $p$ and interface location. The continuity, momentum, and volume fraction equations are respectively given by:

where $\rho$ is the density, $\eta$ is the viscosity, $\dot{\gamma }=\nabla \mathbf{u}+(\nabla {\mathbf{u})}^T$ is the rate-of-strain tensor and $\mathbf{g}$ is the gravity. Moreover, ${\mathbf{F}}_{\sigma }=\sigma \mathcal{k}\mathbf{n}\delta$ represents the surface force tension, where $\sigma$ is the interfacial tension, $\mathbf{n}$ is the unit normal vector on the interface and $\delta$ is the Dirac delta function.

In the VOF, the density and viscosity are respectively calculated as $\rho \left(\alpha \right)=\alpha {\rho }_1+(1-\alpha ){\rho }_2$ and $\eta \left(\alpha \right)=\alpha {\eta }_1+(1-\alpha ){\eta }_2$ where the subscript represents the fluid phase. In the coupled VOF and LS method, only Eq. (3) is solved to find the volume fraction function. In addition, the LS function is initialized from the VOF function $\alpha$ as, ${\phi }_0=1.5\mathrm{\Delta }x(\alpha -0.5)$, where $\mathrm{\Delta }x$ is the mesh cell size. Note that the initial value is positive in the disperse phase and negative in the continuous phase. The next step is to solve the re-initialization equation to assign the LS function to a signed distance function:

where $\tau$ is the artificial time. The LS function at the beginning of the iterations is $\phi (x,0)={\phi }_0\left(x\right).$

The unit normal and the curvature are respectively computed using the LS function as, $\mathbf{n}=\nabla \phi /|\nabla \phi |$ and $\mathcal{k}=\nabla \bullet \mathbf{n}.$ Therefore, the surface tension force is computed using the LS method as, ${\mathbf{F}}_{\sigma }=\sigma \mathcal{k}\left(\phi \right)\mathbf{n}\delta \left(\phi \right),$ where $\delta \left(\phi \right)$ is defined as:

Also, the density and viscosity are calculated using the LS function as, $\rho \left(\phi \right)={\rho }_2+({\rho }_1-{\rho }_2)H\left(\phi \right)$ and $\eta \left(\phi \right)={\eta }_2+({\eta }_1-{\eta }_2)H\left(\phi \right)$, where $H$ is the Heaviside function and defined as:

The above equations are solved using the finite volume method (FVM). In FVM the computational domain is divided into a finite number of control volumes. Then, the equations are integrated over a control volume to get integral form of the equations. The integral equations are discretized using different methods to get the linear system of algebraic equations. In OpenFOAM, the dynamic mesh refinement works only for hexahedral cells. The boundary conditions for the LS equation are zeroGradient Which means that the derivative normal to the boundary is zero. For the other equations, there are several boundary conditions as zeroGradient and fixed value. For more details see [5].

3. Numerical test

The bubble rising in a column liquid is studied to compare the two solvers. The computational domain is a channel of length 1 m and hight 2 m. The bubble is a circle of radius 0.25 m and center (0.5, 0.5). The bubbles at time $t=$ 1 and $t=$ 2 s are shown in Figs. 1-2, where the bubbles on the left result from the interDyMFoam solver while the bubbles on the right result from the coupled interDyMFoam solver. The interface is smeared in the interDyMFoam solver. However, the coupled interDyMFoam gives a sharper interface.

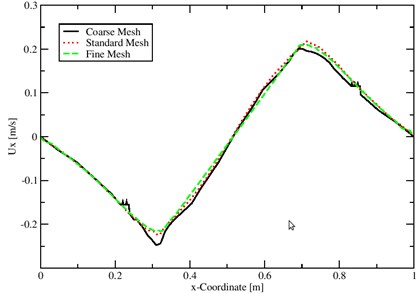
The velocity and pressure from coupled interDyMFoam for this 2D problem are compared along the horizontal line $y=$ 0 at time $t=$ 1 s. Fig. 4 shows the velocity graphs for the same case with three different meshes: coarse, standard, and fine mesh using the coupled interDyMFoam solver. The solutions are almost identical outside the bubble and behave similarly inside the bubble. Also, the graph show a zero velocity outside the bubble which is expected since the top and bottom walls are fixed. The velocity decreased before the bubble, increased inside the bubble, and then decreased after the bubble. Note that the graphs from the standard and fine meshes are almost identical which gives the convergence. Similarly, the pressure graph, Fig. 3, shows the same convergence. They have the same behavior overall, as the jump in pressure is decreasing by increasing the mesh resolution using coupled interDyMFoam solver. However, the solutions from coupled interDyMFoam solver are accurate even on the coarse mesh.

Fig. 1The bubble at time t= 1 s using a) interDyMFoam and b) coupled interDyMFoam

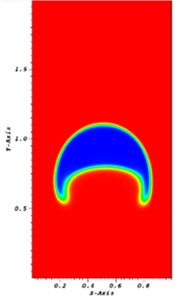
a)

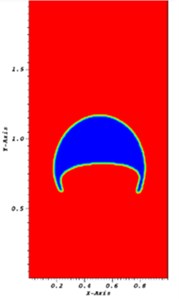
b)

Fig. 2The bubble at time t= 2 s using a) interDyMFoam and b) coupled interDyMFoam

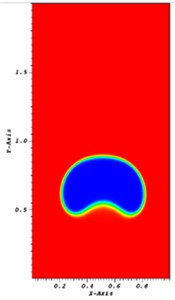
a)

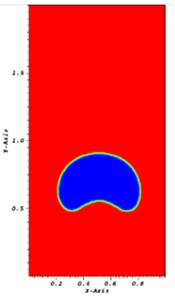
b)

Fig. 3Pressure on three different meshes using coupled interDyMFoam solver

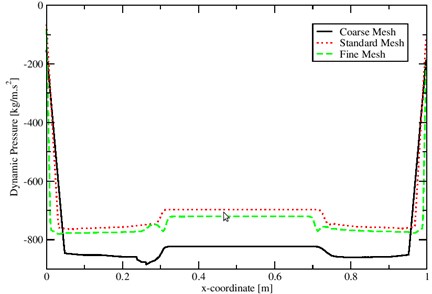
Fig. 4Velocity on three different meshes using coupled interDyMFoam solver

4. Conclusions

The interDyMFoam solver is modified to allow of using VOF and LS methods. The VOF is a mass conserving and the LS function is continuous to calculate the curvature. The modified solver is tested on the bubble rising in a liquid column. Moreover, the two solvers are compared on the same case test. The modified solver gives a sharper interface while the original solver smears the interface. Also, the convergence is obtained by comparing the pressure and velocity on three different meshes.