Coulomb crystal splitting effect in a linear electrodynamic trap

1. Introduction

Nowadays the processes of phase transitions in Coulomb structures localized in linear quadrupole traps are actively studied. This interest is caused by the potential applicability of the system “linear trap + linear ion crystal” as an elementary basis for quantum computing. At the same time, the existence of a restriction on the number of ions in the crystal when it keeps the linear structure, causes significant difficulties in implementing the described system in practice [1, 2]. There is a relationship between phase transitions and the form of effective potential, but this relationship has not been properly explored. The physical principle of splitting the effective potential and Coulomb crystal can be considered on the example of solving the three-dimensional localization problem.

One of the ion localization problems in three-dimensional space is the localization in a field of a linear ion trap with end cape electrodes. We consider a linear quadrupole trap field separately from the field of end cape electrodes, the potential energy of a charged ion $+q$ takes a form [3]:

where $q$ is an ion charge, $V_0$ is an amplitude of AC voltage applied to power “cylindrical” electrodes, $U_0$ is an amplitude of DC voltage applied to power “cylindrical” electrodes, $r_o-$ radius of the trap.

The potential energy does not depend on the axial coordinate $z$which describe the position of a localized particle along the power electrodes. Thus, movement along $z$ axis is unlimited, and we cannot talk about stable localization along this axis. To limit a motion of trapped object and border the localization area of the trap, end cape electrodes with constant positive potential are used [4, 5]. Fact that the end cape electrodes field has a minor effect on the localization process is usually taken as an axiom. However, this assertion is true only when the end cape electrodes voltage is much lower than the voltage at the power electrodes.

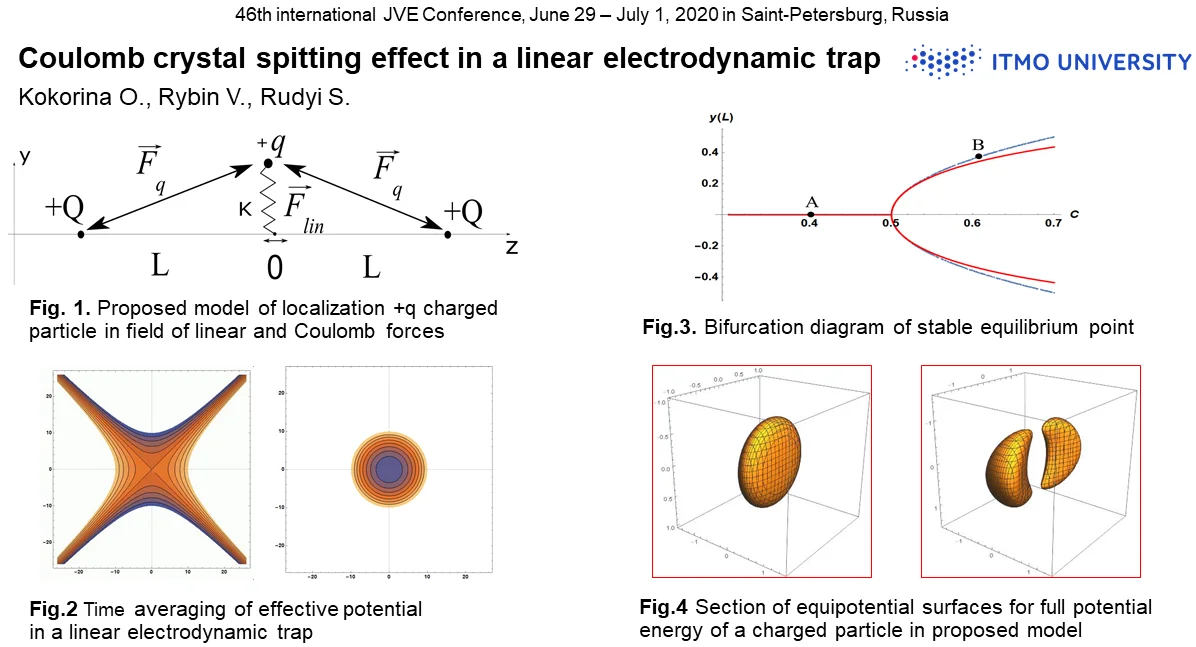
To describe the case of comparable voltages on end cape and power electrodes let us consider the following model: the point particle with a charge $+q$ is attached by a spring of stiffness $K$ to the $z$ axis, and the spring base can move along the axis $z$ freely (Fig. 1.) At a distance of $\pm L$ from the center of coordinates there are located two $+Q$ point charges. Determine stable equilibrium points of the $+q$charge in the present model.

Fig. 1Localization process of +q charge in field of linear and Coulomb forces

2. Analytical model

Defining the equilibrium points in the system consisting of two point charges $+Q$ located on the $z$ axis and a charged particle $+q$ which attached by a spring to the $z$ axis. The full particle potential energy will take a form:

To simplify the Eq. (2) we use the dimensionless coordinates $\tilde{y}=y/L\text{,}$$\tilde{z}=z/L\text{,}$$\tau =t\sqrt{K/m}$, as well as the parameter $C=kQq/2L^{3}K$. The equations of motion of particle are given by:

Equating the accelerations in the received equations to zero and find the potential minimum as pairs of ratios $(\tilde{z},\tilde{y})$. Considering that $C>$ 0, the solution of Eqs. (3-4) takes a following form:

Thus, when value $C$ is less than 1/2, the only stable equilibrium point is near the coordinate’s origin (0, 0). With increasing parameter $C$ ($C=$ 1/2 is the bifurcation point), a splitting of the stable position is observed. In this case, depending on the initial conditions, the point charge $+q$ is localized in one of the two new equilibrium positions with the coordinate $\left(0,\pm {\left[\left(2C-1\right)/3C\right]}^{1/2}\right)$ respectively.

The proposed model explains the potential splitting effect. Now let’s return to the localization in the linear ion trap Eq. (1). To describe the localization of a charged particle in a potential Eq. (1), it is often used the formalism of a time-independent effective potential. The equivalent effective potential in a quadrupole trap [6, 7] takes the form of:

where $m$ is the mass of an ion.

This effective potential Eq. (6) describes the oscillations in the harmonic oscillator in accordance with the proposed model. Field of the end cape electrodes can be represented as a potential distribution around two flat electrodes of round shape, located at a distance $L$ from the geometric center of the trap. Such field is a function of $L,r_E,R$, where $L$ and $r_E$ are the length and radius of the end cape electrodes, $R=\sqrt{x^2+y^2}$ [8].

The shape of the potential around flat end cape electrodes is much more complex than the shape of the point charge $+Q$ considered in the model. From the considered model we can notice the following concept: the field of the power electrodes makes no impact on axially particles movement along the trap, while the field of the end cape electrodes effects on axial and radial movement. This makes it possible to draw a parallel with the experiment. The full potential energy of a charged particle $+q$, considering the effective potential formalism and the effect of the end cape electrodes, will take the form of:

where $U_{-L}$, $U_{+L}$ are voltages on the end cape electrodes.

3. Results and discussion

As in the case with two charges $+Q\gg q$, with large value of DC voltage $U_{\pm L}$ on the end cape electrodes, splitting of the effective potential Eq. (7) is possible. Let us consider the section of equipotential surfaces of effective potential for a specific particle. The section of equipotential surfaces depends on the ratio of amplitudes of DC and AC voltage applied to the power electrodes, as well as the amplitudes of DC voltage on the locking electrodes.

Fig. 2Section of equipotential surfaces for potential energy U3x,y,z

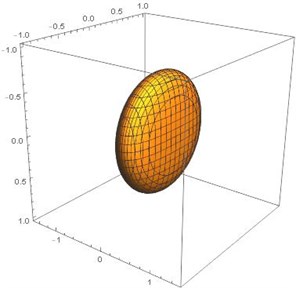
a)$U_{\pm L}\ll V$, $U_0=0$

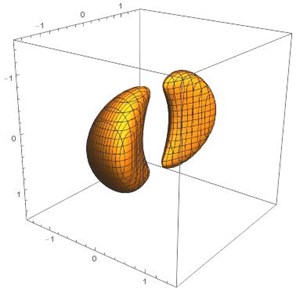
b)$U_{\pm L}\approx V$, $U_0=$ 0.1 V

Mathematical modeling of the effective potential gives an opportunity to observe the process of splitting the stability region in half as a result of increasing the potential of the end cap electrodes. At low value on the end cape electrodes $U_{\pm L}$, the transition from cylindrical to elliptical surfaces is observed. Elliptical surface is characterizing stable movement in three-dimensional space (Fig. 2(a)). With increase of voltage on end cape electrodes $U_{\pm L}$, we observe a splitting of stable equilibrium point. In the three-dimensional case, equipotential surfaces take double-well form ($U_0\ne 0$).

The observed transition in the form of the effective potential from a single-linked region (Fig. 2(a)) to two non-linked regions (Fig. 2(b)) corresponds to the Coulomb crystal splitting shown in [9]. In addition, in work [6] the formation of the additional equilibrium point with increasing voltage amplitude on the end cape electrodes is observed. The model proposed in this work describes the discovered splitting effect of effective potential at a ratio of amplitude of voltage on the end cape and power electrodes as 3:1. The displacement of the bifurcation point is caused by the trap geometry.

4. Conclusions

In this paper a simple model of ion localization was considered and mathematical modeling of the bifurcation process of stable equilibrium position was implemented. Thus, the model considered corresponds to the real localization of microparticles in electrodynamic traps. The considered model predicts the effect of splitting the Coulomb crystal in a quadrupole trap. This model of bifurcation of stable equilibrium position can be used to describe phase transitions in Coulomb crystals.