Design and simulation of shear-tension spring-type quasi-zero stiffness isolator

1. Introduction

The traditional linear vibration isolation technology can well solve the problem that the external excitation frequency is $\sqrt{2}$ times greater than the natural frequency of the system, but cannot meet the requirements for low frequency vibration isolation. The quasi-zero stiffness system can derive a stable zero stiffness interval at its equilibrium position, and guarantee certain load-bearing capacity of the system at the same time. Using such quasi-zero stiffness system, the low frequency vibration can be effectively isolated. In other word, the quasi-zero stiffness system can solve the contradiction between low frequency vibration isolation and bearing capacity.

In recent years, many scholars and experts at home and abroad have conducted in-depth investigations into the principles, applications, and expansion of the quasi-zero stiffness system [1-4]. Literature [5] studies a quasi-zero stiffness vibration isolation system consisting of a pair of inclined springs and a vertical spring, and analyzes static stability of the quasi-zero stiffness isolator. Literature [6] designs an adjustable quasi-zero stiffness isolator, and estimates the relationship between the system parameters. Literature [7] studies the parallel connection of Euler curved beam structure and linear vibration isolator with negative stiffness characteristics, and discuss the impact of excitation amplitude on the vibration isolation performance of the vibration isolator. Literature [8] proposes to use air springs to achieve quasi-zero stiffness characteristics, and the analysis of system dynamics indicates that its low-frequency vibration isolation performance is superior to that of linear vibration isolation system.

Based on above researches, this paper designs a quasi-zero stiffness isolator based on shear lever mechanism and tension spring, where the tension spring is used as a negative stiffness mechanism. Considering the insufficient capability of the system in isolation of the small-amplitude and low-frequency vibration, the shear lever mechanism is employed to increase participation degree of the negative stiffness mechanism. The vibration isolator is particularly suitable for low-frequency, ultra-low frequency vibration isolation, especially for small-amplitude, low-frequency vibration isolation. Compared with ordinary tie rod spring type isolator and compression spring type vibration isolator, the vibration isolator proposed in this work has a larger isolation interval for low frequency vibration and thus exhibits better performance in low-frequency vibration isolation.

2. Design of shear-tension spring type quasi-zero stiffness isolator

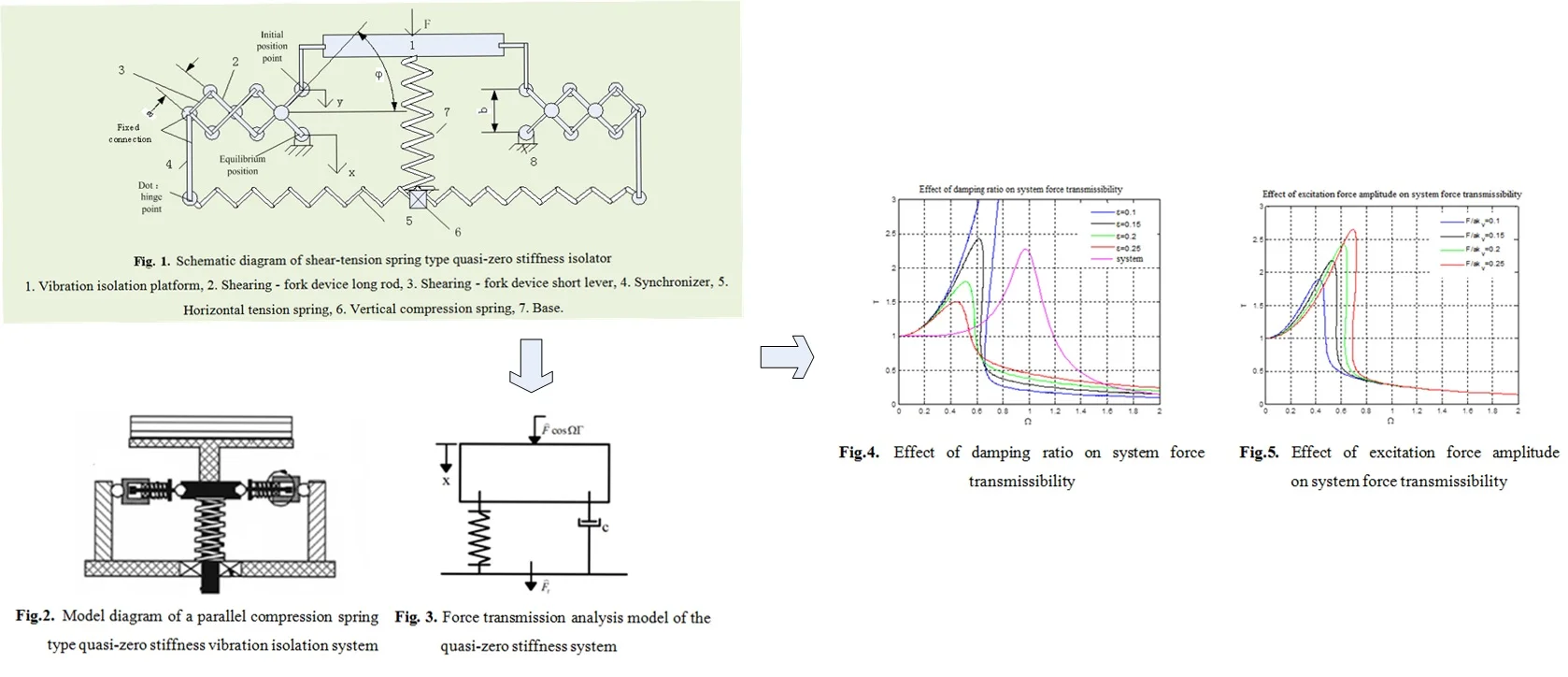
The shear-tension spring type quasi-zero stiffness isolator designed in this study is shown in Fig. 1. The elastic mechanism is composed of two tension springs and one compression spring, in which the two tension springs are placed horizontally and the one compression spring is placed vertically. The two ends of the vertical spring are connected to the carrier platform and the base, respectively. The two ends of the horizontal tension spring are respectively connected to the combined end of the two sets of shear lever mechanisms. The open end of the shear lever mechanism is connected to the carrier platform at one end and the base at the other end. The tension spring as a negative stiffness mechanism is connected in parallel to the positive stiffness mechanism generated by the vertical linear spring in the vertical direction. According to parallel principle of the elastic element and through appropriate adjustment of parameters, the mechanism can achieve quasi-zero stiffness of the system in the vertical direction.

Fig. 1Schematic diagram of shear-tension spring type quasi-zero stiffness isolator: 1. Vibration isolation platform, 2. Shearing – fork device long rod, 3. Shearing – fork device short lever, 4. Synchronizer, 5. Horizontal tension spring, 6. Vertical compression spring, 7. Base

In Fig. 1, the carrier platform has a side length of $L$, the short rod of the shear lever mechanism connected to the carrier platform has a length of a, and the long rod length is 2$a$, the horizontal tension spring connected to the shear lever mechanism has stiffness of $k_h$, and vertical spring connected to the base and the carrier platform has stiffness of $k_v$: The opening size of the shear lever mechanism (i.e. the length of the vertical spring) is adjustable to adapt to the vibration-isolated objects of different masses, so that the system maintains an equilibrium position and the system always shows quasi-zero stiffness. In the vibration isolation system state shown in the figure, the distance between the open ends of the shear lever mechanism is $b$, and the included angle is $2\phi$.

3. Comparison of shear lever isolator and compression spring isolator

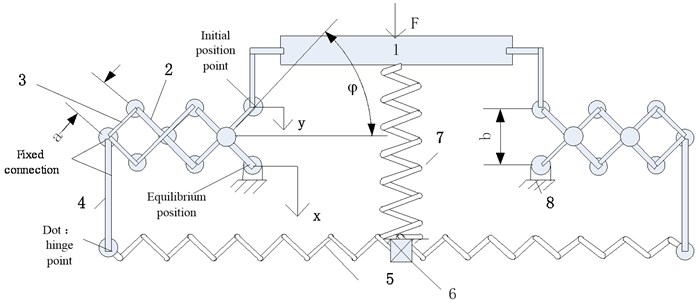
At present, compression spring is commonly adopted by most negative stiffness mechanism of parallel spring-type quasi-zero stiffness isolator [9]. As shown in Fig. 2, the knowledge of mechanical principle shows that compression spring is extremely prone to instability during operation, resulting in sharp decline in vibration isolation performance of the system [10]. To improve the stability of the vibration isolation system, a guide device is generally added in the compression spring, which will increase friction and damping of the system and thereby leading to higher difficulty in design of the vibration isolation system. To solve this problem, this paper proposes to use tension spring as the negative stiffness mechanism. The tension spring will not lose its stability while working and can ensure equivalent force value of the negative stiffness mechanism, thus comprehensively improving stability of the vibration isolation system and lowering design difficulty.

Fig. 2Model diagram of a parallel compression spring type quasi-zero stiffness vibration isolation system

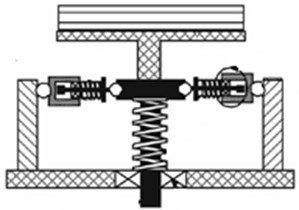
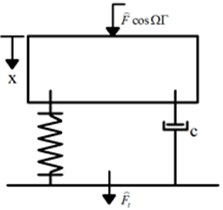
Fig. 3Force transmission analysis model of the quasi-zero stiffness system

3.2. Transmissibility

Harmonic balance method is used to solve motion equation of the nonlinear system. Let the solution of Eq. (1) be $\widehat{x}\left(\mathrm{\Gamma }\right)=A\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\Omega }\mathrm{\Gamma }+\theta \right)$, ignore its higher harmonic terms, eliminate the phase $\theta$, and substitute the solution into the motion Eq. (1) to obtain the amplitude-frequency characteristic equation of the system:

2

${\left(\frac{3}{4}\gamma A^3-A{\mathrm{\Omega }}^2\right)}^2+{\left(2\xi A\mathrm{\Omega }\right)}^2={\widehat{F}}^2,$

where $A$ is the system response amplitude, $\mathrm{\Omega }$ is the harmonic excitation frequency. The amplitude-frequency characteristic equation describes the relationship between the system response amplitude $A$ and the system parameter damping ratio $\xi$, stiffness ratio $\alpha$, excitation force amplitude $\widehat{F}$ as well as frequency $\mathrm{\Omega }$.

Vibration isolation of the system generally takes transmissibility as the evaluation standard. Let the force ${\widehat{f}}_t$ transmitted to the foundation through the system be:

3

${\widehat{f}}_t=2\xi \dot{\widehat{x}}+\gamma {\widehat{x}}^3.$

By harmonic balance method, the amplitude ${\widehat{F}}_t$ of the force transmitted to the foundation is solved:

4

${\widehat{F}}_t=\sqrt{{\left(\frac{3}{4}\gamma A^3\right)}^2+{\left(2\xi \mathrm{\Omega }A\right)}^2}.$

It can be seen from Eq. (4) that the magnitude of the force transmitted to the foundation is also related to the stiffness ratio $\alpha$, response amplitude $A$, damping ratio $\xi$, and excitation frequency $\mathrm{\Omega }$.Transmissibility is defined as the ratio of the amplitude of the force transmitted to the foundation to the amplitude of the excitation force. The force transmissibility of this system is:

5

$T=\frac{{\widehat{F}}_t}{\widehat{F}}=\sqrt{\frac{{\left(\frac{3}{4}\gamma A^3\right)}^2+{\left(2\xi \mathrm{\Omega }A\right)}^2}{{\widehat{F}}^2}}.$

It can be seen from the above formula that the magnitude of the force transmissibility $T$ of the system is related to the damping ratio $\xi$, stiffness ratio $\alpha$ and the magnitude of the excitation force amplitude $\widehat{F}$.

Fig. 4 shows the effect of damping ratio on the force transmissibility. It can be seen from Fig. 4 that change in damping ratio has a direct impact on the vibration isolation range and transmissibility. Specifically, when the damping ratio $\xi =\text{0.1}$, the curve bends to the right, the system shows a jump phenomenon, under such condition, the system exhibits a poor vibration isolation performance. When the damping ratio $\xi =\text{0.15}$, the vibration peak value is significantly reduced, the jump phenomenon is also significantly weakened, and the vibration isolation performance is greatly improved. When the damping ratio $\xi =\text{0.2}$, the jump phenomenon disappears and the initial vibration isolation frequency decreases, while the isolation capacity for high-frequency vibration decreases. It can be seen from the above analysis that as system damping ratio increases, the system jump phenomenon gradually weakens to zero, that is, the resonance peak completely disappears, and the damping ratio under such condition is referred to as the critical damping ratio. When the system damping ratio is greater than the critical damping ratio, the system will not show jumping phenomenon.

Fig. 4Effect of damping ratio on system force transmissibility

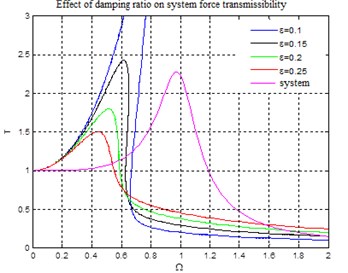
Fig. 5Effect of excitation force amplitude on system force transmissibility

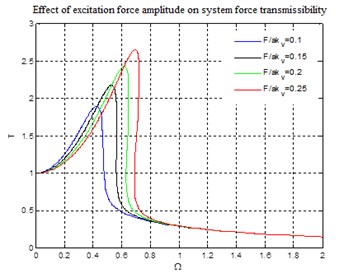
Fig. 5 shows the effect of excitation force amplitude on force transmissibility. It can be seen from Fig. 5 that the jump-up frequency and jump-down frequency of the system are positively correlated with the excitation force amplitude. For instance, the curve with excitation force amplitude at 0.25 has greater jump-up and jump-down frequencies, resulting in narrower frequency domain for vibration isolation and poor vibration isolation performance. Moreover, the corresponding force transmissibility is also significantly greater than transmissibility corresponding to the other three curves.

4. Conclusions

A linear compression spring as positive stiffness mechanism is connected in parallel with the tension spring as negative stiffness mechanism, and a shear lever mechanism is used to amplify the motion of the negative stiffness mechanism to form a shear-tension spring type quasi-zero stiffness vibration isolation system. The proposed system is suitable for low-frequency and ultra-low-frequency vibration isolation, especially for micro-amplitude and low-frequency vibration isolation.