A sensor fault diagnosis method based on KPCA and contribution graph

1. Introduction

The bridge health monitoring system can more comprehensively grasp the stress and damage evolution laws of the whole process of bridge structure construction and service and is one of the effective means to ensure the safety of the construction and service of large bridges [1]. At present, the three most common methods for sensor fault diagnosis are based on the analytical model, signal processing, and knowledge experience [2].

The multivariate statistical analysis method is a multivariate statistical process control method based on signal processing, which has been widely used in process performance monitoring and fault diagnosis [3]. The PCA (Principal Component Analysis) method is one of the most typical linear fault diagnosis methods [4]. However, the diagnostic performance is greatly reduced when it is applied to a non-linear system [5].

This paper proposes a new nonlinear diagnosis method based on the kernel principal component analysis (KPCA) and contribution graph. The KPCA method puts the measured data into a high-dimensional space through kernel function. In the high-dimensional space, the principal component is calculated by linear PCA method, $T^2$ and SPE statistics are constructed to detect whether the fault occurs or not, and then the contribution graph is drawn to locate the faulty sensor. Finally, numerical simulations are used to verify the superiority of the proposed KPCA combined with the contribution graph method in nonlinear sensor fault diagnosis than the traditional PCA method.

2. Sensor fault diagnosis method based on KPCA and contribution graph

3. Simulation analysis of numerical examples

First, the performance of the method proposed in this paper is verified by the simulation analysis of a nonlinear system with 7 sensors. The system is composed of seven equations of Eq. (6), which embodies four typical nonlinear relationships: polynomial nonlinearity (Eqs. (1-4)), exponential nonlinearity (Eq. (5)), trigonometric function nonlinearity (Eq. (6)) and inverse function nonlinearity (Eq. (7)):

Among them, $e_i\left(i=\mathrm{1,2},\cdots ,7\right)$ is Gaussian noise independent of each other, and all follow the normal distribution with a mean value of 0, and the variance is $0.1{\sigma }_i^2$, $\left(i=\mathrm{1,2},\cdots ,7\right)$; $y$ follows the uniform distribution in the interval [–1.5, 1.5]. Besides, there is a nonlinear relationship between $x_i$ and $y$, $x_i$ and $x_j$, $\left(i,j=\mathrm{1,2},\cdots ,7\right)$, and $i\ne j$. Suppose the system generates n sets of samples, then it forms a matrix $\mathbf{X}=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_7\right]$,$\left(i=\mathrm{1,2},\cdots ,7\right)$.

In order to compare the fault detection capabilities of KPCA and PCA for nonlinear systems, 1000 data samples are generated, and then the samples are normalized to a mean of 0 and a variance of 1, and then the data samples are trained and modeled by PCA and KPCA. The results show that the number of principal components of PCA is 2, thresholds $T_{\alpha }^2$and ${SPE}_{\alpha }$ are 9.26 and 1.90 respectively; the number of principal components of KPCA is 16, thresholds $T_{\alpha }^2$and ${SPE}_{\alpha }$ are 32.78 and 0.0001 respectively, the kernel function is Gaussian kernel function, and $C$ is 1.

Two types of sensor failures are analyzed below: (1) deviation failures that affect the average value; (2) gain failures that affect variance. Then three sets of 500 data test samples are generated. Among them, the first group of samples is the normal state inspection sample, which is used for the inspection under the normal state; the second group of samples is the fault 1 test sample, which is specially used to test the deviation fault, and the fixed deviation fault occurs in the manual setting ${\mathbf{x}}_4$ sensor and the deviation amplitude $b$ is 0.5${\sigma }_4$. The fault data is set according to Eq. (7):

The third group of samples is the fault 2 test sample, which is specially used to test the gain fault, and the sensor ${\mathbf{x}}_6$ is set to have a constant gain fault, the gain amplitude $G$ is 1.5. The fault data is set according to Eq. (8):

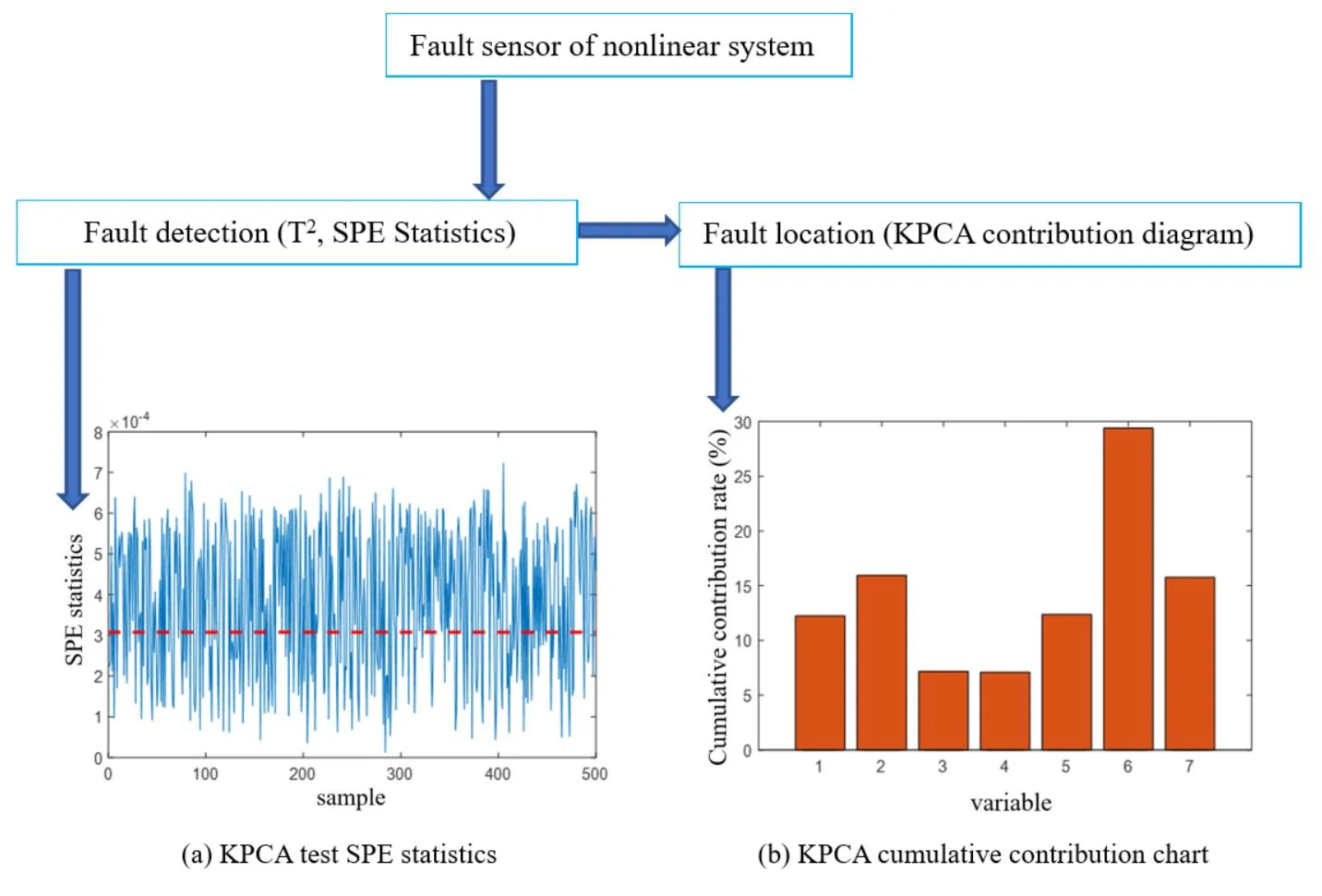
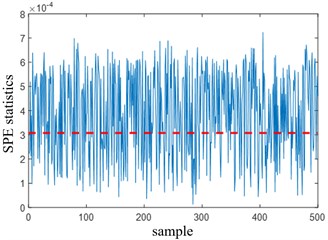
PCA and KPCA methods are used to diagnose normal samples. The PCA test results show that both $T^2$ and SPE statistics are out of limits, among which the $T^2$ and SPE statistics are out of limit rates of 3.6 % and 1.6 %, respectively, indicating that there is a misjudgment phenomenon when PCA is used for nonlinear system testing. The KPCA diagnosis result is shown in Fig. 1. The horizontal red dotted line in the figure represents the threshold of statistics. There is no obvious overrun of the statistics (the SPE statistics overrun rate is 0.8 %), and the $T^2$ statistics are all below 0.1, which is far below its threshold (the threshold is close to 10). It can be considered that the sensitivity of $T^2$ statistics to the identified faults is low, so SPE statistics are only used in subsequent fault diagnosis.

Fig. 1Statistical diagnosis result of the normal process

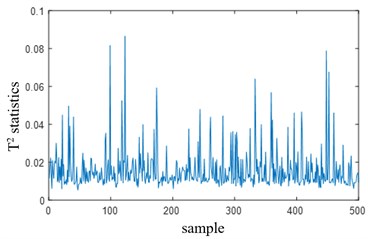
a) KPCA test T2 statistics

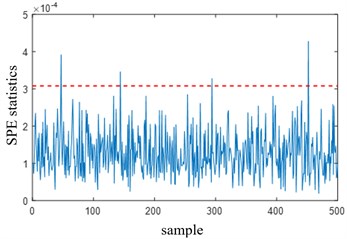
b) KPCA test SPE statistics

The PCA and KPCA methods are used to diagnose fault 1 sample. The PCA test results show that the overrun rate of PCA’s $T^2$ statistics is 4.4 %, and the overrun rate of SPE statistics is 3.8 %. The KPCA test results are shown in Fig. 2(a). The overrun rate of KPCA's SPE statistics is 84.8 %, which is far greater than the overrun rate of PCA, indicating that KPCA's ability to detect nonlinear sensor failure 1 is much better than PCA. Fig. 2(b) is a contribution diagram based on KPCA. From the figure, it can be found that the faulty sensor ${\mathbf{x}}_4$ has the largest cumulative contribution rate, which is consistent with the assumed faulty sensor, indicating that the positioning is accurate.

Fig. 2Diagnosis under fault 1

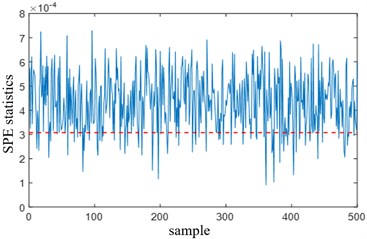
a) KPCA test SPE statistics

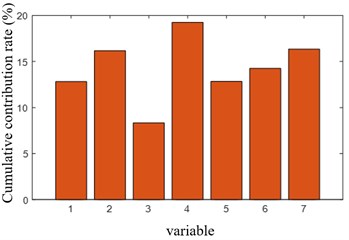
b) KPCA cumulative contribution chart

PCA and KPCA methods are used to diagnose 2 samples. PCA test results show that the overrun rates of $T^2$ and SPE statistics are 3.6 % and 0.8 % respectively; KPCA test results are shown in Fig. 3(a), in which the overrun rate of SPE statistics is 62.4 %, which is far greater than that of PCA, which also indicates that the ability of KPCA to detect nonlinear sensor fault 2 is far better than PCA. Then, the contribution graph based on KPCA in Fig. 3(b) shows that the fault sensor ${\mathbf{x}}_6$ with the largest cumulative contribution rate is the fault sensor introduced artificially before, indicating that the location is accurate.

In summary, the numerical simulation of a nonlinear system with 7 sensors mentioned in this paper shows that the sensor fault diagnosis method based on KPCA and contribution graph is accurate and effective, and it is significantly better than PCA’s nonlinear sensor fault diagnosis ability, so it is more suitable for fault diagnosis of nonlinear systems.

Fig. 3Diagnosis under fault 2

a) KPCA test SPE statistics

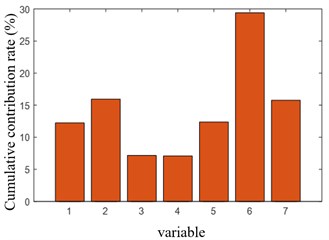
b) KPCA cumulative contribution chart

4. Conclusions

This paper proposes a sensor fault diagnosis method based on KPCA and contribution graph. It includes two parts: fault detection and fault location. The nonlinear sensor data in the original space is mapped to the linear high-dimensional feature space by the kernel function. PCA is used to calculate the principal component in the high-dimensional space, and T² and SPE statistics are constructed to detect the occurrence of sensor fault, and then the sensor fault location is completed by drawing a contribution graph. Numerical examples of nonlinear sensor faults show that the KPCA fault detection rate is much greater than that of PCA. So in the field of nonlinear fault diagnosis, the sensor fault diagnosis method based on KPCA and contribution graph proposed in this paper has a better diagnosis effect and application prospect than traditional PCA.