Regularized kernel function parameter of KPCA using WPSO-FDA for feature extraction and fault recognition of gearbox

2.1. Principle of KPCA

The idea of KPCA is to perform PCA in a high-dimensional feature space for acquiring more intrinsic information content of the original data [16], and it is described as follows.

Given a set of $l$ training samples ${\mathbf{x}}_1$, ${\mathbf{x}}_2$, ..., ${\mathbf{x}}_l$ in $R^N$ and a nonlinear mapping $\mathbf{\Phi }$: $R^N\to F$, $\mathbf{x}\to \mathbf{\Phi }\left(\mathbf{x}\right)$, assuming ${\sum }_{k=1}^l\mathbf{\Phi }\left({\mathbf{x}}_k\right)=$ 0, the following covariance matrix is given by:

and it can be found that eigenvalues $\lambda \ge$ 0 and eigenvectors $\mathbf{v}\in F\ne \left\{0\right\}$ satisfies $\lambda \mathbf{v}={\mathbf{C}}^{\mathbf{F}}\mathbf{v}$. Since all solutions $\mathbf{v}$ with $\lambda \ne$ 0 lie in the span of $\mathbf{\Phi }\left({\mathbf{x}}_1\right)$, ..., $\mathbf{\Phi }\left({\mathbf{x}}_l\right)$, there exist coefficients ${\alpha }_i$, $i=$ 1, 2, ..., $l$, such that:

Meanwhile, consider the equivalent equation:

Substituting Eqs. (1)-(2) into Eq. (3):

Define a $l\times l$ matrix $\mathbf{K}$ by $\mathbf{K}=\left(\mathbf{\Phi }\left({\mathbf{x}}_i\right)\cdot \mathbf{\Phi }\left({\mathbf{x}}_j\right)\right)=\left(\mathbf{K}\right({\mathbf{x}}_i,{\mathbf{x}}_j\left)\right)$ with $\mathbf{K}(\cdot ,\cdot )$ the Mercer kernel; the following compact form is:

where the squared matrix ${\mathbf{K}}^2$ denotes the product of $\mathbf{K}$ with itself. In the following, the following dual equivalent form can be:

Let ${\lambda }_{{}_1}^{*}\ge {\lambda }_{{}_2}^{*}\ge ...\ge {\lambda }_{{}_n}^{*}$ denote the eigenvalues of the matrix $\mathbf{K}$, that is ${\lambda }_i^{*}=l{\lambda }_i$, $i=$ 1, 2, ..., $l$ where ${\lambda }_i$ is the $i$th eigenvalue of the covariance matrix ${\mathbf{C}}^{\mathbf{F}}$. Thus Eq. (6) takes the standard form:

Eq. (7) is solved for nonzero eigenvalues ${\lambda }^{*}$ and coefficient eigenvectors $\mathbf{\alpha }$ and the solutions $\mathbf{\alpha }$ are normalized by requiring that the eigenvectors ${\mathbf{v}}^k$ of the covariance matrix ${\mathbf{C}}^{\mathbf{F}}$ are normalized to unit length, that is:

where it is assumed that the eigenvalues of $\mathbf{K}$ are arranged in decreasing order, with ${\lambda }_p$ being the corresponding smallest nonzero eigenvalue. Combining Eqs. (2) and (7), the normalization condition of Eq. (8) is equivalent to:

Finally, for the extraction of principal components, projections on eigenvectors ${\mathbf{v}}^k$: $k=$ 1, 2, ..., $p$ are computed in the feature space $F$ to acquire the principal components of input data by KPCA. Consequently, let $\mathbf{x}$ be a testing point with an image $\mathbf{\Phi }\left(\mathbf{x}\right)$ in $F$, then:

where ${\alpha }_{{}_i}^k$ is the $i$th coefficient of eigenvector ${\mathbf{\alpha }}_k$ associated with the $k$th eigenvalue of the matrix $\mathbf{K}$, and $t\left(k\right)$ is the $k$th extracted principal component.

2.2. Kernel parameter

KPCA is a kernel-based learning algorithm, it is crucial to choose an appropriate kernel because the geometric structure of the mapped samples is determined by the selected kernel and its parameters. By choosing different forms of kernel functions, KPCA can deal with many nonlinear problems [17, 18]. For kernel method, most of kernel functions researched currently mainly contain different features, such as polynomial kernel function, Radial Basis Function (RBF) kernel function and neural network kernel function. The choice of kernel function has an important influence on the results. Here RBF kernel function is taken as researched objective and it is defined by:

where the parameter $w$ is called width, and indicates the degree of smoothness of the function. The width must be varied very carefully. If $w$ is overestimated, the exponential tends to a linear behavior, and its projection in high-dimensional space loses its ability to separate non-linear data. On the contrary, when $w$ is underestimated, the result is highly sensitive to noise in the information of training. So, the choice of the appropriate function width $w$ is the result of a trade-off between the two, and a scientific method is required to guide through the selection process of the optimal value.

2.3. Establishment of the optimization model of kernel parameter by means of thought of FDA

The main advantage of KPCA stems from the mapping of input data into a high dimensional feature space, which may use linear algorithms despite of the nonlinearity in the original data. In pattern recognition, the idea of FDA is to find an optimal projection direction, along which the input data is projected into a straight line to distinguish better. That is to say, it can make intra class scatter as minimum as possible and the class space as much as possible. Therefore, an optimal method of kernel parameters based on the thought of FDA [19] can be proposed.

The mathematical model of kernel parameter based on Fisher norm is as follows.

Assume that two kinds of characteristic samples in a feature space are $X_1$($x_{11}$, $x_{12}$, …, $x_{1i}$), $X_2$($x_{21}$, $x_{22}$, …, $x_{2j}$), $i=$ 1, 2, 3,…, $n_1$, $j=$ 1, 2, 3, …, $n_2$.

The mean vectors of them are respectively as follows:

The square of the distance between classes is:

The square of the inner-class discrete degree $X_k$ is:

According to idea of FDA, the optimized objective function by PSO is set up [20]:

The minimal value of $f\left(w\right)$ can be solved to realize that the between-class scatter is the maximal whereas the within-class scatter is minimal. The parameter $w^{*}$ is set as the minimum point of Fisher discriminate function. Many experiments in references proved that for entirely non-linearly separable problem, the minimum point $w^{*}$ exists, while for linearly separable or almost linearly separable problem, the value of $f\left(w\right)$ is sharply decreased and then becomes steady with $w$ changing from the large to the little. At the same time the parameter $w$ can be $w^{*}$, and $f\left(w\right)$ can change to be steady in the end. For the multiclass problems, they can be transformed into two-class problems.

3.1. Principle of standard PSO

In the PSO algorithm, the process of searching for the best solution is imitating the movement and flocking of birds. Each particle stands for a potential solution which consists of a position and a velocity. At each iteration, the particle adjusts the velocity and position based on itself optimal location and the global optimal location in population. The equations WPSO are written as follows [8, 9]:

where $d$ is the dimension of search space, $n$ is the total number of particles, ${\mathbf{x}}_i=\left({\mathbf{x}}_{i1},\dots ,{\mathbf{x}}_{id}\right)$ and ${\mathbf{v}}_i=\left({\mathbf{v}}_{i1},\dots ,{\mathbf{v}}_{id}\right)$ denote the position and velocity of the particle, respectively; $p_{id}$ is current optimal position of the particle $i$, and $p_{gd}$ is whole population’s optimal position; $c_1$ and $c_2$ are acceleration constants with positive values, and usually set as 0-2; $r_1$ and $r_2$ are random numbers within the range [0 1]; $v_{id}$ is current flying velocity of the particle $i$ within the range $[-v_{max}\text{,}{v}_{max}]$, where $v_{max}$ is maximum particle velocity, being a non-negative number; $\omega$ is called inertia weight, which decreases linearly with the iteration:

where ${\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum and ${\omega }_{min}$ is the minimum of $\omega$, and typically, ${\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 0.9-1.4, ${\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}=$ 0.4, $t$ is current iteration number, and $T$ is the maximum number of iterations.

3.2. The steps optimized by WPSO-FDA for best solution

According to Eqs. (17) (18) and (19), the optimized steps and processes of the kernel parameter are as follows:

1) Calculate the square of the distance between the two classes $D_b$ and the square of intra-class scatter $D_{w1}$, $D_{w2}$ by Eqs. (14), (15) and (16);

2) Construct Fisher discriminate function $f\left(w\right)$ by Eq. (17), and regard it as a fitness for WPSO;

3) Give initial parameters such as the value range of the parameter $\omega$(${\omega }_{min}$, ${\omega }_{max}$), population size $m$ of WPSO, maximum iterative step $T$, constants $c_1$ and $c_2$, and maximum velocity limit $v_{\mathrm{m}\mathrm{a}\mathrm{x}}$;

4) Randomly create initial population $w$, then calculate the value of individual fitness $f_p$ of each particle and the global fitness value of the whole population $f_g$;

5) Carry out the particle’s velocity $v_{id}\left(t\right)$ and location $x_{id}\left(t\right)$ updating according to Eqs. (18) and (19);

6) Judge whether the termination condition of evolution is satisfied. If $t<T_{\mathrm{m}\mathrm{a}\mathrm{x}}$, steps (4)-(6) will be repeated until termination condition is satisfied. Or else, the current solution will be output as the optimal solution $w^{*}$, and the evolutionary computation is ended.

3.3. Simulation analysis of Iris data set by KPCA optimized by WPSO-FDA

The Iris data set is a typical test case for many statistical classification techniques, and it is selected in this paper as the test data for simulation analysis. In the data set, each group of data contains four properties of an Iris flower, i.e. sepal length, sepal width, petals length and petals width. Among three different types of flowers, the first and the other two types of flowers are linearly separable, but the latter two types of flower are nonlinear [20, 21]. 50 sets of data selected from each flower were used to simulation analysis. So, 150 groups of data from the three types of flowers can be divided into training set and test set, each containing 75 groups of data.

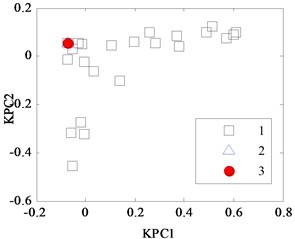
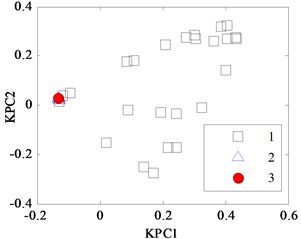
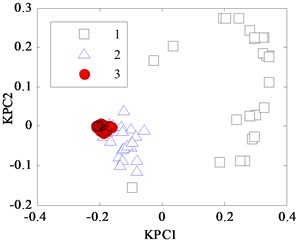
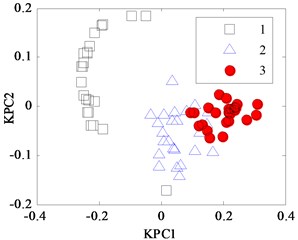
In the classification process of the Iris data by KPCA, it firstly maps the input vector into a high-dimensional feature space. Then, the mapping data in the feature space are analyzed, and their projections on the nonlinear principal component are obtained. This method firstly computes a vector in feature space called the first kernel principal component (KPC1) used to describe the maximum change direction of the data, and the second kernel principal component (KPC2) is orthogonal to the first principal component and describes the maximum of residual change direction. KPCA projections for Iris data with different kernel parameter width $w$ are shown in Fig. 1(a), (b), (c) and (d). When $w$ is too small, as shown in Fig. 1(a) and (b), where $w$ is set to 0.387 and 0.707, respectively, the projections appear “and” phenomenon, namely they have mixed together and cannot be separated into samples 2 and 3. In Fig. 1(c), when $w$ is 1.41, the latter two classes aliasing are less than that in Fig. 1(a) and (b), but it is still difficult to distinguish between them. In Fig. 1(d), when $w$ is 2.499, the output response range of the sample widens for the group, but there are some samples belonged to the 2nd type and the 3rd crossing together. So, it is necessary to optimize the regular parameter $w$ by WPSO-FDA.

According to the steps optimized by WPSO-FDA described in section 3.2, the kernel parameter $w$ has been searched, and its evolution curve is displayed in Fig. 2(a). The width $w$ achieves the optimized value $w^{*}$ as being 1.064 after iteration steps and the fitness function $f\left(w\right)$ becomes steady. Iris data set classification by KPCA with $w^{*}$ is displayed in Fig. 2(b). It can be seen that the three types flowers projections are in a different location, which is related to the three different categories.

Fig. 1KPCA projection diagram for Iris data with different width w

a)$w=$ 0.387

b)$w=$ 0.707

c)$w=$ 1.414

d)$w=$ 2.449

Fig. 2KPCA analysis results for Iris data

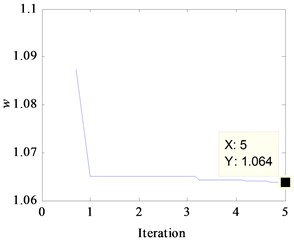
a) Kernel parameter $w$ evolution curve

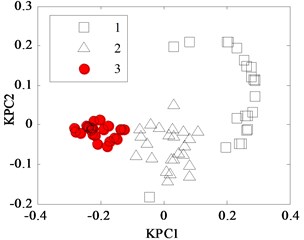
b) KPCA projection diagram, $w=$ 1.064

4.1. Fault simulation experiment of gearbox

The gearbox faults simulation experiment was carried out in the vibration lab of North University of China. The gearbox (JZQ-250 type) shown in Fig. 3 is composed of two pairs of gears, three shafts (input shaft, intermediate shaft and output shaft), three pairs of bearings and housing. Motor and magnetic powder brake are coupled with input shaft and output shaft, respectively. The experimental setup was composed of 36 channels dynamic signal data acquisition analysis system from Beijing Oriental Vibration Noise Institute, three-way accelerometer (piezoelectric), laptop computers, as shown in Fig. 4.

Fig. 3The gearbox fault diagnosis experimental system

Fig. 4The gearbox fault diagnosis test system

4.2. Faults of gearbox set up and its characteristic parameters

In the gearbox fault diagnosis experiment, the following simulation failures were set up besides normal working condition of gearbox: bearing outer ring crack, bearing cage fracture, gear broken tooth and gear broken tooth combined with bearing outer ring fracture. The three fault types are shown in Fig. 5.

Fig. 5The fault tested in the experiment

a) Gear broken tooth

b) Bearing cage fracture

c) Bearing outer ring crack

4.3. Vibration analysis of gearbox in different conditions

In this experiment, the input shaft speed was set to 1200 r/min, and the sampling frequency was 5120 Hz. Vibration signals of the normal working condition of the gearbox (A mode), bearing outer ring crack in intermediate shaft (B mode), bearing cage fracture (C mode), gear broken tooth (D mode), and gear broken tooth combined with bearing outer ring fracture (E mode) were acquired. The bearing characteristic frequencies of the five working states above are listed in Table 1 and include the rotating frequency of bearings mounted on three shafts, and the bearing theoretical failure frequency in every shaft are listed Table 2. The vibration signals under five conditions have been collected and processed. Their frequency spectrum curves are shown in Fig. 6, and their power spectrum density (PSD) curves are shown in Fig. 7.

Seen from Fig. 6(a)-(e), there are no big differences among the five frequency spectrum curves of vibration signal, and the amplitudes in characteristic frequencies are large, namely their vibrations are strong at this frequency. The frequency spectrum curves of B and C mode are very similar, so they cannot be used to differentiate between fault modes. In fact, the vibration signal on each measured point is not from a single component, which is the sum of different vibration signals from shafts, bearing and meshing gears in the gearbox. Therefore, it can be concluded that the curves only show the intrinsic characteristics of gearbox itself. From Fig. 7(a)-(e), the PSD curves in the case of failure are consistent with the frequency spectrum curves of the gearbox. Since the fault modes of gearbox cannot be determined to judge the gearbox fault status accurately only through the frequency curves, the further extraction of feature parameters in the time and frequency domain of vibration signals is required.

Fig. 6Frequency spectrum curves of vibration signals

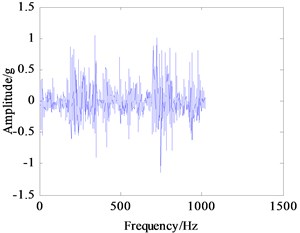
a) A mode

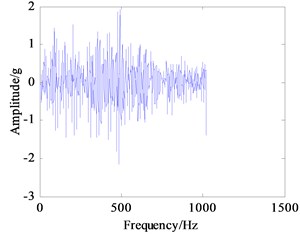
b) B mode

c) C mode

d) D mode

e) E mode

Fig. 7Power spectrum density curves of vibration signal

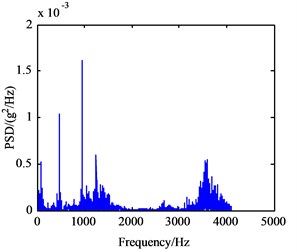
a) A mode

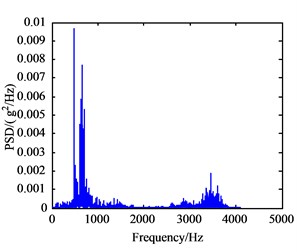
b) B mode

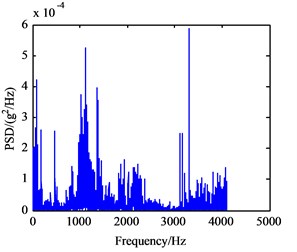
c) C mode

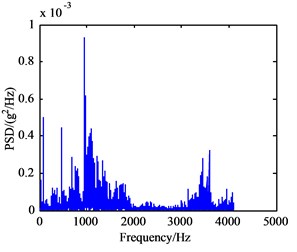
d) D mode

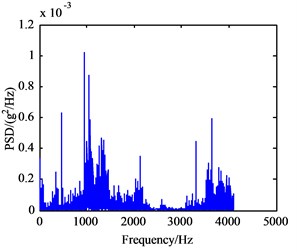
e) E mode

4.4. Construction of gearbox feature parameter set

The collected signals were processed, and in particular, the data of the measuring point 2 shown in Fig. 3 were analyzed. The original feature parameters set extracted from time domain and frequency domain are summarized in Table 3. The time-domain features include dimensional and dimensionless parameters, such as the mean value, skewness, kurtosis, waveform index and peak index. The frequency-domain features include only dimensional parameters such as frequency domain variance and correlation factor. 60 groups of feature samples were extracted under five working conditions, and half of them are training samples and the others are test samples. They were applied to KPCA for fault identification and classification of gearbox [24, 25].

5.1. Kernel parameters optimization based on WPSO-FDA

When KPCA is applied, the kernel parameter $w$ of the Radial Basis Function is a key to maintain good performance of nuclear study. Excessively large width $w$ will bring about the result that the influence spheres of a sample may be so large that irrelevant training samples will interfere the new test samples to make the right judgment; while too small value will result in the consequence that nuclear learning with only memory is unable to make a judgment to new sample [7]. Therefore, for training samples, kernel parameters optimization based on WPSO-FDA was conducted, and the parameter settings of WPSO are summarized in Table 4. The process of fitness function optimization with iteration under different conditions of gearbox is shown in Fig. 8. The width values $w^{*}$ of RBF between different fault states were obtained by WPSO-FDA optimization, and the optimization results are shown in Table 5. From Fig. 8 the width $w$ can be stabilized at an optimum value within the 50 iterations of fitness function evaluation. For example, for bearing outer ring crack and gear broken tooth, optimal parameter values $w^{*}$ can be stabilized at a width of 2.660. The optimal values are used in the parameters setting of KPCA for gearbox fault classification.

Fig. 8Fitness function evolution curves based on WPSO

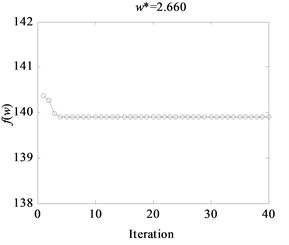
a) Bearing outer ring crack and gear broken tooth

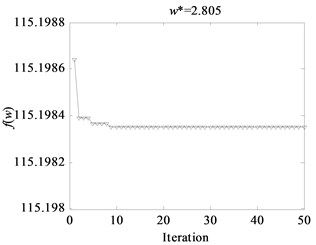
b) Bearing cage fracture and gear broken tooth combined with bearing outer ring crack

5.2. Fault classification of KPCA based on WPSO-FDA

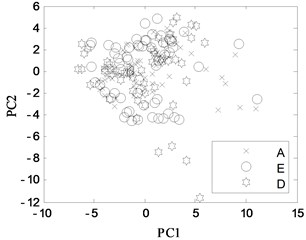
First, 30 groups of original feature sets drawn from normal condition were trained, then tests were carried through 30 groups of data from four fault modes such as bearing outer ring crack, bearing cage fracture, gear broken tooth and gear broken tooth combined with bearing outer ring fracture. Finally, for the same fault modes, the fault recognition results obtained by KPCA and PCA were analyzed, as shown in Fig. 9 and Fig. 10, respectively.

Fig. 9KPCA projection in different conditions

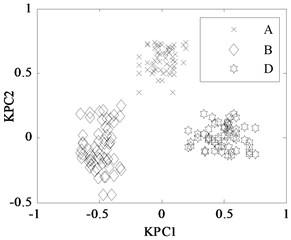
a) A, B, and D modes

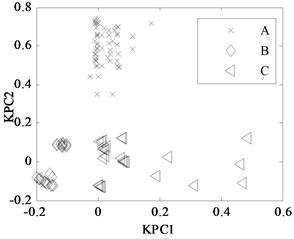
b) A, B, and C modes

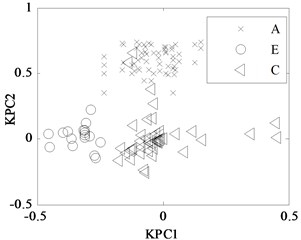
c) A, E and C modes

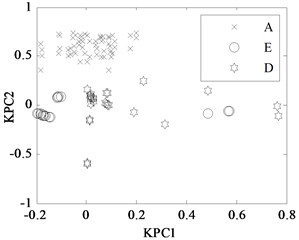
d) A, E and D modes

Fig. 10PCA projection in different conditions

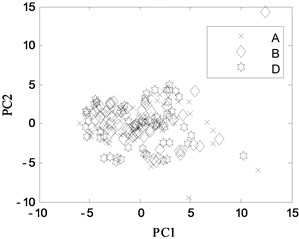
a) A, B and D modes

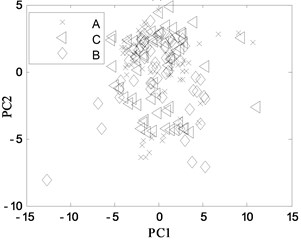
b) A, B and C modes

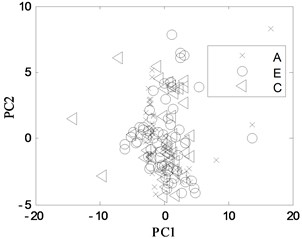
c) A, E and C modes

d) A, E and D modes

The KPCA projections from the first kernel principal component (KPC1) to the second kernel principal component (KPC2) in feature space are displayed in Fig. 9, and the PCA projections in original space are shown in Fig. 10. Observed from the Fig. 9, KPCA projections can clearly distinguish the various fault modes. The principal component projections from five modes conditions show obviously self-aggregation behaviours. Especially, the normal condition (A mode) can focus on a centre, while the bearing cage fracture (C mode) are relatively dispersed, but far from the normal cluster centre, apparently belong to different classes. From Fig. 9(c), there are a few crossing points between D mode and E mode, as a whole, the intra-class space of KPCA is little, whereas the space of different classes of KPCA is much. From Fig. 10, the PCA projections are mixed together, and normal condition cannot be clearly distinguished with the fault modes, and several faults cannot be separated from each other due to their nonlinearity. Therefore, the KPCA performance optimized by WPSO-FDA has obviously improved in the non-linear analysis, and accurately identifies not only single fault modes of gearbox but also the compound fault.