Study on simulation of wind load characteristics for photovoltaic generation systems

2.1. Physical geometry and mesh

In this paper, the photovoltaic power generation system consists of four PV panels, the PV panels are 0.05 m long, 2 m wide and 2 m thick. The model of the PV panels is shown in Fig. 1.

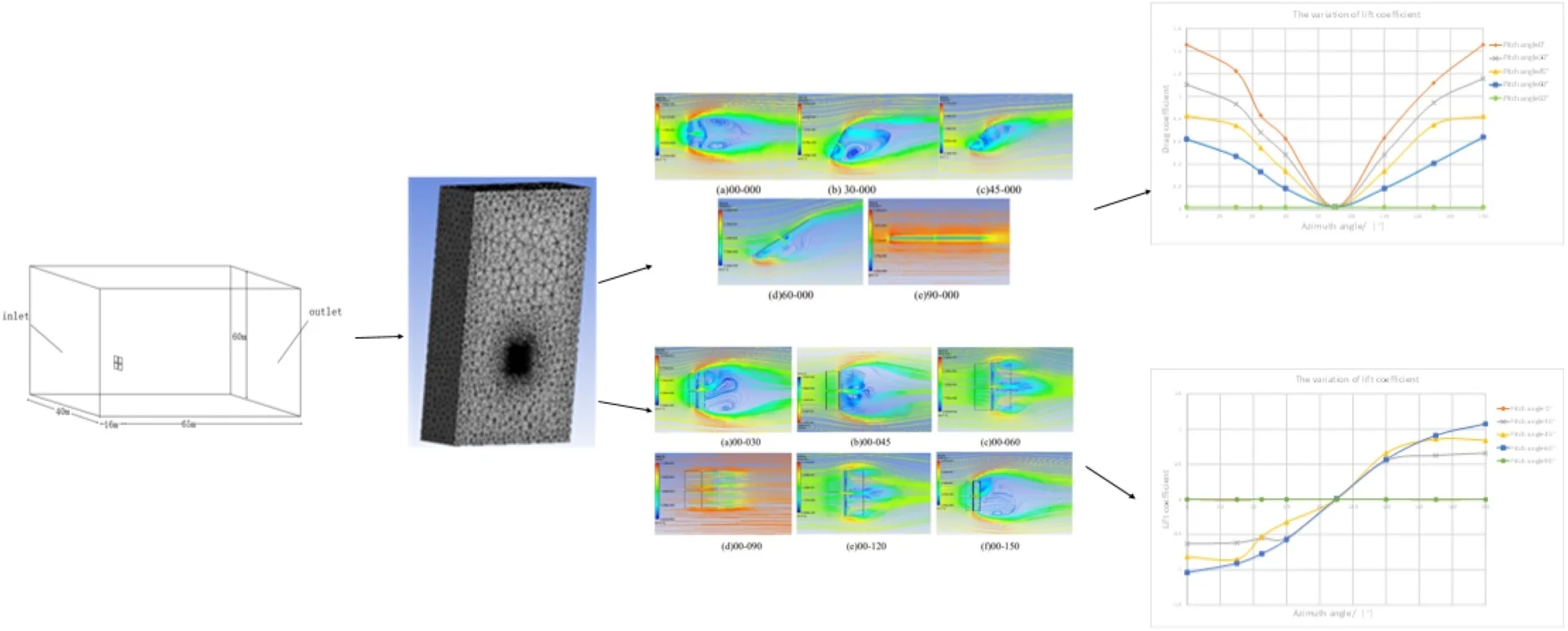
In order to ensure the full development of air in the fluid domain, the fluid domain should be large enough to ensure a certain distance between the boundary of the fluid domain and the PV panels, which can avoid the boundary of fluid domain to affect the reliability of simulation results. In order to judge better whether the size of the calculated field is reasonable, F. Baetke et al. proposed the concept of blocking rate $S$ [2]. When $S\le$ 3 %, the calculated field is considered to meet the requirement:

where $A_B$ is the effective windward area, $A_C$ is the cross-sectional area of the fluid domain. In this paper $A_B=$ 16 m², in order to ensure $S\le$ 3 %, $A_C\ge$ 533.4 m². The $L\times W\times H$ of the fluid domain selected based on experience are shown in Table 1.

The geometry of fluid domain is shown in Fig. 2.

Fig. 1Geometry of PV panels

Fig. 2Geometry of fluid domain

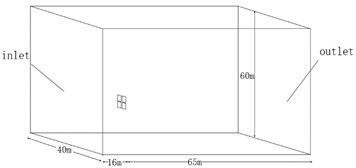
The geometry of fluid domain is imported into ANSYS Workbench and to be meshed, choosing mesh type as tetrahedron the generated mesh is shown in Fig. 3. The statistical result is that the number of nodes is 134932 and the number of elements is 740275. The average element quality is 0.84 > 0.8, which proves the element quality meets the requirement.

Fig. 3The mesh model of fluid domain

2.2. Boundary conditions and model settings

3.1. Characteristics of wind flow around PV panels

It is known that the photovoltaic power generation system can change automatically change the pitch angle and azimuth angle with the change of the sunlight. In this paper, the working conditions of the photovoltaic power generation system can be divided into 5×8 = 40 types. Using different codes to represent different working conditions of the PV panels, the coeds are shown as Table 2.

Firstly, the wind flow characteristics of PV panels with the same azimuth angle and different pitch angles are analyzed. The wind flow characteristics of PV plates with different angles are shown in Fig. 4 and Fig. 5.

Fig. 4Wind flow streamline in different pitch angles

a) 00-000

b) 30-000

c) 45-000

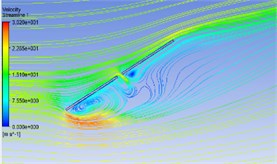
d) 60-000

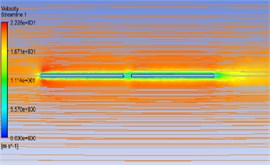
e) 90-000

Fig. 5Wind flow streamline in different azimuth angles

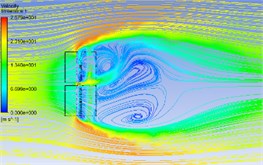
a) 00-030

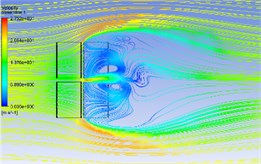
b) 00-045

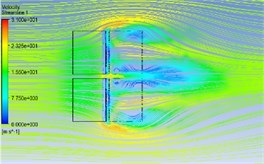
c) 00-060

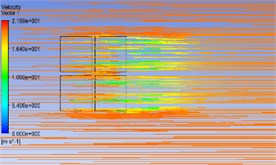
d) 00-090

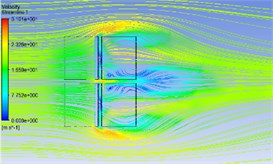
e) 00-120

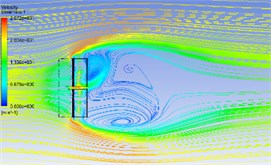
f) 00-150

The Fig. 4 shows the wind flow distribution at the $y=$ 19.6 m section of the PV panels with a pitch angle of 0° and different azimuth angles. The figure shows that in the 00-000 working condition the wind direction of the streamline vertical to the PV panels, the airflow will be blocked when it meets the PV panels, a variety of complex characteristics such as vortex shedding, backflow collision and airflow reattachment will occur on its edge and windward surface, so there are two symmetrical vortices on the back of a solar photovoltaic panel, and because of the gaps between the PV panels, the flow will form jets between the gaps, that is where the maximum wind speed will appear in the center gaps. The wind velocity between the bottom edge of the PV panels and the ground will increases due to “slit effect” which forms a large adverse pressure gradient specially in the condition of 30° pitch angle. With the increase of the pitch angle, the vortex scale and its influence range will decrease gradually. When the pitch angle increases 90°, the vortex has disappeared.

The Fig. 5 shows the wind flow distribution at the $y=$ 19.6 m section of the PV panels with azimuth angle of 0° and different pitch angles. The figure shows that in the 00-030 working condition as there are gaps between PV panels, three asymmetric vortices are formed on the back of PV panels; one of the vortex is formed on the jet flow due to its fast speed, and two vortices are formed on the edges of the panels due to the "slit effect". When the azimuth angle is 60°, 90° and 120°, the wind flow in these azimuth conditions does not separate after obvious airflow impact at the windward front due to the significant reduction of the windward area. The average wind speed distribution is relatively gentle. The vortex distribution in the 00-150 condition is similar to that in the 00-030 condition.

3.2. The variation of wind coefficient of PV panels

The lift force and the drag force can be obtained through FLUENT numerical simulation. The lift force and the drag force are two main factors that will influence the strength of the PV panels.

Wind force $F$ is related to fluid density $\rho$, wind speed $v$, fluid viscosity $\mu$ and feature sizes $D$, the function expression can be written as follows:

where $D^2$ is proportional to the area, $Re=\rho vD/\mu$ is Reynolds number, $C_F=f\left(Re\right)$, $C_F$ is wind coefficient [5]:

where $i\mathrm{}$represents the direction of the wind force. In this paper $C_z$ is the drag coefficient, $C_y$ is the lift coefficient. The variation of drag coefficient and lift coefficient with the pitch angle and azimuth angle of the PV panel is shown in Fig. 5.

Fig. 6The variation of wind coefficient with the pitch angle and azimuth angle

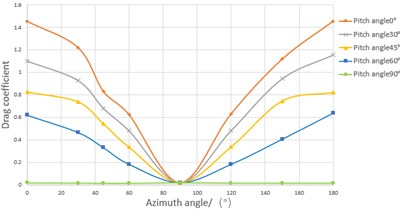
a)

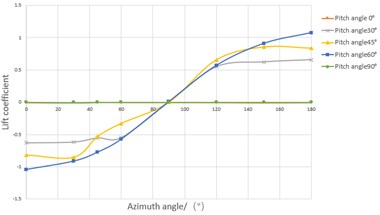
b)

It can be seen from the figure that the drag coefficient presents an approximately symmetric distribution. The drag coefficient decreases gradually with the increase of azimuth angle when azimuth angle between 0° to 90° then increases gradually with the increase of azimuth angle when azimuth angle between 90° to 180°. The variation of lift coefficient at different azimuth angles is complicated. When the pitch angle is 0° and 90°, the lift coefficient doesn’t change significantly with the azimuth angle, and the lift coefficient is close to 0. When the pitch angle is 30°, 45° and 60°, the lift coefficient increases with the increase of azimuth angle when the azimuth angle between 0° to 90°. When the azimuth angle is greater than 90°, the sign of the lift coefficient changes that means the direction of lift force has been changed.

The results show that when the effective windward area decreases, the drag coefficient of photovoltaic panels will be decreased. Therefore, when the wind speed is too high, the drag force can be reduced by changing azimuth angle and pitch angle. It can be seen the lift coefficient and the drag coefficient are smallest in the 90-090 condition.