Curved water flow characteristics and its influence on navigation

1. Introduction

Because of the complexity of the flow state in the curve channel, it is difficult to control the navigation state of the ship in fairway. Therefore, a specific method is needed to realize the movement state of the bend flow. The actual ship test cost is expensive, the fund is limited to realize. Therefore, this paper uses FLUENT software to simulate the movement state of curved river [1].

Fluent is the most popular commercial CFD software package in the world, with a 60 % market share in the United States. Fluent can be used in industries related to fluids, heat transfer and chemical reactions. It has a wealth of physical models, advanced numerical methods and powerful pre- and post-processing functions. It has a wide range of applications in aerospace, automotive design, oil and gas and turbine design.

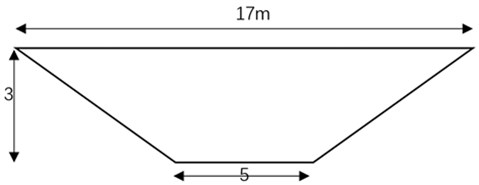
In this simulation, for the purpose of differential comparative analysis, three sections of the curved rivers were simulated. The degrees of the curved rivers were 60°, 90° and 120° (as shown in Fig. 1). In this numerical simulation, the cross section of the river channel is trapezoidal, and the cross section does not change with the bend (as shown in Fig. 2). The river bottom is 5 m wide, the river surface is 17 m wide, the channel height is 3 m, and the slope is a 1:2 slope. The straight length of the entrance is 45 m, and the straight length of the exit of the curve is 35 m.

Boundary condition setting: the inlet water velocity is 2 m/s, the roughness coefficient of the river bed and the river wall is 0.2.

Fig. 1Planar model of the curve

Fig. 2Cross section of the curve

2. Simulation model

The FLUENT RNG $k$~$\epsilon$ model is often used for numerical simulation of pipeline flow and river flow. The model has the advantages of high accuracy and stability [2]. There are four sets of control amplifiers for this model, as shown below:

Continuity equation:

Momentum equation:

$k$–equation:

$\epsilon$-equation:

where $x_i$ (= $x$, $y$) represents respectively the vertical and vertical coordinates; $u_i$ (= $u_x$, $u_y$) represents respectively $x$ axis velocity and $y$ axis velocity of flow, res; $\rho$ represents water density; $p$ represents pressure; $\nu$ represents the kinematics viscosity; ${\nu }_t$ represents viscosity of eddy and it can be expressed by ${\nu }_t=C_{\mu }\left(k^2/\epsilon \right)$, where $k$ represents the kinetic energy of turbulence, $\epsilon$ represents $k$ dissipation rate and $C_{\mu }$is 0.085. The other parameters are: $C_1^{\mathrm{*}}=C_1-\frac{\eta (1-\eta /{\eta }_0)}{1+\lambda {\eta }^3}$, $\eta =\frac{Sk}{\epsilon }$, $S=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$, $C_1=$ 1.42, ${\eta }_o=$ 4.377, $\lambda =$ 0.012, $G_k=\rho {\nu }_t\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\frac{\partial u_i}{\partial x_j}$, $C_2=$ 1.68 and ${\alpha }_k={\alpha }_{\epsilon }=$ 1.39. The calculation boundary conditions can be treated according to the following: the turbulent kinetic energy $k_{in}$ and the turbulent dissipation rate ${\epsilon }_{in}$ in the inflow boundary are expressed are [3-4]:

In which $u_{in}$ represents the inflow boundary average velocity, $D$ represents channel width. In the outflow boundary the flow is treated as developed fully [5]. The second-order upwind scheme is used for simulation. Mesh adaptively adjusting is used.

3. The characteristics of circulation current

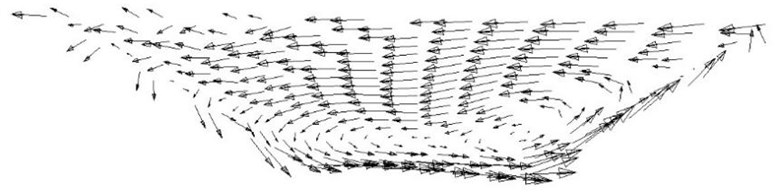
According to the simulation, the conclusion can be known: as the degree of the curved river increases, the strength of the circulation current and turbulence increases [3]. The bottom current of the circulation in the bend flows to the convex bank and the surface current flows to the concave bank. The velocity and flow direction of the circulation in the bend vary with the water depth. Therefore, the circulation in the bend has different effects on the ships with different draughts. The circulation current and turbulence in curved channel can result in the following effects on ship’s navigation:1) The circulation current of the curve causes the yaw between the ship and the planned route, so the ship needs to use the rudder to correct the course in order to ensure that the ship is on the planned route; 2) In order to ensure the safety of navigation, the width of channel must be increased because of the ship’s yaw; 3)Special care must be taken to avoid collision, grounding and reef accidents caused by ship’s yaw.

Fig. 3Circulation current of the 60° bend

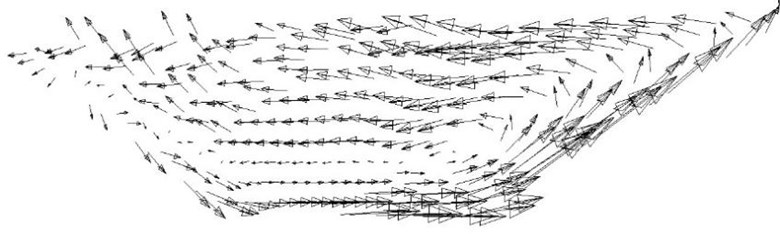
Fig. 4Circulation current of the 90° bend

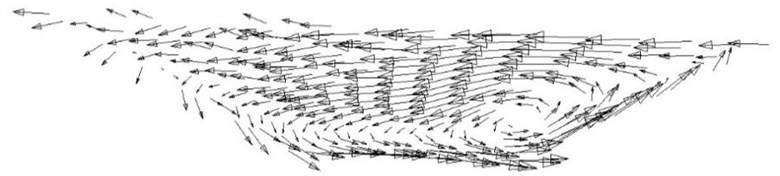
Fig. 5Circulation current of the 120° bend

4. Strategy of the safe navigation

(1) When the ship is driving in a curve, it should continuously adjust the movement state of the ship according to the water flow in response to turbulence.

The water flows in the bends are squeezed against each other, causing the water flow to be cluttered. When the ship is driving here, the force across the ship is uneven, which makes it difficult for the ship to control and deviate from the channel. During the voyage, the direction of the route should be pointed out, the ship should be adjusted so as not to deviate from the channel, and the ship should be driven safely [4].

(2) When the degree of curved rivers is larger, the circulation is greater, and the direction of movement of the ship is adjusted to reduce the amount of flow-induced drift. According to the simulation, the greater the bending degree of the channel, the greater the strength of the circulation in the curve, and the ship was easier affected. The ship should point in the direction of the convex bank as much as possible to reduce the amount of flow-induced drift [5].

5. Width allowance in curved channel

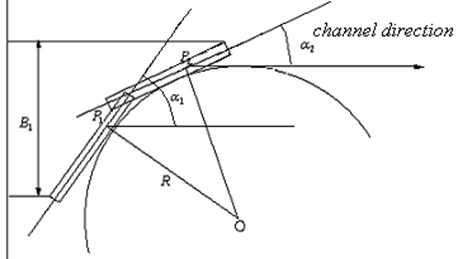
When a ship passes through a curved course, it was affected by circulation; a certain amount of flow-induced drift will be generated. At the same time, as the strength of the circulation increases, the flow-induced drift increases, and a larger width is required. Therefore, it is necessary to rationally design the width of the curved channel according to the actual situation. Ship passes a curved channel is shown in Fig. 6.

In order to ensure ship navigates in curved fairway always, ship must alter course by using rudder frequently, so there exists kicks in the course of altering course, so there must set apart some space to meet kicks requirements. Each parameter in Fig. 6 indicates the following meaning: $a_1$ is the initial course angle when the vessel is navigated into the winding channel; $a_2$ is the course angle when the vessel is navigated out of the winding channel; $R$ is the radius of the curvature of the winding channel. According to Fig. 6, width allowance $B_1$ in curved channel can be expressed as following:

(1) When ${\alpha }_1>$ 0 and ${\alpha }_2\ge$ 0:

(2) When ${\alpha }_1>$ 0 and 0 $\ge {\alpha }_2\ge -{\alpha }_1$:

In the above two formulas: $b$ is ship’s breadth; $L$ is ship’s length; $P$ is the distance from the ship turning center to the ship astern.

Fig. 6Ship’s navigation in curved channel

6. Conclusions

In this paper, through the numerical simulation of Fluent software, it is concluded that the more the bend, the greater the circulation intensity. According to the conclusions, the safety countermeasures when the ship is driving in the curve are given. Reduce the probability of a ship’s accident in a curve, and ensure the safety of the crew's life and property.