Abstract
This paper uses a steel engine hood as a prototype to design a carbon fiber reinforced plastic (CFRP) engine hood, analyzes the dynamic performance of the engine hood and optimizes the dynamic stiffness index while considering lightweight of the structure. Taking the layer thickness of each ply orientation of the CFRP engine hood as the design variable, the optimal Latin hypercube design (Opt-LHD) method is applied for uniform sampling. Moreover, the Kriging model method and response surface model (RSM) method are used to construct the surrogate model of the total mass, equivalent dynamic stiffness of critical points, and the first-order modal frequency. Then the Non-dominated Sorting Genetic Algorithm NSGA-II is used for multi-objective optimization with the equivalent dynamic stiffness and mass of the CFRP engine hood as the optimization objective. Finally, the optimized CFRP engine hood was trial-produced and compared with the original steel engine hood. The results indicate that the optimized CFRP engine hood has better dynamic stiffness performance; furthermore, the lightweight effect reaches 24.4 %.
1. Introduction
Automotive lightweight is mainly achieved through new lightweight materials, structural optimization design, and advanced material manufacturing methods [1]. As a new lightweight material, carbon fiber reinforced plastic (CFRP) has many advantages, and it is widely used in automotive body structures [2]. Guo et al. [3] used the principle of equal stiffness substitution to replace the material of the steel engine hood with CFRP, and compared the mechanical properties with each other. The results indicated that the CFRP engine hood has improved its mechanical properties (e.g., stiffness), and the mass was reduced by 46 %. Birk et al. [4] designed and developed vehicle body panels using CFRP for an electric vehicle, achieving a weight reduction of more than 20 %. Duan et al. [5] carried out multi-objective optimization for crash-worthy composite materials, which greatly improved the specific energy absorption of the structure and reduced the structure’s peak load of the structure while reducing the structural mass.
This paper applies CFRP to the engine hood, and takes the thickness of the inner and outer panels of the engine hood as the design variable. In addition to mass, the dynamic stiffness of the CFRP engine hood is used as the optimization objective for multi-objective optimization. The optimal Latin hypercube design (Opt-LHD) method is used to establish the sample space, the response surface model method and the Kriging model method are used to establish the surrogate model. The genetic algorithm is used for lightweight design. The optimized CFRP hood is trial-produced, and dynamic stiffness tests and modal tests are carried out.
2. Simulation analysis of steel engine hood
Generally, the main static performance indexes of the engine hood include bending stiffness, torsional stiffness, lateral stiffness. Bending stiffness is divided into two working conditions: front point bending condition and back point bending condition. As shown in Fig. 1. For the torsional condition, the constraints are shown in Fig. 2. The lateral rigidity condition is shown in Fig. 3. At the same time, the first-order modal frequency can also be obtained through optistruct solver.
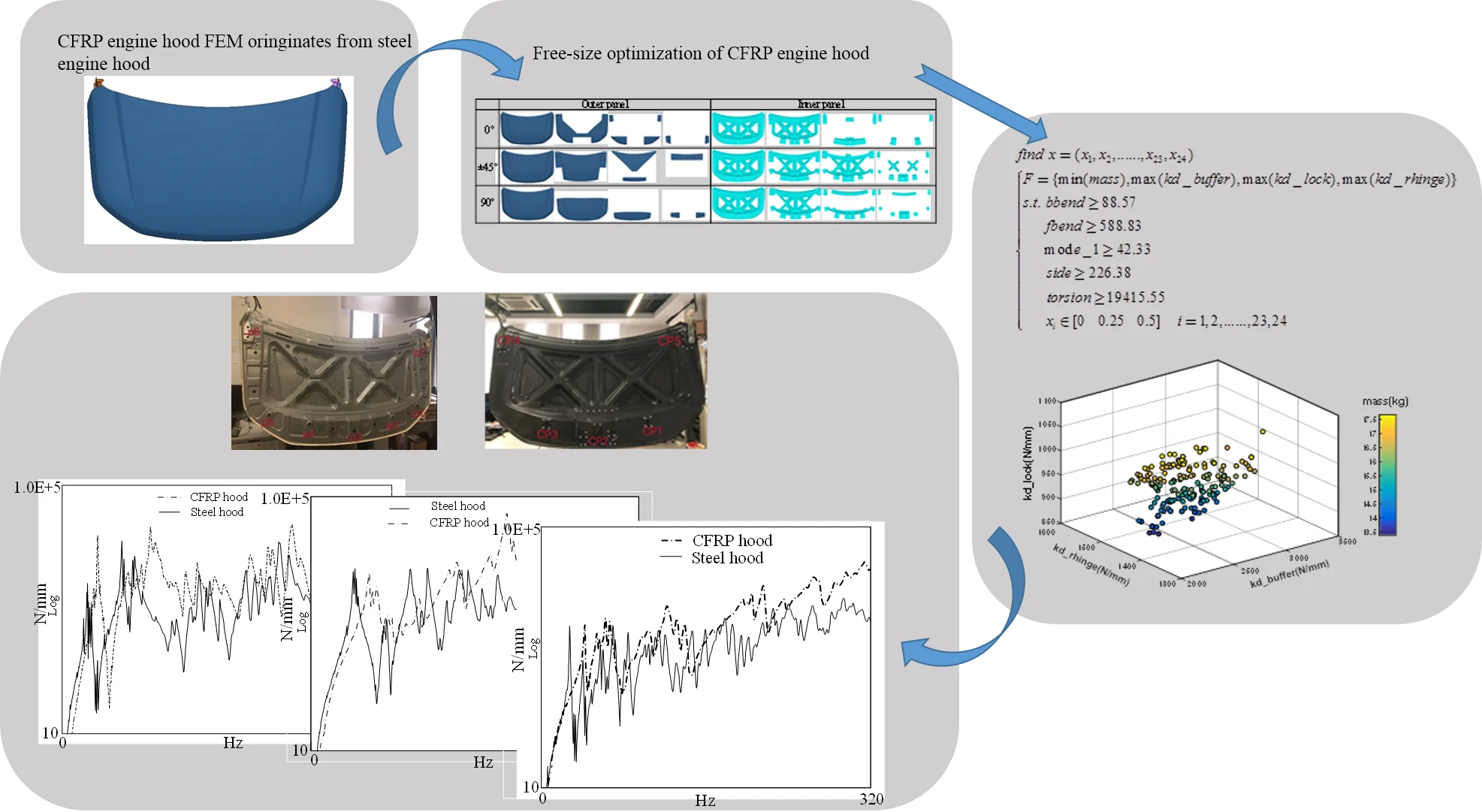
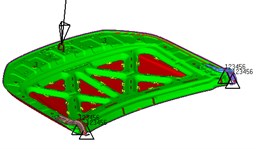
Fig. 1Bending conditions
a) Front point bending condition
b) Back point bending condition
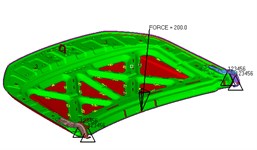
Fig. 2Torsion condition
Fig. 3Lateral loading conditions
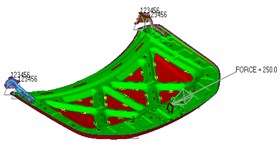
The simulation results of the original steel engine hood are shown in Table 1. The static parameters of the steel engine hood will be used as the constraint index for the subsequent multi-objective optimization.
Table 1Simulation results of steel hood
Parameter | Results |
Front point bending stiffness (N/mm) | 423.73 |
Back point bending stiffness (N/mm) | 103.68 |
Torsion stiffness (Nm/rad) | 18520.98 |
Lateral stiffness (N/mm) | 210.46 |
First-order modal frequency (Hz) | 40.5 |
3. Free-size optimization of CFRP engine hood
The inner and outer panels of the engine hood can be simplified into four hyper-laminate composite laminates. To avoid the warpage and deformation of the trial-produced hood, it is required that the thickness and quantity of the CFRP laminates at the two orientations of 45°/-45° of the inner and outer panels are equal. The commercial software solver optistruct is used for free-size optimization.
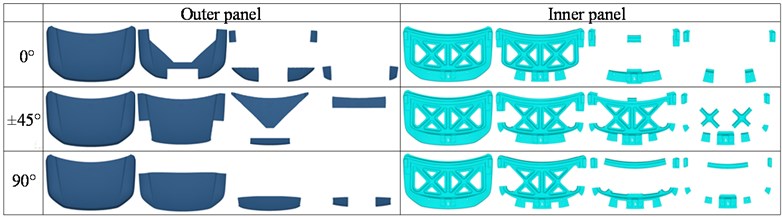
Free-size optimization can divide each hyper laminate into several sub-layer. This paper obtained four kinds of stacking forms in each orientation after free-size optimization. For manufacturing convenience, each stacking form needs to be sorted out. The results after sorting is shown in Fig. 4.
4. Multi-objective optimization of CFRP engine hood
The current commercial optimization software can only take static indexes (e.g., mass and structure compliance) as optimization objectives, but cannot take dynamic performance as optimization objectives. Therefore, this paper proposes a multi-objective optimization scheme considering dynamic indicators of the engine hood.
Fig. 4The stacking form of the outer panel and inner panel after sorted out
4.1. Selection of design variables
In the previous section, 24 kinds of stacking forms were obtained under the four-ply orientations of the inner and outer panels of the engine hood. And the thickness of these 24 stacking forms was used as design variable. The value of the thickness variable is set to a multiple of 0.25, which is the current minimum thickness of CFRP material that can be manufactured. If the ply thickness of a specific stacking form is 0, it means that this sub ply can be removed from the structure. At the same time, to reduce the interlayer stress, it is required that the number of adjacent layers with the same ply orientation should not be higher than two. Thus, the level of each thickness factor is [0, 0.25, 5].
4.2. Selection of optimization goals and constraints
The lightweight body can directly increase the specific power of the vehicle, effectively reduce fuel consumption and reduce emissions, which are of considerable significance to energy conservation and environmental protection. At the same time, lightweight can directly reduce the materials used to manufacture vehicles and reduce costs. Therefore, the weight of the hood is considered as an essential optimization objective.
For the engine hood, the higher the equivalent dynamic stiffness value, the better its dynamic performance. This paper selects the equivalent dynamic stiffness of several critical points of the engine hood as the optimization objectives, as shown in Fig. 5.
Fig. 5Critical points of the engine hood
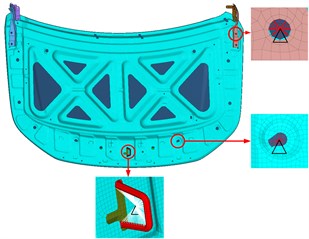
Fig. 6Pareto optimal solution set
The vehicle is subjected to various dynamic excitations during driving, usually, the primary excitation of the road is in the low-frequency stage of 0-20 Hz. The first-order modal frequency of the engine hood is generally required to be higher than 40 Hz. Thus, the first-order modal frequency of the CFRP engine hood is used as an optimization constraint, and the first-order modal frequency is required to be greater than that of the original steel hood.
4.3. Surrogate model
In this paper, the Opt-LHD is used to establish 325 sample points for the design variables of 24 factors with 3 levels. These 325 sample points are submitted to optistruct solver for calculation to prepare for the establishment of subsequent surrogate models.
The response surface model (RSM) is selected to establish the surrogate model of the static index of the CFRP engine hood, which includes bending stiffness, torsion stiffness, lateral stiffness and mass.
Kriging model is used to establish surrogate model for the equivalent dynamic stiffness of kd_buffer, kd_lock and kd_rhinge, and so on the first-odder modal frequency mode_1. Meanwhile, the matern Cubic function is used for fitting the deviation of these surrogates.
After obtaining the surrogate model, it is necessary to validate the accuracy of the model. The commonly used model error analysis index is . The larger the value of , the higher the accuracy of the surrogate model. The of the surrogate model of each response point is as shown in Table 2. It can be seen from the table that the of each surrogate model is more than 0.9, which indicates that the fitting effect is ideal.
Table 2The R2 of surrogate models
Surrogate model | Surrogate model | ||
Torsion stiffness | 0.957 | kd_lock | 0.976 |
Lateral stiffness | 0.968 | kd_rhinge | 0.985 |
Front point bending stiffness | 0.964 | mass | 1 |
Back point bending stiffness | 0.914 | First-order modal frequency | 0.942 |
kd_buffer | 0.987 |
4.4. Multi-objective optimization
Considering the static and dynamic performance of CFRP engine hood, the thickness of each layer of CFRP hood is taken as the design variable, and its static stiffness performance is taken as the constraint to carry out multi-objective optimization. The mathematical model is as follows:
where bbend refers to the back point bending stiffness, fbend refers to the front point bending stiffness, torsion refers to the lateral stiffness and the mode_1 refers to the first-order modal frequency of the CFRP engine hood.
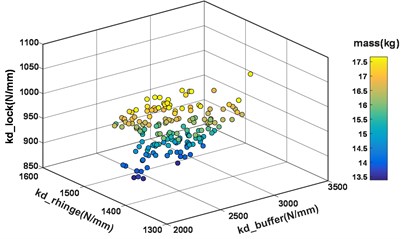
The genetic algorithm (NSGA-II) is used to perform 500 iterations of optimization, and 189 sets of Pareto optimal solutions were obtained. The bubble chart of Pareto solution set is shown in Fig. 6. As shown in the figure, when the mass of the CFRP engine hood is at a relatively high level, the equivalent dynamic stiffness values of kd_buffer, kd_lock and kd_rhinge are all at a relatively high level. However, Excessive mass does not meet the original intention of the lightweight design. Considering the lightweight design, an optimal solution is selected in Pareto solution sets as the optimization scheme, which is the darkest bubble point in Fig. 6.
After getting the optimal thickness of each layer of CFRP engine hood, the stacking sequence of each ply orientation is optimized with optistruct solver to obtain better performance. Table 3 shows the thickness of each layer and the stacking sequence of each layer of the optimal solution.
Table 3The result of multi-objective optimization
Variables | Thickness(mm) | Variables | Thickness(mm) | ||
Outer panel | PLYS11100 | 0.25 | Inner panel | PLYS25100 | 0 |
PLYS11200 | 0 | PLYS25200 | 0 | ||
PLYS11300 | 0 | PLYS25300 | 0.5 | ||
PLYS11400 | 0.25 | PLYS25400 | 0.25 | ||
PLYS12100 | 0 | PLYS26100 | 0 | ||
PLYS12200 | 0.25 | PLYS26200 | 0 | ||
PLYS12300 | 0.25 | PLYS26300 | 0 | ||
PLYS12400 | 0 | PLYS26400 | 0.5 | ||
PLYS14100 | 0.25 | PLYS28100 | 0.25 | ||
PLYS14200 | 0 | PLYS28200 | 0 | ||
PLYS14300 | 0.25 | PLYS28300 | 0 | ||
PLYS14400 | 0.5 | PLYS28400 | 0.5 | ||
Mass (kg) | 13.69 | ||||
kd_lock (N/mm) | 1359.6 | ||||
kd_buffer (N/mm) | 2042.1 | ||||
kd_rhinge (N/mm) | 891.3 | ||||
Comparing the optimal results obtained by the surrogate model with the finite element simulation results, as shown in Table 4, the relative error of the optimization objective is within the acceptable range, which indicates that the surrogate model meets the precision requirements and can replace the actual finite element model to predict the simulation results.
Table 4The error analysis of surrogate models
Optimization objectives | Predicted value | Simulation value | Relative error (%) |
Mass (kg) | 13.38 | 13.54 | 1.18 |
kd_buffer (N/mm) | 2042.1 | 1960.7 | 4.150 |
kd_lock (N/mm) | 1259.6 | 1226.7 | 2.682 |
kd_rhinge (N/mm) | 891.3 | 942.4 | 5.422 |
5. Verification of test results
The optimized CFRP engine hood is trial-produced, and the dynamic stiffness test and modal test are carried out to compare with the original steel engine hood. As shown in Fig. 7.
Fig. 7Critical points of two engine hood

a) Key points in steel engine hood

b) Key points in CFRP engine hood
For the steel engine hood, point P1, P2, P4, P5 are the installation positions of the buffer block, which are usually subjected to impact loads. Point P3 is the lock installation position. Point P6 and P7 are the hinge points connected to the vehicle body. For the CFRP engine hood, point CP1, CP3 are the installation positions of the buffer block. Point CP3 is the lock installation position. Point CP6 and CP7 are the hinge points connected to the vehicle body. The hammering method is selected for excitation for this test. We can obtain the dynamic stiffness curves by installing the three-way acceleration sensor at the key points of the engine hood and exciting at these points in direction with a hammer. Since the engine hood is a symmetrical structure, just selecting one buffer installation point and one hinge point to analyze. The results are shown in Fig. 8. The dynamic stiffness of the CFRP engine hood has improved in the entire analysis frequency range compared with the steel engine hood, and its equivalent dynamic stiffness value is also higher compared with the steel hood, which is consistent with the simulation results.
Fig. 8Dynamic stiffness curves of two engine hoods
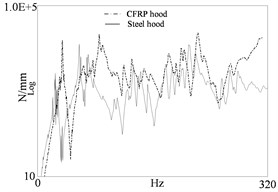
a) At the installation point of the buffer block
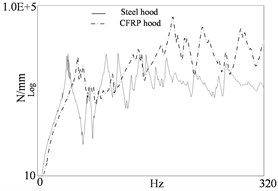
b) At the locking point
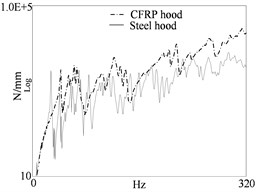
c) At the hinge point
6. Conclusions
The results show that the mass of the optimized CFRP engine hood is reduced to 13.38 kg from 17.69 kg, and the equivalent dynamic stiffness of the buffer block installation point is increased by 13.25 % compared with the steel hood. The equivalent dynamic stiffness of the locking point is increased by 10.69 % compared with the steel hood. The equivalent dynamic stiffness of the hinge point is increased by 8.12 % compared with the steel hood. Meanwhile, the test results indicate that the dynamic stiffness level of CFRP hood is higher than that of steel hood in the frequency range, which is consistent with the simulation results.
References
-
Gao Y., Liu Z., Xu Y. Application research of CFRP in automobile panels. Automotive Engineering, Vol. 7, Issue 1, 2020, p. 978-984, (in Chinese).
-
Ma F., Xiong C. Optimization and performance analysis of CFRP automotive b-pillar reinforced plate. Journal of Hunan University (Natural Sciences), Vol. 48, Issue 8, 2019, p. 36-44, (in Chinese).
-
Guo Y., Huang X. Development of carbon fiber engine hood based on the equal stiffness principle automobile. Applied Technology, Vol. 19, Issue 1, 2020, p. 100-103, (in Chinese).
-
Birk F., Ali F., Weigold M. Lightweight hybrid CFRP design for machine tools with focus on simple manufacturing. The International Journal of Advanced Manufacturing Technology, Vol. 108, Issue 11, 2020, p. 3915-3924.
-
Duan S., Tao Y., Han X. Investigation on structure optimization of crashworthiness of fiber reinforced polymers materials. Composites part B-engineering, Vol. 60, Issue 1, 2014, p. 471-478, (in Chinese).
