Narrowbandness of seismic ground displacement on a broader area of the lithosphere and importance on base motion in isolated structures

1. Introduction

Records of ground seismic displacement have not attracted much awareness because in dynamic analysis of conventional fixed structures, or the vast majority of buildings, ground acceleration records are the important signals [1-3]. However, in dynamics of base-isolated structures, ground displacement can be a more important seismic record than the acceleration one [4-7].

Base isolation is a very successful anti-seismic technique [1, 4, 8] that has proved great performance indeed during real earthquakes [9, 10]; nevertheless, it has a problem, that one of large base displacements which is a side effect of the technique. The large base displacement problem (LBD problem) can be explained and tackled considering the relative displacement of the base [11, 12] or studying the absolute base displacement [4, 13]; when considering relative displacement the problem is normally or has been more lately called isolator displacement demand [14, 15].

The LBD problem has been solved, or it has been shown that the absolute base displacement can be reduced to well under ground displacement levels [4]. It has been suggested that the reduction in absolute base displacement implies a reduction in relative base displacement because a) the latter is simply equal to the first minus the ground displacement record ($u_b\left(t\right)-s\left(t\right)$) which is set or fixed (at least in a strong motion by strong motion basis) and b) the before-reduction absolute displacement levels are larger than the ground displacement ones $\text{(}{u}_b>s\text{)}$ [4]. Nevertheless, this idea or suggestion has not been demonstrated yet; thus, actual relative or isolator displacement mitigation will be discussed in this work as an extension of the application of the results.

Now, this solution of the LBD problem was based on an important hypothesis regarding the modeling of the seismic input. This hypothesis in turn was based on a frequency-domain characterization of actual strong motion ground displacement, which was established through the analysis of the power spectral density (PSD) of displacement records of four (4) large California earthquakes (moment magnitude above 7.0) [4]. Subsequent research or broader results were necessary in the context of Northern America, and next ten (10) California strong-motion events were analyzed [16]; these later spectral results corroborated the previous and limited-in-number ones; nevertheless, there is still the geographic limitation, or the fact that the earthquakes analyzed were confined or associated solely to the Californian section of the Pacific and North American plates boundary. Thus, results on a broader region of the lithosphere are still necessary.

In this work, broader results are presented, which are from strong motion events associated with the Nazca, South American, Cocos, Caribbean, North American and Pacific plates; that is, the spectral content of ground displacement of 8 very large Latin American earthquakes is studied (2 events with magnitude above 8); more exactly, the PSD of the critical horizontal-component record of the closest station to epicenter is analyzed. The results would let us state –on a much wider geographical base– that horizontal ground displacement is a narrow-band process. One important point and also an enhancement relative to previous research, is that seismic stations in this larger region of the world are newer or have broad-band sensors; therefore, concerns on the low and high frequency noise levels associated with seismic records are reduced, and this point is discussed in the last Section.

The narrow-band main result shall be important by itself, but apart from scientific importance, the results will also corroborate that the engineering problem of large base displacements in isolated structures can be solved [4] within simple passive control. More expensive and complex solutions to the LBD problem or the displacement demand in isolated buildings are presently being proposed: active control [6, 17], semiactive control [18], hybrid control with mangnetorheological dampers [19], tuned mass dampers [12, 20] and the inerter or gyromass [21]. In addition, it is pointed out that the study of seismic ground displacement is important also in engineering of submerged tunnels, pipelines and long-span structures [22, 23]. Finally, it is also noted that the suggested solution of the LBD problem is based on a linear model of the isolation system; nonetheless, there are nonlinear models [24] which require advanced numerical methods for the structural response [25].

2. Method and analysis of seismic base isolation application

The procedure to obtain the main results of this investigation are presented first, which are broader ground displacement power spectral density results; secondly, the extension of their application to mitigating the relative base displacement in isolated structures is explained; this motion is actually the isolator deformation or displacement, which is important in the engineering and construction of real isolation systems.

2.2. Extension of the applications to reduce isolator displacement

As previously indicated, one application of the initial PSD results was in the reduction of the absolute base displacement in isolated structures; in fact, the mitigation was successful or to well under ground displacement levels [4]. Nonetheless, the physical design and construction of an isolation system is more concerned with the relative displacement than with the absolute one; this is mainly because the width of the moat and the flexibility of service connections depend on that isolator displacement (displacement demand) which is established by the dynamic design of the system or by seismic codes.

This relative displacement problem is a current issue in Earthquake Engineering; in fact and as explained previously, more complex and expensive solutions to this LBD problem have recently been proposed [17-21]; thus, the spectral content of seismic ground displacement should be revisited; moreover, the narrow-band results must be confirmed in larger regions of the world, and as importantly, the aim or application must be on the control of relative base displacement this time around.

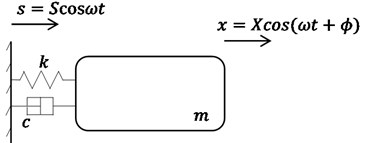
With this last objective in mind, for further work and for expanding the application of the PSD results, we propose as solution to the isolator (relative) displacement problem to make use of the frequency-domain concept of relative transmissibility from the field vibration isolation of mechanical engineering. The hypothesis is that if the absolute transmissibility function made possible quite good reductions in absolute base motions [4], good levels of isolator displacement mitigation can be as well attained if the relative transmissibility is considered. This function is not new; however, the concept is not at all as widespread as its absolute counterpart: whereas this can be found in all undergraduate textbooks on Mechanical Vibrations, the relative transmissibility does not appear in most textbooks on the subject; this is because isolator clearance is not a big concern in mechanical engineering, and also because absolute transmissibility is associated not only with displacement isolation but also with force isolation whereas the relative transmissibility applies only for displacement attenuation [26]. As a matter of fact, if we consider the most popular textbooks (English language or worldwide) on mechanical vibrations, the book by Thomson [27] is the only one that has the notion although indirectly rather than as a direct presentation as found in a more advanced or professional references as the Harris’ Shock and Vibration Handbook [26]. In these very few references in which the concept appears, it is established that if the system of Fig. 1 is excited by a stationary harmonic displacement of the support, $s$, the relative displacement of the structure, $x$, is also harmonic with the same frequency $\omega$, as shown in the figure where $X$ and $S$ are the amplitudes of mass and ground motions, respectively; more importantly, the relative transmissibility is the ratio of these harmonic amplitudes, and is further defined by [26, 27]:

1

$T_r=\frac{X}{S}=\frac{r^2}{\sqrt{{\left(1-r^2\right)}^2+{\left(2\zeta r\right)}^2}},$

where $r$ is the frequency ratio and $\zeta$ damping factor.

As it is proposed herein, the optimization of $T_r$ can or must be the basis of a design procedure of base-isolation systems when the relative LBD problem is a concern, or its control is an objective, in the full design process of isolated structures. Now, the idea is based on the seismic input being narrow band, which is validated in this paper, and the methodology will be similar to the one published previously to solve the absolute LBD problem [4]. All this is currently the subject of further research work, and we emphasize that the proposal or idea of making use of relative transmissibility is original. Two additional comments or annotations, the proposal will be valid under both, near-field and far-field conditions, and the displacement demand problem in the isolation technique is not exclusive of civil buildings; structures as electric substation transformers and nuclear power plants do have the same issue under seismic load [28, 29], which can further expand the applications of the spectral results presented.

Fig. 1Standard one-degree-of-freedom system under harmonic motion of support

3. Ground displacements power spectral density results

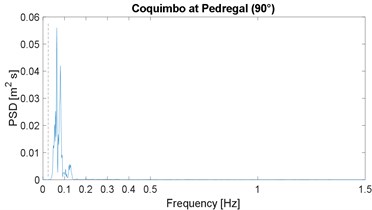
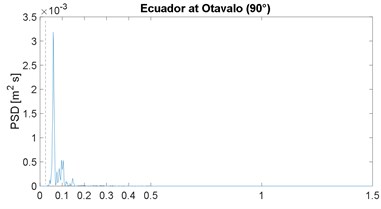
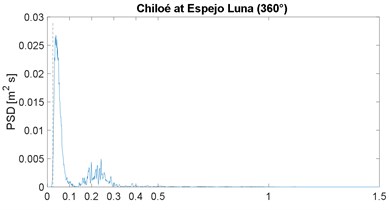
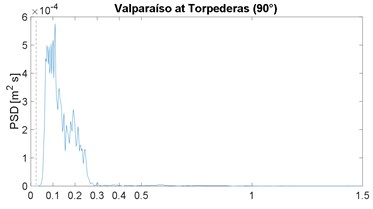
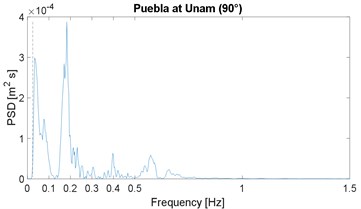
The PSD function of the selected strong-motion displacement signals is shown in Fig. 2; it includes the corresponding horizontal component or angular information. These results confirm the narrow-band characteristic previously noticed in the works by Morales [4, 16]; note that the plot range 0-1.5 Hz is already a very slender spectral range. As in the previous works, the narrow band is similar in all cases, except for the Maule event which is justified later; in other words, the energy below 0.025 Hz is close to zero, the peak value is between 0.05 and 0.18 Hz, and above 0.40 Hz the spectral content is negligible; the 0.025 Hz frequency is marked by the vertical dashed line, in all PSDF figures. In addition, the mean value of the peak-power frequency is 0.10 Hz, which is below but close to the 0.13 of the previous two works [4, 16].

A discussion is in order regarding the problem of low frequency, or long period, noise levels associated with strong motion records [30] because this can be severe for frequencies below 0.1 Hz. However, in this regard this work also presents an enhancement relative to previous spectral results: most seismic stations in Latin America are newer or these have broad-band sensors; therefore, the low-frequency noise problem is very limited. This can be proven, the low-cut frequency in the processing of all records is between 0.02 and 0.06 Hz (mean value equal to 0.03 Hz) which is below the frequencies in which we are observing rich spectral content; in other words, it was assumed in the processing or by the analysts, that the signal-to-noise ratio was, in general, problematic for frequencies below 0.03 Hz, or periods above 30 s. As an example, most important records of the 1995 Northridge event (California) had a low processed frequency of 0.1 Hz.

The Maule at Constitución PSD is distinct because liquefaction was widespread on the rupture zone; in particular, several types of liquefaction occurred in the small city of Constitución [31]. It is important to note that the same type of spectral content was noticed in a site of the previous work that also suffered liquefaction; that is, peaks in the PSD functions around 0.3 Hz rather than around 0.1 Hz, which is the case in a normal or most of the records analyzed [16].

Fig. 2Power spectral density of ground displacement

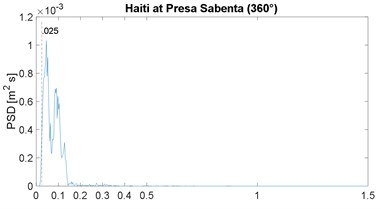
a)

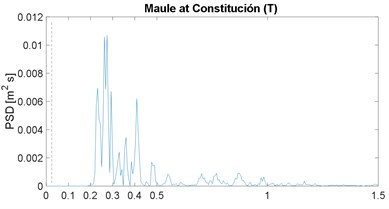
b)

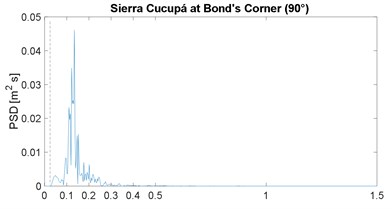
c)

d)

e)

f)

g)

h)

4. Conclusions

Strong-motion records on a much broader area of the lithosphere have been analyzed. It can be concluded or it is confirmed that horizontal ground displacement is practically a narrow-band process; this is based on the analysis of 8 very large earthquakes (2 events with magnitude above 8) in the vast Latin American region. These results corroborate previous ones, and that the absolute LBD problem in isolated structures can be solved by vibrations analysis in the frequency domain.

Moreover, a proposal has been presented to extend the application of the further and broader results to control the isolator displacement or deformation, which from an engineering or construction point of view, is more important than the control of the absolute base displacement; this is because the relative displacement is the one having direct impact on the seismic gap or the unusable and costly space between structure and moat walls, and on the expense of flexible utility connections and size of the isolators. This is a present-day problem for which more expensive techniques than simple base isolation are being implemented, as active and hybrid control, and also complex inertial additions as tuned mass dampers and inerters.

The lowest frequency of the band for this set can be established as 0.025 Hz; it had previously been set as 0.049 Hz for strong-motion records in a limited region or the State of California, USA; this difference or presence of lower dominant frequencies in some events is the result of geological diversity, which in a whole continent is richer than in a single state of a country.