Bending of a circular flexible plate taking into account the initial curvature

Mamatova, G. U.; Sugirbekova, А. K.; Bekaulov, N. M.

doi:10.21595/vp.2020.21751

Vibroengineering Procedia

Browse Procedia

Published: 26 November 2020

Check for updates

Bending of a circular flexible plate taking into account the initial curvature

G. U. Mamatova¹

А. K. Sugirbekova²

N. M. Bekaulov³

¹Department of Chemical Physics and Materials Science, Al-Farabi Kazakh National University, Almaty 050040, Kazakhstan

²Department of Chair of Mathematics, Physics and Informatics Teaching Methods, Abai Kazakh National Pedagogical University, Almaty 050010, Kazakhstan

³Department of Computer Engineering and Information Security, International IT University, Almaty 050000, Kazakhstan

Corresponding Author:

G. U. Mamatova

Cite the article Download PDF

Abstract

In this article, an analytical solution of the problem of bending a round plate with an initial curvature is obtained. A round plate with an initial curvature as a structural element is widely used, the calculation of which leads to many questions related to the design of round Foundation plates, turbine disks, flexible shaft connections and other. The nonlinear theory of round flexible plates provides the key to explaining the process of loss of stability, which often leads to complete destruction of the structure. Therefore, there is a high need for analytical methods for solving problems of calculating the stress-strain state of round flexible plates, taking into account the initial curvature. These problems are mathematically reduced to differential equations with variable coefficients, the exact solution of which, as a rule, does not exist. Therefore, the construction of analytical solutions to these problems is very relevant.

Bending of a circular flexible plate taking into account the initial curvature

1. Introduction

The problem of bending elastic round plates of initial curvature is one of the actual problems of the technical theory of elasticity. A round plate with an initial curvature as a structural element is widely used, which is calculated by many questions related to the design of round Foundation plates, turbine disks, flexible shaft connections, hydraulic machine blades, disk springs, etc. [1], The development of modern practice requires researchers and designers to create methods for solving a large number of strength problems related to the variability of thickness, elastic modulus, Poisson's ratio, and the presence of initial curvature in aggregates. There is a high need for analytical and approximate analytical methods for solving problems of calculating the stress-strain state of inhomogeneous plates, taking into account the initial curvature. Existing studies of symmetrical bending of round plates with initial curvature are of a particular nature. Asymmetric bending of round plates of variable thickness has been studied even less; here, in addition to solutions for hyperbolic profile plates, there are practically no solutions for any other profiles of practical significance. These problems are mathematically reduced to differential equations with variable coefficients, the exact solution of which, as a rule, does not exist. Therefore, the construction of analytical solutions to these problems is very relevant [2]. This work substantially fulfills the specified gap. Using the method of partial discretization of differential equations, based on the theory of generalized functions, an analytical solution to the problem of bending elastic round plates with account for the initial curvature is obtained.

2. Materials and methods

Let’s consider a round plate that is fixed along the contour in a certain way. We will assume that the plate is ring-shaped with external and internal radii $r_{b}$ , $r_{a}$ and thickness $h$ .

Fig. 1Basic designations when considering a round plate

In this case, the deflections are symmetrical with respect to the axis $z$ and the deflection, as well as all other values that characterize the stressed and deformed state, will be functions only $r$ . When constructing solutions to the solving equations, we use the partial discretization method, which allows us to construct an analytical solution to the problem of bending a round flexible plate with an initial deflection, fixed along the contour and subjected to a uniformly distributed transverse load of intensity $q$ . In this case, the deflection, as well as all other values that characterize the stressed and deformed state, will be functions of only $r$ .

The basic system of differential equations of the theory of a flexible round plate with initial deflection has the following form [3]:

1

\{\begin{array}{l} D \frac{d}{d r} (\nabla^{2} ω) = ψ + \frac{h}{r} \frac{d Φ}{d r} (\frac{d ω}{d r} + \frac{d ω_{i n}}{d r}), \\ \frac{d}{d r} (\nabla^{2} Φ) = - \frac{Е}{r} (\frac{1}{2} {(\frac{d ω}{d r})}^{2} + \frac{d ω_{i n}}{d r} \frac{d ω}{d r}), \end{array}

where $ψ$ is the load function equal to $ψ = \frac{1}{r} \int_{0}^{r} q r d r$ , $Φ$ is the voltage function entered by the formulas:

σ_{r} = \frac{1}{r} \frac{d Φ}{d r}, σ_{φ} = \frac{d^{2} Φ}{d r^{2}},

and $E$ is the elastic modulus, $ω$ is the deflection, $σ_{r}$ , $σ_{φ}$ are radial and tangential stresses.

Using the method of partial discretization of differential equation [3], we write the second equation of the system Eq. (1) as:

2

\frac{d^{3} Φ}{d r^{3}} + \frac{1}{r} \frac{d^{2} Φ}{d r^{2}} - \frac{1}{r^{2}} \frac{d Φ}{d r} = - \frac{1}{2} \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) (\frac{E}{r_{k}} (\frac{1}{2} {(\frac{d ω_{k}}{d r})}^{2} + \frac{d ω_{i n_{k}}}{d r} \frac{d ω_{k}}{d r}) δ (r - r_{k})

- \frac{E}{r_{k + 1}} (\frac{1}{2} {(\frac{d ω_{k + 1}}{d r})}^{2} + \frac{d ω_{i n_{k + 1}}}{d r} \frac{d ω_{k + 1}}{d r}) δ (r - r_{k + 1})) .

The general solution of Eq. (2) will be:

\frac{d Φ}{d r} = C_{1} r + C_{2} \frac{1}{r} - \frac{1}{4} \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) (\frac{E}{r_{k}} (\frac{1}{2} {(\frac{d ω_{k}}{d r})}^{2} + \frac{d ω_{i n_{k}}}{d r} \frac{d ω_{k}}{d r}) (r - \frac{r_{k}^{2}}{r}) H (r - r_{k})

- \frac{E}{r_{k + 1}} (\frac{1}{2} {(\frac{d ω_{k + 1}}{d r})}^{2} + \frac{d ω_{i n_{k + 1}}}{d r} \frac{d ω_{k + 1}}{d r}) (r - \frac{r_{k + 1}^{2}}{r}) H (r - r_{k + 1})) .

Consider a plate with a hole that is pivotally supported along the contour, then the boundary conditions are Eq. [4]:

3

{\frac{1}{r} \frac{d Φ}{d r}|}_{r = r_{a}} = 0,

4

{M_{r}|}_{r = r_{b}} = D {(\frac{d^{2} ω}{d r^{2}} + \frac{μ}{r} \frac{d ω}{d r})}_{r = r_{b}} = 0,

5

{ω|}_{r = r_{b}} = 0 .

Due to the fact that the $r_{a}$ is not subject to a smallness constraint, we will assume an arbitrary constant $C_{2}$ equal to zero. By virtue of condition Eq. (3), the solution of problem Eq. (2, 3) will be:

6

\frac{d Φ}{d r} = - \frac{E}{4} \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) (\frac{1}{r_{k}} (\frac{1}{2} {(\frac{d ω_{k}}{d r})}^{2} + \frac{d ω_{i n_{k}}}{d r} \frac{d ω_{k}}{d r}) (r - \frac{r_{k}^{2}}{r}) H (r - r_{k})

- \frac{1}{r_{k + 1}} (\frac{1}{2} {(\frac{d ω_{k + 1}}{d r})}^{2} + \frac{d ω_{i n_{k + 1}}}{d r} \frac{d ω_{k + 1}}{d r}) (r - \frac{r_{k + 1}^{2}}{r}) H (r - r_{k + 1})) .

Substitute the resulting expression in the first equation of the system Eq. (1) and we will perform further discretization of the multiplier $d ω / d r$ in the right part of this equation. Then the first equation of the system Eq. (1) will take the form:

7

\frac{d^{3} ω}{d r^{3}} + \frac{1}{r} \frac{d^{2} ω}{d r^{2}} - \frac{1}{r^{2}} \frac{d ω}{d r} = \frac{ψ}{D} - \frac{E}{4} \frac{h}{D \cdot r} \cdot \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) (\frac{1}{r_{k}} (\frac{1}{2} {(\frac{d ω_{k}}{d r})}^{2} + \frac{d ω_{i n_{k}}}{d r} \frac{d ω_{k}}{d r})

\times (r - \frac{r_{k}^{2}}{r}) H (r - r_{k})

- (\frac{1}{r_{k + 1}} (\frac{1}{2} {(\frac{d ω_{k + 1}}{d r})}^{2} + \frac{d ω_{i n_{k + 1}}}{d r} \frac{d ω_{k + 1}}{d r}) (r - \frac{r_{k + 1}^{2}}{r}) H (r - r_{k + 1})) \frac{d ω_{i n}}{d r}

- \frac{E}{8} \frac{h}{D \cdot r} \frac{d ω}{d r} \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) (\frac{1}{r_{k}} (\frac{1}{2} {(\frac{d ω_{k}}{d r})}^{2} + \frac{d ω_{i n_{k}}}{d r} \frac{d ω_{k}}{d r}) (r - \frac{r_{k}^{2}}{r}) H (r - r_{k})

- \frac{1}{r_{k + 1}} (\frac{1}{2} {(\frac{d ω_{k + 1}}{d r})}^{2} + \frac{d ω_{i n_{k + 1}}}{d r} \frac{d ω_{k + 1}}{d r}) (r - \frac{r_{k + 1}^{2}}{r}) H (r - r_{k + 1})) \cdot \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) (δ (r - r_{k}) - δ (r - r_{k + 1})) .

After the corresponding transformations, taking into account the properties of generalized functions and conditions Eq. (4), we get:

8

\frac{d ω}{d r} = \frac{r}{2 D} \int ψ d r - \frac{1}{2 D r} \int r^{2} ψ d r - \frac{r}{2 D} [\int_{r = r_{b}} ψ d r + \frac{1 - μ}{1 + μ} \cdot \frac{1}{r_{b}^{2}} \int_{r = r_{b}} r^{2} ψ d r]

+ \frac{E h r}{8 D} \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) [(\frac{1}{2} {(\frac{d ω_{k}}{d r})}^{2} + \frac{d ω_{i n_{k}}}{d r} \frac{d ω_{k}}{d r}) (\frac{1}{r^{2}} \int (\frac{r^{2}}{r_{k}} - r_{k}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r

- \int (\frac{1}{r_{k}} - \frac{r_{k}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r - \frac{μ - 1}{r_{b}^{2} (1 + μ)} \int_{r = r_{b}} (\frac{r^{2}}{r_{k}} - r_{k}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r

+ \int_{r = r_{b}} (\frac{1}{r_{k}} - \frac{r_{k}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r) - (\frac{1}{2} {(\frac{d ω_{k + 1}}{d r})}^{2} + \frac{d ω_{i n_{k + 1}}}{d r} \frac{d ω_{k + 1}}{d r})

\times (\frac{1}{r^{2}} \int (\frac{r^{2}}{r_{k + 1}} - r_{k + 1}) \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r - \int (\frac{1}{r_{k + 1}} - \frac{r_{k + 1}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r

- \frac{μ - 1}{r_{b}^{2} (1 + μ)} \int_{r = r_{b}} (\frac{r^{2}}{r_{k + 1}} - r_{k + 1}) \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r + \int_{r = r_{b}} (\frac{1}{r_{k + 1}} - \frac{r_{k + 1}}{r^{2}}) \frac{d ω_{i n}}{d r}

\times H (r - r_{k + 1})] + \frac{E h r}{16 D (1 + μ)} \sum_{k = 2}^{n} (r_{k + 1} - r_{k - 1}) (1 + \frac{r_{k}^{2}}{r_{b}^{2}} + μ (1 - \frac{r_{k}^{2}}{r_{b}^{2}})

- (1 + μ) (1 - \frac{r_{k}^{2}}{r_{}^{2}}) H (r - r_{k})) (\sum_{i = 1}^{k - 1} (r_{i} + r_{i + 1}) ((\frac{1}{2} {(\frac{d ω_{i}}{d r})}^{2} + \frac{d ω_{i n_{i}}}{d r} \frac{d ω_{i}}{d r}) (\frac{1}{r_{i}} - \frac{r_{i}^{}}{r_{k}^{2}})

- (\frac{1}{2} {(\frac{d ω_{i + 1}}{d r})}^{2} + \frac{d ω_{i n_{i + 1}}}{d r} \frac{d ω_{i + 1}}{d r}) (\frac{1}{r_{i + 1}} - \frac{r_{i + 1}^{}}{r_{k}^{2}}))) \frac{d ω_{k}}{d r} - \frac{E h r}{16 D (1 + μ)} (r_{n} - r_{n + 1})

\times (1 + \frac{r_{n + 1}^{2}}{r_{b}^{2}} + μ (1 - \frac{r_{n + 1}^{2}}{r_{b}^{2}}) - (1 + μ) (1 - \frac{r_{n + 1}^{2}}{r_{}^{2}}) H (r - r_{n + 1}))

∙ (\sum_{i = 1}^{n} (r_{i} + r_{i + 1}) ((\frac{1}{2} {(\frac{d ω_{i}}{d r})}^{2} + + \frac{d ω_{i n_{i}}}{d r} \frac{d ω_{i}}{d r}) (\frac{1}{r_{i}} - \frac{r_{i}^{}}{r_{n + 1}^{2}})

- (\frac{1}{2} {(\frac{d ω_{i + 1}}{d r})}^{2} + \frac{d ω_{i n_{i + 1}}}{d r} \frac{d ω_{i + 1}}{d r}) (\frac{1}{r_{i + 1}} - \frac{r_{i + 1}^{}}{r_{n + 1}^{2}}))) \frac{d ω_{n + 1}}{d r} .

In this case $q = c o n s t$ , the analytical expression of the rotation angle at points $r_{k}$ for has the expression:

9

\frac{d ω_{1}}{d r} = \frac{q r_{1}^{3}}{16 D} - \frac{q c^{2} (3 + μ) r_{1}}{16 D (1 + μ)},

10

\frac{d ω_{2}}{d r} = \frac{\frac{q r_{2}}{16 D} (r_{2}^{2} - \frac{c^{2} (3 + μ)}{(1 + μ)})}{1 - \frac{E h r_{2} (r_{3} - r_{1})}{32 D (1 + μ)} [1 + \frac{r_{2}^{2}}{c^{2}} + μ (1 - \frac{r_{2}^{2}}{c^{2}})] \{(r_{1} + r_{2}) {(\frac{d ω_{1}}{d r})}^{2} \frac{1}{r_{1}} (1 - \frac{r_{1}^{2}}{r_{2}^{2}})\}},

for $j = \bar{3, n}$ .

11

\frac{d ω_{j}}{d r} = ⟨\frac{q r_{j}}{16 D} (r_{j}^{2} - \frac{c^{2} (3 + μ)}{1 + μ}) + \frac{E h r_{j}}{32 D (1 + μ)} \{\sum_{k = 2}^{j - 1} (r_{k + 1} - r_{k - 1}) [1 + \frac{r_{k}^{2}}{c^{2}} + μ (1 - \frac{r_{k}^{2}}{c^{2}})

- (1 + μ) (1 - \frac{r_{k}^{2}}{r_{j}^{2}})] \sum_{i = 1}^{k - 1} (r_{i} + r_{i + 1}) [{(\frac{d ω_{i}}{d r})}^{2} (\frac{1}{r_{i}} - \frac{r_{i}}{r_{k}^{2}}) - {(\frac{d ω_{i + 1}}{d r})}^{2} (\frac{1}{r_{i + 1}} - \frac{r_{i + 1}^{}}{r_{k}^{2}})] \frac{d ω_{k}}{d r}\}⟩

/ [1 - \frac{E h r_{j}}{32 D (1 + μ)} (r_{j + 1} - r_{j - 1}) [1 + \frac{r_{j}^{2}}{c^{2}} + μ (1 - \frac{r_{j}^{2}}{c^{2}})]

\times \sum_{i = 1}^{j - 1} (r_{i} + r_{i + 1}) [{(\frac{d ω_{i}}{d r})}^{2} (\frac{1}{r_{i}} - \frac{r_{i}^{}}{r_{j}^{2}}) - {(\frac{d ω_{i + 1}}{d r})}^{2} (\frac{1}{r_{i + 1}} - \frac{r_{i + 1}^{}}{r_{j}^{2}})]] .

Integrating Eq. (8) and taking into account condition Eq. (5), we write the solution of the first differential equation of the system Eq. (1) as:

12

ω = \frac{q}{64 D} (r^{4} - r_{b}^{4}) + \frac{q r_{b}^{2} (3 + μ)}{32 D (1 + μ)} (r_{b}^{2} - r_{}^{2}) + \frac{E h}{8 D} \sum_{k = 1}^{n} (r_{k} + r_{k + 1}) [(\frac{1}{2} {(\frac{d ω_{k}}{d r})}^{2}

+ \frac{d ω_{i n_{k}}}{d r} \frac{d ω_{k}}{d r}) (\int (\frac{1}{r} \int (\frac{r^{2}}{r_{k}} - r_{k}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r

- r \int (\frac{1}{r_{k}} - \frac{r_{k}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r) d r

- \int_{r = r_{b}} (\frac{1}{r} \int (\frac{r^{2}}{r_{k}} - r_{k}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r - r \int (\frac{1}{r_{k}} - \frac{r_{k}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r) d r

+ \frac{1 - μ}{2 (1 + μ)} (\frac{r^{2}}{r_{b}^{2}} - 1) \int_{r = r_{b}} (\frac{r^{2}}{r_{k}} - r_{k}) \frac{d ω_{i n}}{d r} H (r - r_{k}) d r + (\frac{r^{2}}{2} - \frac{r_{b}^{2}}{2}) \int_{r = r_{b}} (\frac{1}{r_{k}} - \frac{r_{k}}{r^{2}})

\times \frac{d ω_{i n}}{d r} H (r - r_{k}) d r) - (\frac{1}{2} {(\frac{d ω_{k + 1}}{d r})}^{2} + \frac{d ω_{i n_{k + 1}}}{d r} \frac{d ω_{k + 1}}{d r}) (\int (\frac{1}{r} \int (\frac{r^{2}}{r_{k + 1}} - r_{k + 1})

\times \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r - r \int (\frac{1}{r_{k + 1}} - \frac{r_{k + 1}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r) d r

- \int_{r = r_{b}} (\frac{1}{r} \int (\frac{r^{2}}{r_{k + 1}} - r_{k + 1}) \times \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r

- r \int (\frac{1}{r_{k + 1}} - \frac{r_{k + 1}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r) d r + \frac{1 - μ}{2 (1 + μ)} (\frac{r^{2}}{r_{b}^{2}} - 1)

\times \int_{r = r_{b}} (\frac{r^{2}}{r_{k + 1}} - r_{k + 1}) \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r

+ (\frac{r^{2}}{2} - \frac{r_{b}^{2}}{2}) \int_{r = r_{b}} (\frac{1}{r_{k + 1}} - \frac{r_{k + 1}}{r^{2}}) \frac{d ω_{i n}}{d r} H (r - r_{k + 1}) d r)]

+ \frac{E h}{16 D} \sum_{k = 2}^{n} \{(r_{k + 1} - r_{k - 1}) [(1 + \frac{1 - μ}{1 + μ} \cdot \frac{r_{k}^{2}}{c^{2}}) \frac{r^{2}}{2} - \frac{r_{k}^{2}}{1 + μ} - 1 + \frac{r_{k}^{2}}{c^{2}} - (\frac{r^{2}}{2} - 1) (1 - \frac{r_{k}^{2}}{r^{2}}) H (r - r_{k})] + \{\sum_{i = 1}^{k - 1} (r_{i} + r_{i + 1}) [(\frac{1}{2} V_{i}^{2} + V_{i n_{i}} V_{i}) (\frac{1}{r_{i}} - \frac{r_{i}}{r_{k}^{2}})

- (\frac{1}{2} V_{i + 1}^{2} + V_{i n_{i + 1}} V_{i + 1}) (\frac{1}{r_{i + 1}} - \frac{r_{i + 1}}{r_{k}^{2}})]\} V_{k}\} .

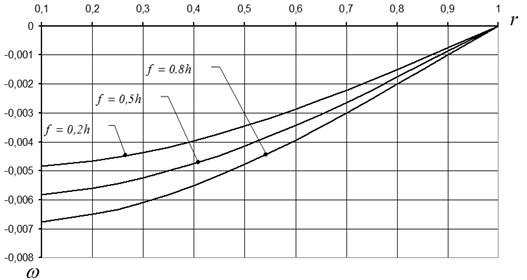
Fig. 2 shows graphs of deflection changes for a flexible round plate with different initial deflections.

3. Results and discussion

To obtain a solution of the system of resolving differential equations of the problem under consideration, A. S. Volmir sets the deflection form and then uses the method of Bubnov-Galerkin. A system of equations is often solved by a small parameter method, when the multiplier before the nonlinear terms is small. If there is no such restriction on this multiplier, then getting a solution is problematic. Therefore, we can use the method of partial discretization of differential equations, the accuracy of the resulting solution for which has been repeatedly checked when solving problems related to obtaining plate bends.

The Fig. 2 shows the bending curve of the flexible plate for $ω_{i n} = f_{i n} {(1 - r^{2} / r_{b}^{2})}^{2}$ individual initial values of the deflection boom $f_{i n} .$

Fig. 2Deflection change curves for: fin=0,2h; fin=0,5h; fin=0,8h; h= 0,02 m; q= 104 N/m2; E= 2⋅1011 N/m2; μ= 0,3.

4. Conclusions

The existing method of finding solutions to the nonlinear differential equations of Bubnov-Galerkin [5], although it is very useful, but in the General formulation of the problem and the tendency of the number of linear combinations of a given linear independent system to infinity, cannot guarantee even a weak convergence of the approximate solution to the exact one. In this regard, the application of the partial discretization method to the system of nonlinear equations under consideration is very appropriate.

References

Reddy J. N. Theory and Analysis of Elastic Plates and Shells. CRC Press, Taylor and Francis, 2007.

Publisher
Szilard R. Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods. John Wiley & Sons, 2004.

Publisher
Volmir A. S. Flexible Plates and Shells. Moscow, State Technical Publishing House, 1956.

Search CrossRef
Tyurekhodgaev, A. N., Mamatova G. U., Kalzhanova G. K. Bending of Inhomogeneous and Nonlinear Plates and Shells. LAP LAMBERT Academic Publishing is a trademark of: OmniScriptum GmbH & Co, Germany, 2015.

Search CrossRef
Smolina I. Y., Puteeva L. E., Shilnikov S. M. Calculation of Plate Bending by the Method of Bubnov-Galerkin. Tomsk: Publishing House of Tomsk State University of Architecture and Building Engineering, 2009.

Search CrossRef

About this article

Received

02 October 2020

Accepted

26 October 2020

Published

26 November 2020

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2020.21751

Keywords

the bending of the plate

stress-strain state

nonlinear differential equations

partial discretization method

class of generalized functions

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 06 30

Numerical modeling of the stress-strain state of the ice beam by specified constitutive model

Qi Xie

Research article

2018 12 31

Vibration characteristic analysis of a circular thin plate with complex pre-stress distribution

Leixin Li, Luyun Chen, Hong Yi

Research article

2018 06 30

Mathematical solutions for the flexural analysis of Mindlin’s first order shear deformable circular plates

Charles Chinwuba Ike

Research article

2018 03 31

Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates

Charles Chinwuba Ike, Benjamin Okwudili Mama

G. U. Mamatova,  K. Sugirbekova, and N. M. Bekaulov, “Bending of a circular flexible plate taking into account the initial curvature,” Vibroengineering PROCEDIA, Vol. 35, pp. 64–69, Nov. 2020, https://doi.org/10.21595/vp.2020.21751

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21751
UR  - https://doi.org/10.21595/vp.2020.21751
TI  - Bending of a circular flexible plate taking into account the initial curvature
T2  - Vibroengineering PROCEDIA
AU  - Mamatova, G. U.
AU  - Sugirbekova, А. K.
AU  - Bekaulov, N. M.
PY  - 2020
DA  - 2020/11/26
PB  - JVE International Ltd.
SP  - 64-69
VL  - 35
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Mamatova_2020,
	doi = {10.21595/vp.2020.21751},
	url = {https://doi.org/10.21595/vp.2020.21751},
	year = 2020,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {35},
	pages = {64--69},
	author = {G. U. Mamatova and {\cyrchar\CYRA}. K. Sugirbekova and N. M. Bekaulov},
	title = {Bending of a circular flexible plate taking into account the initial curvature},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]G. U. Mamatova, А. K. Sugirbekova, and N. M. Bekaulov, “Bending of a circular flexible plate taking into account the initial curvature,” Vibroengineering PROCEDIA, vol. 35, pp. 64–69, Nov. 2020, doi: 10.21595/vp.2020.21751.

Copy IEEE

Copied to clipboard!

Mamatova, G. U., А. K. Sugirbekova, and N. M. Bekaulov. “Bending of a Circular Flexible Plate Taking into Account the Initial Curvature.” Vibroengineering PROCEDIA 35 (November 26, 2020): 64–69. https://doi.org/10.21595/vp.2020.21751.

Copy Chicago

Copied to clipboard!

Bending of a circular flexible plate taking into account the initial curvature

Abstract

1. Introduction

2. Materials and methods

3. Results and discussion

4. Conclusions

References

About this article

Related Articles