An improved method for EMD modal aliasing effect

1. Introduction

With the increasing demand for mechanical on-line monitoring and intelligent diagnosis, higher requirements have been put forward for the self-adaptability, computing efficiency and fault pattern recognition efficiency of signal processing technology [1]. Empirical Modal Decomposition (EMD) is a novel signal adaptive decomposition technology, which can adaptively decompose signals into several Intrinsic Mode functions (IMF) according to its own scale, and is very suitable for processing nonlinear and non-stationary signals. EMD is an adaptive decomposition process that is performed according to the time characteristic scale characteristics of the signal itself. The result of the implementation is to separate the different frequency components in the signal layer by layer according to the frequency from high to low into corresponding IMF [2]. The IMF can be intuitive understanding as composed of a set of similar frequency narrowband signal, a correct the IMF should contain only the same scale characteristics of the signal component (note: scale characteristics is not a specific value, but a scale), as the size of different characteristics of the signal components in the same the IMF, creates a modal aliasing phenomenon. Different from the phenomenon of endpoint effect, modal aliasing may occur at any time of the signal between any adjacent IMF and have a great impact on the subsequent components [3]. If it cannot be effectively eliminated, the decomposition results will lose their physical significance. Therefore, modal aliasing is another obstacle to the application of EMD [4].

Huang firstly proposed a method of interrupt detection by setting extremum spacing parameters to control the screening of extremum points in each order of IMF screening. Although this method solves such problems very well, in practical application, this time interval is difficult to be determined before the standard EMD decomposition is implemented, which damages the self-adaptability of EMD [5]. Huang's group combined with Rilling’s group on the decomposition properties of noise. A set of white noise method (Ensemble Empirical Modal Decomposition, EEMD) is proposed to suppress aliasing and maintain the adaptive characteristics of EMD. However, this method requires multiple EMD operations, which results in low efficiency and limits its online application. Through a large number of studies on decomposing conditions, Riiling provided a theoretical basis for solving the problem of modal aliasing caused by signal interaction in the future. The validity of two signals decomposed by EMD is discussed and the condition of effective separation of two signals is given [6]. Derring proposed the influential mask signal method for the first time, which realized the separation of two similar frequency components by adding a set of mask signals. Although the amplitude of the added signal depends on experience, it provides a new idea for solving modal aliasing [7].

The most significant characteristic of EMD is the self-adaptability of decomposition, which is also the main reason that EMD has been widely studied and applied. How to improve the operational efficiency of eliminating modal aliasing on the basis of the self-adaptive decomposition of EMD has become an important topic in the application research.

2. EMD mode aliasing problem

2.1. Aliasing caused by local oscillation (interrupt signal) in a signal

For non-stationary signals, time-scale parameters are characteristic parameters based on signal characteristics. Although they have no quantitative relationship with Fourier spectrum, they can also reflect signal characteristics. According to the selected reference points, there are generally two definitions of time scale:

(a) The time span of two adjacent zero crossings; (b) the time span of two adjacent extreme points.

The above two definitions of time scales can reflect the local characteristics of signals changing with time, among which the description method based on adjacent extreme points is more effective, because even if the signal does not cross zero, the modal information of the signal can also be grasped through the span of extreme points.

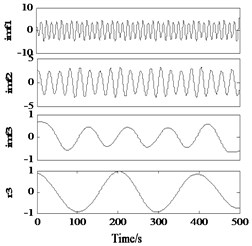
When such as Eq. (1) (as shown in Fig. 1) signal of z(t), the regularity of the harmonic signal in the local high frequency oscillation, the dramatic change in the local extreme value point spacing, according to the extreme value point fitting envelope local greatly distorted (Fig. 2), and eventually in the decomposition results, the phenomenon of the same IMF features include multiple scale (Fig. 3):

1

$z\left(t\right)=\left\{\begin{array}{lll}\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{b}\mathrm{a}\mathrm{n}\mathrm{d}& \mathrm{c}\mathrm{o}\mathrm{s}(2\pi t/200)& t=2000,\\ & +& \\ \mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}& 0.2\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi t/12\right)& t\in \left[\mathrm{1180,1200}\right].\end{array}\right.$

Fig. 1Original signal containing local oscillation

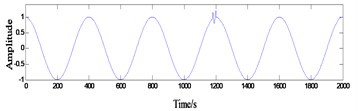
Fig. 2Local distortion occurs in the upper and lower envelope

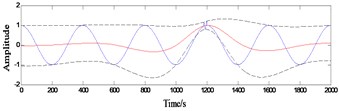
2.2. Aliasing caused by signal amplitude-frequency relationship

Take a randomly generated 1000 points discrete Gaussian white noise as an example to perform EMD decomposition, and the results are shown in Fig. 4.

As can be seen from the Fig. 4, the noise signal is decomposed into 9 components according to the frequency from high to low, and the extreme value points of each component are $P_i$, $i=$1,…,·9. Although each IMF is a narrowband signal containing a frequency band, the distribution of the number of extreme points can reflect the frequency component characteristics of each IMF. Set ${\lambda }_i=P_i/P_{i+1}$, ${\lambda }_i$ is always around 2, i.e., on a signal cycles the IMF contains about twice the next IMF. Huang inferred from this that EMD has similar binary filtering properties.

Fig. 3Same modal component of the decomposition result contains multiple time scale components

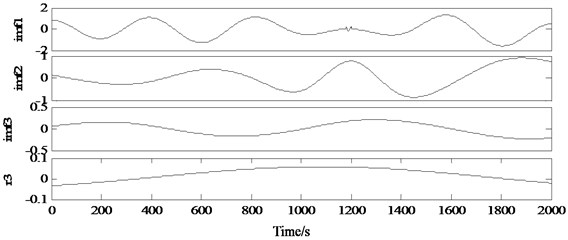
Fig. 4Gaussian white noise EMD results

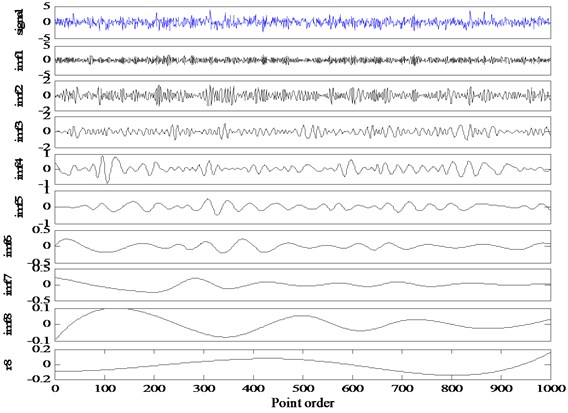
Table 1Binary decomposition characteristics of EMD

	1	2	3	4	5	6	7	8	9
Extremum points $p_i$	714	350	178	92	44	22	12	6	4
${\lambda }_i$	2.040	2.040	1.934	2.090	2	1.833	2	1.500

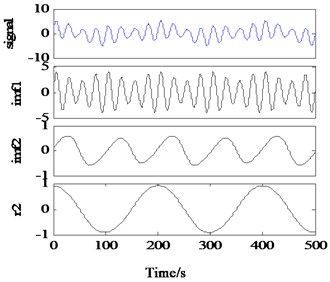
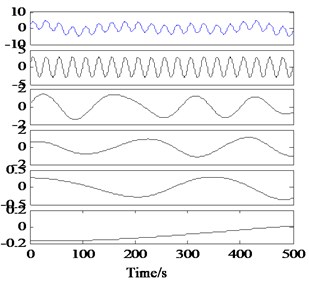
Two simulation signals $z_1\left(t\right)$ and $z_2\left(t\right)$, which are composed of four single-component signals of different frequencies, are constructed to illustrate. Where, the ratio between the frequencies of each component of signal $z_1\left(t\right)$ is 1.25, 4, and 2 respectively; The ratio between the frequencies of each component of signal $z_1\left(t\right)$ is 4, 1.3333 and 1.5, respectively. The result of EMD is shown in Fig. 5(a, b):

2

$\left\{\begin{array}{l}{z}_1\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(0.1\pi t\right)+3\mathrm{s}\mathrm{i}\mathrm{n}\left(0.08\pi t\right)+0.5\mathrm{s}\mathrm{i}\mathrm{n}\left(0.02\pi t\right)+\mathrm{c}\mathrm{o}\mathrm{s}\left(0.01\pi t\right),\\ z_2\left(t\right)=3\mathrm{s}\mathrm{i}\mathrm{n}\left(0.08\pi t\right)+0.5\mathrm{s}\mathrm{i}\mathrm{n}\left(0.02\pi t\right)+\mathrm{s}\mathrm{i}\mathrm{n}\left(0.015\pi t\right)+\mathrm{c}\mathrm{o}\mathrm{s}\left(0.01\pi t\right),\end{array}\right.$
$t=500s,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{f}_s=4.$

As can be seen from Fig. 5, it can be seen from the waveform of $z_1\left(t\right)$ and $z_2\left(t\right)$ that there is no interrupt in either signal. $z_1\left(t\right)$ is decomposed into three results, in which $r_2$ and IMF2 can basically reflect the information of two components in the original signal, while IMF1 has obvious aliasing phenomenon, because $f_1/f_2=\mathrm{}$1.25 < 2. As a result, EMD cannot separate these two modes, which verifies the Eq. (5). In fact, IMF1 is the superposition of the first two high-frequency components in $z_1\left(t\right)$, which is regarded by IMF as an IMF with certain modulation degree without separation. $z_2\left(t\right)$ is decomposed into 5 components, among which IMF1 can perfectly reflect the first component of the signal, while the subsequent components have obvious aliasing, because $f_2/f_3=\mathrm{}$1.33 < 2 and $f_3/f_4=\mathrm{}$1.5 < 2, which do not meet the frequency conditions of signal separation.

Fig. 5Modal aliasing due to close frequencies

a)$z_1\left(t\right)$

b)$z_2\left(t\right)$

3. Processing method of local impact mode aliasing

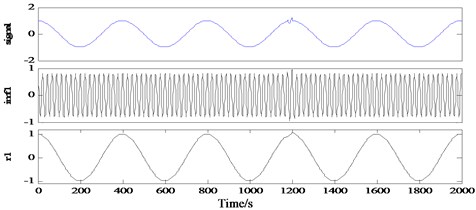
According to the characteristic that most of the local impact signals are high-frequency signals, a high frequency simple harmonic signal close to the highest frequency in the signal is added to the signal to provide the scale characteristics suitable for high frequency impact. The local high frequency and high frequency simple harmonic signals are decomposed into IMF1 to reduce the impact on the subsequent components. This algorithm does not need to perform standard EMD decomposition for the signal in advance, and has a good processing effect for the modal aliasing phenomenon caused by high frequency impact, and has a small amount of computation. In this paper, the high frequency signal frequency is set near the highest analysis frequency corresponding to the sampling frequency.

The results of EMD processing by $z\left(t\right)$ in this method are shown in Fig. 6. It can be found that although there is a small amount of residue in the impact site, the decomposition accuracy of this method is significantly. Moreover, there is no extra false component except the superposed high-frequency component.

Fig. 6EMD results of high-frequency harmonic processing with local shock signal

4. Processing method of modal aliasing at similar frequencies

Take the aforementioned simulation signal $z_1\left(t\right)$ as an example:

The two components of aliasing are $x_1\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(0.1\pi t\right)$ and $x_2\left(t\right)=3\mathrm{s}\mathrm{i}\mathrm{n}\left(0.08\pi t\right)\text{.}$ According to the analysis in Section 2.2, when the frequency ratio of two equal-amplitude signals is between 0.5 and 2, the two signals will be considered as a pattern by EMD. According to this principle, the separation of $x_1\left(t\right)$ and $x_2\left(t\right)$ can be realized if a signal $s\left(t\right)$ with appropriate frequency and amplitude can be constructed to form an aliasing mode after the superposition of $x_1\left(t\right)$ and $S\left(t\right)$. In this case, $f_1=$0.05 and $f_2=$0.04, so the lower frequency $f_L=$0.05/2 = 0.025 and the upper frequency $f_L=\text{0.05×2}\text{=}\text{1.}$ Take the frequency of $\overline{f}=\text{0.18,}$ construct $s\left(t\right)=1.5\mathrm{s}\mathrm{i}\mathrm{n}\left(0.32\pi t\right)$, set:

EMD is applied to $x_{+}\left(t\right)$ and $x_{-}\left(t\right)$, and the decomposition results, IMF₊ and IMF_-, can be obtained respectively:

Fig. 7Same modal component of the decomposition result contains multiple time scale components

a) IMF₊

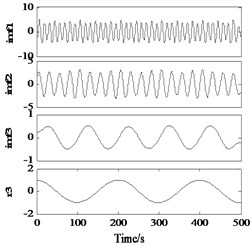
b) IMF_-

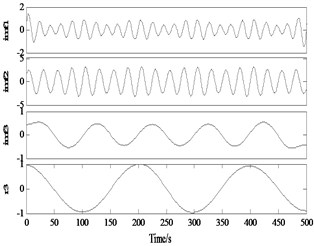
c) 0.5×(IMF₊+IMF_-)

It can be seen from Fig. 7 that in the decomposition results of $x_{+}\left(t\right)$ and $x_{-}\left(t\right)$, $x_1\left(t\right)$ and auxiliary signals are formed into alias mode, and IMF2 is successfully separated. After averaging $x_{+}\left(t\right)$ and $x_{-}\left(t\right)$, the mask component is eliminated, and the true component of $x\left(t\right)$ is obtained (deformation at the end point is caused by the endpoint effect).

Fig. 8EMD results of modal aliasing elimination method for practical hydraulic fault signals

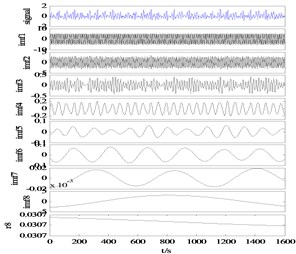
a) IMF₊

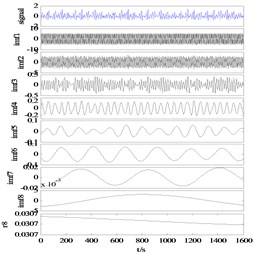
b) IMF_-

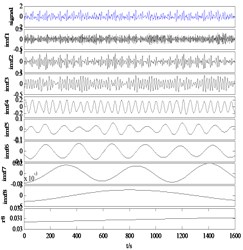
c) 0.5×(IMF₊+IMF_-)

Taking the actual hydraulic leakage signal as an example, the decomposition results are shown in Fig. 8. It can be seen from Fig. 8(a, b) that the signal is correctly decomposed to the mask signal of corresponding scale, and the decomposition result of the original signal is obtained after taking the mean value. Direct observation shows that there is no obvious aliasing in the decomposition results of this method. The reconstruction error can reach a level 10^-15.

5. Conclusions

This paper analyzes the form of EMD mode aliasing, causes, influences on EMD and solutions. The principle, characteristics, advantages and disadvantages of high frequency harmonic wave method and mask signal method are analyzed, and their respective advantages and disadvantages are verified by typical simulation signals. On the basis of the EMD adaptive characteristics, the model aliasing is quickly and effectively curbed, and the effectiveness of the method is verified by the hydraulic signal simulation, which provides a new method for the expansion of the real-time online application of EMD.