Application of sound package material in noise reduction of motor

1. Introduction

Electric vehicles are considered as the main development direction of new energy vehicles in the future because it’s more energy-saving, more environmentally friendly and more sustainable [1]. It is found that the electric vehicle motor noise is not high, but it is especially loud at high frequency [2], in the high frequency region, the traditional analysis method cannot get the specific value of each vibration response of the interior noise because of the closely spaced modes [3]. Statistical Energy Analysis (SEA) method can effectively analyze and predict the characteristics of high frequency noise in automobiles [4]. Yuksel Gur [5] et al. used SEA method to optimize the sound package of a lightweight design fuel vehicle. The SEA simulation results of vehicle and instrument panel were given and compared with the experimental data and it shows that SEA method can be used to optimize the sound package of vehicle design and is an effective sound package optimization tool based on the accurate SEA model.

The problem of large interior noise caused by motor noise of an electric vehicle is studied as follows: Firstly, establish the vehicle SEA model of the whole vehicle, and verify the accuracy of the finite element analysis model, Secondly, wrap the motor with sound package materials, at the same time, consider the influence of material thickness and the coverage ratio, the orthogonal test design method is used to obtain the optimal scheme.

2. Statistical energy analysis

The analysis method based on statistical energy is a method combining statistics and finite element analysis, it’s an important means to effectively solve the sound package analysis in medium and high frequency bands [6]. The first step of SEA method is to divide the research object into different subsystems [7], each subsystem is a conservative system, and satisfy the law of conservation of mechanical energy, then the equilibrium equation of the system can be derived [8]:

where, $\omega$ is the natural frequency, ${\eta }_{ij}$ is the coupling loss factor of subsystem $i$ to subsystem $j$, $E_i$ is the energy of subsystem $i$, ${\eta }_i$ is the internal loss factor of subsystem $i$.

Then we can get the power balance equation of the system and the energy of the system, the expression of sound pressure is as follows [9]:

where $\stackrel{-}{p}$ represents the average sound pressure of the system, $\rho$ represents the air density, $c$ represents the sound velocity, $E$ represents the system energy, $V$ represents the system volume, the subscript $i$ represents the system number.

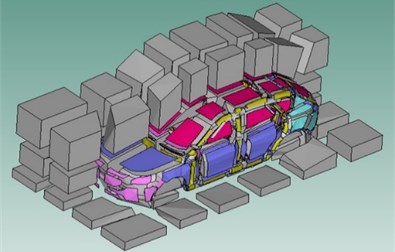
The interior sound cavity is divided into front row, rear row and trunk according to the seat position. The front row and rear row cavity are divided into head, waist and leg, and all of them are divided into left and right according to the middle of the car. The exterior sound cavity is divided into front and rear floor area, front and rear engine room area, wheel area, roof area and door area. The door area is divided into glass and door panel area, and the other cavity subsystems are divided into left and right parts. In this study, the body structure is divided into 614 panel subsystems, the interior cavity is divided into 40 subsystems, and the exterior cavity is divided into 96 subsystems. The established SEA model is shown in Fig. 1.

Fig. 1The established SEA model

3. Vehicle test and SEA model validation

3.1. Verification of PBNR

In this study, PBNR test is used to obtain the sound insulation from the driver’s head to each measuring point. PBNR can be obtained from the noise transfer function, and its calculation formula is as follows [10]:

3

$PBNR=-20{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left|p/Q_a\right|-9.5,$

where $p$ is the sound pressure, $Q_a$ is the volume acceleration of the sound source.

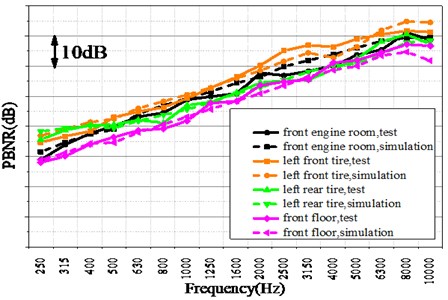
Add unit sound power excitation to the driver’s head cavity of the vehicle SEA model, the PBNR from the driver’s head to the front engine room, the front floor, the left front tire and the left rear tire are simulated, and the simulation results are compared with the test to verify the accuracy of the SEA model. Fig. 2 shows the PBNR value of the test and simulation.

Fig. 2Comparison of PBNR

3.2. Verification of exterior sound field

The verification of exterior sound field is usually needed to verify the accuracy of the SEA model. A series of measuring points are selected inside and outside the car, the measuring points inside the car should be placed at the driver’s head position. The measuring points outside the car are mainly placed in the position where the excitation is easy to transfer to the car and should cover the whole car, such as the wheel, motor, roof, floor, door, door glass and windshield glass area. The test vehicle is placed on the revolving drum test table in the semi-anechoic chamber, and the vehicle slowly accelerates to a constant speed of 100 km/h. And then the sound pressure of all measuring points is obtained. The measured sound pressure at the measured points outside the car is used as an excitation and is input into the SEA model of the electric vehicle, the sound pressure of driver’s head in the car is simulated and compared with the results directly measured in the test. Fig. 3 shows the comparison of the test and simulation results of the driver's head sound pressure level in the car.

Fig. 3Comparison of SPL

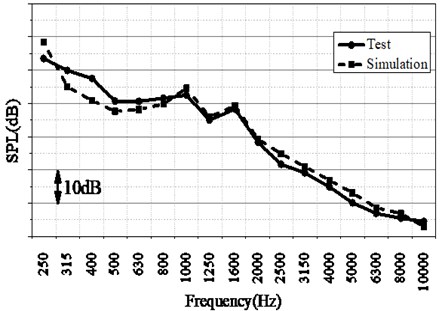
It can be seen from the Fig. 2 and Fig. 3 that in 500 to 10000 Hz, the test results of the PBNR from the driver’s head to the measuring points outside the vehicle and the SPL of the driver’s head are in good agreement with the simulation results, and the difference is less than 3 dB, which verifies the accuracy of the SEA model established in this study.

4. Optimization of motor sound package

In order to reduce the transmission of motor noise to the vehicle, the motor is packaged with double-layer sound package materials. Some studies [11-13] found that the thickness and coverage of the sound package have a great impact on the optimization of the sound package, thus it is necessary to select the package material, thickness and coverage ratio `when wrapping the motor. In this study, the orthogonal experimental design method is used to quickly obtain the optimal package scheme. There are two basic concepts in orthogonal experiment design, namely factor and level. Factor refers to the parameter that will affect the test results, and the level refers to the corresponding state of the factor. The orthogonal experimental design does not need to test all the schemes one by one, only a few representative schemes need to be selected, through the analysis of the extreme difference and the observation value, the best optimization scheme can be quickly found out from these few schemes, which greatly reduces the number of experiments and improves the efficiency [14]. After the selection, a total of four factors were selected, and they are represented by A, B, C and D respectively. Each factor has three levels which denoted by subscripts 1, 2, 3. The selection is shown in Table 1.

According to Table 1, the standard orthogonal table with four factors and three levels is selected to arrange the experiment, as shown in Table 2. The sound pressure of the motor at 100 km/s is measured at first, and input the sound pressure in SEA model in turn by the scheme listed in Table 2 for simulation. The sound pressure reduction value of the driver's head and the sound package mass are recorded. Calculate the arithmetic mean of the corresponding results for each level under each factor, and record it as ${\stackrel{-}{K}}_{ab}$, where a represents factor $a$ and $b$ represents level $b$. Calculate the extreme difference according to the formula $R_a=\max \left[{\stackrel{-}{K}}_{ab}\right]-\mathrm{m}\mathrm{i}\mathrm{n}\left[{\stackrel{-}{K}}_{ab}\right]$, the extreme difference of the factor of the inner material can be obtained [15]. The results are shown in Table 2. $R_1$ refers to the extreme difference of the reduction of driver’s head sound pressure, and $R_2$ refers to the extreme difference of sound package mass.

According to the orthogonal design theory, the bigger the extreme difference of a factor, the greater its impact on results [16]. It is customary to call the arithmetic mean of all the analysis results corresponding to a certain level of a factor as the observation value of the level of the factor, and the level corresponding to the best observation value of the average observation value of each factor is called the optimal level of the factor for the observation value. For the factor of the reduction of SPL of driver's head, the greater the reduction, the better it is, so the level corresponding to the maximum average observed value is the optimal level for this factor. For the factor of sound package mass, the smaller the better, so the level corresponding to the minimum average observation value is the optimal level for this factor, and the optimal scheme table is obtained, as shown in Table 3.

It can be seen from Table 3 that if only consider the SPL of the driver’s head, the best scheme should be $A_3{B}_2{C}_1{D}_3$, that is, the inner material is soft felt, the outer material is EVA, the thickness of inner material is 10 mm, and the coverage ratio is 80 %. If only consider the sound package mass, the best scheme is $A_2{B}_1{C}_3{D}_1$, that is, the inner material is sound-absorbing cotton, the outer material is glass fiber, the thickness of inner material is 20 mm, and the coverage ratio is 70 %. In fact, we hope that the SPL of the driver’s head will be greatly reduced, and the sound package mass will be smaller. The two schemes contradict each other and need to be considered comprehensively. For the multi-objective optimization problem with multiple factors at different levels, the optimal scheme is usually obtained by using matrix analysis method [17]. Two evaluation parameters are weighted to obtain the weight matrix affecting the test: $M={\left[\begin{array}{cc}\begin{array}{cc}\begin{array}{ccc}3.79& 5.68& 2.86\end{array}& \begin{array}{ccc}15.92& 21.63& 10.86\end{array}\end{array}& \begin{array}{cc}\begin{array}{ccc}5.03& 2.27& 4.40\end{array}& \begin{array}{ccc}2.50& 2.36& 2.30\end{array}\end{array}\end{array}\right]}^T\times {10}^{-2}$.

From the weight matrix, it can be seen that the weights of the three levels corresponding to factor A are 0.0379, 0.0568 and 0.0286, and the weight of level 2 is the largest. Similarly, the weight of level 2 of factor B, the weight of level 1 of factor C, and the weight of level 1 of factor D is the largest. Thus, the optimal scheme is $A_2{B}_2{C}_1{D}_1$, that is, the inner material is sound-absorbing cotton, and the outer material is EVA. The thickness of sound-absorbing cotton is 10 mm and the EVA is 20 mm, and the coverage ratio is 70 %. The scheme is not in the 9 schemes designed by the orthogonal experiment design method, and needs to be verified.

Fig. 4SPL of driver's head cavity

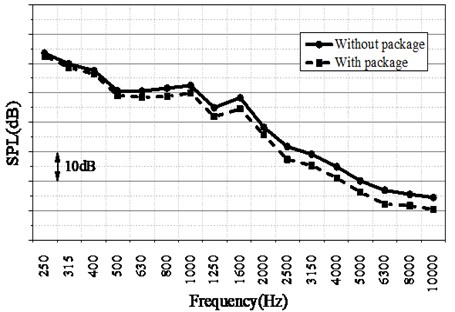
Fig. 4 shows the comparison curve of driver’s head SPL before and after the motor is wrapped according to the optimal scheme under motor excitation. It can be seen from Fig. 4 that after optimization, the SPL of the driver’s head has been reduced at various frequencies. The maximum reduction is at 6300 Hz, which is 5.70 dB, the total SPL is reduced by 2.10 dB, and the total sound package mass is 0.97 kg.

5. Conclusions

The innovation of this paper is to introduce matrix analysis method to weight multiple evaluation parameters, which provides an effective solution for multi-objective optimization of electric vehicle sound package. Based on the accurate vehicle SEA model, through the orthogonal experimental design method and the reasonable analysis of some tests, the best optimization scheme can be found to avoid the blindness of optimization, and it provides a guiding role for the optimization of the motor sound package of electric vehicles.