Optimal design of integrated main supporting structure with ultra-light weight and high stability for space camera

2.1. Traditional MSS

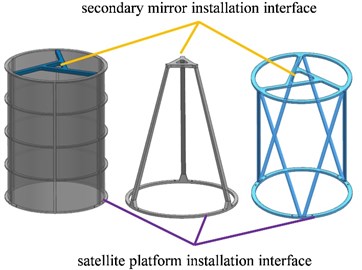
The initial 3D models of the traditional MSS are shown in Fig. 1. The satellite platform installation interface is fixed, and the mass of primary mirror and secondary mirror is connected with its own installation interface. According to the optimization method proposed in this paper, the structure is optimized. The optimization method will be described in Section 3 in detail.

Fig. 1Initial 3D models of traditional MSS

For thin-walled cylinder type, the thickness of the cylinder and ring bar, the width of longitudinal bar, and the thickness and width of the secondary mirror supporting rod are the optimized variables. After optimization, the cylinder thickness is merely 0.8 mm which is very difficult to machine and limited by the SiC/Al processing technology. The ring bar is 1mm while the longitudinal bar is 3.4 mm. The thickness and width of the secondary mirror supporting rod is 3 mm and 5 mm, respectively. The mass of thin-walled cylinder structure is 0.701 kilograms in this condition, and the FOF is 208.49 Hz. The maximum displacement of the secondary mirror (DSM) is 18 nm of the gravity field, and the temperature fluctuation is ±5 °C.

As for the rod-support type, the thickness and width of the secondary mirror supporting rod and the thickness of the MSS rod are variable. After optimization, the thickness and width of the secondary mirror supporting rod are 7.1 mm and 8 mm, respectively, the thickness of the MSS rod is 5.5 mm but its length is up to 330 mm. The mass of rod-support structure is 0.364 kilograms, and the FOF is 199.5 Hz. The maximum DSM is 15.7 nm in this rod-support type structure. This result is caused by the direct deformation of the MSS rod.

When it comes to the truss type, the thickness and length of the secondary mirror supporting rod and diameter of the MSS rod are variable. After optimization, the thickness and width of the secondary mirror supporting rod are 3.2 mm and 3.6 mm, respectively, the diameter of the MSS rod is only 5.6 mm but its length is up to 325 mm. The mass of the truss structure is 0.336 kilograms, and the FOF is 196.02 Hz. The DSM is 15.5 nm under the same condition. In this structure, there are more truss members and more connection interfaces with the upper and lower mounting boards that increases the difficulty of connection, and requires multiple embedded parts that will greatly increase the mass and makes the operability more difficult, and also accompanied with a high cost.

2.2. Performance of traditional MSS

The performance of MSS is the key source to ensure the stability of the whole camera structure. It is very important that the stiffness of MSS met the requirements. For this purpose, the engineering analysis of the optimized traditional MSSs was carried out. The properties of thin-walled cylinder type, rod-support type, and truss type are shown in Table 1.

When there were attempts to optimize three traditional MSSs, it occurred that it was difficult to ensure the FOF to meet the design requirements for three rod-support type, easier for the truss type, and for the thin-walled cylinder type. That is to say, the thin-walled cylinder type is the easiest to reach the stiffness requirement, the truss type is second, and the rod type structure is almost too difficult to realize. For the micro payload, the requirement of light weight is very strict. With the same stiffness, the thin-walled cylinder structure has the highest weight, and the rod structure is the lightest. The camera is affected by gravity load during its detection, installation, transportation, and while in orbit. The deformation of the optical elements is changed due to the excessive weight deformation which affects the imaging quality. Table 1 shows that both maximum displacement along optical axis and vertical displacement to optical axis reaches its maximum in the three rod-support type, followed by truss type, and thin-walled cylinder type and the stability of the rod type structure is poor. When the camera is in orbit, thermal environmental changes will cause thermal deformation, and this thermal deformation also affects the optical payload precision, therefore, the camera MSSs shall have high thermal stability. In the Table 1, the truss type structure has the worst thermal deformation, and the rod type structure has the best thermal stability.

Through an analysis and comparison, the thin-walled cylinder type is the best to reach the stiffness requirement, and the deformation under the gravity field is minimum. However, the mass is not suitable. The stiffness of the rod structure is lower, the deformation is the highest, its thermal stability is the best, and the mass is the lightest. The deformation of truss type structure is smaller than that of rod type structure, and its mass is lighter than that of cylinder type structure, but the thermal deformation is the largest. Structural stiffness and light weight are a pair of contradictions, and the key factor to the design of the MSS is to find its equilibrium point.

2.3. IMSS design

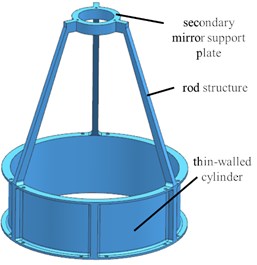
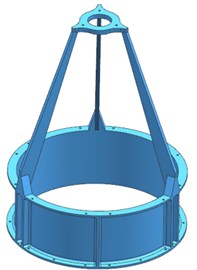
Through the study from Section 2.2, weight is reduced as much as possible to improve the structural stiffness, thus reducing the processing difficulty of the structure, a thin-walled cylinder type and rod-support type combined structure that is called IMSS is presented. The initial 3D model of IMSS is shown in Fig. 2. The IMSS is mainly composed of three parts: thin-walled cylinder, three rod structures, and the secondary mirror support plate. Hence, the IMSS is characterized by high stiffness properties of thin-walled cylinder type and high lightweight characteristics of the rod-support type structure. Three rod structures are evenly arranged with the angle of 120° so that the stress of the structure is uniformly distributed.

Fig. 2Initial 3D Models of IMSS

3.1. Structure topology

In this section, the topology optimization method is used to study the topology structure of a space camera main structure and mainly used to find the best topology form of the structure[19, 20]. Otherwise, the structure can achieve high efficiency and light weight, and improve the design efficiency. This lays the foundation for the integrated optimization.

The optimization model can be expressed as:

Optimization objective:

Constraints:

1) The IMSS shall weigh no more than 1 kilogram.

2) The DSM under gravity loads in the $X$, $Y$ and $Z$ directions shall be no more than 0.01 mm, respectively.

In this model, $C_s$ is the optimization objective that is weighted by $C_x$, $C_y$ and $C_z$. Note that $C_x$, $C_y$ and $C_z$ are the compliance functions of the whole structure under gravity in the $X$, $Y$ and $Z$ directions, respectively. $\gamma$, $\kappa$ and $\eta$ are weighting factors (this paper selects 0.33 for $\gamma$, $\kappa$ and $\eta$).

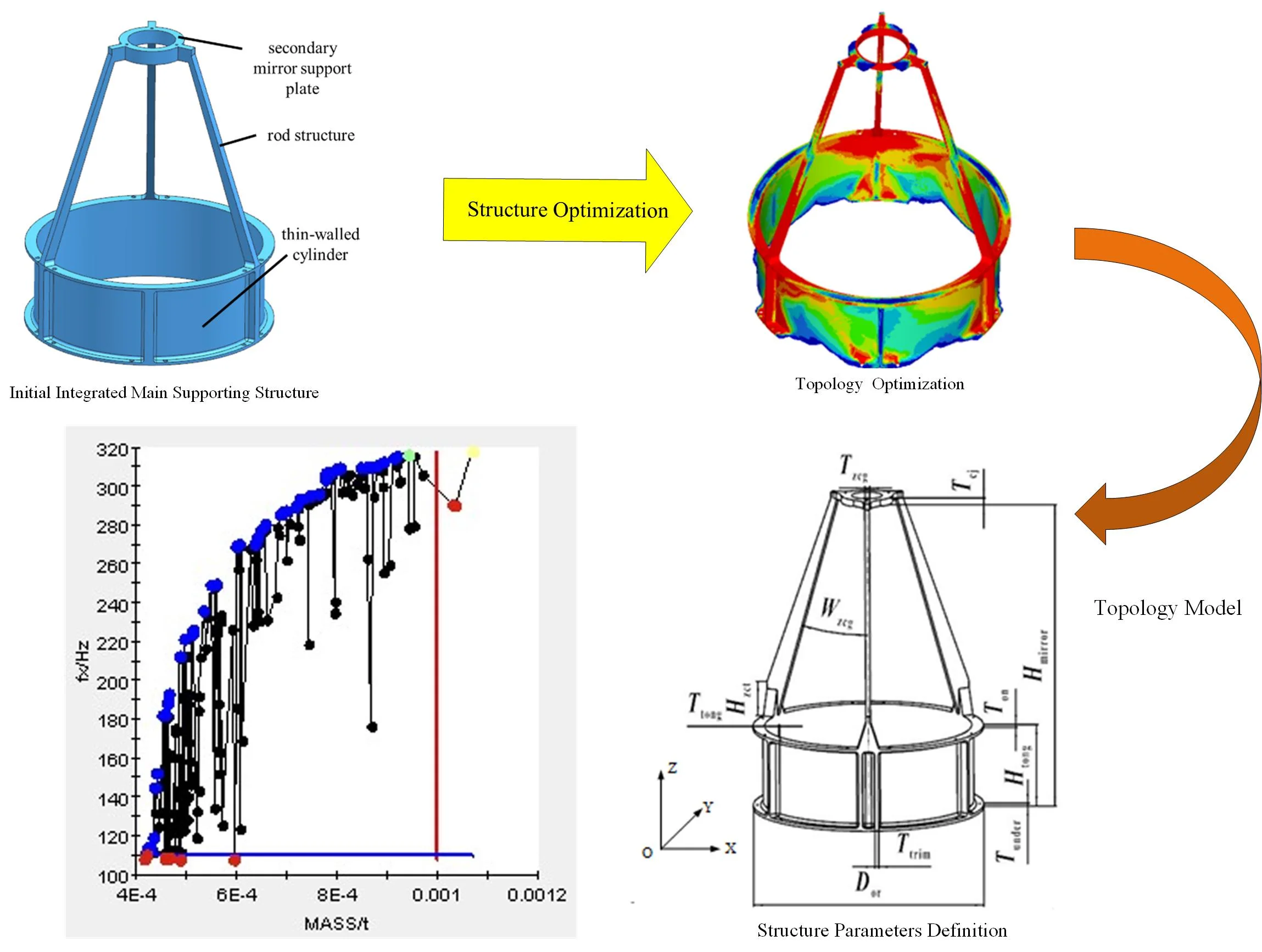
In accordance with the Initial 3D model of IMSS in Fig. 2, the FEM model of researched IMSS was established as shown in Fig. 3(a). After a large number of iterations of the optimization calculation, the authors obtained the optimal material distribution results for the optimization model under a gravity load in three directions ($X$, $Y$, $Z$). Since the topology optimization is based on the method of solid isotropic materials with penalization (SIMP), which takes the density of every FEM model element as the optimization variable, the final result given in Fig. 3(b) is shown in the form of a density cloud image. The red part indicates that the stiffness here needs to be strengthened. Based on the analysis of topology optimization results, combined with the engineering processing technology in engineering practice, the topology model of IMSS is shown in Fig. 3(c), and the mass is 0.794 kilograms.

Fig. 3Topology optimization of IMSS: a) FEM, b) topology optimization results, c) topology model

a)

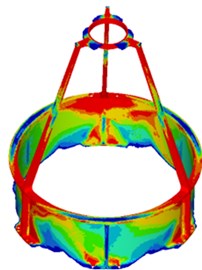
b)

c)

3.2. Traditional MSS

Traditional experiential design methods and manual debugging methods are complex in operation and have low efficiency, so it is difficult to complete the global optimal results. The integrated optimization method-based software automatically modifies the parameterized model and seeks for the optimal result through its integrated operation, and it not only improves the design efficiency, but also optimizes multiple objectives simultaneously and seeks for the global optimal solution. In this section, Unigraphics NX and MSC, Patran & Nastran are integrated through ISight to optimize the structure. UG is used for parameterized modeling, automatic updating 3D model, Patran for pre-processing, and NASTRAN for solution and analysis. The size parameter optimization design of IMSS is carried out in Isight with the mass minimum and FOF maximum as optimization objectives.

3.2.1. Parameter definition

The parameters affecting the thermal performance of IMSS are shown in Fig. 4. The distance between the primary mirror and secondary mirror $H_{mirror}$, and the outer envelope diameter of IMSS $D_{or}$ are not variable. While the others parameters, including the height and thickness of thin-walled cylinder, $H_{tong}$_, and $T_{tong}$, such thickness of the flange which connected with the platform, $T_{under}$, which thickness of the flange connected with the three rod-structures $T_{on}$, thickness of the stiffeners on thin-walled cylinder $T_{trim}$, which height of the flange connected with the rod-structure and thin-walled cylinder $H_{zct}$, the angle between rod-structure and optical axis $W_{zcg}$, thickness of the rod-structure $T_{zcg}$ and thickness of the secondary mirror support plate $T_{cj}$, are the design variables.

Fig. 4Structure parameters definition

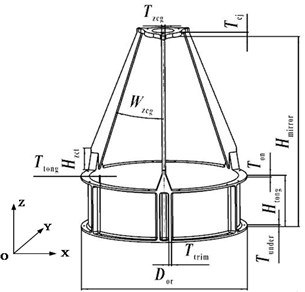
3.2.2. Optimization of proportion between truss and thin-walled cylinder

The angle between the rod-structure and optical axis $W_{zcg}$ determines the proportion of the supporting rod-structure and thin-walled cylinder. It is the key parameter to find the equilibrium point between structural stiffness and light weight. Otherwise, it is meaningful to analyze the influence of the angle on the performance for the development of the ultra-light support structure. From the structural position relationship from Fig. 4, the range of the angle $W_{zcg}$ is expressed as Eq. (2):

2

$\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{D_{or}/2}{H_{mirror}}<W_{zcg}\approx \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\frac{D_{or}}{2}}{H_{mirror}-H_{tong}}<\frac{\pi }{2}.$

Based on the solution of Eq. (2), the Eq. (3) can be gotten as follows:

3

$\frac{H_{tong}}{H_{mirror}}\approx 1-\frac{\frac{D_{or}}{2}}{H_{mirror}·\tan \left(W_{zcg}\right)}.$

Since, $H_{mirror}$, $D_{or}$ are known, the conclusion can be gotten as follows:

4

$\frac{H_{tong}}{H_{mirror}}\propto \frac{1}{\tan \left(W_{zcg}\right)}.$

Thanks to $W_{zcg}\propto \mathrm{t}\mathrm{a}\mathrm{n}\left(W_{zcg}\right)$, the following conclusion can be made:

5

$\frac{H_{tong}}{H_{mirror}}\propto \frac{1}{W_{zcg}}.$

Setting up $\alpha =\frac{H_{tong}}{H_{mirror}}$, the influence of the angle $W_{zcg}$ on the performance of IMSS can be studied by the ratio of height between the thin-walled cylinder and the distance between the primary mirror and secondary mirror ($\alpha$). Firstly, the influence of the angle on the FOF along the three orthogonal directions of the coordinate axis shall be studied. The results of the IMSS deformation in the change of primary and secondary mirror position, which directly affects the imaging quality of the camera. However, the primary mirror has little deformation and near the support plate, hence, the DSM is one of the decisive performances of the camera parameters. The influence of the angle changing the DSM under the gravity condition is also worth paying attention to. The influence of the angle on the main structure performance is shown in Fig. 5. Thanks to that the IMSS is circumferentially symmetric, the FOF in the $X$ and $Y$ directions are the same. Therefore, the curve of FOF-Y and FOF-X overlaps in Fig. 5.

Fig. 5First order frequency

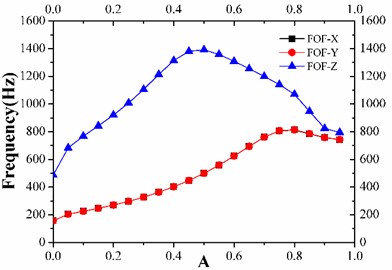
Fig. 6Mass of IMSS

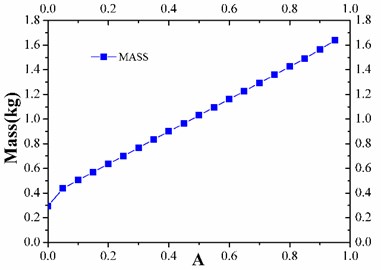
Fig. 7Displacement of secondary mirror

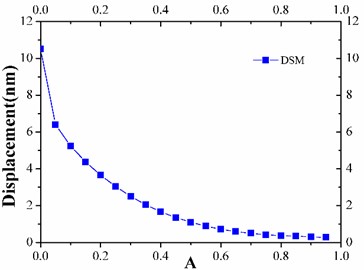
From Fig. 5, with the angle increase, the FOF along the three orthogonal directions rises first and then decreases. When the height of thin-walled cylinder, $H_{tong}$, is larger than 1/10 of the distance of primary and secondary mirror, $H_{mirror}$, the FOF is above 200 Hz, which satisfies the design requirements. From Fig. 6, the DSM is inversely proportional to the angle, and the height of the thin-walled cylinder is smaller than 1/10 of the distance between primary mirror and secondary mirror, $H_{mirror}$. The DSM exceeds 6 nm, and has serious influence on the stability of the system. According to Fig. 7, with the angle increase, the mass of IMSS increases linearly up to 1 kg beyond the design index of the main structure when the height of thin-walled cylinder is larger than 2/5 of the distance between primary and secondary mirrors. This means that the stiffness, deformation, and mass perform better when the height ratio of the rod-structure and the thin-walled cylinder is 6:1.

3.2.3. Progress of integrated optimization

The mass, deformation of secondary mirror and the FOF are the optimization objectives of main structure. The stiffness of structure is inversely proportional to DSM, ultimately, the mass and FOF are the optimization objectives, which belong to the multi-objective optimization. The mathematical description of the multi-objective optimization problem of IMSS is expressed as Eq. (6):

6

$\left\{\begin{array}{l}findX={(T_{cj},T_{zcg},T_{tong},T_{trim},T_{on},T_{on},T_{under},H_{zct})}^T,\\ \min \left(MASS\right),\max \left(f_X\right),\\ S.T.3.0\le T_{cj}\le 15.0,\\ 2.0\le T_{zcg}\le 15.0,\\ 1.5\le T_{tong}\le 6.0,\\ 1.5\le T_{trim}\le 6.0,\\ 1.5\le T_{on}\le 6.0,\\ 1.5\le T_{under}\le 6.0,\\ 0\le H_{zct}\le 50.0,\\ f_X\ge F\left(\mathrm{H}\mathrm{z}\right),\\ MASS\le M\left(\mathrm{k}\mathrm{g}\right).\end{array}\right.$

As described in Section 3.2.1, the parameterized modeling of IMSS is realized with Unigraphics NX8.0, and the finite element processing is completed with MSC Patran & Nastran. The integrated optimization process of parameterized modeling and analysis optimization is realized by Isight. The optimization process is shown in Fig. 8(a), and the solution process is shown in Fig. 6(b). The light weight and the high stiffness is a pair of contradictions. The optimization is multi-objective optimization problem. It is difficult to converge to the unique best-global optimal solution. Isight integration optimization obtains a set of feasible solutions which is called a Pareto optimal solution set. As shown in Fig. 8(b), each point in the graph is an optimization result, in which the blue dots are Pareto optimal.

Fig. 8Isight integrated optimization process

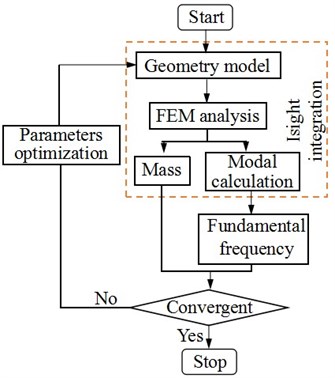
a) Optimization process

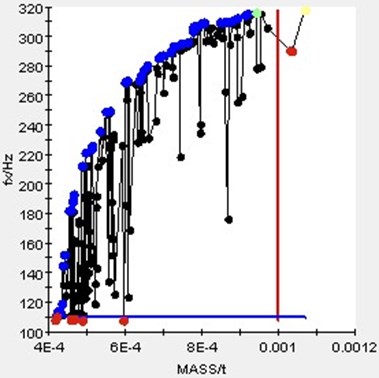
b) Solution process

The ideal solution for both the mass and the surface shape is selected from Pareto optimal solution set. The design variables, range of values, initial values, and final optimization results of the integrated optimization are shown in Table 2.

Table 2Design variables and optimization results

Variables	Range (mm)	Initial values (mm)	Optimization results (mm)
$T_{cj}$	[3.0, 15.0]	5.0	6.95
$T_{zcg}$	[2.0, 15.0]	8.0	3.01
$T_{tong}$	[1.5, 6.0]	4.0	1.72
$T_{trim}$	[1.5, 6.0]	4.0	4.02
$T_{on}$	[1.5, 6.0]	4.0	2.98
$T_{under}$	[1.5, 6.0]	4.0	3.01
$H_{zct}$	[0.0, 50.0]	5.0	30.0

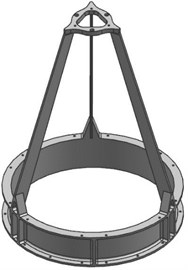
After optimization, the thickness of the thin-walled cylinder is only 1.7 mm, and the thickness of the supporting rod-structure is only 3 mm, which is far less than the thickness of the traditional value. The mass of the optimized IMSS that the final 3D model of the IMSS shown in Fig. 9 is only 0.56 kilograms that is equal to 11.2 % of the total mass of the payload, and the maximum area of the deformation appears on the support bar with the sizes of no more than 4.5 nm to meet the design requirements well.

Fig. 93D model of IMSS after integrated optimization

3.3. Performance of IMSS

The degree of light weight of the IMSS is significantly improved than that of the traditional support structure. So it is necessary to investigate whether the support structure can ensure the position accuracy and surface accuracy of the mirror to meet the design requirements of various load conditions. The results of the engineering analysis of the primary mirror are shown in Table 3 and those for the secondary mirror are shown in Table 4.

Table 4 shows that the surface precision of the primary mirror under different working conditions is less than 3.5 nm, that is far better than the optical design requirements of $\lambda$/50, $\lambda$: 632 nm wavelength. The influence of gravity on the primary mirror deformation is also very small. From Table 5, it can be seen that the surface accuracy of the secondary mirror is less than 3 nm. It comes to our attention that the temperature fluctuation makes the DSM larger in $z$-axis, but this size growth is within the design requirement range.