A novel calculation expression for the experimental friction coefficient of the ball screw

1. Introduction

As an essential part of the machinery, ball screws are widely used to convert force and motions in computer numerical controls (CNC) [1]. However, owing to the enclosed structure of the ball screw, traditional measurement methods for friction coefficient are not applicable. To accurately obtain the friction coefficient between balls and raceway, a method that is suitable for ball screws is proposed.

The existing studies mainly adopt empirical values for the friction coefficient when studying the friction performance of the ball screw. Liu studied the temperature influence of the friction torque and concluded that the value of the friction coefficient is a constant [2]. Oh K. J. proposed an accurate model for friction torque calculation, where the friction coefficient is set as a constant value of 0.003 [3]. Olaru D. carried out a new model to predict the friction torque between the balls and raceway, and the corresponding friction coefficient was set between 0.02 to 0.2 [4]. To investigate the friction performance of the ball screw more accurately, the corresponding friction coefficient should be selected as a specific value under specific working conditions. Owing to the similar structure of the ball screw, rolling bearing, and rolling linear guide, these calculation models are worthy of reference. Andersson built a friction model which is suitable for different contact and operating conditions by considering Coulomb friction, viscous friction and Stribeck friction [5]. Kraker established a mixed hydrodynamic lubrication model and calculated the Stribeck curve of the lubricated sliding bearings [6]. Cheng proposed an experimental method and established a friction coefficient equation of the rolling linear guide based on the experimental research [7]. The previous studies showed that the friction coefficient obtained from experiments is more practical than theoretical calculation.

To overcome the potential limitations for current research, this paper proposed an accurate expression for the friction coefficient based on specific experiments of the ball screw. Besides, the effects of the lubrication parameter on the friction coefficient are investigated. Moreover, the average value of film thickness is calculated and the relationship between the surface roughness and the average central film thickness is discussed.

2. Theoretical analysis and experiment research

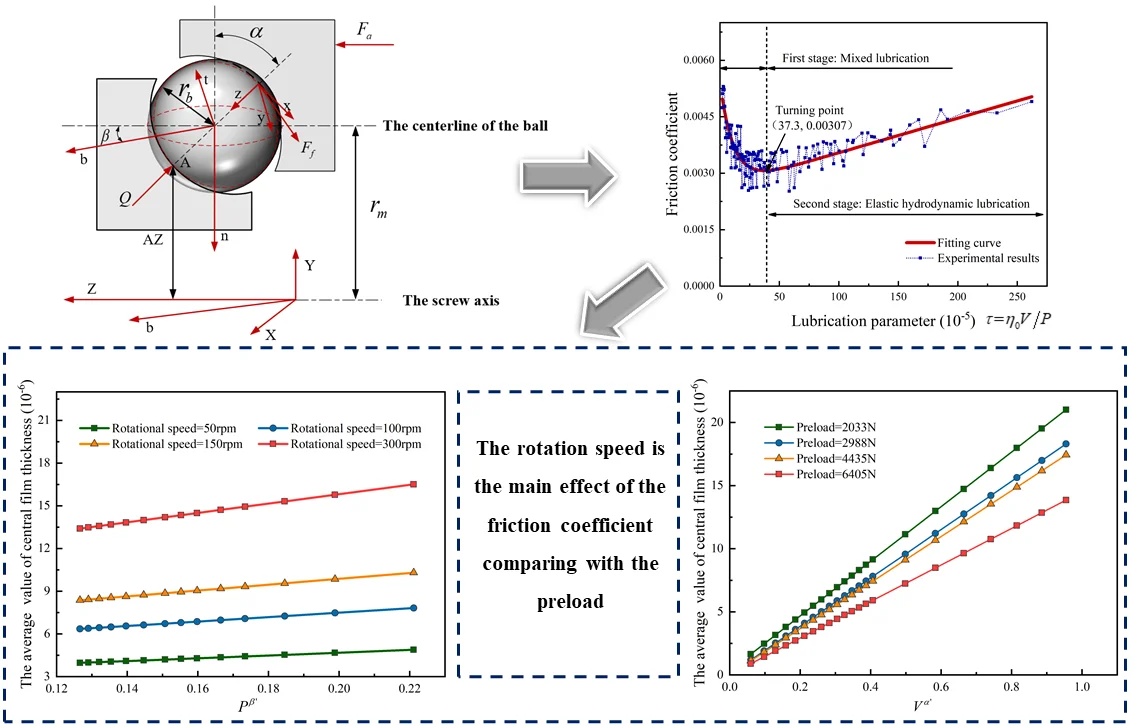
To accurately obtain the friction coefficient, the first step is to measure the friction torque which is utilized as an external characterization parameter to measure the internal friction between balls and raceway. The friction coefficient is obtained according to the correlation between the friction torque, friction coefficient and preload. Fig. 1 shows the contact model of the ball between nut and raceway and the friction torque of the preloaded ball screw $M_f$ is written as [8]:

where $F_f=f\cdot Q$ is the friction force between balls and raceway, $Q=F_p/M\cdot \mathrm{s}\mathrm{i}\mathrm{n}\alpha \cdot \mathrm{c}\mathrm{o}\mathrm{s}\beta$ is the contact force between the balls and raceway, $F_p$ is the tested value of the preload, when there is no external load applied to the ball screw, the preload is regarded as the axial load, $M$ is the actual bearing number of the ball, $f$ is the friction coefficient, $r_b$ is the radius of the ball, $r_m$ is the distance between the centerline of the ball and the screw axis, $\alpha$ is the contact angle, $\beta$ is helix angle.

Thus, the friction coefficient can be written as:

where $M_{test}$ is the tested value of the friction torque.

Fig. 1Contact model of the ball between nut and raceway

The friction torque of the ball screw is measured three times and takes the average value at each rotational speed and preload under oil lubrication (Mobil VG100). The test interval is shown in Table 1 and the corresponding friction coefficient can be calculated according to Eq. (2).

3. The expression of the friction coefficient

Referring to Jeong’s research [9], the curve fitting based on experimental results can be expressed as:

where $\tau ={\eta }_{0}V/P$ is the lubrication parameter, $V$ is the relative speed of the ball-raceway contact, $P$ is the normal force acting on the contact area, ${\eta }_0$ is the dynamic viscosity of the lubricant.

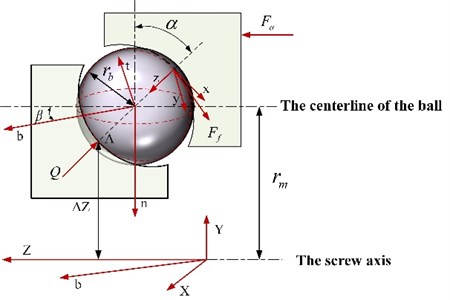
Fig. 2 shows the experimental results of the friction coefficient under the lubrication condition, and the first stage is mixed lubrication, the second stage is hydrodynamic lubrication. Due to the lower rotational speed at the beginning of the experiment, the contact force between the ball and the raceway is relatively large. As the operation progresses, the gap between balls and raceway is gradually reduced, and the boundary film gradually becomes thinner. When the boundary film is destroyed, the film thickness is lower than the height of the rough peak, and the Coulomb friction is produced by the friction between the rough peaks. Since the frictional heart generates around the rough peaks, the viscosity of the lubrication decreases. While some lubricant still exists between the higher rough peaks, the boundary lubrication state still exists when the lower rough peaks contacting with each other. In this lubrication state, the fluid and boundary film both exist. When the viscosity of the lubricant reaches the lowest point, the value of the friction coefficient is the minimum value which represents the turning point shows in Fig. 2. The second stage is hydrodynamic lubrication. At this stage, the relationship between the lubrication parameter and the friction coefficient is almost linear. Owing to the higher rotational speed, the contacting time between the ball and the raceway is extremely short, and the contact deformation is negligible.

Fig. 2The fitting curve of friction coefficient for ball screw

4. Mixed lubrication status analysis

To explain the degree of two influencing factors acting on the friction coefficient, the relation of the average central film thickness, the surface roughness, the contact load, and the relative speed is investigated based on Hamrock-Dowson’s formula [10]:

where ${V^{\alpha }}^{\text{'}}$ is velocity variable, $\alpha \text{'}=0.71\times 0.8^{\sigma /r_b}$ is the velocity index, ${P^{-}}^{\beta \text{'}}$ is the load variable, $\beta \text{'}=0.18\times 0.91^{\sigma /r_b}$ is the load index, $\sigma$ is the surface roughness of the balls and raceway, which can be detected through the surface rough meter, $h_m$ is the average central film thickness.

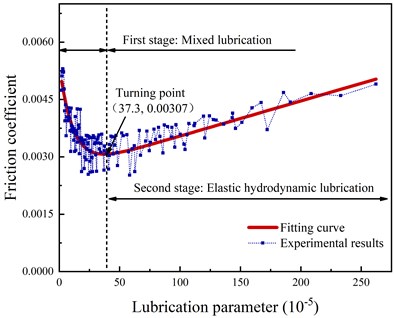
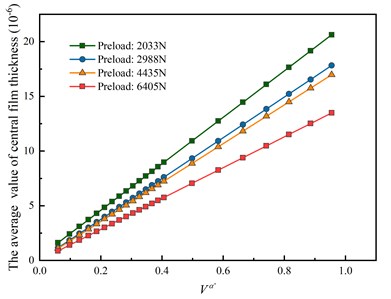
The average central film thickness under different velocity variables and load variables are shown in Fig. 3 and Fig. 4 respectively based on the approach of data fitting. Both figures show that the variations are nearly linear with the average central film thickness, which indicates a steady increasing rate under different working conditions considering surface roughness. And there is no difference in the variation curve of nut and raceway, which means the lubricant within the ball screw system is supposed to be distributed evenly through the whole running process.

In Fig. 3, the average central film thickness keeps rising along with the velocity variables, and the higher the preload is, the smaller the average central film thickness is. This is because the increasing preload provides a higher contacting load, which leads to a smaller relative speed in a unit time, leading to the decrease of the average central film thickness. In Fig. 4, with the rotational speed increases, the increasing rate of the film thickness is lower than the corresponding curves in Fig. 3, which indicates that the relative speed of the ball-raceway contact is the main factor that affects the average central film thickness. It is further illustrated that the rotation speed is the main effect of the friction coefficient comparing with the preload.

Fig. 3Effects of velocity index on the average value of central film thickness

a) Nut

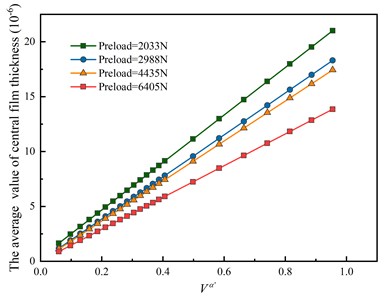
b) Raceway

Fig. 4Effects of load index on the average value of central film thickness

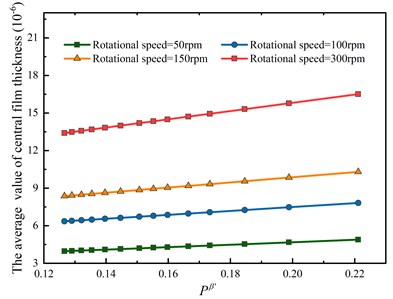
a) Nut

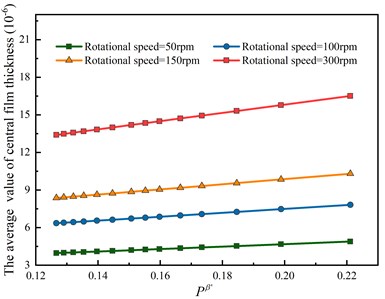
b) Raceway

5. Conclusions

This paper studied the expression of the friction coefficient based on experimental analysis of the ball screw. The friction coefficient presents a two-stage lubrication state with the increase of the lubrication parameter. The first stage is mixed lubrication and the second stage is hydrodynamic lubrication. The turning point of the two stages represents the minimum value of the friction coefficient. Besides, the rotational speed has a greater influence on the friction coefficient than the preload base on the calculation of the average oil film thickness.