Four-dimensional trajectory optimization model with priority in continuous time period

2.1. Modeling ideas

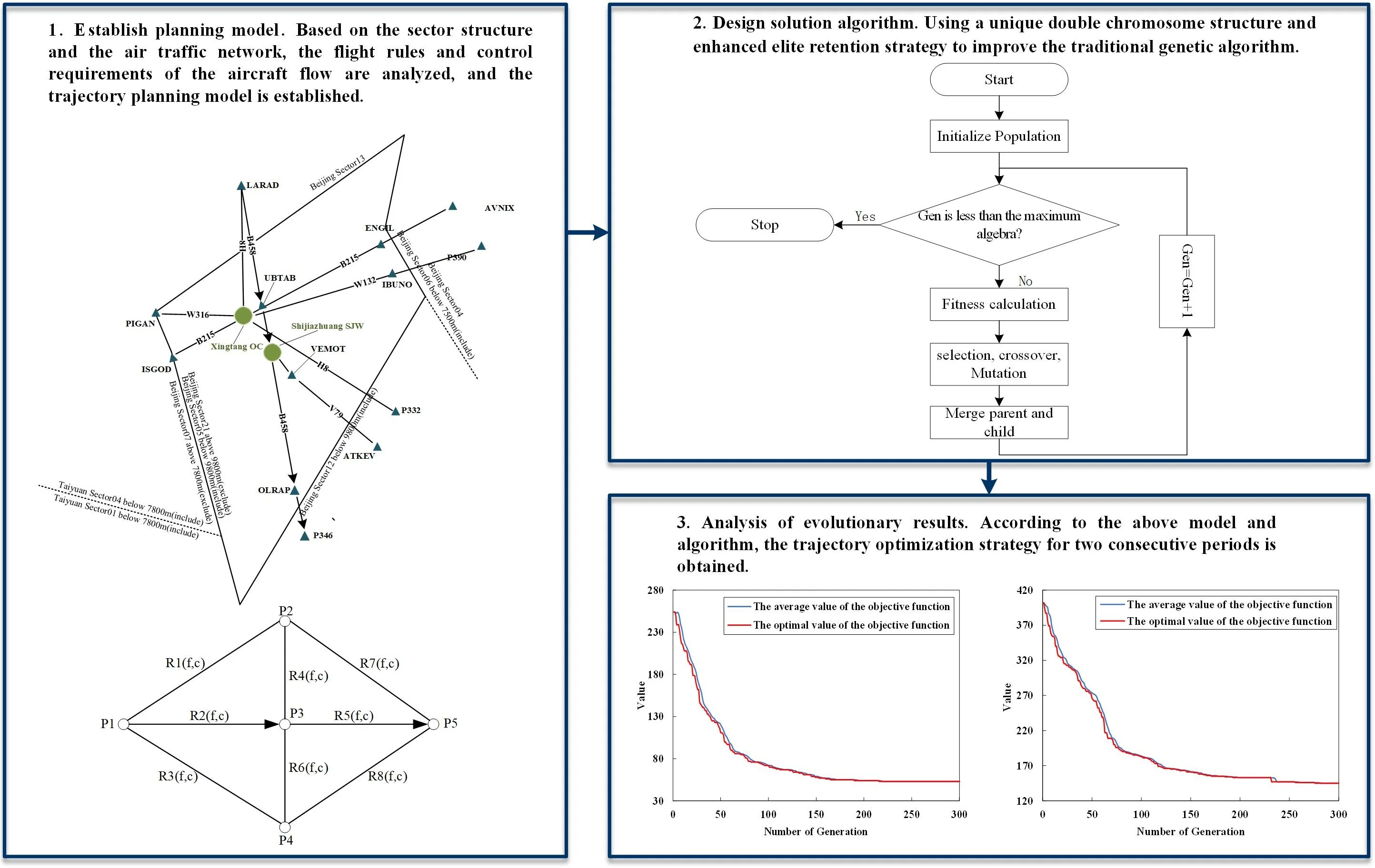
Airspace and airport capacity refers to the maximum number of aircraft sorties that an airspace and airport can receive in a specific period of time. The waypoints, routes and their capacity in the airspace constitute a weighted air traffic network directed graph, which thoroughly reflects the airspace operation status and restriction information. As shown in Fig. 1, $P$ is the waypoint; $R$ is the route; $f$ is the flow; and $c$ is the capacity. The conflict of capacity and flow in busy airspace sectors not only causes congestion in the air traffic network, but exposes a significant threat to the safety of the traffic flow. Aiming at resolving the airspace congestion problem caused by excessive traffic in the sector, this article takes the shortest entry delay as the optimization goal from a macro perspective, while constraints include the restrictions between capacity and flow, the minimum time interval between aircraft, along with the priority of the aircraft. Consequently, a 4DT planning model for continuous-period with the priority of aircraft is established, which is to program the sector entry time in continuous-period and reach the balance between capacity and flow in the airspace.

Fig. 1Schematic diagram of air traffic network

2.2. Basic assumptions

In order to describe the problem concisely and comprehensively, the following assumptions are established:

(1) Treat the aircraft as a mass point;

(2) Each aircraft enters the sector at the scheduled time;

(3) Both upstream and downstream sectors are in a state of balance between capacity and flow;

(4) The existing aircraft in the sector are not considered.

2.3. Model parameters

The symbol parameters used in the model are defined as shown in Table 1.

2.4. Optimization model

The objective function and constraint conditions of the model are shown in Eqs. (1-5):

Eq. (1) is the objective function, which indicates that the total delay of arrival of all aircraft in the two time periods is the smallest; Eq. (2) represents the balance constraint between capacity and flow, that is, within a time period, the flow in sector $S$ must be less than or equal to the capacity, and greater than or equal to μ times the capacity ($\mu$ is a constant, $\mu <$1), in order to ensure the flight safety of aircraft while not wasting airspace resources; Eq. (3) is the time interval constraint for the entry time, that is, for aircraft with the same entry waypoints, the sector entry time must meet the minimum time interval to avoid conflicts between aircraft; Eq. (4) means that the constraint of not arrived in advance, that is, the planned sector entry time of the aircraft cannot be earlier than the scheduled time; Eq. (5) is the flight priority constraint, that is, after the planning in the first stage $T_1$, the aircraft, whose entry time $t_{aa}^{\mathrm{\text{'}}}$ are within the second time period $T_2$, which means the planned time must be earlier than the other flights with the same entry waypoint.

2.5. Model solving

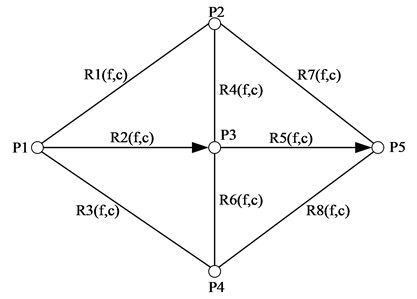
Due to the complex problems and constraints of the model in this article, a genetic algorithm with better search ability and convergence performance is selected to be implemented in the model. Genetic algorithm is a bionic algorithm for searching the optimal solution conceived based on the principle of biological evolution. It simulates the natural process of gene recombination and evolution, converts the parameters of the problem into genes through coding. Several genes form a chromosome, which is treated as an individual. A number of chromosomes experience natural selection, paired crossover and mutation. After multiple iterations, the most optimized result is obtained. In order to improve the optimization ability and reduce the runtime of the algorithm, this article improves the genetic algorithm and designs a dual-chromosome genetic algorithm with strategy of enhanced elitism preserving. The algorithm steps are shown in Fig. 2.

2.5.1. Encoding

Considering the complex constraints of the problem, this article chooses the real-valued encoding, calculates the scheduled entry time of each aircraft as the time difference compared to 00:00:00 of the day and converts it into minutes. This real value is expressed as a gene. In addition, the number of decision variables in the problem is large, so dual-stranded chromosomes that are more in line with diploid biological characteristics are designed, so that the decision variables are evenly distributed on two chromosomes, which are expressed as an individual. For example, there are 10 aircraft in the question, and their scheduled entry time are 08:00:00, 08:06:00, 08:10:00, 08:15:00, 08:04:00, 08:10:00, 08:16:00, 08:25:00, 08:20:00, 08:14:00, the dual-chromosome genotypes with real value encoding are shown in Table 2.

Table 2Dual-chromosome structure with real-valued encoding

X1	480	486	490	495	484
X2	490	496	500	505	494

Fig. 2Genetic algorithm steps

3.1. Algorithm running results

According to the historical flight data of North China in October 2018, the traffic flow of each sector was analyzed in the busy sector and period, and the data of the Beijing ACC05 sector on October 28, 2018, 16:00:00-17:00:00 was selected as the basis. The process of data preprocessing is shown in Table 3.

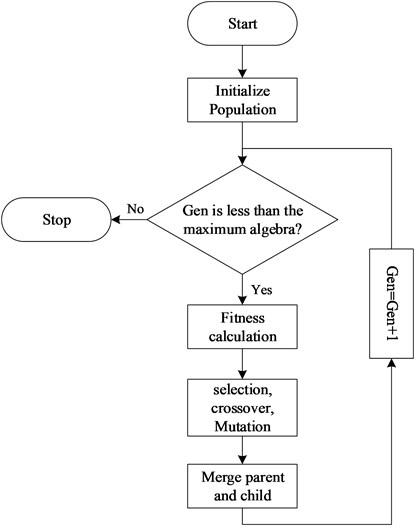
The selected period was divided into two consecutive periods, and the entry time of the aircraft which will enter the sector is planned. Specifically, 16:00:00-16:29:59 is the first time period $T_1$, and 16:30:00-17:00:00 is the second time period $T_2$. The sector structure of Beijing ACC05 is shown in Fig. 3: there are 7 important routes and 3 main entry points in the sector, named ISGOD, LARAD-B458-UBTAB, and ENGIL. According to the traffic capacity table in North China, the ACC05 sector has a half-hour capacity of 23 sorties. This article uses Python, combined with the third-party genetic algorithm toolbox Geatpy to programming the algorithm.

Fig. 3ACC05 sector structure diagram

In the genetic algorithm, the population size is set to 60 with the maximum evolutionary generation being 300. According to the optimization model and the improved genetic algorithm proposed in the article, the sector entry time of aircraft in a continuous period is planned. The final entry time optimization strategy and delay time of each aircraft are shown in Table 4.

In Table 4, there are 25 aircraft in the $T_1$ time period. After planning the entry time of the aircraft that enters the sector in the first time period, the entry time of the aircraft CHH7238, CSN6362, CSN3734 delays into the second time period. According to the principle to prioritize aircraft when the delay occurred, the entry time of these three aircraft must be earlier than other aircraft with the same entry way points in $T_2$ time period, to satisfy the timeliness requirements of aircraft operations. The optimization process of the entry time of the three aircraft with delays under the priority strategy is shown in the Table 5. As can be seen in Table 5, after the optimization of the priority strategy, the overall delay of the three flights has been reduced by 20 %.

The evolution results of genetic algorithm in the first time period $T_1$ and the second time period $T_2$ are shown in Fig. 4(a) and Fig. 4(b) respectively.

Fig. 4Algorithm evolution results

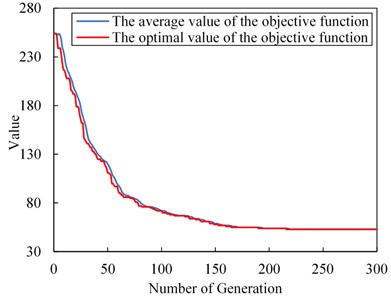
a) Results in $T_1$

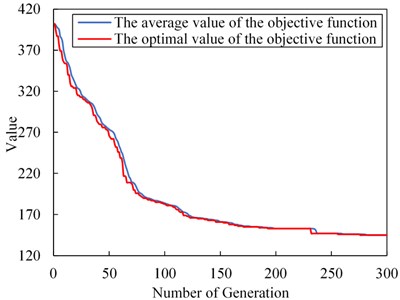
b) Results in $T_2$

It can be seen from Fig. 4(a) and Fig. 4(b) that the dual-chromosome genetic algorithm with enhanced elite retention strategy adopted in this article is stable in convergence. During the evolution of the solution in $T_1$ time period and the $T_2$ time period, although the optimal and average values of the individual objective function values of the population fluctuate, they have similar trends and generally show a downward trend, and both curves stabilized around the 230th generation. At this time, the optimal objective function value for the $T_1$ time period is 52, and the optimal objective function value for the $T_2$ time period is 157.

3.2. Algorithm comparison

In order to verify the optimization effect and the runtime of the algorithm, the algorithm is compared with the simple genetic algorithm. In the simple genetic algorithm, roulette wheel selection, partial matching crossover, and reverse transformation are used, with the population size is set to 60; the maximum evolutionary generation set to 300. The results are shown in Table 6.

Table 6 shows that in terms of the optimization effect, the algorithm reduces the delay time by 80.81 % and 62.72 % in the two time periods compared with the simple genetic algorithm. In terms of calculating speed, compared with the simple genetic algorithm, the algorithm in this article was 2.59 % and 36.36 % faster in the two time periods. Due to the limitation of the algorithm itself, the simple genetic algorithm produced a premature phenomenon in the process of solving this problem and fell into a local optimal solution. In summary, the dual-chromosome genetic algorithm with enhanced elite retention strategy adopted in this article has significant advantages in optimization effect and calculation speed. Simultaneously, it can provide an entry time strategy with the highest safety and the shortest delay time in a relatively short period of time, which can be applied to the current industry, in order to mitigate the risk of conflicts between aircraft, and improve the utilization of sector resources.