Optimizing and reliability analysis by firefly and genetic algorithms for a quadcopter

1.1. Background research

Reliability is an old concept and a new discipline, which has been the focus of engineers in many industries today for the development and improvement of quality. Reliability assessment methods in terms of the history of their origin, first in connection with the aerospace industry and during World War I. The second was done for German rockets in a preliminary way, but it was quickly noticed in other industries, such as the nuclear industry, which was under intense pressure to ensure the safety of nuclear reactors to provide electrical energy.

Several years after the United States launched its first satellite, statistical analyses of reliability and orbital failures were developed. In 1973, Krishna Behari Misra introduced the concepts of reliability and cost. The concept of reliability suggests many methods for optimal design of a system under certain conditions. In most of the articles, the main issue is assigning reliability to the components of the system and optimizing it based on bounded information. This process is a partial optimization for reliability. In the design phase, a designer has many options for system design. These options include increasing the reliability level of components and using extra components. A correct optimal system design examines all these options. Throughout the feasibility article Satisfying the optimal design is followed by cost constraints and the use of supporting components [6].

Kamal Kumar Govil investigated issues of partial reliability, discrete points of cost, and reliability. Also, placing these discrete data in a standard chart is necessary and vital. In this article, by using the least squares method, the crucial relationships of reliability and cost are expanded for use in problems with discrete data [7].

To increase reliability of series-parallel systems, plug-in components are used in the optimization plan, referred to as the redundancy allocation problem. In order to increase reliability concepts and components while taking into account limitations such as volume and weight, this problem aims to increase reliability concepts and components. The series-parallel structure is one of the types of system structures that is designed by allocating redundant components in parallel to the components of a system with a series structure [8].

Ku et al. stated in an article in 2000 that, in general, reliability can be defined as the long-term quality or the probability of a system's optimal performance under certain operational conditions in a certain period of time [9].

Zigo et al. designed a multi-objective optimization model for the reliability optimization problem through the allocation of additional components with transformation intensification. They solve the problem using a genetic algorithm [10].

In 2012, Joseph Homer Saleh et al. analyzed the reliability and failure of satellite electronic subsystems and their improvement through redundancy [11].

Additionally, in 2022, Tripti Dahiya et al. tried to improve the reliability of a system by combining two optimization algorithms, PSO and GA, in an article called Reliability optimization using hybrid genetic and particle swarm optimization algorithm [12].

Kazem Imani et. al. published a paper in 2022 in which they tried to calculate the reliability of a quadcopter power distribution [13].

1.2. Reliability indicators

The classic index of reliability, as mentioned, is the probability of failure, but many other indicators are also used for this purpose today, which depends on the type of system and their operational requirements, some of which are mentioned below [1, 14]: 1 – The number of expected failures in a certain time range. 2 – The average time between failures. 3 – Expected loss in investment due to failure. 4 – Expected reduction in system output due to various types of malfunctions. Each of these indicators can be evaluated using the relevant theory of reliability, and their selection will depend on the type of problem [15].

1.3. Types of system configuration

A system includes a network of components that are connected to each other in series, parallel, series-parallel combination and complex.

1.3.2. Parallel configuration

The combination of two or more components that are parallel to each other or, in other words, redundant members of each other, is called a parallel system. In this configuration, the system stops or crashes when all the components fail, and as long as at least one component performs optimally, the system will continue to work. System reliability $R_s\left(t\right)$ For $n$ parallel and independent components, it is obtained from the Eq. (2):

2

$R_s\left(t\right)=1-{\prod }_{i=1}^n\left(1-R_i\left(t\right)\right)\ge Max\left\{R_1\left(t\right),R_2\left(t\right),\dots ,R_n\left(t\right)\right\}.$

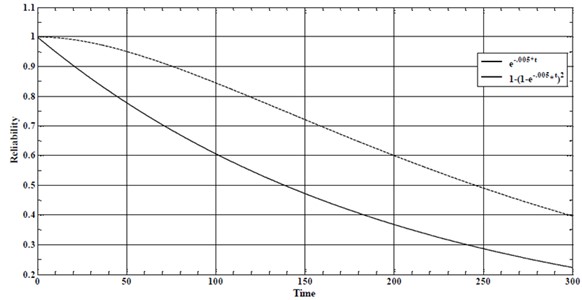
The reliability graph of the two supporting members is convex at the beginning of the time range. In comparison, the same graph for the single component is concave in the entire time range compared to the origin of the calculations. This difference is well shown in Fig. 1. In this figure, the failure rate for both modes, it is 0.005 per unit of time [1, 17, 18].

Fig. 1Reliability changes in parallel and single system

1.4. Combined series-parallel configuration

This system includes both series and parallel relationships between components. An example of a combined system is shown in Fig. 2.

Fig. 2Combined series-parallel configuration

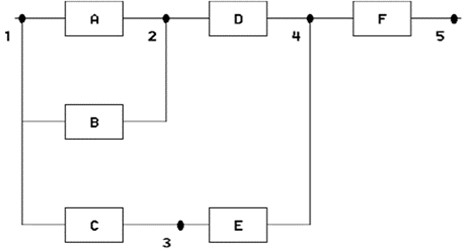
To calculate the reliability of the system, the network is broken into several sets, then the reliability of each set is calculated, and then the reliability of the system is obtained from the relationship of the reliability values of each set. In Fig. 7, the reliability is calculated as follows [3, 18]:

2.1. Reliability prediction

Special relationships are used to predict the failure rate of components or systems correctly. These relationships have been developed with statistical models and based on environmental parameters affecting the performance of components. Two crucial standards, NSWC-98/LEI for mechanical parts and MIL HNBK- 217 for electronic components and the IEC-62380 document, have fully expanded these relationships. In this project, the MIL HNBK-21 standard and the IEC-62380 document have advanced the reliability plan.

2.2. Calculating quadcopter reliability

In calculating the reliability, estimating the failure rate of parts is very important. Calculating this number is very expensive for companies producing parts due to the complexity and variety of lifetime tests. As a result, in most cases, the failure rate of parts is not recorded in their information table. This makes it difficult to calculate the reliability of the quadcopter. To overcome this problem, alternative methods are used to calculate the failure rate of these parts. One of these methods, which is used for electronic parts, is reliability prediction based on models. Statistics have expanded. Another method is the method of assigning reliability to each of the components, which is achieved according to the influencing parameters of a system, including complexity, technology, environmental conditions, and performance time. Here we consider the operational life of the quadcopter as 3 years [19, 20].

2.3. Optimization methods

Optimization methods and algorithms are divided into two categories: exact and approximate algorithms. Approximate algorithms are divided into two categories: heuristic and meta-heuristic algorithms. In the exact method, we have a series of algorithms that can give a completely accurate and definitive answer by searching and viewing all the data. These algorithms have low speed and naturally, they are not very useful for problems with large data and dimensions. On the other hand, in the approximate method, there are another series of algorithms that can search specific parts of the data by using the initiative, and by doing so, they increase the speed of generating the answer. Although, this is heuristic algorithms do not guarantee that the obtained answer is the best possible answer. That is, if you search further, you will probably find a better answer. The biggest problem of the heuristic method is that it needs to know the problem. In other words, an innovative algorithm will be responsible for a specific problem. Another problem of heuristic algorithms is their getting stuck in local optimal points, and premature convergence to these points, and here another series of algorithms have been created that can search for optimal points without having the problems of heuristic methods. Indeed, meta-heuristic algorithms are able to solve the problem with reasonable speed and accuracy by providing a general solution without knowing the problem. These methods are in the term independent of the problem [5].

2.4. Problem statement

The firefly algorithm is a new population-based multivariate approach developed by Xin-She Yang and inspired by the behavior of the blinking properties of fireflies. The flickering light can be formulated in such a way that it is accompanied by an optimized objective function, which enables the formulation of the firefly algorithm. To implement this algorithm for a board, we consider a quadcopter that includes six main components, each component is marked with a number as follows. For this purpose, we consider four main components and each index represents one of the components. These are the four components in order: 1 – flash memory, 2 – driver, 3 –transmitter and receiver, 4 – processor, 5 – flow sensor, 6 – temperature sensor.

In this problem, the weight function, the cost function, and the objective function are known, and the relationships and correlations between them are known. We should get the most optimal mode for reliability by running the program and determining the different modes of redundancy in order to have the most optimal mode according to the weight and cost limitations. In this case, the maximum weight is 5000 grams and the maximum cost is 3500 dollars. Next, in order to validate the firefly program, we implement this program in Toolbox Optimization of MATLAB software by genetic algorithm and compare the results.

Fig. 3Algorithm of the FA

The reliability-redundancy assignment problem to maximize the system reliability by considering the constraints can be formulated as follows:

In this research, we are looking for multi-objective optimization. We want to have maximum reliability with minimum cost and weight for our quadcopter. The following function should be maximized $R_s=f\left(r,n\right).$Also considering $1\le i\le m$, $n_i\in Z^{+}$, $g\left(r,n\right)\le 1$, $0\le r_i\le 1$, $r_i\in R$ where in$R_s$. Subsystem reliability, g are a set of constraint functions (weight and cost functions), $r=(r_1{,r}_2{,r}_3,\dots$). Reliability vector of subsystem components and $n=\left(n_1{,n}_2{,n}_3,\dots \right)$ are the vector of redundancies assigned to the subsystem. $r_i$ and $n_i$. The reliability and number of components of each subsystem is in the $i$-th component of the subsystem. For example, $n_1$ The total number of flash memory (main + spare) and $r_1$. The amount of reliability of flash memory. $f\left(0\right).$The objective function for all reliability of the subsystem, l is the resource limitation of the subsystem and m is the number of components of each member in the subsystem. This problem is a series of mixed-integer nonlinear problems. The problem can be started as follows:

The function $f\left(r,n\right)=\prod _{i=1}^m\left[1-{\left(1-r_I\right)}^{n_i}\right]$ should be maximized. Considering the weight function $g_1\left(r,n\right)=\sum _{i=1}^m{w}_i{n}_i^2{e}^{0.25n_i}\le W$, and cost function, $g_2\left(r,n\right)=\sum _{i=1}^{m}C\left(r_i\right){[n}_i{e}^{0.25n_i}]\le C$, where in $1\le n_i\le 6$ and $r_i\in R$ and $0.5\le r_i\le 0.999999$ and $n_i\in Z^{+}$ and $C$ the limit of the cost (budget). Here, $i$ is the desired part number in the subsystem. For example, $n_1$ represents the total number of flash memories (main + surplus) and$r_1$ indicates the reliability of flash memories with the number considered $C\left(r_i\right)=a_i.{\left[\frac{-T}{\mathit{ln}\left(r_1\right)}\right]}^{b_i}$ is the component cost function where $T$ is the operating time of each subsystem component in which it does not fail. $W$ is also an upper limit of the weight of the subsystem. It’s derived from the fault tree analysis of the subsystems’ structure diagrams. Since the attractiveness of a firefly is proportional to the intensity of light seen by neighboring fireflies, we can now define the attractiveness $\beta$ of a firefly in terms of the Cartesian distance between firefly $i$ and firefly $j$. In this case, the distance of the $i$-th firefly to the more attractive (brighter) $j$-th firefly that is attracted to it, is Eq. (3):

The second part is related to the attractiveness of fireflies, where${\beta }_0$ is the absorption coefficient of fireflies, absorption coefficient in $r=0$. In the third part, we are looking to create random numbers using the $\alpha$ coefficient. The generated random number is between 0 and 1.

2.5. Structure of the manuscript

In the continuation of the Results section, it is divided into two sections: component reliability calculation and optimization section. In the reliability section, we examine the components of the quadcopter and calculate the reliability of the various parts of the quadcopter using the failure rate and existing relationships and tables.

Next, in the optimization section, we will first explain the parameters and the algorithm, and then we will express the results of the firefly algorithm. Finally, we use the genetic algorithm to validate the result of the firefly algorithm.

In the Conclusion section, we have compared the results of firefly and genetics algorithms and we have displayed the results of the comparison under the title of Table 9.

3.1. Reliability

3.1.2. Reliability estimation of printed circuit fiber and connections

3.1.2.1. Estimating the reliability of connections

The reliability between the board and the components are sensitive to heat and the type of connections. The sensitivity can be expressed in the form of Eq. (4) [19], [25], [26]:

4

${\lambda }_{Fibr}=(1+3\times {10}^{-3}\times \left[{\sum }_1^j{\left({\pi }_n\right)}_i\times {\left({∆T}_i\right)}^{0.68}\right]\times \sum {\lambda }_d.$

Table 3Connections on board [25-27]

Effective coefficient ${\left({\mathrm{\pi }}_{\mathrm{n}}\right)}_{\mathrm{i}}$	${\mathrm{n}}_{\mathrm{i}}\le$8760 Cycles/Year		${\left({\mathrm{\pi }}_{\mathrm{n}}\right)}_{\mathrm{i}}={\mathrm{n}}_{\mathrm{i}}^{0.76}$
	${\mathrm{n}}_{\mathrm{i}}>$ 8760 Cycles/Year		${\left({\mathrm{\pi }}_{\mathrm{n}}\right)}_{\mathrm{i}}=1.7{\mathrm{n}}_{\mathrm{i}}^{0.6}\mathrm{}$
${\mathrm{n}}_{\mathrm{i}}$: Number of cycles including turning the board off and on in a year with temperature range of $\mathrm{\Delta }{\mathrm{T}}_{\mathrm{i}}$
$\mathrm{\Delta }{\mathrm{T}}_{\mathrm{i}}={\left({\mathrm{T}}_{\mathrm{a}\mathrm{c}}\right)}_{\mathrm{i}}-{\left({\mathrm{T}}_{\mathrm{a}\mathrm{e}}\right)}_{\mathrm{i}}$			$\mathrm{\Delta }{\mathrm{T}}_{\mathrm{i}}$
${\left({\mathrm{T}}_{\mathrm{a}\mathrm{c}}\right)}_{\mathrm{i}}$: Outdoor environment temperature in the $\mathrm{i}$th phase of operation		${\left({\mathrm{T}}_{\mathrm{a}\mathrm{e}}\right)}_{\mathrm{i}}$: Indoor environment temperature, near the components in the $\mathrm{i}$th phase of operation
For solder joints in each 1 billion hours equal 0.5		${\mathrm{\lambda }}_{\mathrm{d}}$

Due to the small space of the board and box, the temperature of the environment near the components is the same as the temperature around the board. As a result, the failure rate and reliability of connections are:

${\lambda }_{Fibr}=\left(1+3\times {10}^{-3}\times \left[1\times {\left(27-3\right)}^{0.68}\right]\right)\times 766\times 0.5\times {10}^{-9}=3.92\times {10}^{-7}\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$h$}\right.,$
$R=e^{-\lambda t}=e^{-3.92\times {10}^{-7}\times 365\times 2\times 24}=0.9931.$

The reliability of a printed circuit fiber depends on the area of the fiber openings, the number of circuit layers, the width of the signal path on the board and the number of connections:

5

${\lambda }_{Fibr}=5\times {10}^{-12}\times {\pi }_T\times {\pi }_C\times \left[N_t\sqrt{1+\frac{N_t}{S}}+N_P\times \frac{1+0.1\sqrt{s}}{3}\times {\pi }_L\right]$
$\times \left(1+3\times {10}^{-3}\times \left[{\sum }_1^j{\left({\pi }_n\right)}_i\times {\left(∆T_i\right)}^{0.68}\right]\right).$

Coefficients and impact factors can be calculated using the Table 4.

Table 4Effective coefficients and factors in calculating the reliability of printed circuit fiber [27]

Effective coefficient ${\pi }_c$	Number of Layers ≤ 2	${\pi }_c=$1
	Number of Layers > 2	${\pi }_c=$ 0.7 × $\sqrt{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{}\mathrm{o}\mathrm{f}\mathrm{}\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{s}}$
$N_p$: Number of Signal Paths $N_t$: Number of holes in the board $S$: Board Area (120 cm2)
${\pi }_t=e^{1740\left(\frac{1}{303}\frac{1}{273+t_A}\right)}$
0.56	0.35	0.23	0.15	0.1	Width of the maximum flow path
1	2	3	4	5	${\pi }_L$

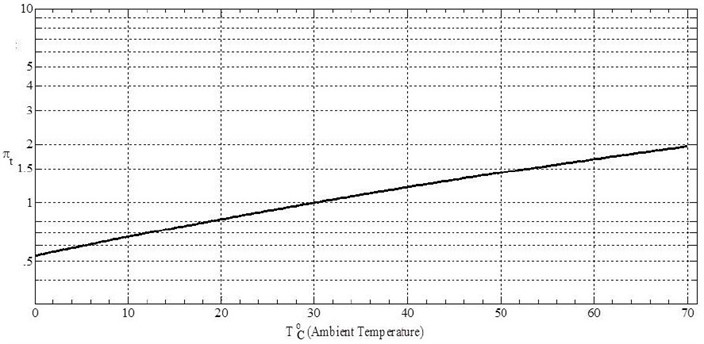
For the proper analysis of the temperature coefficient, the maximum temperature of the device must be taken into account, and for this purpose, the diagram in Fig. 4 is used:

${\pi }_t=e^{1740\left(\frac{1}{303}-\frac{1}{273+13}\right)}=0710.$

The fiber printed circuit board for the control board has 19 apertures, including embedded apertures for screws, connecting parts and connectors. Also, there are 53 signal paths in all layers of the board to connect different parts. According to Eq. (5):

${\lambda }_{PCB}=5\times {10}^{-12}\times 0.710\times 1\times \left[19\times \sqrt{1+\frac{19}{90}}+53\times \frac{1+0.1\sqrt{90}}{3}\times 3\right]\times 1.0260=6.801\times {10}^{-9}\frac{f}{h}.$

Finally, the reliability of printed circuit fiber is equal to:

$R_{Fibr}=e^{-\lambda t}=e^{-3.801\times {10}^{-9}\times 365\times 24}=0.94946346.$

Fig. 4Temperature factor changes in the range of 0-70 degrees Celsius

3.2. Optimization

4.1. Limitation

In this research, we were faced with limitations in obtaining the failure rate of some parts, and with great effort, we succeeded in obtaining their values.

4.2. Recommendations

In future researches, other optimization algorithms can be investigated and the results compared with the results of the current research. Also, other UAVs can be investigated in terms of reliability and risk management.

Therefore, by comparing the obtained answers, we can say that due to the closeness of the answers, we can ensure the correctness of the answers of the firefly algorithm.