Vibration influence of different types of heavy-duty trucks on road surface damage

Under the interaction of the wheels of heavy-duty trucks on the random road surface when the vehicles are travelling, their generated vibrations not only affect the driver's ride comfort but also impact the road surface damage. To assess the vibration influence of different types of vehicles on the road surface damage, three dynamic models of the two axle, three axle, and four axle of heavy trucks have been build and computed via the Matlab/Simulink software. The dynamic tire load, dynamic load coefficient, and dynamic load-stress factor are chosen to assess the friendly load of different heavy trucks under the different operating conditions of the vehicle. The obtained result indicates that the dynamics parameters including suspension system, tires, and axle load distributions of heavy trucks have a greater effect on the dynamic tire force than the total weight of the vehicle. In order to ensure the road’s safety, the traffic management should intervene quickly to give a velocity limit for vehicles under the condition of the vehicle moving with the empty loaded on the poor road surface.

Vibration influence of different types of heavy-duty trucks on road surface damage

Highlights

Three dynamic models of the two axle, three axle, and four axle of heavy trucks have been build to assess the vibration influence of different types of vehicles on the road surface damage.
The dynamics parameters including suspension system, tires, and axle load distributions of heavy trucks have a greater effect on the dynamic tire force than the total weight of the vehicle.
To ensure the road's safety, the traffic management should intervene quickly to give a velocity limit for vehicles under the condition of the vehicle moving with the empty loaded on the poor road surface.

1. Introduction

Nowadays, the heavy trucks play an important role in the transportation of goods for economic development. Therefore, the road surface damage and decrease of the ride comfort was mainly caused by the vehicle's loads in the traveling condition [1-4]. A dynamic model of the heavy truck using 5-axle of the wheels was established to analyze the influence of the speeds, random road surface, suspension systems, and wheel systems of the heavy vehicle on the minimal vertical dynamic load factor, the maximal vertical dynamic load factor, and the dynamic load stress factor [3]. Besides, based on multi-body dynamic theory for heavy-duty vehicles, a vehicle dynamic model was also established to evaluate the effect of the operating parameters of the speeds, loads, random road surfaces, and stiffness of the wheel on the dynamic loads and the dynamic load coefficients (DLC) of the wheels [1, 5-7]. Moreover, in order to reduce the dynamic tire load acting on the road surface, the design parameters of suspension systems of the heavy truck were also optimized [8, 9] and controlled based on the genetic algorithm and optimal control theory [10-14]. In addition, to reduce the excitation force between the wheel and random road surface, a 3-D vehicle-pavement coupled model to simulate the pavement dynamic loads induced by the vehicle-pavement interaction where both vehicle vibration and pavement deformation were considered. The effect of road surface conditions, vehicle parameters, and driving speed on the pavement dynamic loads were then analyzed. The impact factor, dynamic load coefficient, and frequency distribution of pavement loads were used to evaluate their impaction on the road-friendliness [2, 5]. However, these above studies mainly evaluated the effect of the wheel and road surface interaction of a heavy truck.

In reality, there are many different types of heavy trucks including two-axle vehicle, three-axle vehicle, four-axle vehicle, five-axle vehicle, and more axle vehicle; and the heavy vehicles running on the national highways increase not only the number of vehicles but also the vehicle load which are the major causes of road damage. Therefore, the major goal of this study is to establish the vibration model of the different heavy trucks for determining the dynamic wheel loads. A dynamic load-stress factor is used to evaluate the influence of the dynamic wheel loads on the highway road surface. Matlab/Simulink is used to simulate the vehicle vibration models and calculate the impact factors. From the vibration model, dynamic loads of the wheel, DLC, and dynamic load-stress factor are analyzed under the different vehicle speeds, vehicle loads, and road surface roughness, respectively.

2. Dynamics model of different heavy trucks

2.1. Vehicle’s dynamic model

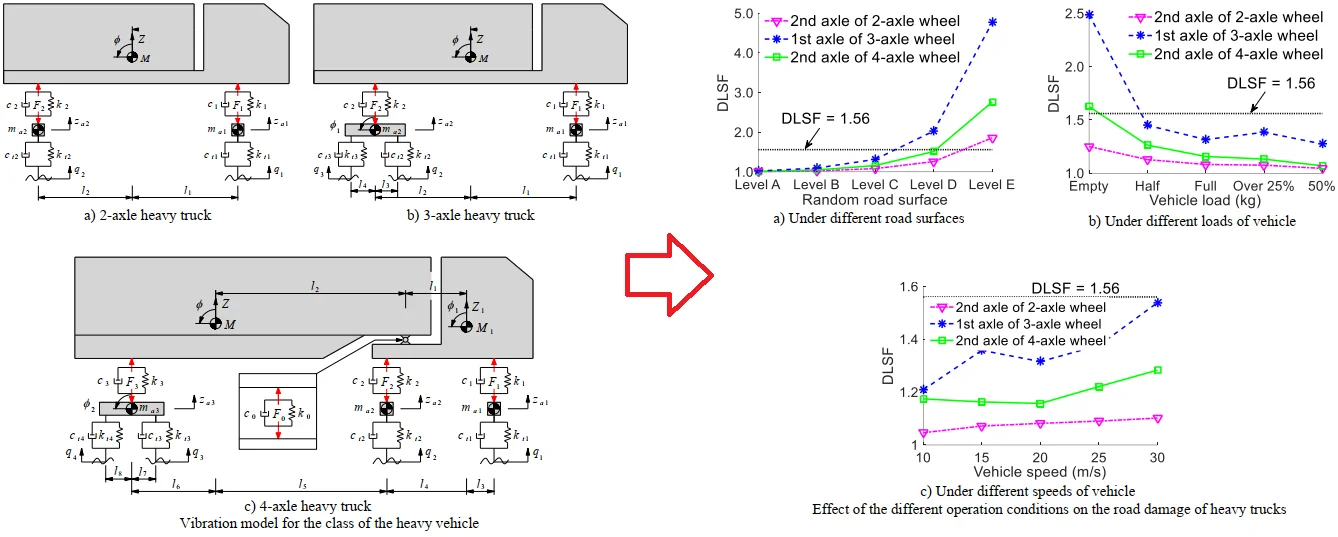
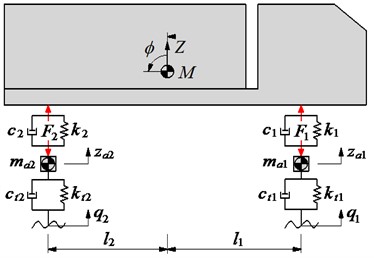
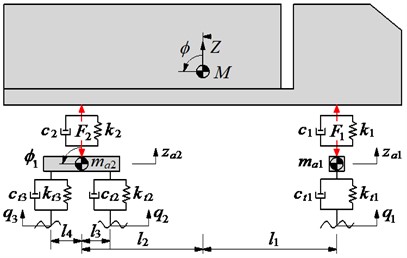
Three types of heavy trucks including two-axle vehicle, three-axle vehicle, and four-axle vehicle are chosen to evaluate the influence of the vibration of heavy trucks on road damage. The dynamic model of the heavy trucks with multiple degrees of freedom is built in Fig. 1, where $M$ and $M_{1}$ are the sprung mass of the heavy trucks (tractor and trailer); $m_{a 1}$ , $m_{a 2}$ , and $m_{a 3}$ are the unsprung mass of the front axle, the rear axle, and the tandem axle, respectively; $k_{1 - 3}$ and $c_{1 - 3}$ are the stiffness and damping coefficients of the suspension systems; $k_{t 1 - t 3}$ and $c_{t 1 - t 3}$ are the stiffness and damping coefficients of the wheels; $Z$ and $Z_{1}$ are the displacements of the sprung mass of the heavy trucks (tractor and trailer); $ϕ$ and $ϕ_{1}$ are the pitching angle of the sprung mass of the heavy trucks (tractor and trailer); $z_{a 1 - a 3}$ is the vertical displacements at the centre gravity of the axles; and $l_{1 - 8}$ is the distance of the vehicle.

Fig. 1Vibration model for the class of the heavy vehicle

a) 2-axle heavy truck

b) 3-axle heavy truck

c) 4-axle heavy truck

2.2. Different vibration equations

To facilitate the description of the vehicle’s vibration via the computer simulation, a combined method of the multi-body system theory and D’Alembert’s principle is chosen to calculate the vibration equation of the heavy trucks. The multi-body system theory is used to separate the system into subsystems which are linked by the force and moment equations. D’Alembert’s principle is used to set up force and moment equations to describe the dynamic subsystems of the heavy trucks in Fig. 1 as follows.

The vibration equation of a 2-axle heavy truck:

1

\{\begin{array}{l} M \ddot{Z} = F_{1} + F_{2}, \\ I \ddot{ϕ} = F_{1} l_{1} - F_{2} l_{2}, \end{array} \{\begin{array}{l} m_{a 1} {\ddot{z}}_{a 1} = F_{t 1} - F_{1}, \\ m_{a 2} {\ddot{z}}_{a 2} = F_{t 2} - F_{2}, \end{array}

where the force responses of the suspension systems of the vehicle and wheels of $F_{1,2}$ and $F_{t 1, t 2}$ are determined as in Eq. (2):

2

\{\begin{array}{l} F_{i} = k_{i} [z_{a i} - Z + (- 1)^{i} l_{i} ϕ] + c_{i} [{\dot{z}}_{a i} - \dot{Z} - (- 1)^{i} l_{i} \dot{ϕ}], \\ F_{t i} = k_{t i} (q_{i} - z_{a i}) + c_{t i} ({\dot{q}}_{i} - {\dot{z}}_{a i}), i = 1,2 . \end{array}

The vibration equation of a 3-axle heavy truck:

3

\{\begin{array}{l} M \ddot{Z} = F_{1} + F_{2}, \\ I \ddot{ϕ} = F_{1} l_{1} - F_{2} l_{2}, \\ m_{a 1} {\ddot{z}}_{a 1} = F_{t 1} - F_{1}, \end{array} \{\begin{array}{l} m_{a 2} {\ddot{z}}_{a 2} = F_{t 2} + F_{t 3} - F_{2}, \\ I_{1} {\ddot{ϕ}}_{1} = F_{t 2} l_{3} - F_{t 3} l_{4}, \end{array}

where the force responses of the suspension systems of the vehicle and wheels of $F_{1,2}$ and $F_{t 1 - t 3}$ are determined as in Eq. (4):

4

\{\begin{array}{l} F_{i} = k_{i} [z_{a i} - Z + (- 1)^{i} l_{i} ϕ] + c_{i} [{\dot{z}}_{a i} - \dot{Z} + (- 1)^{i} l_{i} \dot{ϕ}], i = 1, 2, \\ F_{t 1} = k_{t 1} (q_{1} - z_{a 1}) + c_{t 1} ({\dot{q}}_{1} - {\dot{z}}_{a 1}), \\ F_{t j} = k_{t j} [q_{j} - z_{a 2} + (- 1)^{j + 1} l_{j + 1} ϕ_{1}] + c_{t j} [{\dot{q}}_{j} - {\dot{z}}_{a 2} + (- 1)^{j + 1} l_{j + 1} {\dot{ϕ}}_{1}], j = 2, 3 . \end{array}

The vibration equation of a 4-axle heavy truck:

5

\{\begin{array}{l} M_{1} {\ddot{Z}}_{1} = F_{1} + F_{2} - F_{0}, \\ I_{1} {\ddot{ϕ}}_{1} = F_{1} l_{3} + F_{0} l_{1} - F_{2} l_{4}, \\ M \ddot{Z} = F_{0} + F_{3}, \\ I \ddot{ϕ} = F_{0} l_{2} - F_{3} l_{6}, \end{array} \{\begin{array}{l} m_{a 1} {\ddot{z}}_{a 1} = F_{t 1} - F_{1}, \\ m_{a 2} {\ddot{z}}_{a 2} = F_{t 2} - F_{2}, \\ m_{a 3} {\ddot{z}}_{a 3} = F_{t 3} + F_{t 4} - F_{3}, \\ I_{2} {\ddot{ϕ}}_{2} = F_{t 3} l_{7} - F_{t 4} l_{8}, \end{array}

where the force responses of the suspension systems of the vehicle and wheels of $F_{0}$ , $F_{1 - 3}$ , and $F_{t 1 - t 4}$ are determined as in Eq. (6):

6

\{\begin{array}{l} F_{i} = k_{i} (z_{a i} - Z_{i}) + c_{i} ({\dot{z}}_{a i} - {\dot{Z}}_{i}), i = 1, 2, 3, \\ F_{t j} = k_{t j} (q_{j} - z_{a j}) + c_{t j} ({\dot{q}}_{j} - {\dot{z}}_{a j}), j = 1, 2, 3,4, \\ F_{0} = k_{0} (Z_{1} - l_{1} ϕ_{1} - Z - l_{2} ϕ) + c_{0} ({\dot{Z}}_{1} - l_{1} {\dot{ϕ}}_{1} - \dot{Z} - l_{2} \dot{ϕ}) . \end{array}

The differential Eqs. (1), (3), and (5) are given by the following matrix form:

7

M \ddot{Z} + C \dot{Z} + K Z = C_{t} \dot{Q} + K_{t} Q,

where $M$ , $C$ , $K$ , $C_{t}$ , and $K_{t}$ are the mass matrix of the heavy truck, damping and stiffness matrix of the suspension systems, and damping and stiffness matrix of the wheels, respectively; $Z$ is the displacement vector, and $Q$ is the vibration excitation vector of the road surface.

2.3. Vibration excitation sources

The roughness of the highway road surface greatly affects the interaction between the wheel and road surface and the road damage. It plays an important role in evaluating dynamic interaction between vehicles and roads. The excitation of the random road surface is represented with a random process. The equation of the power spectrum density (PSD) of the random road is expressed as follows [8, 15]:

8

S_{q} (n) = S_{q} (n_{0}) {(\frac{n}{n_{0}})}^{- ω},

where $n$ is the wavelength’s reciprocal space frequency; $n_{0}$ is the reference space frequency, ( $n_{0} =$ 0.1 m^–¹); $S_{q} (n)$ is the PSD of road surface under the reference space frequency $n_{0}$ known as the road surface roughness coefficient; and $ω$ is the frequency index that decides the frequency configuration of PSD of road surface ( $ω =$ 2).

The road surface roughness is assumed to be a zero-mean stationary Gaussian random process. It can be generated through an inverse Fourier transformation:

9

q = \sum_{i = 1}^{N} \sqrt{2 S_{q} (n_{i}) Δ n} c o s (2 π n_{k} t + ϕ_{i}),

where $ϕ_{i}$ is the random phase uniformly distributed from 0 to 2 $π$ .

According to the standard ISO 8068 [15], five types of typical road surface roughness from ISO level A to E are applied to evaluate the road damage of heavy trucks. The simulation result of the typical road surface roughness from ISO level A to E is shown in Fig. 2.

Fig. 2The vibration excitation of the road surface roughness from ISO level A to E

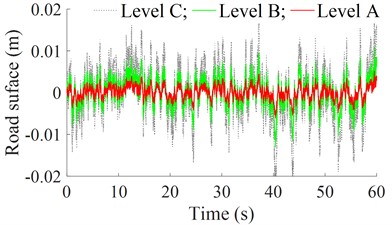
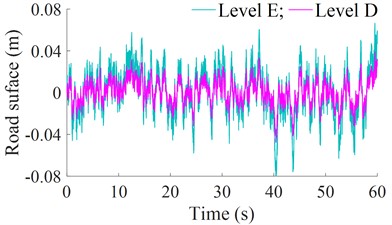
3. The damage index of road

Based on the existing research, the damage index of the road surface was evaluated based on the index of the dynamic load-stress factor (DLSF) [16, 17]. This index was calculated based on the road damage criteria is used to quantify the road load caused by dynamic road-tire forces. The DLSF value is given by [16, 17]:

10

D L S F = 1 + 6 D L C^{2} + 3 D L C^{4},

where $D L C = F_{t, R M S} / F_{s}$ is defined as the dynamic load coefficient of the wheel-road surface interaction, $F_{t, R M S}$ is the root mean square of the vertical dynamic load of the wheel, and $F_{s}$ is the static load of the wheel [1, 2, 6].

The DLSF is strongly dependent on the vehicle’s design parameters as well as the operating conditions of the vehicle. According to Refs. [1, 14], if the DLSF ≤ 1.56, this means that the road-friendly limit for the dynamic parameters of a vehicle and the operation conditions of the vehicle will be established.

4. Simulation result and evaluation

To compute the differential equations in Eqs. (1), (3), and (5) for evaluating the influence of the dynamic load of the heavy truck on the road damage of the highway road surface, based on the design parameters of all the heavy trucks listed in Tables 1, 2, and 3, Matlab/Simulink software is used to simulate and calculate the results under the condition of the heavy trucks is moving on the random road surface of the ISO level C at 72 km/h.

Table 1The design parameters of two-axle heavy truck

Parameter	Value	Parameter	Value	Parameter	Value
$M$ (kg)	6451	$k_{2}$ (N/m)	1.138×10⁶	$k_{t 2}$ (N/m)	0.876×10⁶
$m_{a 1}$ (kg)	297	$c_{1}$ (Ns/m)	15.00×10³	$c_{t 1}$ (Ns/m)	2.00×10³
$m_{a 2}$ (kg)	524	$c_{2}$ (Ns/m)	15.00×10³	$c_{t 2}$ (Ns/m)	2.00×10³
$k_{1}$ (N/m)	0.198×10⁶	$k_{t 1}$ (N/m)	0.788×10⁶	$l_{1}$ , $l_{2}$ (m)	3.79, 2.31

Table 2The design parameters of three-axle heavy truck

Parameter	Value	Parameter	Value	Parameter	Value
$M$ (kg)	7730	$c_{2}$ (Ns/m)	66.88×10³	$c_{t 3}$ (Ns/m)	3.00×10³
$m_{a 1}$ (kg)	561	$k_{t 1}$ (N/m)	1.00×10⁶	$l_{1}$ (m)	3.79
$m_{a 2}$ (kg)	899	$k_{t 2}$ (N/m)	1.00×10⁶	$l_{2}$ (m)	2.31
$k_{1}$ (N/m)	7.35×10⁶	$k_{t 3}$ (N/m)	1.00×10⁶	$l_{3}$ (m)	0.86
$k_{2}$ (N/m)	2.056×10⁶	$c_{t 1}$ (Ns/m)	3.00×10³	$l_{4}$ (m)	0.86
$c_{1}$ (Ns/m)	4.55×10³	$c_{t 2}$ (Ns/m)	3.00×10³

Table 3The design parameters of four-axle heavy truck

Parameter	Value	Parameter	Value	Parameter	Value
$M$ (kg)	12460	$c_{2}$ (Ns/m)	10.0×10³	$c_{t 4}$ (Ns/m)	3.00×10³
$M_{1}$ (kg)	2659	$c_{3}$ (Ns/m)	84.0×10³	$l_{1}$ (m)	2.712
$m_{a 1}$ (kg)	400	$c_{0}$ (Ns/m)	200×10³	$l_{2}$ (m)	4.843
$m_{a 2}$ (kg)	553	$k_{t 1}$ (N/m)	1.03×10⁶	$l_{3}$ (m)	0.778
$m_{a 3}$ (kg)	792	$k_{t 2}$ (N/m)	2.06×10⁶	$l_{4}$ (m)	2.712
$k_{1}$ (N/m)	2.32×10⁶	$k_{t 3}$ (N/m)	2.06×10⁶	$l_{5}$ (m)	2.131
$k_{2}$ (N/m)	8.60×10⁶	$k_{t 4}$ (N/m)	2.00×10⁶	$l_{6}$ (m)	2.357
$k_{3}$ (N/m)	2.00×10⁶	$c_{t 1}$ (Ns/m)	3.00×10³	$l_{7}$ (m)	0.50
$k_{0}$ (N/m)	20.0×10⁶	$c_{t 2}$ (Ns/m)	3.00×10³	$l_{8}$ (m)	0.50
$c_{1}$ (Ns/m)	2.20×10³	$c_{t 3}$ (Ns/m)	3.00×10³

Under the full load condition of the heavy trucks, the simulation and calculation results of the $F_{t, R M S}$ , DLC, and DLSF of the heavy trucks have been listed in Table 4. The calculation results show that the $F_{t, R M S}$ at 2nd axle of the 2-axle vehicle, 1st axle of the 3-axle vehicle, and 2nd axle of the 4-axle vehicle has the maximum value. Their dynamic load responses have been plotted in Fig. 3.

These results are similar to the results in Refs. [1, 14]. Under the influence of the maximum dynamic load of the wheel acting on the road surface of the heavy truck, both the values of DLC and DLSF at 2nd axle of the two-axle vehicle, 1st axle of the three-axle vehicle, and 2nd axle of the four-axle vehicle are also maximum. This means that the dynamic load of the wheel at 2nd axle of the two-axle vehicle, 1st axle of the three-axle vehicle, and 2nd axle of the four-axle vehicle greater affects the road damage than other axles of heavy trucks. Besides, the results of the DLC and DLSF in Table 4 also show that the values of DLC and DLSF at 1st axle of the three-axle vehicle are higher than that of 2nd axle of the two-axle vehicle and 2nd axle of the four-axle vehicle. This means that the vehicle's design parameters such as suspension systems, tires, and axle load distribution have a greater effect on the dynamic tire load than the total weight of the vehicle. However, this study will focus on analyzing the influence of the operation conditions of heavy trucks on the DLSF and this problem will be continued to discuss in the following section.

Table 4Different dynamic loads at the axles of the different heavy trucks

Parameter	Axle location	Heavy trucks
Parameter	Axle location	2-axle vehicle	3-axle vehicle	4-axle vehicle
$F_{t, R M S}$ (N)	1st axle	1734.8	7747.3	14.173
	2nd axle	5172.9	3528.4	19.006
	3rd axle		3529.8	8.882
	4th axle			9.044
DLC	1st axle	0.0645	0.2264	0.1608
	2nd axle	0.1163	0.1262	0.1619
	3rd axle	–	0.1262	0.0902
	4th axle	–	–	0.0918
DLSF	1st axle	1.0250	1.3154	1.1571
	2nd axle	1.0818	1.0963	1.1593
	3rd axle	–	1.0963	1.0490
	4th axle	–	–	1.0508

Fig. 3Maximum dynamic load of the wheel axle acting on the road surface

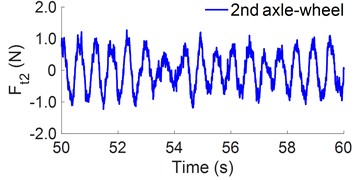
a) 2-axle heavy truck

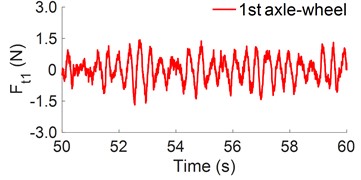
b) 3-axle heavy truck

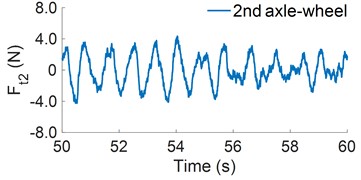
c) 4-axle heavy truck

4.1. Under the different road surfaces

The road surface roughness not only affects the ride comfort as well as the durability of the part of heavy trucks but also affects the dynamic wheel load. To analyze the effect of the road surface roughness on the DLSF, five types of the random road of ISO level A to ISO level E are simulated when heavy trucks are moving at 72 km/h under the full load condition. The DLSF influenced by the different qualities of the road surfaces are shown in Fig. 4(a). The result shows that the DLSF increases quickly when the vehicle moves on the condition of the bad road surfaces of ISO level D and E, and this makes the negative influences on the random road surface, especially with the three-axle heavy truck.

According to Refs. [1, 14], if the DLSF ≤ 1.56, this means that the road-friendliness limit needs to be established. Thus, the condition of the random road surface of ISO level C for the three-axle heavy truck moving and the road surface condition of level D for two-axle and four-axle heavy trucks moving (the value of DLSF < 1.56) is selected as the intervention limit for the random road surfaces. In this circumstance, the traffic management needs to quickly intervene to give a safe velocity limit for heavy trucks when they move on these road surfaces, concurrently, these road surfaces need to be repaired.

Fig. 4Effect of the different operation conditions on the road damage of heavy trucks

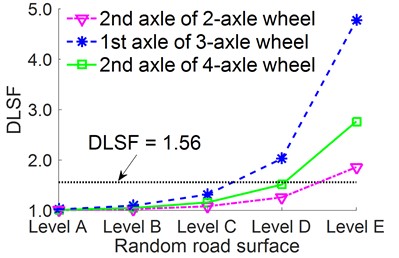
a) Under different road surfaces

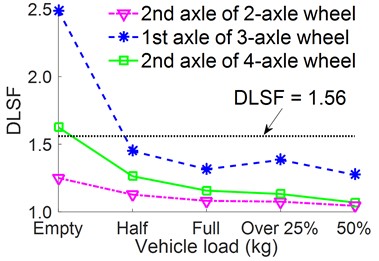
b) Under different loads of vehicle

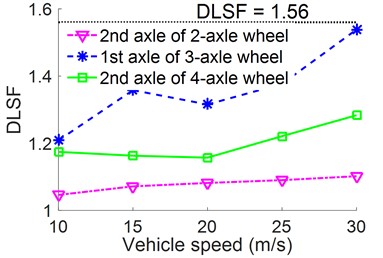
c) Under different speeds of vehicle

4.2. Under the different loads of the vehicle

The vehicle loads not only affect the durability of the vehicle but also affect the random road surface’s fatigue life. In order to analyze the effect of the vehicle loads on the damage of the random road surface, the different load values of heavy trucks as empty load, half load, full load, overload 25 %, and overload 50 % are computed under the same simulation condition in Section 4.1. The simulation result of DLSF with different vehicle loads is plotted in Fig. 4(b). Fig. 4(b) shows that the values of DLSF at axles of heavy trucks increase most quickly when heavy trucks move under the empty load condition and half load condition, especially with the three-axle heavy truck. Thus, it has negatively affected the road surface. When heavy trucks move at overload 25 % and 50 % conditions, the values of DLSF at axles of heavy trucks significantly reduce and it reduces the road damage. However, it has no benefit to the durability of the part of the vehicle and the safe movement of the vehicle. If the vehicle load keeps increasing to some large value, it will no longer affect the DLC and DLSF. Moreover, heavier vehicles will increase the absolute magnitude of dynamic loads, which is the direct cause of road surface damage [15]. Therefore, to reduce the negative effects of this case caused on the road surface, the traffic management needs to quickly intervene to give a safe velocity limit for vehicles when they move on this condition.

4.3. Under the traveling velocities of the vehicle

The vehicle’s moving speed is one of the important causes of the damage of the road surface. To analyze the effect of the vehicle speed on the damage of the road surface, the speed values of heavy trucks including {10, 15, 20, 25, 30} m/s are simulated under the same condition of Section 4.2. The result of the DLSF with different vehicle speeds is plotted in Fig. 4(c). Fig. 4(c) indicates that when the speed of the vehicle is $v \geq$ 20 m/s, the DLSF is quickly increased in the direction of the unfriendly road, especially with the three-axle heavy truck. Therefore, the vehicle’s moving speed need to be limited, especially under the condition of the heavy truck moving on the road surface of ISO level C, D, and E.

5. Conclusions

Based on the research result of the dynamic models of the two-axle vehicle, three-axle vehicle, and foru-axle vehicle, the design parameters of the suspension systems and wheels; and the load distribution of axle-wheels greatly affect the dynamic tire force while the total weight of the vehicle insignificantly affect. Therefore, the systems of the heavy trucks should be desinged to evenly distribute the dynamic load on the wheel axles.

The empty loaded condition of heavy trucks greatly affects the road surface damage, thus, to ensure the safety of the road surface, the traffic management needs to quickly intervene to give the limiting speed for vehicles when the vehicles are traveling as empty loaded condition and the poor road surface condition.

This study not only provides a reference for assessing the influence of heavy trucks on the road-friendliness, but also provides important warning limits for the design of dynamic systems. of heavy trucks to improve safety and reduce road damage.

References

Y. Lu, S. Yang, S. Li, and L. Chen, “Numerical and experimental investigation on stochastic dynamic load of a heavy duty vehicle,” Applied Mathematical Modelling, Vol. 34, No. 10, pp. 2698–2710, Oct. 2010, https://doi.org/10.1016/j.apm.2009.12.006

Publisher
T. Gillespie and S. Karamihas, “Simplified models for truck dynamic response to road inputs,” International Journal Vehicle Design, Vol. 7, No. 1, pp. 52–63, 2000.

Publisher
V. Nguyen, R. Jiao, and J. Zhang, “Control performance of damping and air spring of heavy truck air suspension system with optimal fuzzy control,” SAE International Journal of Vehicle Dynamics, Stability, and NVH, Vol. 4, No. 2, pp. 179–194, Feb. 2020, https://doi.org/10.4271/10-04-02-0013

Publisher
Y. Chen, J. He, M. King, W. Chen, and W. Zhang, “Effect of driving conditions and suspension parameters on dynamic load-sharing of longitudinal-connected air suspensions,” Science China Technological Sciences, Vol. 56, No. 3, pp. 666–676, Mar. 2013, https://doi.org/10.1007/s11431-012-5091-3

Publisher
X. M. Shi and C. S. Cai, “Simulation of dynamic effects of vehicles on pavement using a 3D interaction model,” Journal of Transportation Engineering, Vol. 135, No. 10, pp. 736–744, Oct. 2009, https://doi.org/10.1061/(asce)te.1943-5436.0000045

Publisher
D. J. Cole and D. Cebon, “Truck suspension design to minimize road damage,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 210, No. 2, pp. 95–107, Apr. 1996, https://doi.org/10.1243/pime_proc_1996_210_251_02

Publisher
J. R. Kilner, “Pneumatic tire model for aircraft simulation,” Journal of Aircraft, Vol. 19, No. 10, pp. 851–857, Oct. 1982, https://doi.org/10.2514/3.44786

Publisher
W. Wang, Y. Song, Y. Xue, H. Jin, J. Hou, and M. Zhao, “An optimal vibration control strategy for a vehicle’s active suspension based on improved cultural algorithm,” Applied Soft Computing, Vol. 28, pp. 167–174, Mar. 2015, https://doi.org/10.1016/j.asoc.2014.11.047

Publisher
L. Sun, “Optimum design of “road-friendly” vehicle suspension systems subjected to rough pavement surfaces,” Applied Mathematical Modelling, Vol. 26, No. 5, pp. 635–652, May 2002, https://doi.org/10.1016/s0307-904x(01)00079-8

Publisher
M. Peter, “Active suspension of a heavy-vehicle driven axle,” Journal of Mechanical Engineering, Vol. 53, pp. 342–350, 2022.

Search CrossRef
G. Tsampardoukas, C. W. Stammers, and E. Guglielmino, “Hybrid balance control of a magnetorheological truck suspension,” Journal of Sound and Vibration, Vol. 317, No. 3-5, pp. 514–536, Nov. 2008, https://doi.org/10.1016/j.jsv.2008.03.040

Publisher
Z. Xie, P. K. Wong, J. Zhao, T. Xu, K. I. Wong, and H. C. Wong, “A noise-insensitive semi-active air suspension for heavy-duty vehicles with an integrated fuzzy-wheelbase preview control,” Mathematical Problems in Engineering, Vol. 2013, No. 8, pp. 1–12, 2013, https://doi.org/10.1155/2013/121953

Publisher
J. Máca and M. Valášek, “Vibration control of bridges under moving loads,” Slovak Journal of Civil Engineering, Vol. 3, No. 4, pp. 1–4, 2006.

Search CrossRef
K. Yi and J. K. Hedrick, “Active and semi-active heavy truck suspensions to reduce pavement damage,” SAE International Truck and Bus Meeting and Exposition, Vol. 43, No. 3, pp. 397–384, Nov. 1989, https://doi.org/10.4271/892486

Publisher
“ISO 8068. Mechanical vibration-Road surface profiles-Reporting of measured data,” International Organization for Standardization, 1995.

Search CrossRef
C. Dodds and J. Robson, “The description of road surface roughness,” Journal of Sound and Vibration, Vol. 31, No. 2, pp. 175–183, 1973.

Publisher
D. Cebon, Handbook of Vehicle-Road Interaction. Lisse: Netherlands Swets-Zetinger Press, 1999.

Search CrossRef

About this article

Received

25 October 2022

Accepted

16 December 2022

Published

18 January 2023

DOI

https://doi.org/10.21595/marc.2022.23020

Keywords

heavy trucks

dynamic models

random road surfaces

road surface damage

Acknowledgements

This study is supported by the Key Scientific Research Project of Hubei Polytechnic University (No. 22xjz02A).

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Next article in issue Next

Research article

2023 03 13

Improving ride comfort and road friendliness of heavy truck using semi-active suspension system

Hao Li, Vanliem Nguyen

Research article

2020 12 11

Vibration research of heavy trucks. Part 1: Sensitivity analysis of dynamic parameters on ride comfort

Yongzhu Hu, Vanliem Nguyen, Yong Ye

Research article

2020 12 11

Vibration research of heavy trucks. Part 2: Optimization of vehicle dynamic parameters

Yong Ye, Vanliem Nguyen, Yongzhu Hu

Research article

2019 03 15

Ride comfort performance of heavy truck with three control cases of semi-active isolation systems

Van Liem Nguyen, Van Quynh Le

M. Sun and V. Nguyen, “Vibration influence of different types of heavy-duty trucks on road surface damage,” Maintenance, Reliability and Condition Monitoring, Vol. 3, No. 1, pp. 1–9, Jan. 2023, https://doi.org/10.21595/marc.2022.23020

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/marc.2022.23020
UR  - https://doi.org/10.21595/marc.2022.23020
TI  - Vibration influence of different types of heavy-duty trucks on road surface damage
T2  - Maintenance, Reliability and Condition Monitoring
AU  - Sun, Mingming
AU  - Nguyen, Vanliem
PY  - 2023
DA  - 2023/01/18
PB  - JVE International Ltd.
SP  - 1-9
VL  - 3
IS  - 1
SN  - 2669-2961
ER  - 

Copy Ris

Copied to clipboard!

@article{Sun_2023,
	doi = {10.21595/marc.2022.23020},
	url = {https://doi.org/10.21595/marc.2022.23020},
	year = 2023,
	month = {jan},
	publisher = {{JVE} International Ltd.},
	volume = {3},
	number = {1},
	pages = {1--9},
	author = {Mingming Sun and Vanliem Nguyen},
	title = {Vibration influence of different types of heavy-duty trucks on road surface damage},
	journal = {Maintenance, Reliability and Condition Monitoring}
}

Copy Bibtex

Copied to clipboard!

[1]M. Sun and V. Nguyen, “Vibration influence of different types of heavy-duty trucks on road surface damage,” Maintenance, Reliability and Condition Monitoring, vol. 3, no. 1, pp. 1–9, Jan. 2023, doi: 10.21595/marc.2022.23020.

Copy IEEE

Copied to clipboard!

Sun, Mingming, and Vanliem Nguyen. “Vibration Influence of Different Types of Heavy-Duty Trucks on Road Surface Damage.” Maintenance, Reliability and Condition Monitoring 3, no. 1 (January 18, 2023): 1–9. https://doi.org/10.21595/marc.2022.23020.

Copy Chicago

Copied to clipboard!

Vibration influence of different types of heavy-duty trucks on road surface damage

Abstract

Highlights

1. Introduction

2. Dynamics model of different heavy trucks

2.1. Vehicle’s dynamic model

2.2. Different vibration equations

2.3. Vibration excitation sources

3. The damage index of road

4. Simulation result and evaluation

4.1. Under the different road surfaces

4.2. Under the different loads of the vehicle

4.3. Under the traveling velocities of the vehicle

5. Conclusions

References

About this article

Related Articles