Abstract
The current compression sensing sound source recognition algorithm is mainly based on prior knowledge of exact sparsity. This paper proposes the two stagewise weak orthogonal matching pursuit (TSWOMP) compressed sensing reconstruction algorithm for sound source recognition, which selects atoms and detects the reliability of the selected atoms, and deletes the wrong atoms to obtain the final set of atoms. The results of TSWOMP, stagewise weak orthogonal matching pursuit (SWOMP) and conventional beamforming under different frequencies and different SNR are compared through numerical simulation methods. The results show that TSWOMP can effectively reduce the width of the main lobe, suppressing the influence of the side lobes, and improve the resolution. The recognition accuracy of TSWOMP is significantly higher than that of SWOMP. In addition, it can effectively reduce the algorithm's dependence on sparsity.
Highlights
- The TSWOMP algorithm can break through the Nyquist sampling law, solving the problem of excessive dependence on prior conditions.
- The TSWOMP can effectively reduce the main lobe width and inhibit the influence of side lobe, which significantly improves the resolution.
- The sound pressure recovered of TSWOMP is more equal to the sound pressure of the sound source at the same frequency and SNR.
- The recognition results of TSWOMP are more stable and accurate.
1. Introduction
At present, the main way to sound sources localization at home and abroad is to collect sound signals based on the microphone array. The main methods used include delay-sum [1], deconvolution approach to the mapping of acoustic sources [2], near-field acoustical holography [3], and compressed sensing sound sources localization [4]. The sound source imaging method of compressed sensing technology utilizes the sparsity of the sound source to greatly compress the data by projection to the low-dimensional space, and the original sound source signals can be recovered from fewer signal data by using the compressed sensing reconstruction algorithm, which can effectively improve the accuracy and quality of sound source imaging.
In 2006, Donoho et al. [5] proposed the theory of compressed sensing. In the field of sound source localization, many scholars have introduced compressed sensing technology into sound source recognition [6]. The key to compressed sensing is the reconstruction algorithm, which reconstructs the original signal by solving a convex optimization problem. The existing reconstruction methods mainly fall into four categories: greedy pursuit algorithm [7], convex optimization algorithm [8], Bayesian framework algorithm [9], and non-convex optimization algorithm [10]. The greedy pursuit algorithm has been widely concerned and studied for its high reconstruction efficiency and accuracy. The main idea is to select the atoms the most relevant to the observed data and reconstruct the optimal approximation of the observed data onto iteration.
Based on the above content, this paper proposes a two stagewise weak orthogonal matching pursuit (TSWOMP) compressed sensing reconstruction algorithm applied to sound source recognition. The initial atom candidate set is selected through the segmented weak selection criterion. At the end of each iteration, the reliability of the selected atom is checked, and the previously selected wrong atom is deleted from the current atom set to obtain the final result of the iteration [11]. The TSWOMP algorithm can break through the Nyquist sampling law, solving the problem of excessive dependence on prior conditions, and achieve the purpose of simple algorithm steps, small calculations to improving the accuracy and quality of sound source imaging.
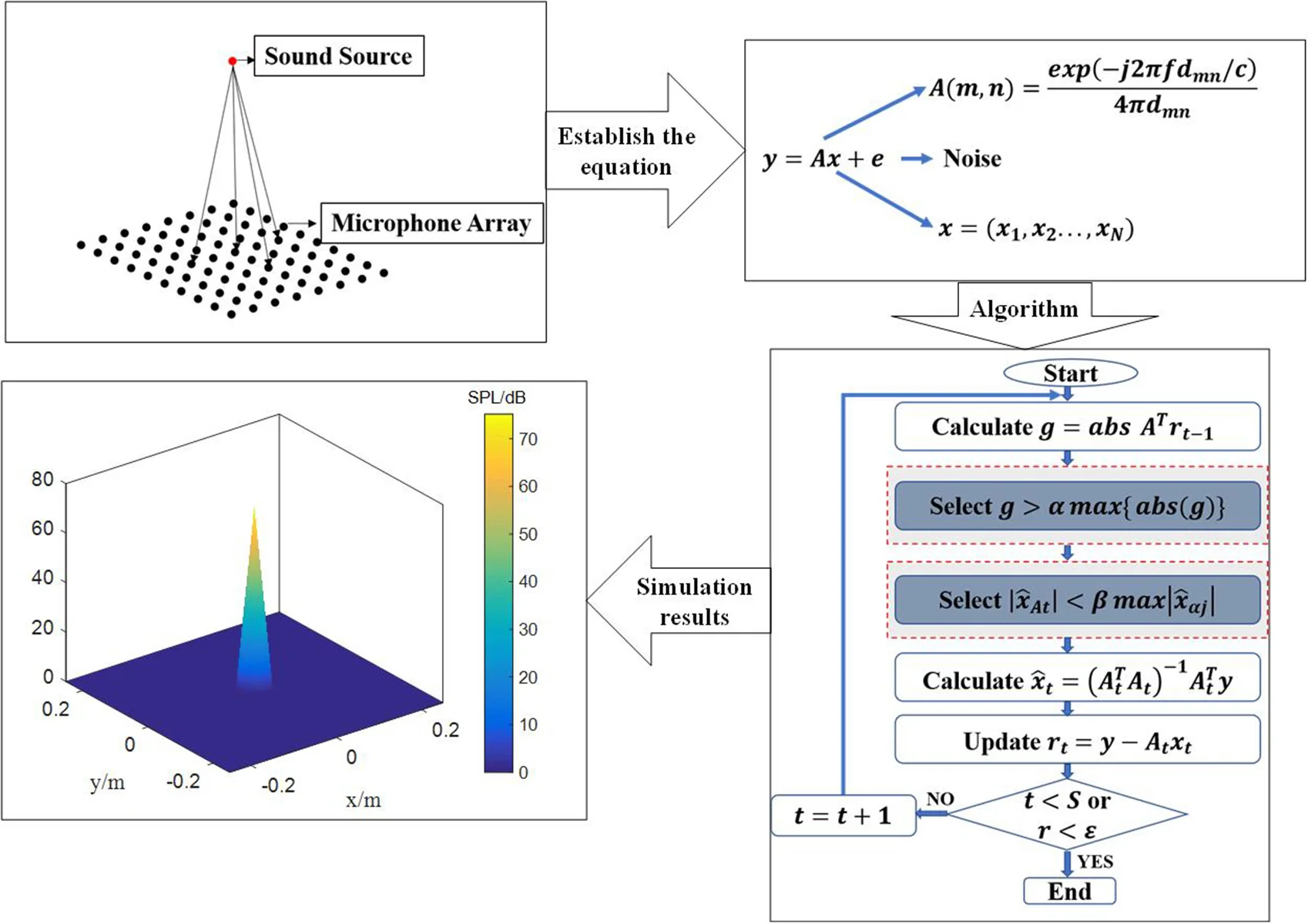
2. Theoretical background of compressed sensing
2.1. The acoustic field model
Assuming that the array is planar, the total number of microphones in the array are , and the frequency of the sound source is , the sound source surface is divided into grid nodes with the same number of row and column nodes, and there are a total of grid nodes. The distance from the m microphone to the n grid node is denoted as (= 1, 2... , = 1, 2... ). According to the Helmholtz integral equation of the free field Green’s function [12], the transfer matrix between the microphone array and the sound source plane node is established, as shown in below Eq. (1):
where is the speed of sound, is the coordinate of the m microphone, is the coordinate of the grid node. Assume that the sound source signal located on the sound source plane can be expressed as , then the microphone measurement value can be expressed as . However, there is some noise in the practical application environment, so the measured value of the microphone is expressed as , where represents noise.
2.2. Reconstruction algorithm
The goal of compressed sensing theory is to reconstruct signal of sparse sound source by measurement value and measurement matrix . The above problem is to solve the underdetermined linear equations, which usually have multiple solutions, owing to . When is a sparse sound source signal, solving can be regarded as the process of seeking the sparsiest solution, which is the process of solving the norm. However, this is a NP-hard problem, which is usually difficult to calculate. In order to solve this problem, Candes and Donoho et al. [13] proposed the idea of replacing norm with norm, so the problem can be expressed as a constraint problem in below Eq. (3), where is determined by the given noise:
Donoho et al. have shown that the solution of norm and the solution of norm are approximately equal under RIP. Greedy tracking algorithm, as a method of compressed sensing reconstruction algorithms, has been widely concerned and researched due to its high reconstruction efficiency and precision. The main algorithms include orthogonal matching pursuit (OMP) [14], stagewise orthogonal matching pursuit (STOMP) [15] and SWOMP [16], where SWOMP has a good performance in terms of complexity and precision. The SWOMP algorithm iterates to the final result by removing the wrong atoms from the set of atoms using a threshold.
3. Reconstruction algorithm of tow weak selection compressed sensing
3.1. Basis of two choices
In the compressed sensing reconstruction algorithm, the SWOMP simplifies OMP and improves the calculation speed. However, the atoms obtained in each iteration are not the best representation of the signal, which leads to a decrease in the reconstruction precision. In practice, the accuracy of the reconstructed signal is far inferior to that of OMP. In addition, the SWOMP can accurately reconstruct the original signal only when the sparsity of the signal is correctly estimated.
To solve the above problems, literature [17, 18] proposed an improved algorithm that relied too heavily on the sparsity, which selected the initial atomic set through the piecewise weak selection criteria, then tested the reliability of the previously selected atoms, and deleted the previously selected wrong atoms from the current atomic set, so as to obtain the final result through iteration. In this paper, the TSWOMP compressed sensing sound source reconstruction algorithm is proposed, which can make the algorithm no longer need the accurate information of sparsity with higher reconstruction accuracy and lower complexity. Ideally, the estimate of the result of the previous step should be greater than the estimate of the result of this step. If, in the process of an iteration, the estimated value of the result obtained according to the first piecewise weak selection criterion is much smaller than the estimated value of the result obtained before, it is very likely that the wrong atom was selected in the previous selection. Therefore, it is necessary to design a "second segmenting weak selection" standard to remove the previously selected wrong atoms from the current atom support set. The second weak selection parameter number is introduced, and the second piecewise weak selection criterion is shown in Eq. (4):
where , is the index of the deleted set of the second weak selection, and is the results obtained before and after the first piecewise weak selection in the -th iteration, respectively.
3.2. TSWOMP algorithm specific steps
According to SWOMP and the above theoretical analysis, the specific steps of TSWOMP are obtained. The sound source signal can be obtained by sensing matrix and measuring signal .
Input: sensor matrix , dimensional observation vector, Number of iterations 10, threshold parameter 0.8 and 0.6.
Output: signal estimation , residual .
Step 1: Initialization , , , .
Step 2: Calculate , select the values in greater than the threshold , and form the set with the corresponding column number of .
Step 3: Make , , if (no new atoms are selected), then the iteration is stopped and step 8 is entered.
Step 4: Find the least squares solution of and , and delete the values that satisfy , the column number of these values corresponding to is , update and .
Step 5: Find the least squares solution of.
Step 6: Update the residual .
Step 7:. If then return to Step 2. If or reaches precision, enter Step 8.
Step 8: The obtained by the reconstruction has a non-zero term at , and the results are obtained by the last iteration respectively, and the rest positions are 0.
3.3. Numerical simulation
In order to verify the feasibility and advantages of the proposed method, the following simulation process adopts CBF, SWOMP and TSWOMP respectively. Based on the simulation results, the influence of frequency and signal-to-noise ratio on sound source localization is analyzed, and the accuracy of sound source identification is analyzed. It is assumed that the sound source is located on the measuring surface, its coordinate is (0, 0, 0), the dynamic range of the sound pressure level is 30 dB, an 8×10 microphone array is adopted, the grid points on the sound source surface are 21×21, the grid spacing is 0.025 m, and the distance from the microphone array to the sound source surface 0.25 m.
After several simulations, TSWOMP can obtain a better reconstruction effect when the weak selection parameters and are 0.5-1, so this simulation takes 0.6 and 0.8. The threshold parameter of SWOMP is set as 0.9. The number of iterations is set as 10.
3.4. The influence of frequency on identification results
The CBF, SWOMP and TSWOMP are used to locate and simulate the sound source at the frequency of 800 Hz and 2500 Hz respectively, and the SNR was 30 dB. The results are shown in Fig. 1 and Fig. 2.
Fig. 1The location results of 800 Hz sound source
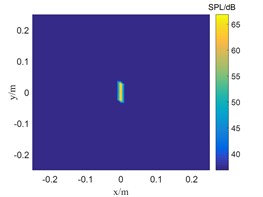
a) TSWOMP
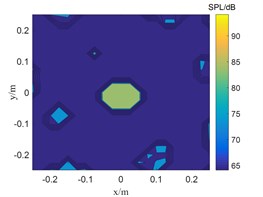
b) SWOMP
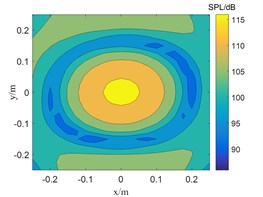
c) CBF
Fig. 2The location results of 2500 Hz sound source
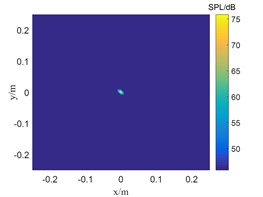
a) TSWOMP
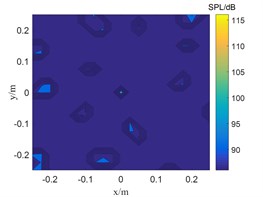
b) SWOMP
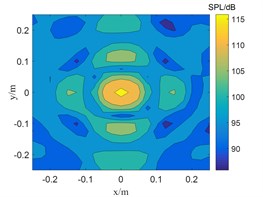
c) CBF
The frequency in Fig. 1 is 800 Hz, and the CBF, SWOMP and TSWOMP can accurately locate the location of the sound source, but there is a large error between the sound pressure values identified by the three algorithms and the sound source pressure values. The main lobe width of CBF and SWOMP are much larger than that of TSWOMP. It can be seen that TSWOMP can effectively reduce the main lobe width, suppressing the influence of side lobe, and significantly improve the resolution at low frequency. The frequency in Fig. 2 is 2500 Hz, and TSWOMP can accurately locate the location and sound pressure of the sound source. The CBF localization results of the main lobe width are much larger than the other two algorithms. Although SWOMP can reduce the width of the main lobe, there are many side lobes and pseudo sound sources, and there is a large error between the recognized sound pressure value and the sound source value. By comparing Fig. 1 and Fig. 2, it is found that with the decrease of frequency, TSWOMP has a certain recognition error in the case of low frequency.
3.5. The influence of SNR on recognition results
A sound source with a frequency of 5000 Hz, the SNR of 15 dB and 0 dB, and a distance of 0.25m from the array to the measuring surface was selected. The CBF, SWOMP and TSWOMP were used for simulation experiments. The results are shown in Fig. 3 and Fig. 4.
Fig. 3The localization results of when sound source the SNR is 15 dB
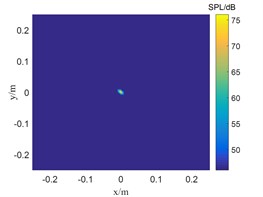
a) TSWOMP
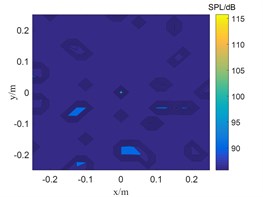
b) SWOMP
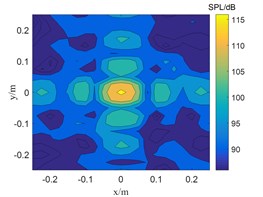
c) CBF
Fig. 4The localization results of when sound source the SNR is 0 dB
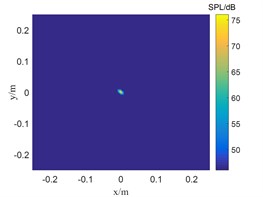
a) TSWOMP
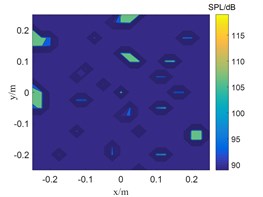
b) SWOMP
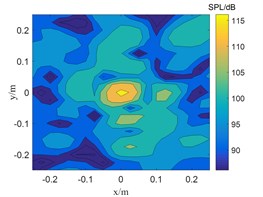
c) CBF
The SNR is 15 dB in Fig. 3, and the sound pressure identified by CBF and SWOMP has a large error with the sound source pressure value, while TSWOMP can accurately identify the sound source location and sound source pressure value. Compared with CBF and SWOMP, TSWOMP has smaller main lobe width, eliminating the influence of side lobe, and reducing the error of sound pressure value reduction. By comparing Fig. 3 and Fig. 4, it can be seen that with the reduction of SNR, CBF and SWOMP are greatly affected by noise, where the main lobe width becomes larger, and the number of side lobes in positioning results increases. However, TSWOMP can effectively reduce the main lobe width, suppressing the influence of side lobes, and improve the accuracy of sound pressure identification of sound source the low SNR.
3.6. Accuracy analysis of identification results
In order to verify the accuracy of TSWOMP recognition results, a frequency of 6500 Hz, a signal to noise ratio of 30 dB, and a distance of 0.25 m from the array to the measuring surface of 100 arbitrary sound sources were taken, then TSWOMP and SWOMP were used for simulation experiments. The results are shown in Fig. 5.
Fig. 5The result of localization any 100 sound sources
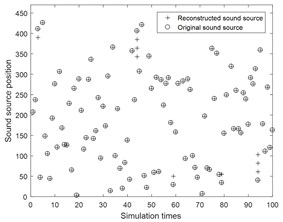
a) TSWOMP
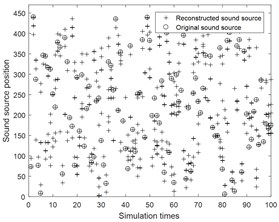
b) SWOMP
Fig. 5 shows that the recognition rate of TSWOMP algorithm is significantly higher than that of SWOMP algorithm. When the grid spacing is 0.025 m, TSWOMP can accurately identify the sound source location. However, the error caused by noise leads to sidelobe in the recognition result. After identifying 2000 random source positions, the sidelobe free probability of TSWOMP algorithm is about 94.8 %.
4. Conclusions
The TSWOMP algorithm can break through the Nyquist sampling law, solving the problem of excessive dependence on prior conditions. Compared with CBF and SWOMP, TSWOMP can effectively reduce the main lobe width and inhibit the influence of side lobe, which significantly improves the resolution, and the sound pressure recovered is more equal to the sound pressure of the sound source at the same frequency. In addition, TSWOMP can also achieve very good results at low SNR. However, TSWOMP has a certain recognition error at the low frequency. Compared with SWOMP, TSWOMP can effectively reduce the dependence on sparsity information, and the recognition results are more stable and accurate. However, the TSWOMP has some errors in the identification results of individual locations of the sound source. Therefore, further research on this problem can be carried out in the follow-up work.
References
-
Tsuneji K. On the main algorithms and system-examples for beamforming: sound source direction estimation by linear array. The Journal of the Acoustical Society of Japan, Vol. 45, Issue 10, 1989, p. 815-822, (in Japanese).
-
Brooks T. F., Humphreys W. M. A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays. Journal of Sound and Vibration, Vol. 294, Issue 4, 2005, p. 856-879.
-
Wu Sean F. Techniques for implementing near-field acoustical holography. Sound and Vibration, Vol. 44, Issue 2, 2010, p. 12-16.
-
Ning F. L., Wei J. G., Qiu L. F., Shi H. B., Li X. F. Three-dimensional acoustic imaging with planar microphone arrays and compressive sensing. Journal of Sound and Vibration, Vol. 380, Issue 13, 2016, p. 112-128.
-
Candès E. J., Romberg J. K., Tao T. Stable signal recovery from incomplete and inaccurate measurements. Communications on Pure and Applied Mathematics, Vol. 59, Issue 8, 2006, p. 1207-1223.
-
Ning F. L., Wei J. G., Liu Y., Shi X. D. Study on Sound Sources Localization Using Compressive Sensing. Journal of Mechanical Engineering, Vol. 52, Issue 19, 2016, p. 42-52.
-
Liu L. F., Fu L. J., Ji F., Xiao X. B., Wu B. Greedy pursuit – an efficient approach from compressed sensing to robust state estimation. IET Generation, Transmission and Distribution, Vol. 12, Issue 9, 2018, p. 2140-2147.
-
Wu S., Tian J., Cui W. A novel parameter estimation algorithm for DSSS signals based on compressed sensing. Chinese Journal of Electronics, Vol. 24, Issue 2, 2015, p. 434-438.
-
Chen G. R. Channel estimation with Bayesian framework based on compressed sensing algorithm in multimedia transmission system. Multimedia Tools and Applications, Vol. 78, Issue 7, 2019, p. 8813-8825.
-
Chartrand Staneva V. Restricted isometry properties and nonconvex compressive sensing. Inverse Problems, Vol. 24, Issue 3, 2010, p. 657-682.
-
Wang B. W., Tan J. Compressed sensing subspace pursuit algorithm based on two stagewise weak selection. Telecommunications Science, Vol. 36, Issue 5, 2020, p. 83-92.
-
Kurkcu H., Reitich F. Stable and efficient evaluation of periodized Green’s functions for the Helmholtz equation at high frequencies. Journal of Computational Physics, Vol. 228, Issue 1, 2009, p. 75-95.
-
Candes E. J., Tao T. Decoding by linear programming. IEEE Transactions on Information Theory, 2005, p. 4203-4215, https://ieeexplore.ieee.org/document/1542412.
-
Zhang Y., Xin G. Y., Zhang X. F. DOA Estimation for uniform linear array with compressive sensing. Applied Mechanics and Materials, Vol. 3744, 2015, p. 1239-1243.
-
Chen Z. H., Lu C., Yuan H. Hydraulic pump fault diagnosis with compressed signals based on stagewise orthogonal matching pursuit. Vibroengineering Procedia, Vol. 5, 2015, p. 223-228.
-
Zhang Y. Y., Sun G. L. Stagewise arithmetic orthogonal matching pursuit. International Journal of Wireless Information Networks, Vol. 25, Issue 2, 2018, p. 221-228.
-
Cen Y., Wang F., Zhao R. Tree-based backtracking orthogonal matching pursuit for sparse signal reconstruction. Journal of Applied Mathematics, Vol. 2013, 2013, p. 864132.
-
Li J., Xu Z. J., Zhang P. Compressing sensing based BAOMP algorithm channel estimation in NC-OFDM system. Microcomputer and its Applications, Vol. 33, Issue 14, 2014, p. 53-56.
About this article
This work was supported by the National Natural Science Foundation of China (Grant No. 61701397 and 51705419) and the Fundamental Research Funds for the Central Universities, CHD (Grant No. 300102210512 and 300102210511).
