Wavelet packet analysis on blasting vibration signal under different cutting method

2.1. Wavelet packet analysis

For the wavelet analysis, the signal is decomposed into two parts, i.e. low frequency part and high frequency part. In the next decomposition, only the low frequency part is decomposed again, and so on until the decomposition is completed. It could be clear that the resolution of low-frequency wave is higher than that of high-frequency wave in the wavelet decomposition, which results in a low resolution of high-frequency part of the wave. However, in the process of wavelet packet, each decomposition round not only the low-frequency part is decomposed in turn, but also the high-frequency part would be decomposed. Therefore, the resolution of the wave in high frequency band has been improved by the wavelet packet analysis method, which is more precise than the traditional wavelet analysis method [19-21].

The data acquisition of blasting vibration adopts TC-4850 blasting vibrometer. The recording time of signal is 2 second, the acquisition frequency is 2KHz, and the Nyquist frequency is 1KHz. The data can be decomposed into 8 layers using the wavelet packet decomposition method. After the first layer decomposition, the data can be divided into two parts: low-frequency S_A0 (0, 500 Hz) and high-frequency S_A1 (500 Hz, 1000 Hz). The second layer is to further decompose the S_A0 and S_A1, and to decompose S_A0 into low-frequency S_B0 (0,250 Hz) and high-frequency S_B1 (250 Hz, 500 Hz), and to decompose S_A1 into low-frequency S_B2 (500 Hz, 750 Hz) and high-frequency S_B3 (750 Hz, 1000 Hz) and so on. When it is decomposed into layer 8, S_H0 (0, 3.906 Hz), S_H1 (3.906 Hz, 7.813 Hz), S_H2 (7.813 Hz, 11.718 Hz) could be obtained up to S_H255 (999.094 Hz, 1000 Hz).

2.2. Principle of energy spectrum analysis

For the blasting vibration signal $S\left(t\right)$, $2^i$ sub-bands could be obtained in the $i$ layer through decomposition. Then $S\left(t\right)$ can be expressed as [22, 23]:

In the formula, the blasting vibration signal is decomposed into the reconstructed signal $f_{i,j}\left(t_j\right)$ on node $\left(i,j\right)$ for the $i$ layer by wavelet packet. If the frequency width of signal $S\left(t\right)$ is $\omega$, the frequency width of each sub-band in $i$ layer is equal to $\omega /2^i$.

For energy $E_{i,j}\left(t_j\right)$, corresponding to signal $f_{i,j}\left(t_j\right)$, it would be:

In which, $x_{j,k}\mathrm{}(j=\mathrm{0,1},2,\cdots ,2^i-1,\mathrm{}k=\mathrm{1,2},\cdots ,m)$ is the amplitude of discrete points $f_{i,j}\left(t_j\right)$, and $m$ is the acquisition number of blasting vibration signal.

From Eq. (2), the total energy $E$ of blasting vibration signal $S\left(t\right)$ is obtained as follows:

When the signal $S\left(t\right)$ is decomposed into $i$ layer, the ratio of the energy of each frequency band to the total energy of the signal could be as follows:

3.1. Principle of cutting way

The emulsion explosive is used for the blasting here. Each volume explosive weight is 0.3 kg. Meantime, each cycle footage has been kept the same as about 2000 mm. A millisecond delay with non-electric detonator is used to detonate. The cutting holes adopt continuous coupling charge, the auxiliary holes and the bottom holes adopt continuous non-coupling charge, the surrounding holes adopt the air interval with non-coupling charge to bind the interval of the explosive to the detonator. The blockage length of the surrounding hole and auxiliary hole is not less than 20 cm, while the cutting hole is not less than 40 cm.

The maximum value of blasting vibration velocity generally appears at the position of maximum tensile stress, while the position of maximum tensile stress of excavation roadway is generally at the top of roadway. Therefore, one of the vibration velocity sensors has been installed at the top of roadway to estimate the distribution of vibration intensity on the roadway excavation section.

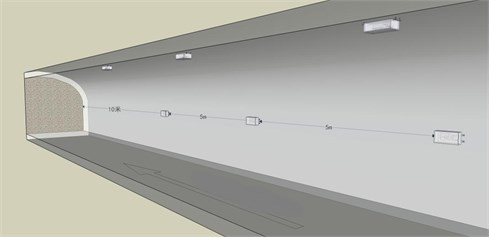
Based on the above analysis, it is considered that the blasting vibration speed at the top of the roadway is the largest. It means that the top vibration resistance of the roadway is the worst. Therefore, there are three blasting vibration velocity sensors are arranged on the top of the roadway, and the sensor is arranged at the side wall of the roadway at the same position. In which, a three direction sensors are placed at each measuring point, corresponding to the radial, vertical, and tangent directions. The base is fixed on the rock surface by lime powder coupling. As it is shown in Fig. 1.

The first measuring sensor point is arranged 10 m away from the blasting face, and the other sensors are arranged at intervals of 5 m. That is, three sets of sensors and six measuring points are linearly arranged along the top and side of the roadway from the blasting face.

According to the blasting design, the cut hole is arranged at the lower position of the center of the working face. The cutting hole is the first to detonate, so the central rock would be throw out, the free face for the surrounding rock could be increased, and the blasting effect would be achieved better. The principle can be summarized as follows, most importantly, a part of rock on the working face should be broken down to make the working face form a second free face, which creates favorable conditions for the blasting of other blast holes [24]. It means that the cutting method is mainly changed while the other blasting parameters remain unchanged. At the same time, the number of boreholes and the total charge of each cutting method are kept as consistent as possible, but the space distribution of the cutting holes is different. Moreover, the distribution area of each cutting in the face is roughly the same. Finally, the number of explosive consumables used in different cutting methods is consistent. Then the testing and its results could be scientifically credible.

Fig. 1Layout diagram of blasting vibration observation point of roadway roof and side wall

The quality of cutting plays a decisive role in improving rock breaking efficiency and blasting cyclic footage. Therefore, it is necessary to select a reasonable cutting method to induce the rock completely broken to form an ideal cavity.

The selection of cutting mode is an important link, and its main purpose is to provide compensation space and free surface for the whole blasting operation. In the case of comprehensive analysis of geological conditions, environmental and equipment factors, the selection of appropriate cutting method could have a direct impact on the blasting effect. According to the different conditions of roadway section, rock properties and geological conditions, there are many kinds of cutting hole arrangement, which can be summarized into three types as follows, straight parallel hole cutting method, inclined hole cutting method and mixed hole cutting method. Here, the straight parallel hole cutting method, single wedge hole cutting method and double wedge hole cutting method have been devised as shown in Fig. 2.

3.2. Test results

The blasting footage is a main parameter for evaluating the blasting effect, as it can reflect the blasting effect intuitively. According to the pre-designed footage, which is 2 meters, the footage is 1.9 meter for the straight parallel hole cutting, and the hole utilization is about 95 %. While for the other two wedge hole cutting, the blasting footage is 1.8 meter and 1.9 meter separately. In other words, all of these cutting method designed have achieved a desirable blasting footage.

Another parameter for assessing the blasting effect is the half hole ratio of the peripheral hole. After these designed blasting test, there is no residual hole and root. Through statistical analysis, the half hole rates of peripheral hole are generally more than 90 %. It is found that the multi-stage wedge cutting can effectively expand the volume of the cutting cavity and enhance the cutting effect, especially when it face to excavate the large section and hard rock tunnel. The divisional design not only reduces the number of holes, but also ensures the excellent blasting effect.

Fig. 2Blasting scheme of different hole cutting methods (Unit: mm)

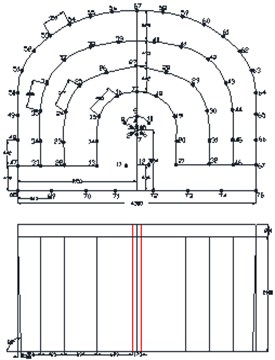
a) Parallel hole cutting scheme

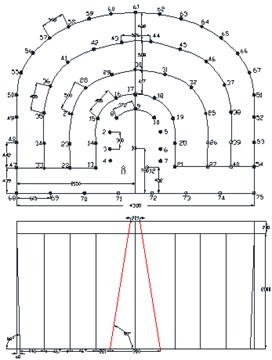
b) Single wedge hole cutting scheme

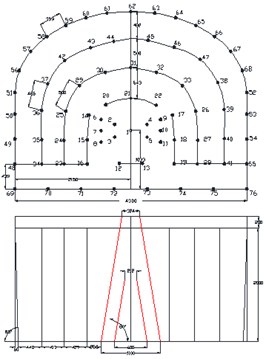
c) Double wedge hole cutting scheme

The third parameter is the rock slag throwing distance and the homogenization degree of rock slag. The adverse effects in drilling and blasting operation are too long or too short throwing distance, high rock block rate and flying rock slag impact. The volume of blasting slag pile mainly comes from the rock in the action area of auxiliary hole. A better forming quality of cutting area could reduce the clamping effect of original rock on auxiliary hole and enhance the throwing force in radial direction. Meanwhile, it could reduce the throwing force of blasting pile in the direction of roadway axis. The rock in the cutting area can be regarded as the main source of flying rock slag. The flying rock slag produced by straight parallel hole cutting is generally less than that produced by inclined hole cutting, and the throwing distance is shorter.

4.1. Blasting vibration velocity analysis

The typical blasting vibration signal waves of these three cutting ways are shown in Fig. 3-Fig. 5.

Fig. 3Typical blasting vibration wave of straight parallel hole cutting

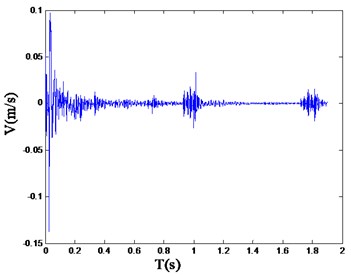
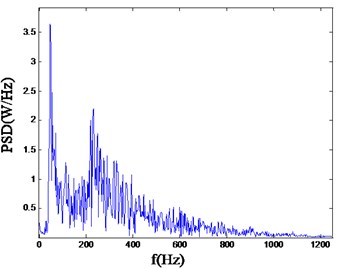
Fig. 4Typical blasting vibration wave of single wedge hole cutting

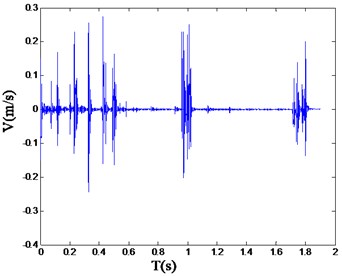
Referring to the safety allowable standard of blasting vibration velocity of various structures in “Blasting Safety Regulations” (GB6722-2015), the reasonable range of the vibration velocity should be limited under 30 cm/s. And the peak values of vibration velocity are 4.4 cm/s, 41.06 cm/s and 16.27 cm/s separately corresponding to the straight parallel hole cutting, single wedge cutting and double wedge cutting. In which, the peak value of the single wedge cutting exceeds the reasonable range [24].

It should be noticed that, for the single wedge hole cutting, the peak blasting vibration velocity has exceeded the specified value of the Regulations mentioned above. However, the blasting progress is still safe and sustainable. It is clearly elaborated that the main frequency is another parameter to assess the blasting vibration effect, along with the peak blasting vibration velocity.

Fig. 5Typical blasting vibration wave of double wedge hole cutting

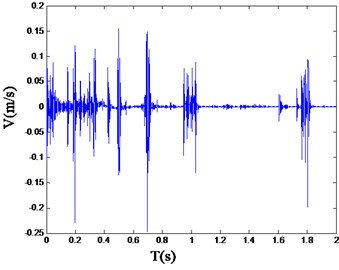
Fig. 6Power spectrum density wave of straight parallel hole cutting

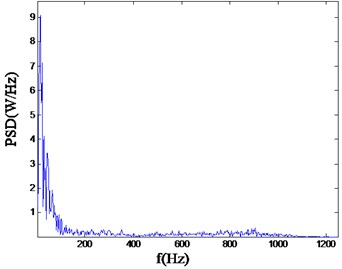
Fig. 7Power spectrum density wave of single wedge hole cutting

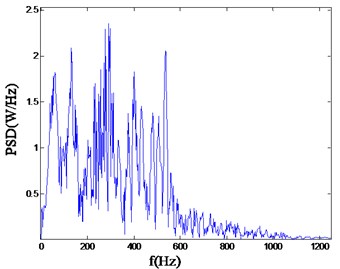
Fig. 8Power spectrum density wave of double wedge hole cutting

4.2. Spectrum analysis on blasting vibration signal

The typical power spectral density curves corresponding vibration waveforms measured with three different cutting modes are shown in the following Fig. 6-Fig. 8.

As can be seen from the above, for straight parallel hole cutting, there is a rather higher ratio in the low frequency band area, mainly concentrated in the range of 0-100 Hz. However, for the single wedge hole cutting, the PSD (power spectrum density) mainly ranges from 0 to 800 Hz. And for the double wedge hole cutting, the PSD mainly concentrated in the higher frequency range, from 0 to 800 Hz. As it is known, the lower main frequency has a more severe adverse effects to the rock and other facilities.

4.3. Blasting energy analysis

Based on the wavelet packet theory, these signals of the cutting methods are decomposed into four layers and the corresponding energy are drawn in Fig. 9-Fig. 11.

Fig. 9Energy distribution of straight parallel hole cutting by wavelet packet decomposition

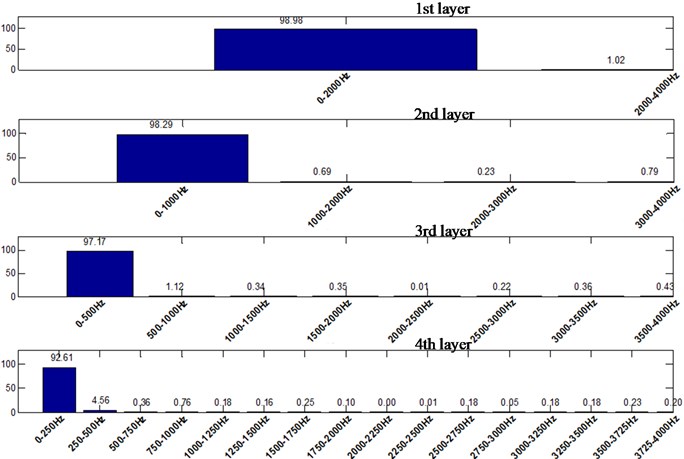
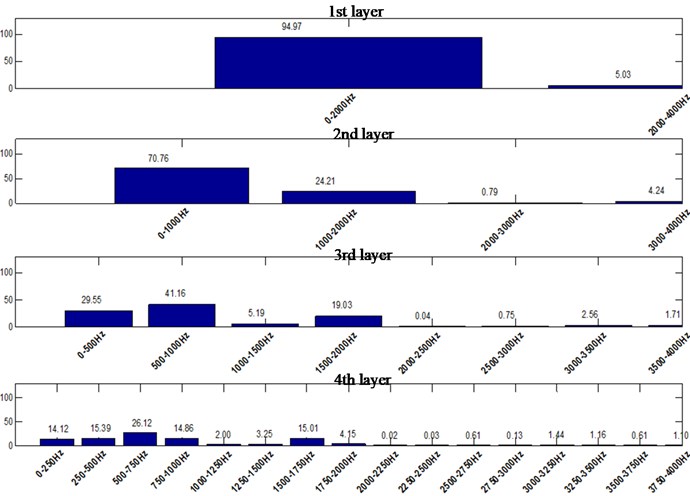
Fig. 10Energy distribution of single wedge hole cutting by wavelet packet decomposition

High frequency part of the signal can be decomposed by wavelet packet, and the decomposition is more detailed. In this way, the characteristics of different frequency components of the original signal could be analyzed by investigating the details of each sub-band, such as the energy distribution of each frequency component and the main frequency band.

Fig. 11Energy distribution of double wedge hole cutting by wavelet packet decomposition

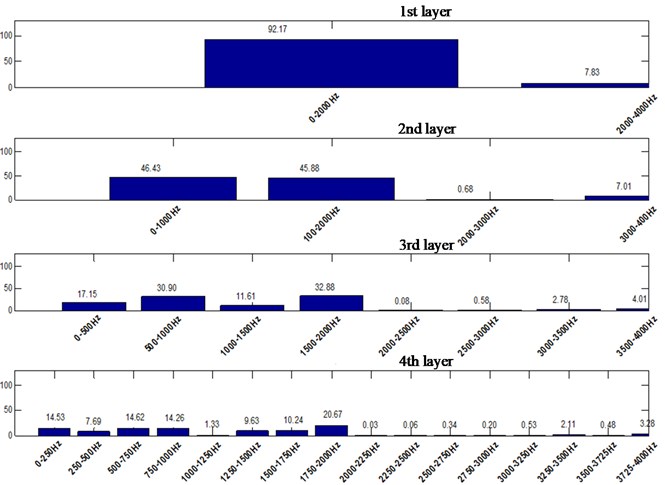
The db3 of Daubechies wavelet series is selected to decompose the signal by the wavelet packet method. Firstly, the layer of wavelet packet decomposition must be determined. The sampling frequency set in this test is 8000 Hz. According to Shannon sampling theorem, the Nyquist frequency is 4000 Hz. Based on the principle of wavelet packet decomposition, the signal can be decomposed into 9 layers, which has 512 (= 2⁹) wavelet packets. Each sub-band has a band width of 7.8125 Hz (= 4000/512 Hz). Then, the corresponding minimum band width is 0-7.8125 Hz, and the maximum band width is 3992.1875-4000 Hz. The energy distribution of blasting vibration signal is shown in Table 1.

It can be seen that for straight parallel hole cutting, the main frequency of blasting vibration is lower, and the energy distribution in the high frequency range is rather narrow. The overall energy distribution is in the low frequency part, and the distribution difference is a bit large.

For the single wedge hole cutting, about 25 % of the energy in the second layer is concentrated in the range of 1000-2000 Hz. In the third layer, about 20 % of the energy is concentrated in the range of 1500-2000 Hz. In advance, for the double wedge hole cutting, the energy distribution is basically uniform, and there is equivalent vibration energy distribution in each frequency band. In the second layer, about 50 % of the energy is concentrated in the high frequency part, that is in the 1000-2000 Hz. Even in the range of 1750-2000 Hz, there is about 20 % of the energy still distributed here.

It is known that the higher the frequency distribution of blasting energy, the more conducive to blasting construction. Therefore, single wedge hole cutting and double wedge hole cutting are more conducive to blasting engineering operation. Especially for double wedge hole cutting, the energy distribution is even in the high frequency part, which should be paid attention to in hard rock engineering.