The influence of sensor installation angle on explosive shock wave overpressure test

2.1. Establishment of finite element simulation model

A finite element simulation model was established based on the actual surface reflected shock wave pressure test site. The 8 kg TNT bare grain was selected for simulation. The length-to-diameter ratio of the grain was 1:1. The detonation method was the central point detonation. The horizontal distance of the projection point is 3 m, 4 m, 5 m, 6 m. Because multiple sensors are placed at the same radius, the sensor installation plate in different positions will interfere with the pressure flow field, which will cause the pressure measured at different measuring points in the same radius. There is a certain error in the value, so only one sensor is arranged at a radius, and the tilt angle of the sensor is 0°, 3°, 5°, 8°, and 10°. The schematic diagram of the installation angle of the sensor installation plate is shown in Fig. 1.

Fig. 1Schematic diagram of installation plate angle

a)

b)

c)

d)

In order to improve the calculation accuracy, the length of the air domain at the measuring points 3 m, 4 m, 5 m, and 6 m is set to 4 m, 5 m, 6 m, 7 m, respectively, with a width of 1 m and a height of 2 m; the width of the concrete area is 1 m, and the height is 0.2 m; The diameter of the installation plate is set to 0.26 m, and the height is 0.1 m. Air is in an ideal gas state, using Euler solver, concrete and sensor mounting plates are solid, using Lagrange solver. At the same time, in order to monitor the change of shock wave pressure, Gaussian monitoring points are placed around the installation plate and at different distances above the concrete. First, establish a symmetrical two-dimensional detonation model to calculate the propagation of the shock wave of the TNT explosive in the two-dimensional model, and then use the Remap technology to map the shock wave to the three-dimensional model to continue the calculation. Fig. 2 shows the established mapped three-dimensional model.

Fig. 2Numerical simulation model: a) The overall diagram of the calculation model before mapping, b) Calculate the simulated overall picture after mapping

a)

b)

2.2. Material state equation and parameters

In the above model, air is an ideal gas, and the density is 0.001225 g/cm³, $E=$ 4.29×10⁶J/kg, JWL state equation is shown in Eq. (1):

where $P$ is pressure, $V$ is volume, $E$ is internal energy, $A$ and $B$ are material parameters, and $R_1$, $R_2$ and $\omega$ are constant parameters.

The material of the sensor mounting plate is STEEL-1006 in the AUTODYN material library, the Liner equation of state is used, and the damage model adopts the Johnson-Cook constitutive model that is suitable for the description of the mechanical behavior of metal materials under impact and explosion loads. The expression is [9-10]:

where: $\sigma$ is the flow stress, $\epsilon$ is the equivalent plastic strain, $A$ is the yield stress parameter, $B$ is the strain strength parameter, $C$ is the empirical strain rate sensitivity coefficient, and n is the hardening index. The main material parameters are shown in Table 1.

3.1. Analysis of the evolution law of shock wave pressure

In order to clearly analyze the evolution law of shock wave in the TNT explosion process, the finite element simulation model of the shock wave pressure evolution cloud map during the explosion process is extracted. Because there are a large number of cloud map moments in the entire simulation process, we select it, and choose the explosion moment at the shock wave evolution cloud diagrams at 2.491 ms, 2.892 ms and 3.392 ms are displayed, as shown in Fig. 3.

From the above-mentioned shock wave pressure evolution cloud diagram, it can be seen that the explosion shock wave spreads in the air in the form of waves. the shock wave does not reflect when it does not meet the ground. Therefore, there is no local high pressure zone. When the shock wave propagates to the ground, reflection occurs. According to the law of shock wave reflection, the reflected pressure is 2-5 times the pressure of the incident shock wave, so a local high pressure area will be formed near the ground, as shown in the red area in Fig. 3.

Fig. 3Cloud diagram of shock wave pressure evolution process

a) 2.491 ms

b) 2.892 ms

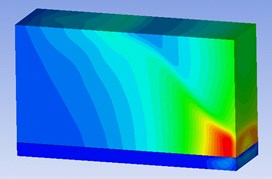
c) 3.392 ms

In order to analyze the impact of the sensor installation plate on the explosion shock wave propagation, the projected point of the explosion center is 3 m and the sensor installation plate inclination angle is 10°. the explosion moments are 2.495 ms, 2.534 ms, 2.589 ms, 2.638 ms, 2.689 ms and 2.728 ms respectively Analyze the evolution cloud diagram of the explosion shock wave at time, as shown in Fig. 4.

Fig. 4Cloud diagram of pressure evolution around the installation plate (tilt angle is 10°)

a) 2.495 ms

b) 2.534 ms

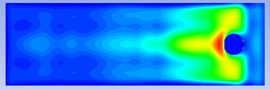
c) 2.589 ms

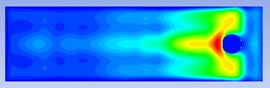
d) 2.638 ms

e) 2.689 ms

f) 2.728 ms

Analyzing the evolution process of the shock wave in Fig. 4, it can be seen that: (1) the evolution of the shock wave of the explosion in the air is a diffusion process that gradually attenuates from near to far in the form of a spherical wave. (2) When the sensor is installed on the plate without an angle, the pressure sphere of the shock wave will attenuate more uniformly in all directions, but when the sensor is installed on the plate at a certain angle, the spread of the shock wave will be hindered by the installation of the plate. the shock wave pressure will accumulate at the front end of the obstacle to form a local high pressure zone. the shock wave pressure here will be higher than the pressure in the surrounding area for a certain moment, but as the explosion time continues, the shock wave pressure will bypass this the obstacle continues to spread far away, and the pressure at the front end of the obstacle gradually drops, attenuating to a situation that is consistent with the surrounding pressure.

3.2. Analysis of simulation results

The above analysis of the evolution process of the shock wave in the air and the influence of the angle of the sensor installation plate during the propagation process of the shock wave, but the specific shock wave overpressure data cannot be directly obtained from the evolution cloud chart of the explosion shock wave, so it cannot be quantified. Analysis, so the overpressure value extraction is performed on the above shock wave simulation results, and the explosion shock wave overpressure time history curve and overpressure peak data at different distances and different angles are obtained. However, because the above shock wave curves are too many to display all of them, so Take the pressure time history curve obtained at a distance of 3 m from the burst center and the inclination angle of the sensor installation plate being 0°, 5°, and 10° respectively as an example for display, as shown in Fig. 5.

The above shock wave overpressure time curve is numerically extracted, and the peak value of shock wave overpressure is obtained at a distance of 3 m, 4 m, 5 m from the center of the burst, and the inclination angle of the sensor installation plate is 0°, 3°, 5°, 8°, 10°, respectively, as shown in the Table 2 and based on the shock wave overpressure peak when the installation angle is absolute zero, calculate the relative error between the overpressure peak at the other angles and the overpressure peak at absolute zero. the calculation results are shown in Table 3.

Fig. 5Pressure waveform diagram at 3m at different inclination angles

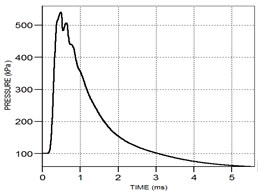
a) The inclination angle is 0°

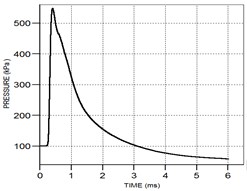
b) The inclination angle is 50

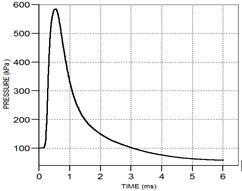
c) The inclination angle is 10°

Analyzing Table 2 and Table 3, it can be seen that the peak pressure of the reflected shock wave on the surface is significantly affected by the inclination angle of the sensor mounting plate. Due to the inclination of the installation plate, when the shock wave propagates to its surface, reflection will occur, causing the shock wave pressure around the plate to increase. When the shock wave encounters the mounting plate with different tilt angles, the incident angle of the shock wave increases with the increase of the tilt angle, so the pressure value measured by the sensor also increases, that is, the larger the tilt angle of the mounting plate, the corresponding Gaussian monitoring the greater the pressure value at the point; with absolute zero as the ideal value, the greater the tilt installation angle of the mounting plate, the greater the impact of the installation angle on the shock wave pressure measurement results. for example, when the inclination angle of the installation plate is 10°, the maximum relative error of the measured shock wave pressure value on the ground surface can reach 17.3 %. Therefore, in order to ensure the accuracy of the measurement results, the installation plate should be as flush with the ground as possible when performing the shock wave pressure test on the surface of the reflection spend.