Altitude influence on the explosion shock wave pressure distribution

1. Introduction

During the process of ammunition explosion, various forms of damage are produced, such as shock waves, high-temperature fireballs, and fragments [1-3]. The explosive shock wave is one of the main parameters of damage and is usually used to evaluate the destructive power of ammunition. Therefore, it is particularly important to accurately obtain the distribution law of shock wave pressure during the process of ammunition explosion. However, it has been found in practical testing that there are significant differences in the distribution of shock wave pressure produced by the same type of ammunition at different altitudes. Due to the inconsistent data obtained, it is not possible to accurately evaluate the destructive power of ammunition or provide a reasonable explanation for related experimental phenomena [4-5]. Therefore, it is necessary to study the effect of altitude on the distribution law of explosive shock wave pressure, clarify the interaction mechanism between them, and provide theoretical guidance and support for the study of the distribution law of explosive shock wave pressure at different altitudes.

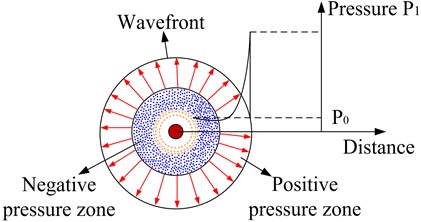
When ammunition explodes, the sharp expansion of the explosive products leads to strong compression of the gas at the interface between the explosive products and the air, which results in the formation of initial shock waves due to the high pressure area in the local region caused by the compression. The process of generating explosion shock wave pressure is shown in Fig. 1 [6-9].

The explosive products have extremely high velocities during the expansion process, which causes excessive compression of the air due to inertial effects, resulting in the pressure at the rear surface of the explosive products being lower than the initial pressure of the air, forming a negative pressure zone. Due to the existence of the negative pressure zone, the high-pressure zone acts back on the negative pressure zone, causing the pressure in the negative pressure zone to gradually increase. Similarly, excessive compression under inertia causes the pressure of the explosive products to be slightly greater than the stable pressure. After experiencing several cycles of shock wave pressure compression pulsation, the explosive products eventually come to a stop and reach an equilibrium state. For air, only the first expansion-compression process has practical significance.

Fig. 1Shock wave pressure formation and distribution

The conversion relationship between explosive products and shock wave pressure during the process of ammunition explosion can be described using the JWL state equation, which is shown in Eq. (1) [10-12]:

where $P$ is the pressure; $V$ is the volume; $E$ is internal energy; $A$ and $B$ are material parameters, $R_1$, $R_2$ and $\omega$ are constants. $A=$3.712×10¹¹, $B=$3.23×10⁹ Pa, $R_1=$ 4.15, $R_2=$ 0.95, $\omega =$ 0.30, initial internal energy $E=$4.29×10⁶ J/kg [13-15].

Based on the above function relationship, it can be seen that under consistent explosive parameters, the peak pressure of the shock wave generated by the explosion is directly related to the atmospheric parameters of the current explosion environment. Specifically, when the initial internal energy E of the air in the explosion environment is larger, the pressure of the shock wave generated by the explosion is also larger, and vice versa. According to the relevant theories in aerodynamics and explosion mechanics, the initial internal energy E of the air is closely related to the air density [9, 16-19]. And air density is directly related to altitude and environmental temperature. The function relationship for calculating air density is shown in Eq. (2):

Currently, in the finite element numerical simulation analysis of shock wave pressure propagation distribution in the explosion field, when considering the influence of altitude on the distribution of shock wave pressure propagation, it is mainly achieved by modifying the initial specific internal energy of air in the ideal gas state equation. The ideal gas state equation is shown in Eq. (3) [20, 21]:

where $P$ is the gas pressure; $\gamma$ is the ideal gas state equation parameter; $\rho$ is the air density; ${\rho }_0$ is the initial gas density; $E$ is the energy density. The parameters are shown in Table 1 [22].

At different altitudes, there are differences in the initial specific internal energy corresponding to the air. The function relationship for calculating the initial specific internal energy is shown in Eq. (4):

where, $E_0$ is the air initial specific internal energy, $E_0=$2.068×10⁵ mJ/mg; $P$ is the atmospheric pressure under the test environment, in kPa; $V$ is the air volume, generally $V=1$; $P_0$ is the air pressure under standard atmospheric pressure, in kPa.

From the above analysis, it can be concluded that the impact of altitude on shock wave pressure can mainly be attributed to the effect of air density on shock wave pressure. Specifically, when air density is lower (altitude is higher), the peak pressure of shock wave at the same explosion condition and at the same measurement point is lower, and the shock wave propagation speed is faster. Therefore, in a vacuum environment, the propagation distance and time of explosive products through solid media have a linear relationship.

2. Research on the explosion shock wave pressure distribution law at different altitudes

At present, researchers at home and abroad for the munitions at different altitudes in the air explosion shock wave pressure propagation distribution law has carried out relevant research, and has achieved certain research results. For example, Izadifard et al. [23] used the blast display dynamics simulation software AUTODYN to establish a finite element numerical simulation model of the blast shock wave pressure distribution law at different altitudes, describing the altitude effect on the shock wave pressure distribution law, and the existing blast shock wave pressure calculation function of the relationship between the correction factors introduction for the correction. Dewey et al [24] carried out a simulated experimental study at altitudes ranging from 0 to 15 km (0 to 50,000 in) and measured the peak and specific impulse of the incident shock wave pressure and verified the Sachs proportionality law validity [25] using the data obtained from the experiment. Veldman et al. [26] conducted actual testing and finite element numerical simulation analysis using C-4 explosives under different initial atmospheric pressure at altitude. The layout scheme set up in the actual experiment process is shown in Fig. 2(a). By analyzing the peak pressure and the time it takes to reach the peak pressure obtained under the initial explosion pressure, it was found that there is no significant corresponding relationship between the explosive shock wave pressure and the initial explosion pressure in a small range. However, as the distance between the measuring point and the explosion center increases, the larger the initial environmental pressure value, the greater the peak pressure of the explosive shock wave. The actual test process to obtain the reflected shock wave pressure peak relative rate of change curve shown in Fig. 2(b).

Fig. 2Test design scheme and test results

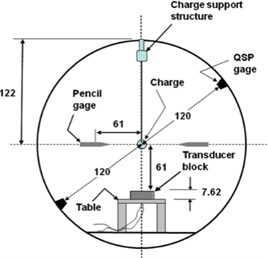
a) Test design scheme diagram

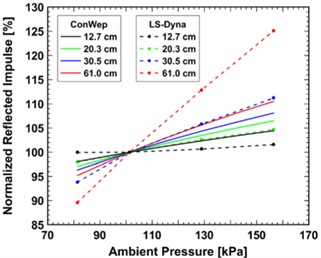
b) Curve of peak relative change rate of reflected pressure

Wang S. Y. et al [27] found that the peak blast shock wave pressure, specific impulse and wavefront surface propagation velocity could not be calculated from the analytical point of view using different air state parameters. Therefore, they chose the nonlinear dynamics simulation software AUTODYN to simulate the distribution law of explosive shock wave pressure under different altitudes. By analyzing the data obtained through simulation, the state equation of air was determined, and a finite element numerical simulation model was established under different altitudes. A comparative analysis of the simulation data and measurement data was conducted to clarify the effect of altitude on the distribution law of explosive shock wave pressure propagation. Gao Y. G. et al [28] found that the difference in altitude would have a significant effect on the explosive slamminess, so they used the air extraction inside the cartridge to simulate the atmospheric environment at altitudes of 500 m, 1500 m, 2500 m, 3500 m and 4500 m, and the cartridge device during the test is shown in Fig. 3(a). The test results show that the altitude change has almost no effect on the expanded explosive slamminess, while for the emulsified explosive, the emulsified explosive slamminess gradually increases with the altitude increase. The slamminess change curve of the two explosives with altitude is shown in Fig. 3(b), (c).

Fig. 3Explosive container device and test results

a) Explosive container device

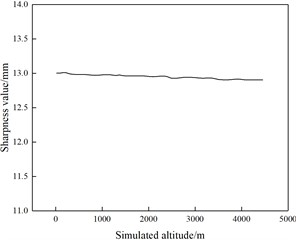
b) Expanded explosive swelling curve

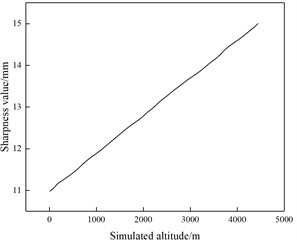
c) Emulsion explosive brisance curve

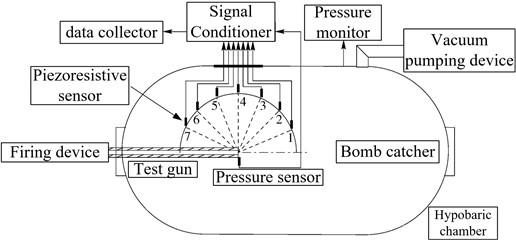
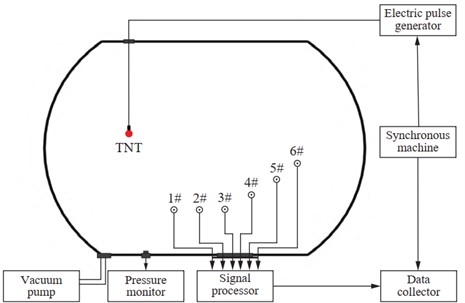
Zhu G. N. et al [29] carried out an experimental study on the shock wave pressure propagation distribution law at the borehole in a low-pressure environment. During the test, in order to simulate the actual low-pressure environment, the low-pressure chamber air pressure was set with the evacuation device, and the shock wave pressure test system was designed as shown in Fig. 4.

Using the testing system, pressure tests were conducted on multiple points outside the muzzle at 7 different altitudes. Analysis of the obtained pressure data revealed that the distribution of shock wave pressure outside the muzzle in low-pressure environments is consistent with that in normal pressure environments, but the peak pressure of the shock wave decreases linearly as the ambient pressure decreases.

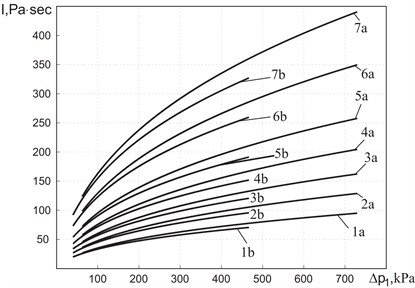
M. V. Silnikov et al. [7, 30] analyzed the role of high-pressure and low-pressure environments on the peak pressure and specific impulse of the blast shock wave. Based on the quantitative similarity criterion principle, a functional relationship between the initial pressure of air and the peak pressure of the blast shock wave was established for the lile calculation. The established functional relationship is shown in Eq. (5). Research results can be applied to the spacecraft explosion safety analysis:

where, $\epsilon =(\gamma -1)/(\gamma +1)$ is the ideal gas shock wave maximum density ratio, and $\gamma$ is the air adiabatic coefficient, usually; $\gamma =\text{1.4}$ is the atmospheric pressure at the standard altitude, and $\mathrm{\Delta }{p}_r$ is the reflected shock wave pressure of the incident shock wave pressure at the rigid interface.

Fig. 4Test device structure diagram

The comparison of the calculation results of the constructed functional relationship with the measured results is shown in Fig. 5. The highly consistent results between the corrected functional relationship formula and the measured results indicate that the calculated function of peak pressure of explosion shock wave established in this study can better reflect the distribution law of explosion shock wave pressure propagation under different environmental pressures.

Fig. 5Comparison between calculated and measured results

Zhao X. L. et al. [31] found that there were significant differences in the explosives detonation velocity when they exploded at different altitudes by analyzing the existing test data. For this phenomenon, they simulated the atmospheric pressure at an altitude of 0 m-4500 m by pumping air from a closed container, and measured the explosives detonation velocity with a detonation velocity meter. The results show that the altitude change will not affect the powder explosives detonation velocity, but for emulsion explosives used in coal mine blasting, the emulsion explosives detonation velocity will first increase and then decrease with the altitude increase. The two explosives detonation velocity variation with altitude during the test is shown in Fig. 6.

Xie X. T. et al. [32] analyzed the explosion shock wave pressure propagation and distribution from the theoretical analysis perspective. The ammunition static explosion shock wave pressure test was carried out at the altitude of 200 m and 4500 m, and the measured test data and the finite element numerical simulation data were compared and analyzed to clarify the plateau effect influence on the explosion shock wave pressure propagation process. At the same time, they also used LS-DYNA and AUTODYN numerical simulation software to carry out research on the ammunition explosion shock wave pressure propagation law at different altitudes, and restored the physical phenomena such as flow around, corner effect and shock wave Mach reflection. The distribution rule of shock wave pressure obtained by simulation is shown in Fig. 7. The research results have important reference significance for the explosion shock wave protection design.

Fig. 6Different explosives detonation velocity variation with altitude

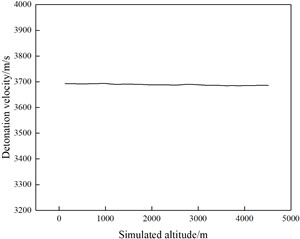
a) Powdered emulsion explosive detonation velocity variation curve

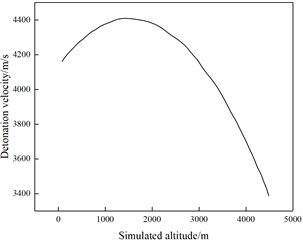
b) Tertiary emulsion explosive detonation velocity curve

Fig. 7Shock wave pressure distribution at different explosion time at 4500 m altitude

a) Explosion time 0.5 ms

b) Explosion time 1.5 ms

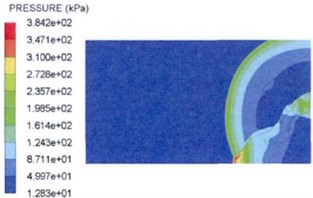
c) Explosion time 2.5 ms

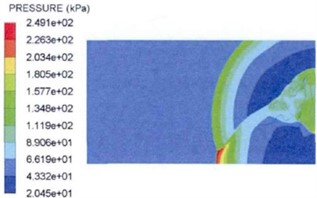
d) Explosion time 3.5 ms

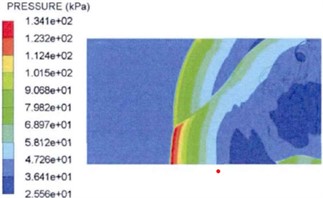
e) Explosion time 6.0 ms

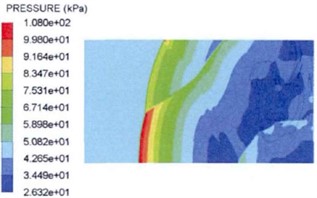
f) Explosion time 8.5 ms

Pang C. Q. et al. [33] based on the Sadovsky formula and the shock wave pressure specific impulse calculation function relationship proposed by Olenko, combined with the shock wave pressure calculation function relationship in unbounded space, constructed the calculation function relationship of peak pressure and specific impulse of explosion shock wave applicable to different altitudes. The constructed calculation function relationship expression is shown in Eq. (6) and (7):

where, $\mathrm{\Delta }{P}_{mGr}$ is the shock wave peak overpressure when the charge explodes on a hard ground, in MPa. $i_{+Gr}$is the shock wave positive relative impulse when the charge explodes on a hard ground, Pa·s; $p_h$ is the atmospheric pressure at the local altitude, MPa; $p_0$ is the atmospheric pressure at sea level, MPa.

To verify the above correction function relationship calculation accuracy, static explosion test research was carried out in the environment with an altitude of 0 m and 4500 m. The comparison between the shock wave pressure data obtained in the actual test process and the calculated value of the established correction function relationship shows that the above correction function relationship is more applicable to engineering than the surface of the results. It provides an effective reference for the further improvement of the warhead plateau shock wave performance index.

Li K. B. et al. [34] found that changes in the environment of explosive detonation directly affect the propagation and distribution process of explosion shock wave pressure. To analyze the impact of environmental characteristics on explosion shock wave pressure, a finite element numerical simulation analysis model of explosion shock wave pressure with different environmental pressures was established. Based on Sacks' proportion law, the characteristic proportional distance is introduced to analyze the influence of near field blast wave pressure characteristic parameters under different environmental pressures, and the functional relationship between the blast wave pressure peak value, specific impulse, positive pressure action time and environmental pressure is established. Ren S. Y. et al. [35] carried out finite element numerical simulation analysis to study the distribution law of the shock wave pressure generated by the mixture explosion of methane and air at different altitudes, and obtained the peak value change law curve of the shock wave pressure generated by the mixture explosion at different altitudes with the altitude, as shown in Fig. 8. It can be seen from the figure that the explosion shock wave pressure peak value decreases gradually with the altitude increase. The research results provide a certain guidance for the methane air mixture explosion protection.

Fig. 8Shock wave pressure variation with altitude

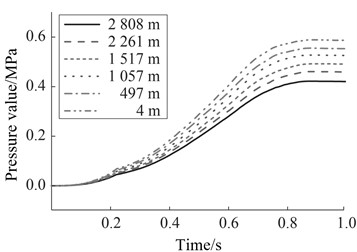
a) Shock wave pressure at different altitudes

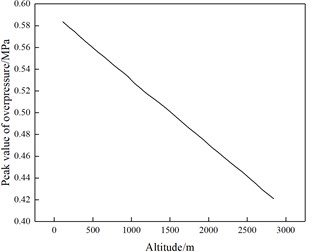
b) Pressure peak value changes with altitude

Deng G. Q. et al. [36] analyzed the ammunition explosion shock wave pressure peak value existing functional relationship, and found that the functional relationship calculation accuracy gradually decreased with the altitude change. Because the Sadovsky formula [37] and HopKinson [38] formula commonly used at present have dimensions, and Sachs formula [39] is a dimensionless correction method. Therefore, on the basis of Sachs formula, using the data obtained in the finite element numerical simulation process, they established the explosion shock wave pressure calculation function relationship, proportional distance and peak arrival time under the altitude correction. The correction function relationship established is shown in Eq. (8):

where subscript $Z$ represents the value at the altitude $Z$, while subscript 0 represents the value at sea level; $\mathrm{\Delta }P$ is overpressure; $\lambda$ is the proportional burst distance; $T_a$ is the arrival time; $I$ is impulse; $S_p$ is the pressure correction factor; $S_d$ is the distance correction factor; $S_t$ is the time correction factor; S_i is the impulse correction factor. These correction factors are calculated as shown in Eq. (9):

where $P_0$ is the atmospheric pressure at sea level; $P_Z$ is the atmospheric pressure at altitude $Z$; $T_0$ is the temperature at sea level (K); $T_Z$ is the temperature (K) at altitude $Z$. According to the standard atmospheric parameters at different altitudes, the shock wave parameters altitude correction factor can be obtained.

To verify the accuracy of the calculation results of the above functional relationship formula, a comparison was made between the numerical calculation results and the calculated results of the modified function model constructed using the Sachs formula, as shown in Fig. 9.

Fig. 9Free field shock wave pressure peak

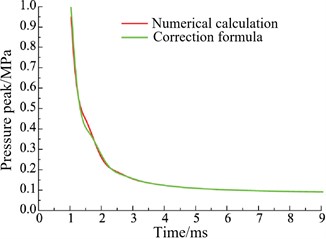
a) Altitude is 2000 m

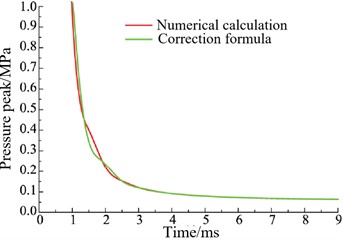
b) Altitude is 5000 m

From the above comparison results of the free-field shock wave pressure, it can be concluded that the functional relationship formula for calculating the peak pressure of explosion shock waves at different altitudes established using the Sachs modification factor can better reflect the effect of altitude on explosion shock wave pressure. The established modified functional relationship formula has strong engineering application value.

Wang Y. et al. [40] used LS-DYNA finite element numerical simulation software to study the shock wave pressure distribution law when the rocket exploded at 0 m-20 km flight height, and obtained the equivalent cloud diagram and the shock wave pressure distribution law during the rocket disintegration at different heights, as shown in Fig. 10.

Fig. 10Rocket aerial explosion finite element numerical simulation results

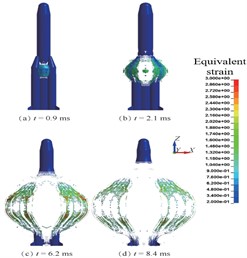
a) Rocket disassembly stress cloud chart in the air

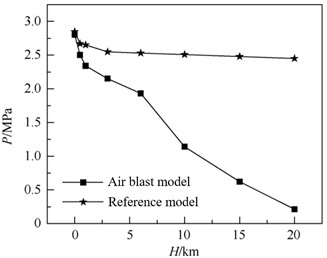
b) Shock wave pressure peak value in rocket air explosion

Based on the results of finite element numerical simulation and the relationship between explosion shock wave and proportional distance, the rocket air explosion shock wave peak pressure calculation function is constructed as shown in Eq. (10). By comparing the shock wave pressure data obtained from the above simulation with the data calculated from the constructed functional relationship, the accuracy of the established functional relationship formula was verified, which has certain engineering application value:

Liu Y. et al. [41] used LS-DYNA finite element numerical simulation software to simulate the atmospheric environment characteristics at different altitudes by changing the air materials relevant parameters, and simulated the kill warheads explosion shock wave pressure field distribution law at different altitudes. By comparing the measured data with the finite element numerical simulation data, the altitude influence mechanism on the attenuation of spherical fragment velocity and the peak attenuation of shock wave pressure is clarified. Using the data obtained from numerical simulation, the existing formula calculation accuracy for calculating the shock wave pressure peak value with altitude correction is verified, and it is proved that the formula has good applicability when the proportional distance is 0.8 m/kg^1/3~1.5 m/kg^1/3. Li Z. M. et al. [42] analyzed the pressure-time curves of reflected blast wave overpressure at different measurement points inside the tank under negative pressure environments of 0, –20, –40, –60, –80, –90, and –99 kPa. It was concluded that the lower the ambient negative pressure, the sparser the gas and the faster the shock wave propagation speed. The blast wave velocity increases as the ambient pressure decreases, and there is no correlation with the decrease in overpressure intensity. In an approximate vacuum environment, the blast wave mainly spreads through the explosion products as the medium, and the increase in shock wave velocity is limited by their movement speed, resulting in low intensity and rapid attenuation. The curves showing the changes in shock wave overpressure and propagation velocity with ambient pressure obtained during the experiment are shown in Fig. 11.

Fig. 11Curve showing the relationship between shock wave parameters and air pressure variation

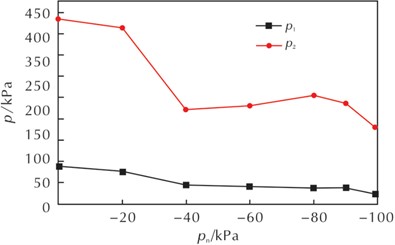
a) Polyline showing the change in shock wave overpressure with ambient negative pressure

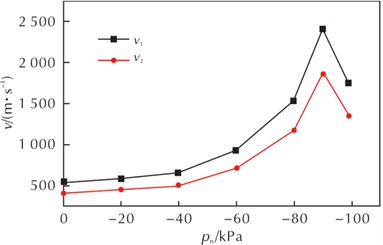
b) Shock wave velocity under different negative pressure environments

Chen L. M. et al. [43] simulated the atmospheric environmental pressure at 500 m, 2500 m and 4500 m above sea level respectively by pumping the explosion tank. The test device structure is shown in Fig. 12.

Fig. 12Test device structure diagram

Based on the above test equipment, the research on the propagation and distribution of TNT explosive static explosion shock wave pressure was carried out, and the influence of different initial gas pressures on the peak pressure and specific impulse of explosion shock wave was obtained, as shown in Fig. 13.

Fig. 13Shock wave pressure characteristic parameters variation law

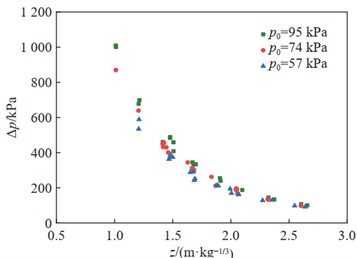
a) Shock wave peak pressure variation law

b) Shock wave pressure specific impulse variation law

Based on Sachs’ proportional law and Sadovsky’s formula, they proposed a correction method under the combined influence of incident shock wave pressure, reflected shock wave pressure, specific impulse and peak arrival time under the influence of atmospheric initial pressure and temperature, and established the calculation function relationship of characterization parameters of explosion shock wave pressure under the altitude influence, this method can significantly improve the explosion shock wave pressure calculation accuracy in a certain altitude range. In 2023 [44], they studied the relationship between ambient air pressure and shock wave parameters, numerically simulated the effects of ambient pressure and temperature on shock wave parameters, and established formulae for calculating the shock wave pressure, specific impulse, and peak arrival time under the influence of air pressure correction. The proposed correction formulae can be applied to parameter calculations within an altitude range of 5000 m.

Lu J. W. et al. [45] developed a small vacuum explosion tank and a large 5 kg TNT explosive masses spherical explosion tank by themselves to study the shock wave pressure propagation characteristics under negative pressure conditions. The two devices are shown in Fig. 14. Experiments on the propagation and distribution of explosion shock wave pressure under different initial ambient pressures were carried out with the two devices developed. Through the acquired shock wave pressure data analysis, the characteristic parameters of the shock wave pressure (peak overpressure, positive pressure action time, specific impulse, shock wave propagation velocity) are preliminarily obtained.

Fig. 14Self developed explosive vacuum tank

a) Small adjustable vacuum explosion tank

b) Spherical vacuum explosion tank

They conducted many tests with the above device, and determined that the peak pressure and specific impulse of explosion shock wave gradually increased with the increase of tank pressure, and the shock wave peak pressure was positively correlated with the initial environmental pressure; The shock wave front propagation velocity decreases with the tank pressure increase, and the two are negatively correlated. The research results provide a theoretical guidance for accurately understanding the propagation and distribution of explosion shock wave pressure caused by altitude.

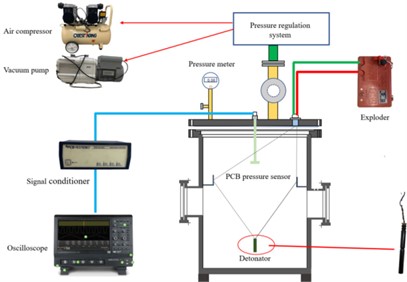
Wang F. Q. et al. [46] developed an explosion vessel with adjustable initial ambient pressure. An explosion shock wave pressure measurement system was built using this vessel. The built shock wave pressure measurement system structural diagram is shown in Fig. 15.

The experimental research on the peak value of explosion shock wave pressure and the ammunition shock wave propagation velocity under different initial environmental pressures has been carried out with the above device. Through the experimental data analysis, it is clear that the explosion shock wave pressure decreases with the initial environmental pressure increase, and the propagation velocity of explosion shock wave increases with the environmental pressure decrease. The test results provide reference data for high-altitude military confrontation, high-altitude weapon design and deep ground protection engineering.

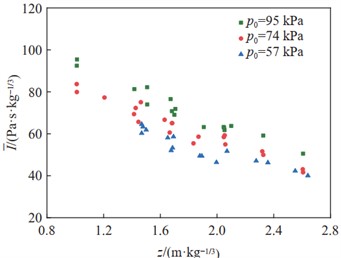
Wang L. Q. et al. [47] analyzed the measured shock wave overpressure data at different altitudes, obtained the altitude attenuation effect on the shock wave pressure propagation process, and proposed a shock wave pressure calculation function relationship considering the altitude influence. The function relationship is shown in Eq. (11):

where, $P_{fix}$ is the shock wave pressure peak value at the determined altitude after correction, $R$ is the measuring point proportional distance, and $P$ is the ambient atmospheric pressure corresponding to the specific altitude.

Fig. 15Explosion shock wave pressure measuring system

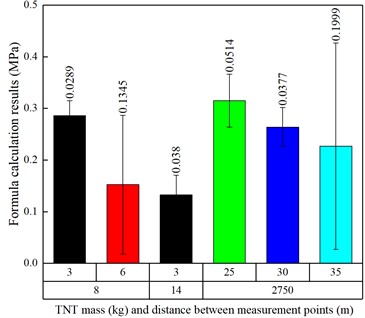
The average error between the shock wave pressure obtained by using the functional relationship formula for shock wave pressure calculation with the introduction of altitude correction conditions and the measured shock wave pressure is 11.1389 %. The verification of the calculated results and the measured results is shown in Fig. 16. As can be seen from the figure, this method can effectively predict the peak pressure of explosion shock waves at different altitudes, providing an effective calculation method for practical engineering testing. The established functional relationship for shock wave pressure calculation is expressed as follows.

Fig. 16Relative error diagram between formula calculation results and measured results

Using dimensional analysis theory and AUTODYN finite element software, Li et al. [48] studied the influence of low temperature, low pressure and altitude on the parameters of explosive blast waves, and established corresponding calculation formulae. The formulae can effectively predict the parameters of explosive blast waves under low temperature and low pressure environments, and clarify that low pressure has a greater effect on the peak overpressure and specific impulse of shock waves than low temperature under high-altitude conditions. The propagation velocity of the blast wave in the near field depends on the pressure, and that in the far field depends on the temperature.

3. Conclusions

Based on the above analysis, it can be seen that the current research on the impact of altitude on the distribution law of explosive shock wave pressure mainly focuses on interpreting experimental phenomena obtained during actual explosion processes through combined use of existing explosion mechanics and aerodynamics theory and finite element numerical simulation analysis results. Then, the effect of altitude is obtained through numerical statistics on the peak pressure of explosive shock wave pressure, time to peak pressure, impulse, and reflected shock wave pressure. There are some problems with the current research status.

1) The existing theoretical basis is not sufficiently applicable. The existing calculation function relationships for peak pressure, impulse, and positive pressure duration of explosive shock waves are all based on the distribution law of shock wave pressure during ammunition explosions in plain environments. When the explosion environment changes, continuing to use these function relationships to calculate the different characterization parameters of explosive shock wave pressure results in unscientific and unreliable results. When revising the existing calculation function relationships, it is not appropriate to simply add a correction factor at the end of the function expression using nonlinear adaptive fitting. The physical meaning of each part of the modified function relationship obtained in this way is unclear, the units of both sides of the function relationship are not unified, and this approach does not have widespread applicability.

2) The analysis of experimental and simulation results is only limited to superficial observations, without in-depth theoretical analysis and explanation. Whether using finite element numerical simulation or obtaining characterization data and experimental observations of ammunition explosion processes from actual testing, it is necessary to theoretically analyze the fundamental causes of such phenomena, clarify the mechanism by which changes in altitude affect the distribution law of shock wave pressure propagation, and fundamentally resolve the mutual influence between the two. Only then can the coupling relationship between altitude and shock wave pressure distribution law be thoroughly understood, and this can truly provide guidance for subsequent research.

Due to the significant impact of altitude on the distribution law of explosive shock wave pressure, studying the effect of altitude on the distribution law of explosive shock wave pressure is of great significance for accurately evaluating the destructive power of ammunition and guiding ammunition design. To study the effect of altitude on the propagation law of explosive shock waves, it is necessary to start from theory, combine with finite element numerical simulation results and carry out actual testing, conduct in-depth analysis of experiment phenomena, and theoretically clarify the relationship and mutual influence mechanism between altitude and shock wave distribution law. Based on existing explosion mechanics theory, a physically clear and reasonably applicable calculation function relationship modification model for shock wave pressure characterization parameters of the explosion field can be established using dimensional analysis methods. The research results can not only improve the theoretical explanation of existing experimental phenomena, but also provide scientific and credible data support and technical guidance for ammunition design and selection.