Motion simulation and impact gap verification of a wheeled vibration-driven robot for pipelines inspection

2.1. General design and simulation model of the wheeled vibro-impact robot developed in the SolidWorks software

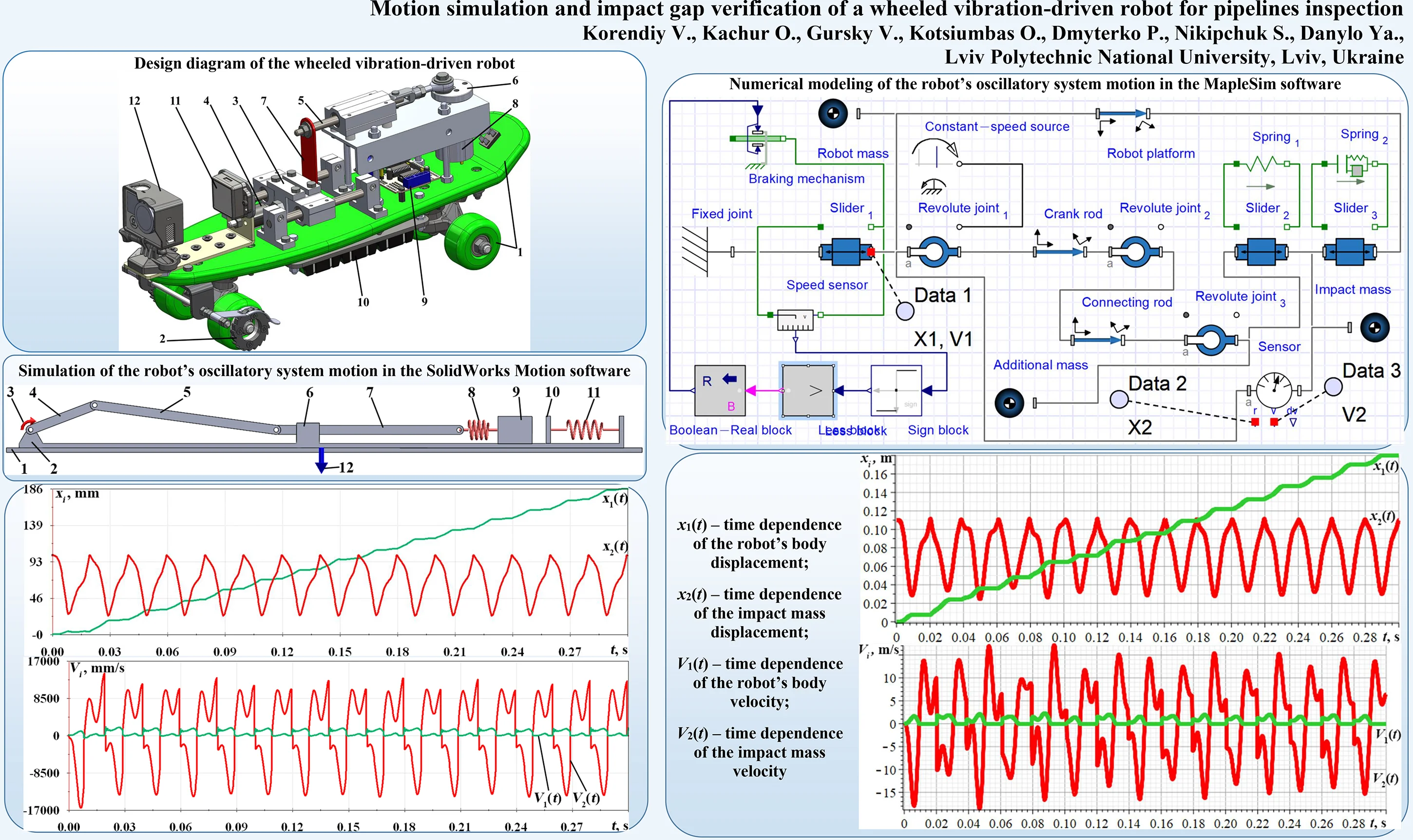
The improved design of the wheeled vibro-impact robot for pipelines inspection was developed in the SolidWorks software (see Fig. 1). The robot is based on the wheeled chassis 1 equipped with the special braking mechanisms 2 allowing only one-way rotation of the wheels. The robot is set into motion due to the sequential impacts of the oscillating body 3 upon the rubber damper 4 fixed to the wheeled chassis 1. The body 3 is connected to the sliding rod 5 of the driving crank (eccentric) mechanism 6 by the flat spring 7. The reciprocating motion of the sliding rod 5 performed due to the crank 6 rotation excites the oscillations of the impact body 3.

Fig. 1Design diagram of the wheeled vibration-driven robot

The crank (eccentric) 6 is driven by the DC motor 8 mounted on the wheeled chassis 1. In order to change the robot motion conditions according to the technological requirements, the machine is equipped with the remote control system 9 powered by the autonomous DC source 10. The robot motion parameters are continuously monitored by the accelerometer 11 sending the corresponding data to the computer for further processing and analysis. The robot’s main function of inspecting the pipelines and monitoring their internal surfaces (welds, couplings, etc.) is provided by the professional video camera 12 fixed on the front end of the wheeled chassis 1.

The simulation model of the robot’s double-mass vibro-impact system is presented in Fig. 2. The robot’s body 2 is placed upon the unmovable rough surface 1 and has the possibility to slide along the horizontal axis. The motor 3 sets the crank 4 into the rotary motion characterized by the constant angular velocity. The crank 4 is hingedly joined with the connecting rod 5 that provides the rectilinear oscillations of the sliding rod 7. The latter moves along the guide 6 fixed on the robot’s body 2. The sliding rod 7 is connected with the impact body 9 with the help of the spring 8. Therefore, the reciprocating motion of the sliding rod 7 provides the rectilinear oscillations of the impact body 9. The translational motion of the robot’s body 2 is characterized by the largest average velocities under the vibro-impact operational conditions. The latter take place due to the sequential impacts of the oscillating body 9 upon the impact plate 10 connected with the movable robot’s body 2 with the help of the spring 11. The interaction between the platform 2 and the rough horizontal surface 1 is simulated by the corresponding friction coefficients and the normal force 12 pressing the platform to the surface. The mentioned force takes its maximal value when the robot’s body 2 attempts to move leftward, while its zero value characterizes the platform state of rest or rightward motion. In such a case, the robot unidirectional sliding is ensured.

Fig. 2Simulation model of the robot’s oscillatory system developed in the SolidWorks Motion software

Fig. 3Simulation model of the robot’s vibro-impact system developed in the MapleSim software

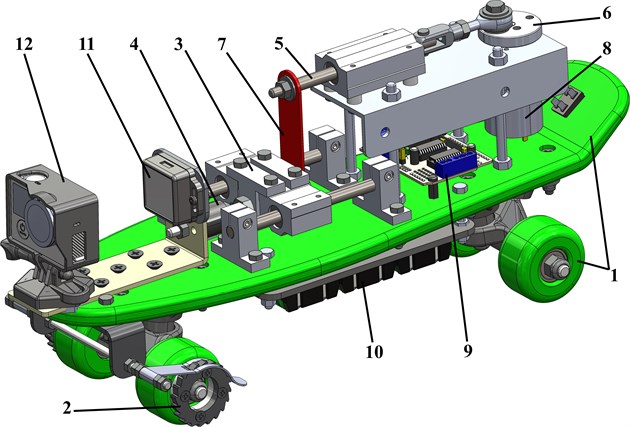
2.2. Simulation model of the robot’s vibro-impact locomotion system developed in the MapleSim software

In order to carry out further numerical modeling of the robot operation, the simulation model of its oscillatory system was developed in the MapleSim software (see Fig. 3). The “Fixed joint” block denotes the initial position of the movable platform, which is simulated by the following blocks: “Slider 1” (wheels), “Robot mass”, “Robot platform” (chassis). The crank-slider excitation mechanism is modelled by the “Revolute joint 1”, “Constant-speed source”, “Crank rod”, “Revolute joint 2”, “Connecting rod”, “Revolute joint 3”, “Slider 2” blocks. The impact body and the impact spring are simulated by the “Impact mass”, “Slider 3”, and “Spring 2” blocks.

In order to restrict the backward motion of the robot’s body, the corresponding “Braking mechanism” block is used. The data obtained from the “Speed sensor” is analyzed by the series of the signal processing blocks “Sign block” (signum function), “Less block” (logical operator), “Boolean-Real block” (signal transformation). In such a case, the control system monitors the robot motion direction and send the signals to the “Braking mechanism” block for restricting the backward motion. The motion simulation results are registered by the following sensors: “Data 1” (absolute displacement and velocity of the robot’s platform), “Data 2” (displacement of the impact mass relative to the crank shaft), and “Data 3” (relative velocity of the impact mass).

3.1. Simulation results obtained in SolidWorks software

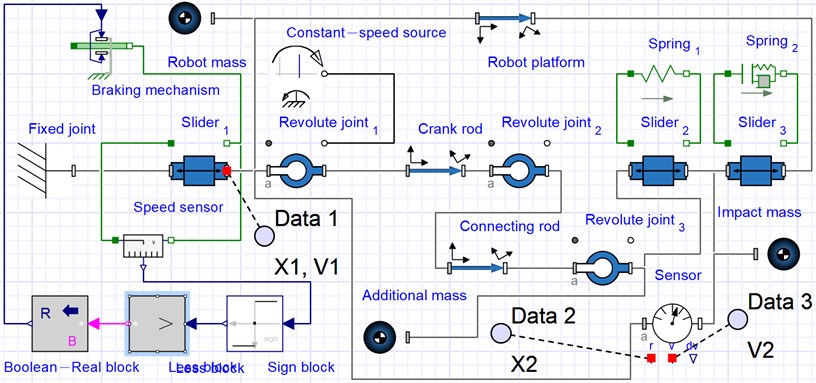
In order to perform further simulation of the robot locomotion in the SolidWorks and MapleSim software, let us introduce the following input parameters: the mass of the wheeled platform $m_1=$ 30 kg; the mass of the impact body $m_2=$ 3 kg; the stiffness coefficients of the corresponding springs (positions 8 and 11 in Fig. 2) $k_1=$ 10⁶ N/m, $k_2=$10⁸ N/m; the lengths of the rods 4, 5, 7 (see Fig. 2) $l_1=$ 0.03 m, $l_2=$ 0.08 m, $l_3=$ 0.08 m; angular speed of the crank rotation $\omega =$ 314 rad/s (the motor shaft rotates at the frequency of 3000 rpm). The initial impact gap, i.e., the smallest distance between the impact mass and the impact plate when the crank excitation mechanism remains at rest, is considered as the controllable parameter influencing the robot’s kinematic and dynamic characteristics. Fig. 4 presents the SolidWorks results of simulating the robot motion conditions when the initial impact gap is equal to zero.

The robot’s wheeled platform displacement reaches about 186 mm during the time period of 0.3 s, while the amplitude value of the impact body displacement is almost 40 mm (see Fig. 4). The maximal speed of the impact body reaches 16 m/s, and the one of the robot body is 1.85 m/s.

Fig. 4Time dependences of the movable platform and impact body a) displacements and b) velocities

a)

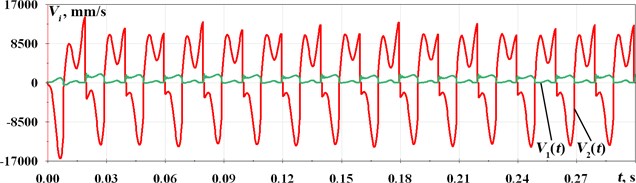
b)

3.2. Results of numerical modeling carried out in MapleSim software

In order to analyze the correctness of the results obtained in the SolidWorks Motion software, let us perform further simulation of the robot motion in the MapleSim software using the corresponding model considered above (see Fig. 3). The input model parameters are the same as those used previously. The obtained results are presented in the form of time dependencies of displacements and velocities of the robot’s movable platform and impact body (see Fig. 5). By the analogy with the results obtained above (see Fig. 4), it can be concluded that the average velocity of the robot’s platform is about 0.6 m/s, while its maximal value reaches 2 m/s; the amplitude values of the impact mass displacements and velocities are about 0.04 m and 16 m/s, respectively.

Fig. 5Time dependences of the movable platform and impact body a) displacements and b) velocities

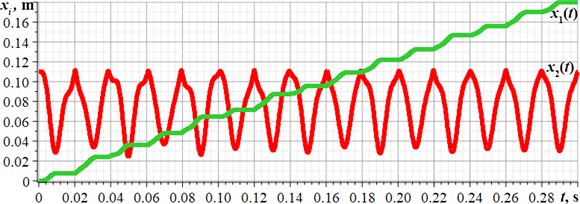
a)

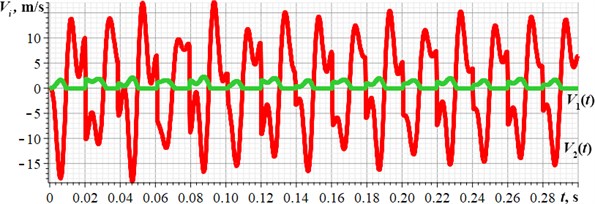
b)

3.3. Studying the impact gap influence on the robot average velocity

In order to analyze the possibilities of maximizing the robot average velocity, let us adopt the impact gap value as the changeable parameter influencing the kinematic and dynamic characteristics of the robot’s vibro-impact system. In our case, the impact gap characterizes the smallest distance between the impact mass and the impact plate when the crank excitation mechanism remains at rest. Previously, the robot’s vibratory system was designed and analyzed under the conditions when the impact gap was equal to zero. Fig. 6 presents the dependencies of the robot’s wheeled platform displacement $x_1$ and average velocity ${\dot{x}}_{1aver.}$ on the impact gap value ranging from 0 m to 0.02 m. The simulation results obtained in the SolidWorks and MapleSim software showed that the maximal value of the wheeled platform average velocity is about 0.7 m/s and takes place in the impact gap range of 0.01…0.012 m.

Fig. 6Dependencies of the robot displacement a) and average velocity b) on the impact gap value

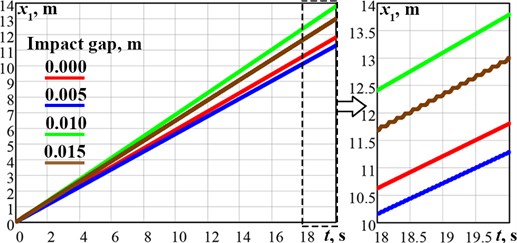
a)

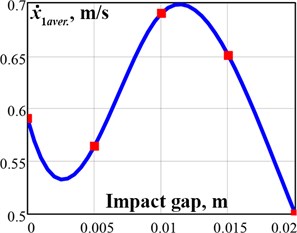
b)