Elastic-plastic solution of circular hydraulic pressure tunnel based on D-P criterion

Ping, Wang

doi:10.21595/vp.2022.22541

Vibroengineering Procedia

Browse Procedia

Published: 16 May 2022

Check for updates

Elastic-plastic solution of circular hydraulic pressure tunnel based on D-P criterion

Wang Ping¹

¹China Railway 16st Bureau Group Road and Bridge Engineering Co Ltd, Beijing, China

Cite the article Download PDF

Downloads 339

Abstract

This work provides new findings on the theory of D–P failure criterion applied to the study of the analytic solution of the radius and stress of tunnel plastic zone and the periphery displacement of hydraulic pressure tunnel under uniform ground stress field. It focuses on elasto-plastic rock masses with the stage of construction and operation. The results that are obtained are compared to other calculation techniques and show that: The elastic-plastic solution calculated based on the theoretical model is larger than that based on the D-P Criterion, indicating safer conditions. The principal stress varies with the internal water pressure, and it firstly decreases to zero and then gradually increase in the plastic zone. With the internal water pressure keeping increasing to a high level, the principal stress in the elastic zone changes from tangential stress to radial stress in the radial distance-enlarging direction, which tends to reach the geostress. In this condition, the radial distance is related to the value of internal water pressure. The calculation results of this study are demonstrated to be in good agreement with those of numerical simulation under the same conditions.

1. Introduction

With the construction of large-scale water conservancy projects such as the Three Gorges Hydropower Station, Jinping Hydropower Station, and the South-to-North Water Diversion Project, a large number of hydraulic tunnels are excavated in China. In these processes, several factors significantly influence the stability and functional use of the tunnels, including the unloading of surrounding rocks, the redistribution of stress, and the emergence of plastic zones. As a result, the stress and the elastic-plastic deformation of hydraulic pressure tunnel have been receiving attention from both the academic and engineering fields.

The studies of axisymmetrical tunnels in perfect elasto-plastic materials and with the Mohr-Coulomb type failure criterion was elaborated by some researchers. When the internal water pressure is extremely high in the hydraulic tunnel, the principal stress changes, producing new plastic zones. In this context, Fenner formula and Kastner formula will be inapplicable. However, there are only a few research achievements about the high-pressure hydraulic tunnel during the operation stage. In the previous theoretical analyses of the elasto-plastic behavior of the rock mass around a circular tunnel [1-8], the circular tunnel is subjected to a hydrostatic in situ stress at infinity, the plane strain assumption are taken into account. For a preliminary design of circular axisymmetric plane strain openings encountered in tunneling problem, an exact and close-form solution with Mohr-Coulomb (M-C) criterion is normally feasible. For the nonlinear yield criteria, the Hoek-Brown criterion [9-11] is also accepted in rock mechanics community, as it provides a reliable tool for predicting the strength of jointed rock mass. However, the D-P failure criterion is widely used in the numerical calculation for the characteristic of no edges and corners. For such cases the D-P failure criterion has been found to be more suitable.

In this paper, the elasto-plastic analysis of rock around a circular pressure tunnel subjected to axial in situ stress and internal water pressure are discussed, using the D-P failure criterion. Effects of the axial in situ stress on the plastic zones, elasto-plastic stresses and periphery displacement around a circular tunnel is analyzed. Influence of the parameters $c$ , $φ$ and $p_{0}$ on the elasto-plastic stresses, and plastic zones around a circular pressure tunnel is also investigated.

2. Elastic-plastic solution of circular tunnels

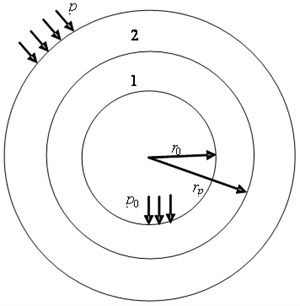
The circular tunnel is assumed in the infinite elastic body, with the tunnel excavation radius of $r_{0}$ , the surrounding rock elastic parameters of $E$ and $υ$ , strength parameters of $c$ and $φ$ , the country rock stress of $p$ , the internal water pressure of $p_{0}$ , and the plastic zone radius of $r_{p}$ (Fig. 1).

The principal stress of the surrounding rock varies with the working conditions. During the construction stage characterized by low internal water pressure, the principal stress is radial stress, while during the operation stage characterized by high internal water pressure, the principal stress is tangential stress. The radial stress as the first principal stress.

Fig. 1Calculation model: 1 – surrounding rock; 2 – country rock

2.1. Stress solutions

The excavation of tunnels is usually associated with the release of geostress, the unloading of surrounding rocks, the redistribution of stress, and the emergence of plastic zones. In axisymmetric case regardless of the body stress, the axisymmetric equilibrium equation under the plane strain condition is:

1

\frac{{d σ}_{r}}{d r} + \frac{σ_{r} - σ_{θ}}{r} = 0 .

D-P yield criterion can be expressed as:

2

f (I_{1}, \sqrt{J_{2}}) = \sqrt{J_{2}} - α I_{1} - k = 0 .

We substitute that and rearrange the balance equation, getting Eq. (3):

3

σ_{r} = C_{1} r^{\frac{6 α}{1 - 3 α}} - \frac{k}{3 α},

where $C_{1}$ is the integral constant, determined by the boundary conditions:

4

C_{1} = (p_{0} + \frac{k}{3 α}) r_{0}^{- \frac{6 α}{1 - 3 α}} .

When we substitute the $σ_{θ}^{e}$ and $σ_{θ}^{p}$ , we can get:

5

\frac{r_{p}}{r_{0}} = {[\frac{(\frac{k}{3 α} + p) (1 - 3 α)}{p_{0} + \frac{k}{3 α}}]}^{1 - 3 α / 6 α} .

Eq. (5) is the expression of the plastic zone radius in the construction stage when the first principal stress is radial. The plastic zone radius changes with geostress, internal water pressure (or supporting pressure), strength parameters and excavation radius.

2.2. Deformation calculation

In the condition that the deformation is small, considering the planar deformation and the material incompressibility:

6

u = \frac{K_{1}}{r},

where $K_{1}$ is the integration constant. Therefore, we can get:

7

ε_{θ} = - ε_{r} = \frac{K_{1}}{r^{2}} .

Considering the general Hooke law, $r_{p}$ can be calculated according to Eq. (8), we can get:

8

u = \frac{r_{p}^{2}}{2 G r} [- (p_{0} + \frac{k}{3 α}) {(\frac{r_{p}}{r_{0}})}^{\frac{6 α}{1 - 3 α}} + \frac{k}{3 α} + p] .

Eq. (8) is the displacement expression.

2.3. The tangential stress as the first principle stress

2.3.1. Stress solutions

In the tunnel operation stage, the tunnel wall can withstand certain internal water pressure. Assuming the internal water pressure is unevenly distributed and disregarding the water weight, the operation condition is still axisymmetric, which means the balance Eq. (1) still apply. If we substitute $σ_{z}$ into the yield equation, we can get:

9

\sqrt{J_{2}} = \frac{σ_{r} - σ_{θ}}{2} .

When $r = r_{p}$ , stresses are continuous, we obtain:

10

\frac{r_{p}}{r_{0}} = {[\frac{(\frac{k}{3 α} + p) (1 + 3 α)}{p_{0} + \frac{k}{3 α}}]}^{- 1 + 3 α / 6 α} .

Eq. (10) expresses the plastic zone radius during the construction stage when the first principal stress is tangential. The radius varies with relevant parameters including geostress, internal water pressure (support pressure), intensity, and excavation radius.

2.3.2. Deformation calculation

Similarly:

11

ε_{θ} = - ε_{r} = \frac{K_{2}}{r^{2}} .

$r_{p}$ can be calculated according to Eq. (10), we can get:

12

u = \frac{r_{p}^{2}}{2 G r} [- (p_{0} + \frac{k}{3 α}) {(\frac{r_{0}}{r})}^{\frac{6 α}{1 + 3 α}} + \frac{k}{3 α} + p] .

Eq. (12) is the displacement expression.

To sum up, during the construction stage, the first principal stress is radial stress, and the plastic zone radius should be calculated according to Eq. (5); during the operation stage, the first principal stress is tangential stress, and the plastic zone radius should be modified according to Eq. (12).

3. Model validation and example analysis

3.1. Model validation

In order to verify the correctness of the model, two different methods respectively based on the D-P criteria and M-C criteria are implemented to calculate the plastic zone radius and stress, with the model parameter $r_{0} =$ 3 m, normal stress $p =$ 15 MPa, high geostress $p =$ 30 MPa, internal friction angle $φ =$ 25°, and cohesion force $c =$ 6 MPa. The plastic zone radius based on the D-P criteria and M-C criteria under the normal stress ( $p =$ 15 MPa, $p_{0} =$ 0) are 3.575 m and 3.495 m, respectively, while those under the high geostress ( $p =$ 30 MPa, $p_{0} =$ 0) are 4.870 m and 4.690 m, respectively.

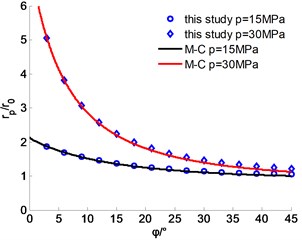
The variation of elastic zone radius with strength parameters is shown in Figs. 2 and 3. Generally, the two methods agree with each other well. When the cohesion force equals or is smaller than 1.2 MPa, the elastic zone radius quickly increases with the decrease of $c$ , which can provide significance guidance for the engineering construction. When the cohesion force is larger than 1.2 MPa, the influence of $r_{p}$ on $c$ is small. Under the high geostress ( $p =$ 30 MPa), friction angle dramatically influences the plastic zone radius (Fig. 3).

Fig. 2The variation of rp with c

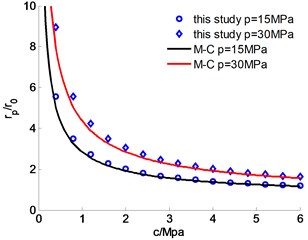
Fig. 3The variation of rp with φ

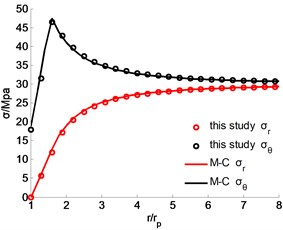
The stress distribution of surrounding rocks under different geostress are shown in Figs. 4 and 5. The tangential stress reaches the maximum in the junction part of plastic and elastic zones. Moreover, the radial stress increases with the geostress, changing from 0 to the geostress gradually. It is identified by both the two methods that tangential and radial stresses are close to the country rock stress at the location the radius is ${8 r}_{0}$ .

Fig. 4Stress distribution under 15 MPa

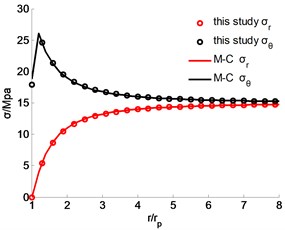
Fig. 5Stress distribution under 30 MPa

3.2. Example analysis

According to the critical condition $r / r_{p} \geq 1$ , the plastic zone radius during the construction stage, previously expressed as Eq. (5), can be rewritten as:

13

p_{0} \leq (\frac{k}{3 α} + p) (1 - 3 α) - \frac{k}{3 α} .

If we substitute the known strength parameters into Eq. (13), we can obtain that $p_{0} \leq$ 3.5585 MPa. It means when $p_{0} \leq$ 3.5585 MPa, there emerges plastic zones in the surrounding rocks, and the plastic zone radius varies with the water pressure. When $p_{0} >$ 3.5585 MPa, there are no plastic zones in the sounding rocks. Similarly, the critical value calculated based on the M-C criterion is that $p_{0} \leq$ 3.2229 MPa, slightly smaller than the result of this study.

During the operation stage, the water pressure is extremely high, contributing to the yield of surrounding rocks again. The plastic zone radius increases with the water pressure, which is expressed as Eq. (14). Given the critical condition that $r / r_{p} \geq 1$ , we can obtain:

14

p_{0} \geq (\frac{k}{3 α} + p) (1 + 3 α) - \frac{k}{3 α} .

If we substitute the known strength parameters into Eq. (14), we can obtain that $p_{0} \geq$ 26.441 MPa. It means when $p_{0} \geq$ 26.441 MPa, there emerges plastic zones again in the surrounding rocks, and the plastic zone radius varies with the water pressure. When $p_{0} <$ 26.441 MPa, there are no plastic zones in the sounding rocks (shown in Fig. 6).

Fig. 6The relationship between the plastic zone radius and internal water pressure

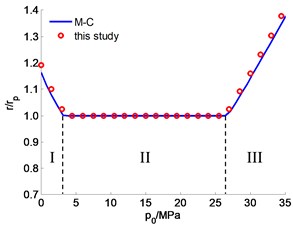
In conclusion, the variation of stresses of surrounding rocks with internal water pressure can be divided into three stages. The first stage (I) is the low water pressure stage ( $0 \leq p_{0} <$ 3.5585 MPa), also referred as the construction stage. The second stage (II) is the medium water pressure stage (3.5585 MPa $\leq p_{0} <$ 26.441 MPa), during which there exists no plastic zone, and the stress distribution can be calculated with the elastic Rummy solutions. The final stage (II) is the high-water pressure stage ( $p_{0} \geq$ 26.441 MPa), during which the plastic zone area increases with the internal water pressure.

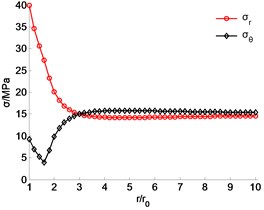
Under the normal stress, the stress distribution during the high-water pressure stage is further analyzed. Figs. 7 and 8 show the stress distribution with the internal water pressure of 30 MPa and 40 MPa, respectively, with corresponding plastic radius of 3.4875 m and 4.9911 m. Moreover, when the tangential or the radial stress is 15 MPa (geostress), the critical radius corresponding to the two different internal water pressure are 6.2863 m and 9.0120 m, respectively. When the radius is larger than the critical value, the first principal stress is tangential again.

Fig. 7Stress distribution with p0 30 MPa

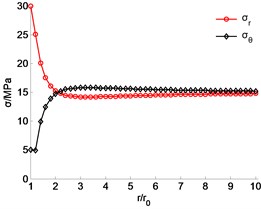
Fig. 8Stress distribution with p0 40 MPa

4. Conclusions

Based on the D-P yield criterion, the elastic-plastic analytical solutions of pressure circular tunnels are derived under the plane strain condition considering different working conditions. Finite element models are established under the same condition, which help reach the following conclusions.

1) Elastic-plastic analytical solutions of pressure circular tunnels during the construction stage are verified to be accurate by comparison with results based on M-C criterion. When $c \leq$ 1.2 MPa, the plastic zone radius dramatically increases with the decrease of cohesion force. However, when $c >$ 1.2 MPa, the plastic zone radius gradually decreases with the increase of cohesion force. Under the high geostress ( $p =$ 30 MPa), friction angle significantly influences the development of the plastic zone. Generally, the plastic zone radius by the model is larger than that based on the M-C criterion, which indicates safer condition.

2) The plastic zone radius decreases with the water pressure when $p_{0} \leq$ 3.5585 MPa. Then the elastic zone disappears when 3.5585 MPa $< p_{0} <$ 26.441 MPa. Again, there emerges the plastic zone when $p_{0} \geq$ 26.441 MPa, with the radius increasing with the water pressure. During the high-water pressure stage, the principle stress of the elastic rock body changes from tangential to radial stress when $r \geq r_{p}$ , and approaches to the geostress. Meanwhile, the radial distance $r$ is related to the internal water pressure.

References

Y. Wang, “Ground response of circular tunnel in poorly consolidated rock,” Journal of Geotechnical Engineering, Vol. 122, No. 9, pp. 703–708, Sep. 1996, https://doi.org/10.1061/(asce)0733-9410(1996)122:9(703)

Publisher
H. Wu, Q. Fang, and Z.-K. Guo, “Zonal disintegration phenomenon in rock mass surrounding deep tunnels,” Journal of China University of Mining and Technology, Vol. 18, No. 2, pp. 187–193, Jun. 2008, https://doi.org/10.1016/s1006-1266(08)60040-1

Publisher
G. Hou and X. Niu, “Perfect elastoplastic solution of axisymmetric circular openings in rock mass based on Levy-Mises constitutive relation and D-P yield criterion,” (in Chinese), Rock and Soil Mechanics, Vol. 30, No. 6, pp. 1555–1562, 2009, https://doi.org/10.16285/j.rsm.2009.06.003

Publisher
Detournay E. and Fairhurst C., “Two-dimensional elastoplastic analysis of a long, cylindrical cavity under non-hydrostatic loading,” International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, Vol. 25, No. 1, pp. A46–A47, Feb. 1988, https://doi.org/10.1016/0148-9062(88)93094-x

Publisher
X. Chen and Cp Tan, “Haberfield CM. Solutions for the deformations and stability of elastoplastic hollow cylinderssubjected to boundary pressures,” International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 23, No. 8, pp. 779–800, 1999, https://doi.org/10.1002/(sici)1096-9853(199907)23:8

Publisher
A. I. Sofianos, “Tunnelling Mohr-Coulomb strength parameters for rock masses satisfying the generalized Hoek-Brown criterion,” International Journal of Rock Mechanics and Mining Sciences, Vol. 40, No. 3, pp. 435–440, Apr. 2003, https://doi.org/10.1016/s1365-1609(03)00017-0

Publisher
A.-Z. Lu, G.-S. Xu, F. Sun, and W.-Q. Sun, “Elasto-plastic analysis of a circular tunnel including the effect of the axial in situ stress,” International Journal of Rock Mechanics and Mining Sciences, Vol. 47, No. 1, pp. 50–59, Jan. 2010, https://doi.org/10.1016/j.ijrmms.2009.07.003

Publisher
J. F. Labuz and A. Zang, “Mohr-Coulomb Failure Criterion,” Rock Mechanics and Rock Engineering, Vol. 45, No. 6, pp. 975–979, Nov. 2012, https://doi.org/10.1007/s00603-012-0281-7

Publisher
X. P. Zhou and J. L. Li, “Hoek-Brown criterion applied to circular tunnel using elastoplasticity and in situ axial stress,” Theoretical and Applied Fracture Mechanics, Vol. 56, No. 2, pp. 95–103, Oct. 2011, https://doi.org/10.1016/j.tafmec.2011.10.005

Publisher
S. K. Sharan, “Elastic-brittle-plastic analysis of circular openings in Hoek-Brown media,” International Journal of Rock Mechanics and Mining Sciences, Vol. 40, No. 6, pp. 817–824, Sep. 2003, https://doi.org/10.1016/s1365-1609(03)00040-6

Publisher
S. K. Sharan, “Exact and approximate solutions for displacements around circular openings in elastic-brittle-plastic Hoek-Brown rock,” International Journal of Rock Mechanics and Mining Sciences, Vol. 42, No. 4, pp. 542–549, Jun. 2005, https://doi.org/10.1016/j.ijrmms.2005.03.019

Publisher

About this article

Received

30 March 2022

Accepted

26 April 2022

Published

16 May 2022

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2022.22541

Keywords

hydraulic tunnel

D-P criterion

elastic-plastic solution

the first principal stress

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2023 04 09

Dynamic damage and response characteristics of the tunnel by FEM modeling and field trials

Xianjun Zheng, Tingyao Wu, Chao Wu, Xiaoqin Wang

Research article

2022 11 03

Influence of multiple random variables on the safety of cracked tunnels under earthquake action

Dongmei You, Feng Gao, Hangchen Lin, Hangling Chen

Research article

2019 11 28

Comparative study for material effect on stress behaviourial characteristics of rectangular plate

Pavan Kishore Mamaduri, Himam Saheb Shaik, Chandrashekhar A

Research article

2019 06 30

Study on distribution law and influencing factors of surrounding rock plastic zone in mining roadway

Chao Yuan, Weijun Wang, Lei Fan

W. Ping, “Elastic-plastic solution of circular hydraulic pressure tunnel based on D-P criterion,” Vibroengineering PROCEDIA, Vol. 42, pp. 125–131, May 2022, https://doi.org/10.21595/vp.2022.22541

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22541
UR  - https://doi.org/10.21595/vp.2022.22541
TI  - Elastic-plastic solution of circular hydraulic pressure tunnel based on D-P criterion
T2  - Vibroengineering PROCEDIA
AU  - Ping, Wang
PY  - 2022
DA  - 2022/05/16
PB  - JVE International Ltd.
SP  - 125-131
VL  - 42
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Ping_2022,
	doi = {10.21595/vp.2022.22541},
	url = {https://doi.org/10.21595/vp.2022.22541},
	year = 2022,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {42},
	pages = {125--131},
	author = {Wang Ping},
	title = {Elastic-plastic solution of circular hydraulic pressure tunnel based on D-P criterion},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]W. Ping, “Elastic-plastic solution of circular hydraulic pressure tunnel based on D-P criterion,” Vibroengineering PROCEDIA, vol. 42, pp. 125–131, May 2022, doi: 10.21595/vp.2022.22541.

Copy IEEE

Copied to clipboard!

Ping, Wang. “Elastic-Plastic Solution of Circular Hydraulic Pressure Tunnel Based on D-P Criterion.” Vibroengineering PROCEDIA 42 (May 16, 2022): 125–31. https://doi.org/10.21595/vp.2022.22541.

Copy Chicago

Copied to clipboard!

Elastic-plastic solution of circular hydraulic pressure tunnel based on D-P criterion

Abstract

1. Introduction

2. Elastic-plastic solution of circular tunnels

2.1. Stress solutions

2.2. Deformation calculation

2.3. The tangential stress as the first principle stress

2.3.1. Stress solutions

2.3.2. Deformation calculation

3. Model validation and example analysis

3.1. Model validation

3.2. Example analysis

4. Conclusions

References

About this article

Related Articles