Abstract
By analyzing and studying the deduced theory of the surrounding plastic zone in the circular mining roadway, it is found that the radius of the surrounding plastic zone in the roadway considering the influence of mining coefficient can be divided into two stages: In the first stage, when the mining coefficient is small, the radius of the plastic zone is less sensitive to the mining coefficient, and the process increases linearly with the gradual increase of the mining coefficient. In the second stage, when the mining coefficient increases to a certain extent, the sensitivity of the radius of the plastic zone to the mining coefficient increases rapidly, and the non-linearity increases rapidly with the increase of the mining coefficient. With the gradual increase of the mining coefficient, the geometrical distribution morphology of the surrounding plastic zone of the roadway varies from circular to ellipse to round rectangle to butterfly, and the larger the mining coefficient, the more easily the surrounding rock is butterfly plastic zone, and the developmental dimension and range of the butterfly-leaf are larger. The growth of the buried depth of the roadway and the decrease of the cohesion and internal friction angle of the surrounding rock will lead to an increase in the radius of the plastic zone. With the rise of the mining coefficient, the sensitivity of the plastic zone radius to the buried depth of the roadway, cohesion and internal friction angle gradually enhanced. The butterfly plastic zone of the mining roadway has directional, and the butterfly-leaf will rotate to different degrees with the change of the principal stress direction of the surrounding rock of the roadway, When the maximum depth of butterfly-leaf plastic zone is located directly above the roof of roadway, the roof stability is the worst, and roof caving is easy to occur, thus, the support should be strengthened.
Highlights
- The implicit boundary equation of the surrounding rock plastic zone in the mining circular roadway is derived.
- The geometric distribution morphology characteristics of the surrounding plastic zone in the circular mining roadway are studied.
- The sensitive degree of mining coefficient, roadway depth, rock cohesion and internal friction angle on the plastic zone is analyzed.
- The butterfly plastic zone of the mining roadway has directionality.
- The relation between butterfly-leaf plastic zone and roof stability of roadway is discussed.
1. Introduction
The coal mine roadways of 70 % to 80 % are affected by different degrees of mining, and the mining stress generated during the coal seam mining is generally 2 to 3 times higher than the primary rock stress [1]. Affected by mining, the part of the surrounding rock of the coal mass enters the pressurized state from the primary stress state. Under the dual influence of mining stress and primary rock stress, the surrounding rock of coal roadway during service period has a series of engineering response characteristics such as asymmetry and large-scale instability failure, and the roof fall and rib spalling disasters frequently occur, which poses a significant threat to coal mine safety production, and the control problem of surrounding rock deformation and instability is extremely prominent. Therefore, it is the basis and key to carrying out scientific support design to grasp the mechanics mechanism of deformation and failure of surrounding rock in mining roadway. For a long time, the radius of the plastic zone of a circular roadway has been calculated using the modified Fenner (1938) or Kastner (1951) formula with the Mohr-Coulomb strength criterion as the limit equilibrium condition, and based on the volume-invariant hypothesis after rock failure and ideal elastic-plastic model, the analytical solution of the plastic zone radius R of the roadway surrounding rock under biaxial equal stress is calculated, It is found that the boundary of the surrounding plastic zone of the roadway is circle and approximately oval, both formulas are applicable to ideal elastic-plastic rock masses [2, 3]. Wang et al. [4] conducted an in-depth study on the deformation and failure mechanism of the surrounding rock under deep high stress environment from the perspective of the plastic zone, it is held that the deformation and failure of the surrounding rock is essentially caused by the formation and expansion of the plastic zone of the surrounding rock, and the extension of the plastic zone determines the degree and mode of failure of surrounding rock. Yuan et al. [5] through theoretical analysis and numerical calculation analysis found that the uneven and uncoordinated deformation of the surrounding rock of the roadway is mainly caused by the malignant expansion of the plastic zone, and controlling the expansion mode of the plastic zone is an effective way for maintaining the stability of the surrounding rock of the roadway. Ma and Yu et al. [6-8] based on the eccentric stress theory of elastic-plastic mechanics and plastic mechanics, derived the calculation formula of the deviating stress of surrounding rock in circular roadway under non-uniform stress field and the calculation method of plastic zone radius. It was found that the plastic zone radius was closely related to the angle of polar coordinates and deviating stress and was irregular distribution. Zhao et al. [9] based on the unified strength theory, derived the boundary line equation of the surrounding rock plastic zone of the non-uniform stress field, and it can be used to prediction the plastic zone dimensions and shape of the deep roadway under different lateral pressure coefficients. Zhu et al. [10] assumes that the rock mass is an ideal plastic material, and uses the Drucker-Prager criterion to analyze the relationship between the lateral pressure in the in-situ stress field and the plastic zone of the surrounding rock. Zha et al. [11] investigated the influence of mining stress and lateral pressure coefficient on the plastic zone of surrounding rock in the semi-circular arched roadway with elastic-plastic theory, M-C criterion and modified “equivalent radius” based on measured in-situ stress. Zareifard et al. [12] deduced the analytical solution of displacement and stress in the elastic-brittle-plastic analysis of circular tunnels, found that the plastic zone under uniform stress state has a great influence on the stability of roadway surrounding rock. Pan [13] believed that, for a circular roadway, the symmetrical plastic zone can exist only if the stress ratio 1. Since the initial stress state is different from the hydrostatic pressure state, the initial stress is smaller along the direction of the plastic zone expansion direction. For elliptically shaped roadway, when the initial minimum principal stress is along the long axis of the ellipse, the plastic zone exhibits a distinct uneven distribution and expands along the initial minimum principal stress. Lu [14] noted that the radius of the plastic zone of the roadway surrounding rock mainly depends on the vertical principal stress. Only when the horizontal principal stress exceeds a specific critical value, the radius of the plastic zone will increase with the increase of the horizontal principal stress. Xiang et al. [15] found that when the pile foundation load changes much, it will significantly affect the range and shape of the surrounding plastic zone of the shallow tunnel. Zhao et al. [16] carried out cyclic incremental loading and unloading experiments on the hard rock under various confining pressure conditions, found that higher deviatoric stress is the main cause of plastic failure of the rock mass. Yao [17] studied the plasticity of the crack tip and obtained some new understandings: the formation of the plastic zone is mainly to absorb the excess energy generated by the fracture flow, which makes the rock crack more difficult to propagate and expand when plastic deformation occurs. Karampinos et al. [18] studied the effect of plastic zone expansion on stress redistribution of surrounding rock in hard rock roadway based on field measurements. Hadjigeorgiou et al. [19] used numerical simulation method to study the distribution of plastic zones in different excavation sequences and the control of plastic bars in different performance bolts based on the actual situation on site. Wang et al. [20] studied the control effect of full-section anchor spray reinforcement technology on surrounding rock of loose fractured roadway from the perspective of controlling the range of plastic zone. Xie et al. [21] used the strain softening model to study the evolution law of the plastic zone surrounding rock in the whole process of working face propulsion. Based on the asymmetric distribution characteristics of the plastic zone surrounding the roadway, the partitioned asymmetric surrounding rock control technology was proposed. The above research results mainly focus on the study of the influence law of the primary rock stress on the plastic zone of the surrounding rock of the roadway, without considering the influence mechanism of the mining on the plastic zone of the surrounding rock in the process of coal seam mining, so it cannot truly reflect the deformation and instability evolution mechanism of the surrounding rock of the mining roadway, and cannot put forward the effective policy supporting measures of the surrounding rock of the mining roadway. This paper is based on elastic-plastic theory and Mohr-Coulomb strength theory, the parameters of the mining coefficient are introduced, and the mechanical analysis model of the surrounding rock in a circular mining roadway is established, the implicit boundary equation of the surrounding rock plastic zone of the mining circular roadway is derived, and the geometric distribution morphology characteristics of the surrounding plastic zone of the mining roadway are studied, and the influence degree of mining coefficient, roadway depth, surrounding rock cohesion and internal friction angle on the plastic zone is analyzed.
2. Theoretical analysis of the plastic zone of surrounding rock in mining roadway
2.1. Mechanical model of circular mining roadway
The surrounding rock of mining roadway is not an ideal uniform stress environment. Before being affected by mining, the deformation of the surrounding rock of the roadway tends to be relatively small. After being influenced by mining, the surrounding rock stress around the roadway increased sharply, and the roadway deformation and failure were severe. At the same time, a large number of anchor cables broke and failed, and the roof fall accident occurred frequently. Therefore, it is of great engineering practical significance to study the elastic-plastic analytical solution of circular roadway undermining conditions.
For the analysis of the influence of mining on the coal mine roadway, the mining coefficient (indicating the degree of impact of mining on the principal stress field of the primary rock) is introduced in the model analysis, and the following underlying assumptions are made:
(1) The roadway is a circular infinite long drift with a radius and a buried depth ≥ 20;
(2) The surrounding rock of the roadway is an ideal elastic-plastic body of the isotropic and uniform medium;
(3) Regardless of the spatial effect of the excavation face of the roadway and the support reaction force;
(4) The external boundary conditions are vertical principal stress and horizontal principal stress , both of which are parallel to the Cartesian coordinate axis and are equal in dimension.
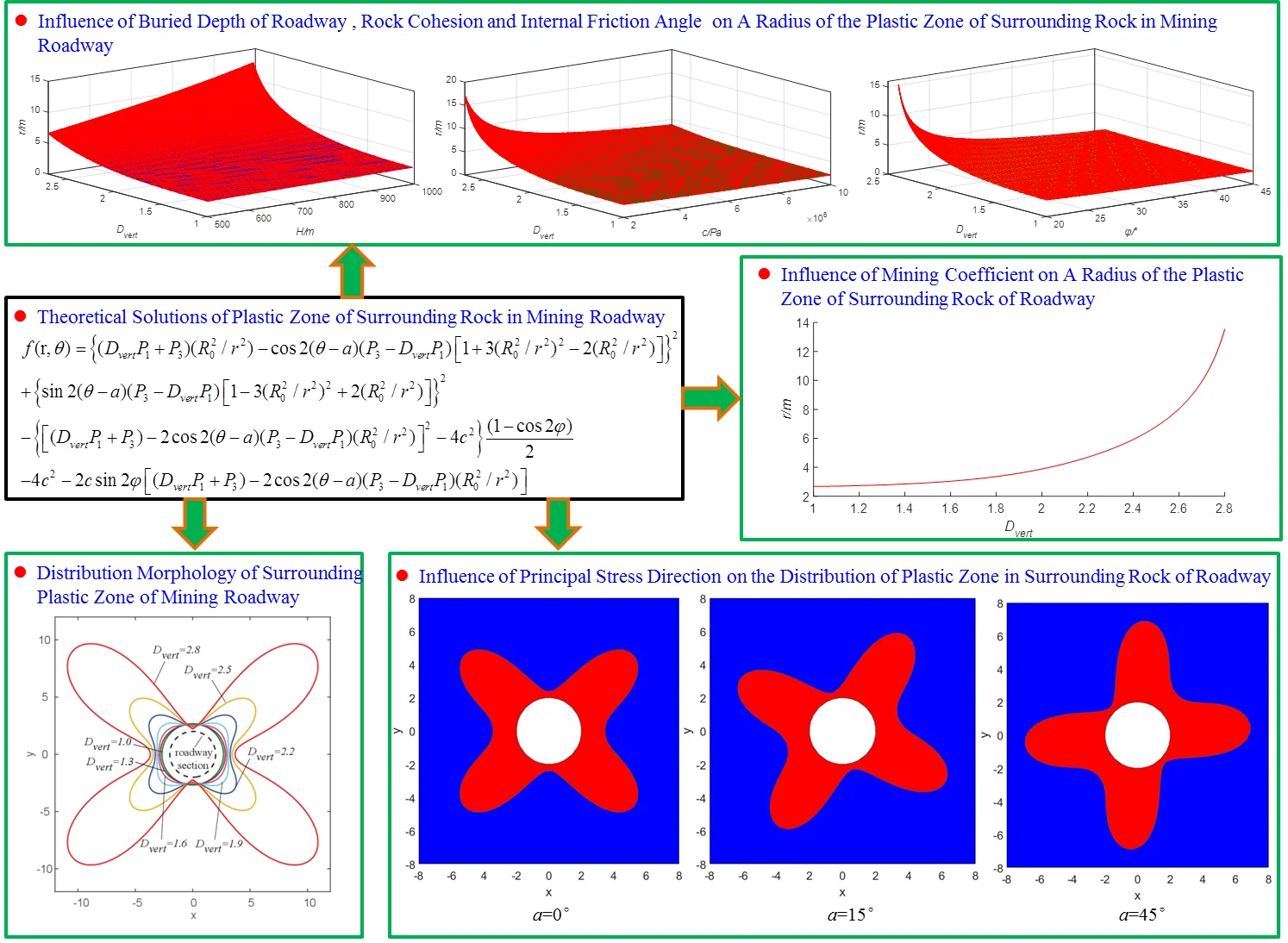
Base on the above assumptions, the method of plane strain problem can be adopted, and any section of the roadway is taken as its representative for research. In this way, the actual roadway model can be simplified to the plane strain problem of the circular hole in which the load and the structure of the elastic-plastic mechanics are axially symmetric. Depending on this, the mechanical model of the surrounding rock in the mining circular roadway is shown in Fig. 1.
2.2. Theoretical solutions of plastic zone of surrounding rock in mining roadway
For the feasibility of theoretical calculation, according to the established circular roadway mechanical model, it is assumed that the surrounding rock of the roadway is not affected by geological structure, water, rock structure and other factors, and the ground stress field is only composed of the self-heavy stress field. The surrounding rock pressure of the mining roadway in Fig. 1 can be decomposed into two cases (a) and (b) as shown in Fig. 2.
For case Fig. 2(a), according to the elastic theory [22], the elastic stress field of a uniform pressure circular roadway with radius is:
In the formula, and are the radial stress and hoop stress at any point of the surrounding rock of the circular roadway under polar coordinates; is the polar coordinate of the position.
For case (b), the surrounding rock stress field of the circular roadway is:
In the formula, is the shear stress at any point of the surrounding rock of the roadway in polar coordinates; is the polar coordinate of the position.
Fig. 1Pressure model of mining roadway
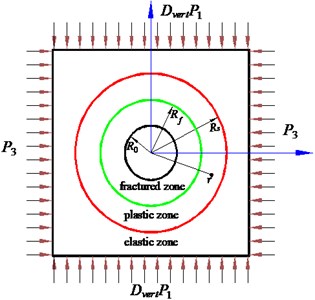
Fig. 2Pressure decomposition of the surrounding rock in mining roadway
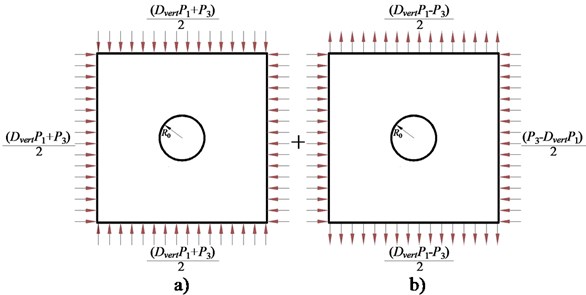
By superimposing the stress fields in the above two cases, the elastic stress field of the surrounding rock in the circular roadway can be obtained under the condition of the non-uniform stress field. The specific expression is as follows:
Combined with the literature [23], the polar coordinate expression of the Mohr-Coulomb strength criterion is:
In the formula, is the cohesion, MPa; is the internal friction angle (°).
Assume that the plastic zone boundary is , and bring the Eq. (4) into Eq. (3) to derive the implicit equation of the boundary of the surrounding plastic zone of the circular roadway with , , namely:
The above Eq. (5) considers that the magnitude of the principal stress in the surrounding rock area of the circular roadway changes, but the direction does not vary. Field measurements have shown that mining will not only change the principal stress of the surrounding rock around in the roadway but also cause a certain degree of change in the principal stress direction [24]. According to the surrounding rock stress environment of the circular roadway, combined with the theory of elastic mechanics and Eq. (5), the implicit boundary equation of the surrounding plastic zone of the circular roadway with the two factors of principal stress and direction can be obtained, namely:
In the formula, is the angle between the maximum principal stress and the vertical direction (clockwise is positive), (°).
3. Distribution law of surrounding plastic zone of mining roadway
3.1. Distribution morphology of surrounding plastic zone of mining roadway
According to the analytical formula of the plastic zone boundary of the surrounding rock in the circular mining roadway of Eq. (6), the impact of mining on the geometrical distribution and evolution process of the surrounding plastic zone of the roadway can be analyzed. According to Eq. (6), the computer program is programmed by MATLAB to draw a graph of the relationship between the plastic zone boundary of the roadway surrounding rock, and the mining coefficient can be drawn (Fig. 3). In Fig. 3, 2 m, 3 MPa, 25°, 0°, 20 MPa.
Fig. 3Morphological distribution characteristics of the plastic zone in the surrounding rock of mining roadway
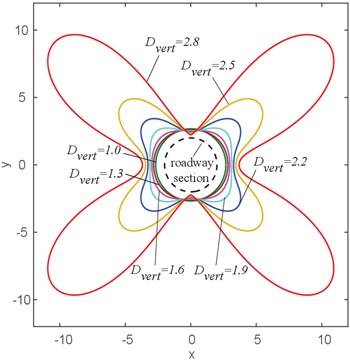
It can be seen from Fig. 3 that when the mining coefficient is equal to 1 (regardless of the mining effect), the plastic zone distribution of the surrounding rock of the circular roadway under the uniform stress field is circular. With the gradual increase of the mining coefficient, the plastic zone in the horizontal direction increases slowly, and the plastic zone in the vertical direction decreases gradually, the regular distribution of the plastic zone changes from round to oval to round rectangle to butterfly. When the butterfly plastic zone of the surrounding rock is formed, with the increase of the mining coefficient, the expansion mode of the plastic zone is mainly based on the rapid expansion of the butterfly-leaf, supplemented by other parts. The butterfly plastic zone has four symmetrical butterfly-leaf (the largest dimension portion of the butterfly plastic zone).
3.2. Influence of mining coefficient on a radius of the plastic zone of surrounding rock of roadway
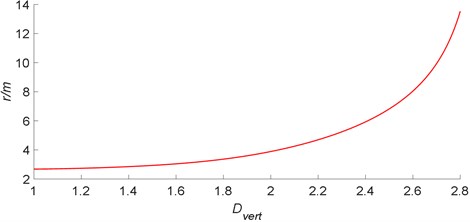
According to Eq. (6), the computer program is programmed by MATLAB to draw a graph of the relationship between the radius of the surrounding plastic zone of the circular roadway and the mining coefficient (Fig. 4).
As can be seen from Fig.4, the effect of the mining coefficient on the radius of the plastic zone can be divided into two phases. The first stage, with the gradual increase of the mining coefficient, the radius of the plastic zone slowly increases, which increases approximately linearly. The plastic zone radius at this stage is less sensitive to the mining coefficient. For example, when the mining coefficient is increased from 1.3 to 1.6, the radius of the plastic zone is only increased by 0.3 m. When the mining coefficient continues to expand and enter the second stage, the rate of change of the radius of the plastic zone is rapidly growing, and the curve is “rapid head-up type”, and the plastic zone is malignantly expanded. For example, when the mining coefficient is increased from 2.5 to 2.8, the radius of the plastic zone increases rapidly from 7 m to 14 m, and the butterfly-leaf dimension increases by two times, this indicates that the plastic yield failure of the surrounding rock mass in this range is very sensitive to the mining coefficient. Even if the mining coefficient does not change much, it may cause localization of the deformation and failure of the surrounding rock. The formation and nonlinear expansion of the butterfly-leaf in the plastic zone have theoretically proved that the shear deformation and failure of the two corners and the bottom edge of the mining roadway are often found in the field investigation. At the same time, it also fully shows that the mining roadway is more deformed and more challenging to control than the ordinary roadway.
Fig. 4The relationship between a radius of the plastic zone and mining coefficient of surrounding rock in mining roadway
3.3. Influence of buried depth of roadway on a radius of the plastic zone of surrounding rock in mining roadway
The buried depth of the roadway is increased from 500 m to 1000 m, and keep the same parameters as in Section 3.1. Calculated according to Eq. (6) and equation , the computer program is programmed by MATLAB to draw a graph of the relationship between the radius of the surrounding plastic zone of the mining roadway and the buried depth of the roadway (Fig. 5). Among them, the primary rock stress the rock mass density 2500 kg/m3, and the gravitational acceleration 10 N/kg.
It can be observed in Fig. 5 that with the increase of the buried depth of the roadway, the radius of the plastic zone of the surrounding rock increases linearly, showing a linear relationship between both. When the mining coefficient is small, the sensitivity of the plastic zone radius to the buried depth of the roadway is relatively weak.
Fig. 5The relationship between the plastic zone radius of the surrounding rock and the buried depth in mining roadway
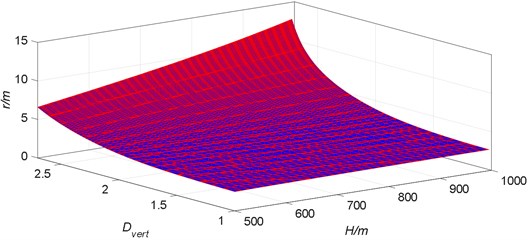
For example, when the mining coefficient is 1.5, the radius of the plastic zone when the depth of the roadway is changed from 500 m to 1000 m is only increased by 0.3 m. With the gradual increase of the mining coefficient, the sensitivity of the plastic zone radius to the buried depth of the roadway is gradually enhanced. For example, when the mining coefficient is 2.7, the roadway depth changes from 500 m to 1000 m, the plastic zone radius increases rapidly from 4.5 m to 13 m, and the butterfly leaf size increases by 8.5 m.
3.4. Influence of cohesion on the radius of the plastic zone of surrounding rock in mining roadway
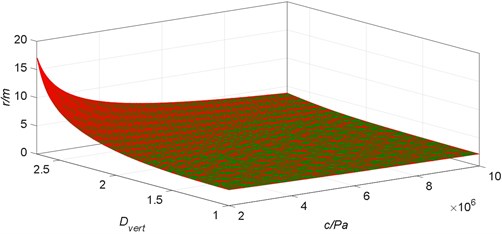
The cohesion of the surrounding rock of the roadway is reduced from 10 MPa to 2 MPa, and keep the same parameters as in Section 3.1. According to Eq. (6), the computer program is programmed by MATLAB to draw a graph of the relationship between the radius of the surrounding plastic zone of the mining roadway and the cohesion of the surrounding rock (Fig. 6).
It can be observed in Fig. 6 that when the mining coefficient is small, the radius of the plastic zone of the surrounding rock increases approximately linearly with the decrease of the cohesive force, which shows an approximately linear relationship between the both. However, the plastic zone radius is relatively less sensitive to cohesion. For example, when the mining coefficient is 1.5, the radius of the plastic zone when the cohesion is reduced from 10 MPa to 2 MPa is only increased by 0.7 m. As the mining coefficient increases, the approximately linear relationship between the radius of the plastic zone and the cohesive force gradually changes to a nonlinear relationship, and the sensitivity of the plastic zone radius to the cohesion is gradually enhanced. For example, when the mining coefficient is 2.6, the cohesion is reduced from 10 MPa to 2 MPa, the radius of the plastic zone is rapidly increased from 3.5 m to 11.5 m, and the butterfly leaf dimension is increased by 8 m.
Fig. 6The relationship between a radius of the plastic zone and cohesion of surrounding rock in mining roadway
3.5. Influence of internal friction angle on a radius of the plastic zone of surrounding rock in mining roadway
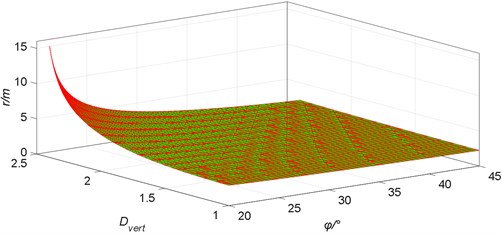
The friction angle of the surrounding rock of the roadway is reduced from 45° to 20°, and keep the same parameters as in Section 3.1. According to Eq. (6), the computer program is programmed by MATLAB to draw a graph of the relationship between the radius of the surrounding plastic zone of the mining roadway and the friction angle of the surrounding rock (Fig. 7).
It can be seen from Fig. 7 that when the mining coefficient is small, the radius of the plastic zone of the surrounding rock increases approximately linearly with the decrease of the internal friction angle, which shows an approximately linear relationship between the both. However, the radius of the plastic zone is relatively weak to the internal friction angle. For example, when the mining coefficient is 1.5, the radius of the plastic zone when the internal friction angle is reduced from 45° to 20° is only increased by 1.0 m. As the mining coefficient increases, the approximately linear relationship between the plastic zone radius and the internal friction angle gradually changes to a nonlinear relationship, and the sensitivity of the plastic zone radius to the internal friction angle steadily increases. For example, when the mining coefficient is 2.6, the internal friction angle is reduced from 45° to 20°, the plastic zone radius is rapidly increased from 2.8 m to 10.0 m, and the butterfly leaf dimension is increased by 7.8 m.
Fig. 7The relationship between a radius of the plastic zone and internal friction angle of surrounding rock in mining roadway
4. Influence of principal stress direction on the distribution of plastic zone in surrounding rock of roadway
Due to the temporal-spatial relationship between the coal mine roadway and the working face during mining, the magnitude and direction of the principal stress of the surrounding rock around the roadway will change with the evolution of the mining [25]. The effect of mining on the surrounding rock of the roadway is mainly reflected in two aspects. On the one hand, the stress of the surrounding rock around the roadway is changed, so that the vertical stress of the surrounding rock around the roadway increases sharply in a short time, resulting in large deformation of the surrounding rock of the roadway. On the other hand, the principal stress direction of the surrounding rock around the roadway is deflected, resulting in asymmetrical deformation of the surrounding rock of the roadway, and the frequency of roof fall increases.
According to Eq. (6), the distribution pattern of the plastic zone of the surrounding rock of the roadway is drawn utilizing MATLAB computer program (Fig. 8).
As shown in Fig. 8, when the maximum confining pressure produced by mining effect on the surrounding rock of roadway is vertical ( 0°), the plastic zone of the surrounding rock of roadway is butterfly, and the butterfly leaf are located near the angular bisectors of the two principal stress directions, that is, the butterfly leaf in the butterfly plastic zone is directional. As the direction of the maximum principal stress changes, the position of the butterfly leaf in the butterfly plastic zone also changes. When the direction of the principal stress is not horizontal or vertical, the region of the butterfly leaf in the butterfly plastic zone will be located on the roof of the roadway, at this time, the roof has the largest depth of damage and is prone to roof failure (Fig. 8(d)).
When there is a larger plastic zone above the roadway, there is a risk of the roof falling off the roadway, and the range of the plastic zone is also the range of the potential collapsed zone. The plastic zone above the roadway just is called potential caving zone because the plastic zone of roof surrounding rock is produced, but it does not necessarily mean that the roof surrounding rock must cave. After the plastic failure of the surrounding rock, the concave and convex rupture surfaces inside the ruptured surrounding rock mass are inter-occlusion, and there is frictional resistance between them, and still has a specific bearing capacity. If it is not timely supported or the support is unreasonable, when it is strongly mine, the ruptured surrounding rock mass of the roof of the roadway is easy to fall under the effect of its weight, and the stability of the roof is the worst at this time. Plastic zone failure depth above the roof level of the roadway is the height of the potential caving zone, and the length of the butterfly leaf in the plastic zone of the roadway is the maximum plastic failure depth. Therefore, the regular distribution of the surrounding plastic zone of the roadway is different, and the shape and extent of the potential caving zone of the roof of the roadway are also different.
Fig. 8The relationship between the shape of the butterfly plastic zone and the principal stress direction of the surrounding rock of the roadway
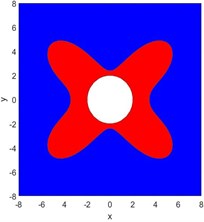
a) 0°
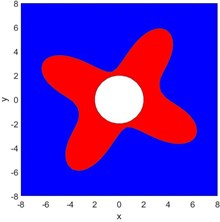
b) 15°
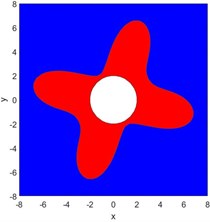
c) 30°

d) 45°
5. Conclusions
Deformation and damage of surrounding rock in mining roadway has always been a major problem that plagues and restricts safe and efficient mining of mines. The deformation and failure of the roadway are caused by the formation and expansion of the plastic zone of the surrounding rock. The expansion of the plastic zone determines the degree of damage and mode of the surrounding rock. Therefore, it is of great theoretical significance and engineering practical value to study the geometrical distribution characteristics of the surrounding plastic zone of the mining roadway and to analyze the degree of influence of mining coefficient, roadway depth, surrounding rock cohesion and internal friction angle on plastic zone to control the surrounding rock of the roadway and prevent and control the roof disaster.
1) The implicit equation of the boundary of the plastic zone surrounding the circular roadway is obtained. It is found that with the gradual increase of the mining coefficient, the regular distribution of the surrounding plastic zone of the roadway varies from circular to elliptical to round rectangle to butterfly. The butterfly plastic zone has four symmetrical butterfly-leaf (the most significant part of the butterfly plastic zone), and with the increase of the mining coefficient, the expansion mode of the plastic zone is mainly based on the rapid expansion of the butterfly-leaf, and the other parts are supplements.
2) The influence of the mining coefficient on the radius of the plastic zone of the roadway surrounding rock is divided into two stages. In the first stage, with the gradual increase of the mining coefficient, the radius of the plastic zone slowly increases, which increases approximately linearly, and the range of the plastic zone is less sensitive to the mining coefficient. In the second stage, when the mining coefficient increases to a certain extent, the rate of change of the plastic zone radius increases rapidly, the sensitivity of the plastic zone radius to the mining coefficient increases quickly, and the plastic zone produces a malignant expansion.
3) The growth of the buried depth of the roadway and the decrease of the cohesion and internal friction angle of the surrounding rock will lead to an increase in the radius of the plastic zone. With the rise of the mining coefficient, the sensitivity of the plastic zone radius to the buried depth of the roadway, cohesion and internal friction angle gradually enhanced.
4) The butterfly plastic zone of the mining roadway has directionality, and the position of the butterfly-leaf will rotate to different degrees with the change of the principal stress direction of the surrounding rock of the roadway. When the maximum depth of butterfly-leaf plastic zone is located directly above the roof of the roadway, the roof stability is the worst, and roof fall is easy to occur, so the support should be strengthened. The plastic zone range at this time is also the range of the potential caving zone of the roof of the roadway. Acoustic emission and other detecting instruments can be used to detect the plastic range of the surrounding rock of the mining roadway roof and provide guidance for preventing the roadway from falling.
References
-
Xie H. P., Zhang Z. T., Gao F., et al. Stress-fracture-seepage field behavior of coal under different mining layouts. Journal of China Coal Society, Vol. 41, Issue 10, 2016, p. 2405-2417.
-
Kastner H. Tunnel and Trench Statics. Shanghai Scientific and Technical Publishers, Shanghai, 1980.
-
Yong L., Cao S. G., et al. Elasto-plastic analysis of a circular borehole in elastic-strain softening coal seams. International Journal of Rock Mechanics and Mining Sciences, Vol. 10, 2015, p. 316-324.
-
Wang W. J., Guo G. G., Zhu Y. J., et al. Malignant development process of the plastic zone and control technology of high stress and soft rock roadway. Journal of China Coal Society, Vol. 40, Issue 12, 2015, p. 2747-2754.
-
Yuan C., Wang W. J., Feng T., et al. Research on control principles of surrounding rocks of the roadway based on the expansion of plastic zone. Journal of Mining and Safety Engineering, Vol. 34, Issue 6, 2017, p. 1051-1059.
-
Ma N. J., Li J., Zhao Z. Q., et al. Distribution of the deviatoric stress field and plastic zone in circular roadway surrounding rock. Journal of China University of Mining and Technology, Vol. 44, Issue 2, 2015, p. 206-213.
-
Yu W. J., Liu F. F. Stability of close chambers surrounding rock in deep and comprehensive control technology. Advances in Civil Engineering, Vol. 2018, 2018, p. 6275941.
-
Yu W. J., Wu G. S., An B. F. Investigations of support failure and combined support for soft and fractured coal-rock tunnel in tectonic belt. Geotechnical and Geological Engineering, Vol. 36, Issue 6, 2018, p. 3911-3929.
-
Zhao Z. Q. Mechanism of Surrounding Rock Deformation and Failure and Control Method Research in Large Deformation Mining Roadway. China University of Mining and Technology, Beijing, 2014.
-
Zhu Y. W., Huang K. J., Li W. Study on effect of in-situ stresses on plastic region induced by excavations of underground openings. Chinese Journal of Rock Mechanics and Engineering, Vol. 23, Issue 8, 2004, p. 1344-1348.
-
Zha W. H., Hua X. Z., Chen D. H. Quantitative analysis of the plastic region in the deeply buried tunnel based on the in-situ stress test. Journal of Experimental Mechanics, Vol. 28, Issue 5, 2013, p. 657-662.
-
Zareifard M. R., Fahimifar A. Analytical solutions for the stresses and deformations of deep tunnels in an elastic-brittle-plastic rock mass considering the damaged zone. Tunnelling and Underground Space Technology, Vol. 58, 2016, p. 186-196.
-
Pan Y. W., Chen Y. M. Plastic zones and characteristics-line families for openings in elasto-plastic rock mass. Rock Mechanics and Rock Engineering, Vol. 23, 1990, p. 275-292.
-
Lu A. Z., Xu G. S., Sun F., et al. Elasto-plastic analysis of a circular tunnel including the effect of the axial in-situ stress. International Journal of Rock Mechanics and Mining Sciences, Vol. 47, 2010, p. 50-59.
-
Xiang Y. Y., Feng S. Q. Theoretical prediction of the potential plastic zone of shallow tunneling in the vicinity of pile foundation in soils. Tunnelling and Underground Space Technology, Vol. 38, 2013, p. 115-124.
-
Zhao Y. L., Wang Y. X., Wang W. J., Wan W., Tang J. Z. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. International Journal of Rock Mechanics and Mining Sciences, Vol. 93, 2017, p. 66-75.
-
Yao Y. Linear elastic and cohesive fracture analysis to model hydraulic fracture in brittle and ductile rocks. Rock Mechanics and Rock Engineering, Vol. 45, 2012, p. 375-387.
-
Karampinos E., Hadjigeorgiou J., Hazzard J., Turcotte P. Discrete element modelling of the buckling phenomenon in deep hard rock mines. International Journal of Rock Mechanics and Mining Sciences, Vol. 80, 2015, p. 346-356.
-
Hadjigeorgiou J., Karampinos E. Use of predictive numerical models in exploring new reinforcement options for mining drives. Tunnelling and Underground Space Technology, Vol. 67, 2017, p. 27-38.
-
Wang F. T., Zhang C., Wei S. F., Zhang X. G., Guo S. H. Whole section anchor–grouting reinforcement technology and its application in underground roadways with loose and fractured surrounding rock. Tunnelling and Underground Space Technology, Vol. 51, 2016, p. 133-143.
-
Xie S. R., Yue S. S., Chen D. D., et al. Deviatoric stress evolution laws and control of surrounding rock at gob-side entry retaining in deep backfilling mining. Journal of China Coal Society, Vol. 43, Issue 7, 2018, p. 1837-1846.
-
Xu Z. L. Concise Course of Elasticity. Fourth Edition, Higher Education Press, Beijing, 2013.
-
Zhang X. Y., Yan S. W. Basis of Geotechnical Plastic Mechanics. Tianjin University Press, Tianjin, 2004.
-
Liu J., Wang E. Y., Zhao E. L., et al. Distribution and variation of the mining-induced stress field in the deep workface. Journal of Mining and Safety Engineering, Vol. 31, Issue 1, 2014, p. 60-65.
-
Zhou G., Li Y. S., Zhang Q. A., et al. Research on monitoring technique and evolution law of the disturbance stress in Chensilou Colliery. Journal of China Coal Society, Vol. 41, Issue 5, 2016, p. 1087-1092.
Cited by
About this article
The study is supported by the National Natural Science Foundation of China (Grant Nos. 51804109; 51434006; 51874130) and the Scientific Research Foundation for Doctor of Hunan University of Science and Technology (Grant No. E51851).
