The stability analysis of blasting excavation in short distance on water diversion tunnel underpassing Jinduicheng Molybdenum Mine

1. Introduction

With the development of economic construction and infrastructure, a rising number of blasting constructions near or on the existing structures appear and it is necessary to analyze the impact of vibration caused by blasting on the existing structures or facilities. Some scholars have done some researches on the propagation of stress wave and the attenuation of blasting vibration by theoretical analysis, numerical simulation, field test and comprehensive method. Kesimal [1] presented a theoretical analysis for evaluating the influence of blast-induced acceleration on the stability of slopes. Yan [2] employed a two-dimensional circular theoretical model to investigate the stress evolution and rock damage caused by millisecond-delay blasting. Shin [3] investigated the characteristic behavior of existing tunnels by utilizing the numerical method. Parametric analyses were conducted under various conditions to analyze the screening effectiveness of line-drilling [4]. The results of vibration analysis induced by blasting were performed to obtain the particle vibration velocities, the empirical relationships between scaled distance and peak particle velocity and the interaction between shotcrete and rock influenced by propagating stress waves [5]. Singh [6] investigated the effect of heavy blasting in open-pit coal mines on the stability of adjacent underground coal mine workings. Ongen [7] employed various estimation models to assess the effect of blast-induced vibration. Moreover, many scholars utilized LSDYNA to investigate the effects and characteristics of blast loading induced by detonation of explosives [8-10].

The influence of mine blasting on the safety of adjacent structures is an important issue. Dongchuan River diversion tunnel is a necessary River Diversion Project for the South expansion of open-pit mine, part of which is located below the mining area of Jinduicheng Open-pit Mine. The surrounding rock of the tunnel has complex structure, poor stability and is close to the open-pit stope. The unloading and blasting vibration caused by the daily mining of the mine has adverse effects on the safety of the tunnel.

In this paper, blasting monitoring of tunnel has been designed and carried out in order to ensure the safety of tunnel in mining process. Comparing with the monitoring results, the vibration and failure characteristics of tunnel lining structure and surrounding rock under the influence of blasting load are analyzed by numerical software FLAC^3D, and the development trend may be forecasted, so that the late mining plan can be determined to guide mine production.

2. Project overview

The total length of Dongchuan River, originating from the eastern high mountain area, and flowing through the eastern mining area, is about 9.5 km. Due to implementation the plan of south extension of open-pit mine, the Dongchuan River is converted into the Dongchuan River Diversion tunnel with dimensions 1280×6×7 m, and the lining thickness is from 30 mm to 50 mm. The diversion tunnel located in the northern margin of the Qinling axis in the Cambrian-Sinian sag zone has an extremely complicated geological condition. Its surrounding rock is mainly hard andesitic porphyrite and quartz rock together with high strength, poor integrity and mostly scattered-fragmented structure. Additionally, the local areas present granular structure. Therefore, it is a typical hard brittle broken surrounding rock coupled with rock grade IV-V. Extensive folds and faults are extremely developed and the developed fissure water makes the stability of surrounding rock worse. The minimum horizontal and vertical distances between the tunnel and the open-pit mine are 125 m and 70 m, respectively, and the vibration induced by mine blasting will have an adverse effect on the safe operation of the tunnel.

3. The analysis of tunnel stability

3.1. The monitoring scheme

The Diversion Tunnel is located below the southern open-pit blasting area coupled with the altitude difference between 70 m and 110 m. The height of the bench of blasting zone is 12 m, and the slope angle of the bench is 69 degrees. The pitch distance and row spacing of the vertical hole together with 7×9 m in the blasting area is adopted. The distance of the chassis resistance line to the vertical hole is 9 m, the mixed emulsion explosive is employed and the maximum single charge of the hole is 430 kg with plug length between 5.5 m and 6.5 m and the 250 millimeter diameter. The blasting network is composed of Orica non-electric high-precision detonator tube detonator, and the corresponding delay time is 25 ms between holes, 65 or 100 ms between rows, respectively. The blasting holes arrangement is shown in Fig. 1.

Fig. 1The blasting hole arrangement

a)

b)

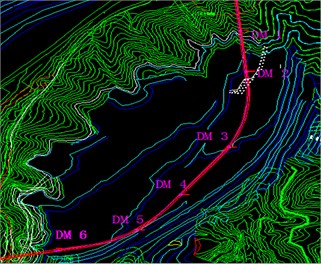
Tracking and monitoring the diversion tunnel together with the TC-4850 blasting vibration meter is implemented during the whole unloading and blasting process in open pit mining. Measuring points are mainly set according to the four dangerous locations listed in the geological structure analysis, including six monitoring sections in total and three measuring points in each section, as shown in Fig. 2, and Parts of the installation for measuring points are illustrated in Fig. 3.

Fig. 2The arrangement of monitoring at section

Fig. 3Installation of measuring points

a)

b)

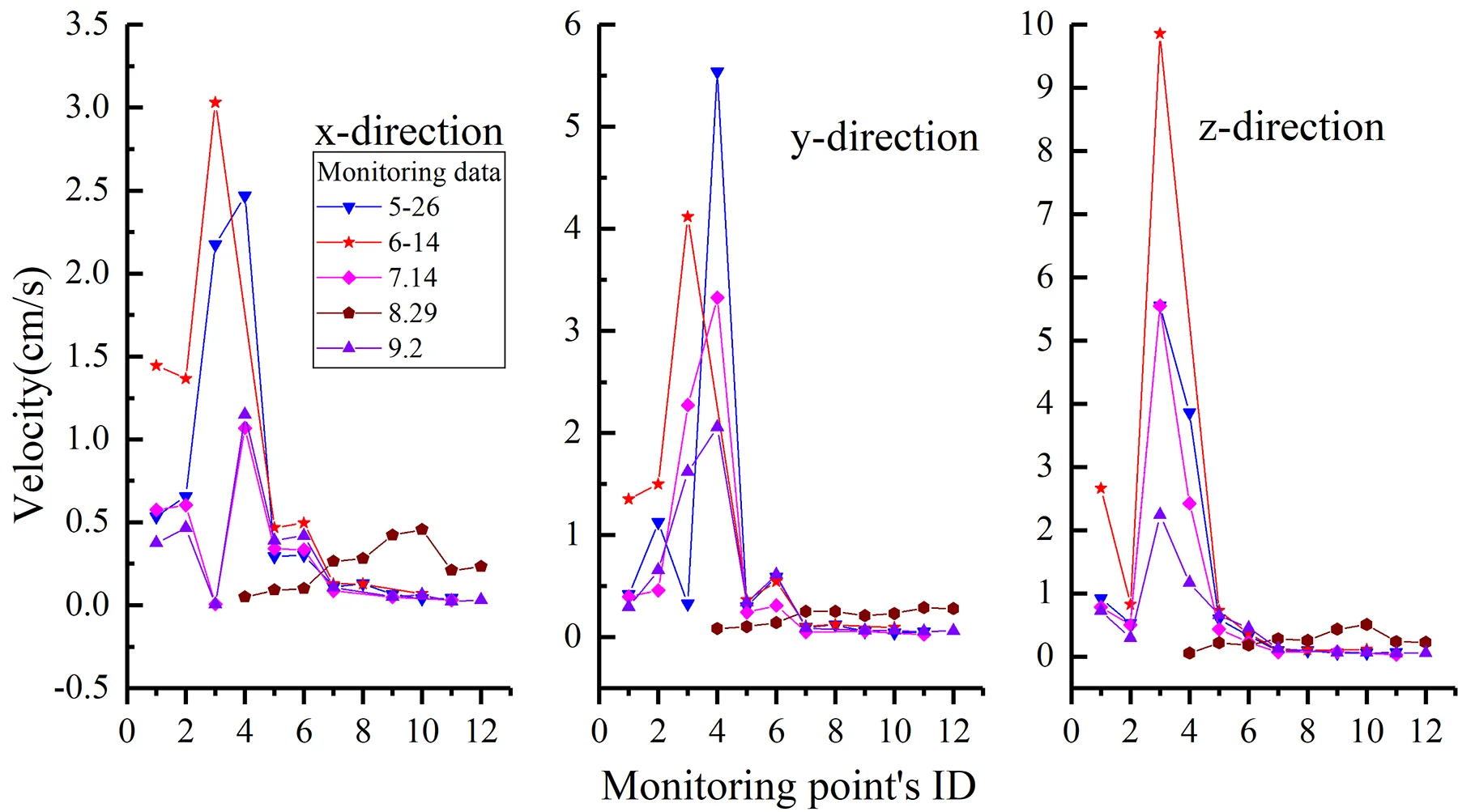
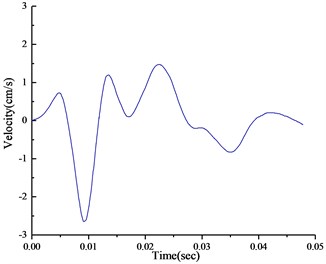
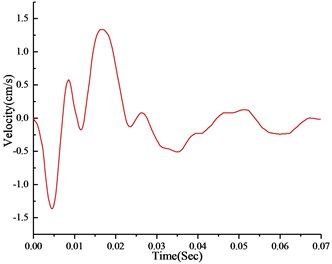
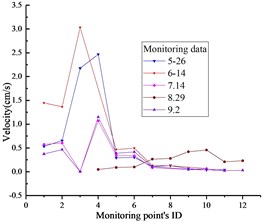
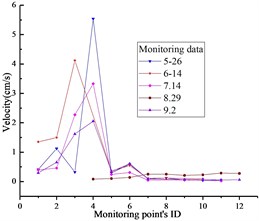
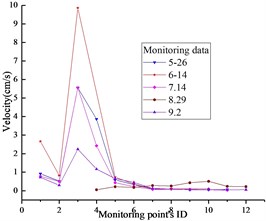
The time history of monitoring results obtained by blasting vibration meter in the typical section is given in Fig. 4. As can be seen from the illustrations, the vertical and horizontal particle peak values in this section are 2.62 cm/s and 1.26 cm/s, respectively. According to the national “blasting safety regulations”, the seismic capacity of hydraulic tunnel is 7-15 cm/s. Therefore, the PPVs illustrated in Fig. 5 don’t exceed the allowable value of the regulation.

Fig. 4Time history of velocity in the top section: a) vertical, b) horizontal

a)

b)

Fig. 5PPVs of monitoring results: a) x-direction, b) y-direction, c) z-direction

a)

b)

c)

3.2. Analysis of blasting vibration

By gradually reducing the distance between the open pit and the diversion tunnel in present analysis, the effect of blasting mining on the diversion tunnel are simulated by employing the numerical tool FLAC^3D.

3.2.1. Numerical model for calculation

Tunnel model is established according to the actual size of the section of diversion tunnel, shown in Fig. 6.

Fig. 6Numerical model for calculation

The dimension of the model is a rectangular body of 300 m×300 m×300 m. The typical section is V-grade surrounding rock, mainly including andesitic and granite. Section lining employs C25 reinforced concrete, matched with reinforcement of $\phi$16@200 and $\phi$20@200. Assuming that the material obeys the Mohr-Coulomb strength criterion together with the following parameters (in Table 1). The shear failure appears when the principal stresses meet the Mohr-Coulomb criterion:

1

$F={\sigma }_1-{\sigma }_3\frac{1+\mathrm{s}\mathrm{i}\mathrm{n}\phi }{1-\mathrm{s}\mathrm{i}\mathrm{n}\phi }-2c\sqrt{\frac{1+\mathrm{s}\mathrm{i}\mathrm{n}\phi }{1-\mathrm{s}\mathrm{i}\mathrm{n}\phi }}>0,$

where ${\sigma }_1$ and ${\sigma }_3$ are major and minimum principal stresses, respectively.

3.2.2. Determination of blasting load

The blasting load belongs to impact load, whose time history can be expressed exponential function, Gaussian function and triangular function. Extensive blasting applications still employ semi-empirical formulae and theories of blasting to evaluate the peak explosion pressure. When considering the decoupling effect, the peak pressure exerted on the blast-hole wall can approximately be described as follows [11]:

2

$P_0=\frac{{\rho }_e{D}^2}{2\left(1+\gamma \right)}{\left(\frac{a}{b}\right)}^{2\gamma },$

where $P_0$ is the blasting load peak pressure, ${\rho }_e$ is the explosive density, $D$ is the velocity of detonation, $a$ is the charge diameter, $b$ is the blast-hole diameter and $\gamma$ is the ratio of the specific heats for the detonation gases, in general, the value of $\gamma$ is 1.5.

Table 1Material parameters of surrounding rock

Material parameters	Ⅴ-grade surrounding rock	Reinforced concrete
Elastic bulk modulus $K$	265 MPa	166.7 GPa
Cohesion $c$	0.2 MPa	3.125 MPa
Dilation angle $\psi$	15°	12°
Internal friction angle $\phi$	23°	0°
Elastic shear modulus $G$	2.6 GPa	76.9 GPa
Tensile strength ${\sigma }_t$	0.5 MPa	19.1 MPa

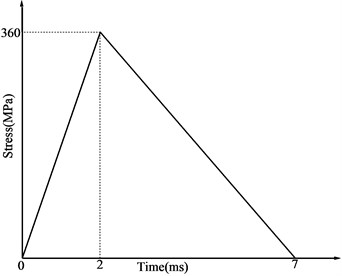
In blasting process, it is necessary to simplify blast loading curve in numerical computation and theoretical analysis. Extensive investigations concerned with blasting procedures reveal that the blasting pressure-time history can be simplified as a triangular load curve and the whole process include linear loading and linear unloading phase, which can be written by:

3

$P_w\left(t\right)=\left\{\begin{array}{ll}0,t<0,& \\ \frac{t}{t_r}{P}_0,0\le t<t_r,& \\ \frac{t_s-t}{t_s-t_r}{P}_0,t_r\le t<t_s,& \\ 0,t\ge t_s,& \end{array}\right.$

where $P_w\left(t\right)$ represents the blasting load time history, $P_0$ is the peak pressure of the blasting load, $t_r$ and $t_s$ are the rising time and total time of blasting load, respectively.

The total time of blasting load is several hundred milliseconds to a few milliseconds [12, 13]. In this project, rising time $t_r=$ 2 ms and total time $t_s=$ 7 ms are adopted, so the pressure curve of blasting load can be depicted in Fig. 7. As for damping, the Rayleigh damping is adopted, and the minimum critical damping ratio ${\xi }_{min}$ is equivalent to 0.05 and the minimum center frequency $f_{min}$ is equal to 20 Hz.

Fig. 7Pressure curve of blasting load

3.2.3. Dynamic response analysis

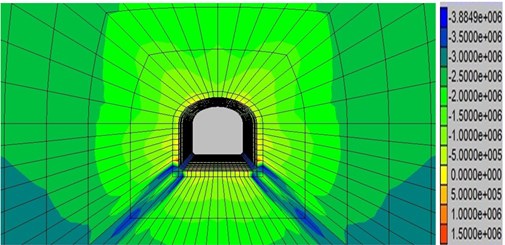
The load of the second artillery in the 14th June, 2011 is taken as the value of the blasting load. Numerical results of the particle velocity under the blasting vibration are shown in Fig. 8 and Fig. 9. These figures demonstrate that the maximum vertical vibration velocity of particle in the top of section is 2.40 cm/s and the maximum horizontal vibration velocity of the particle in the side section is 1.13 cm/s. The maximum compressive stress appearing at the tunnel bottom is 3.88 MPa, the maximum tension appearing at the top and side stress is 1.92 MPa in Fig. 10. The C25 reinforced concrete employed in the diversion tunnel compressive strength is 25 MPa, the tensile strength is 19.1 MPa. Therefore, it could be concluded that the stress is in the stress intensity range.

Fig. 8Time history of vertical vibration velocity of particles in the top of section

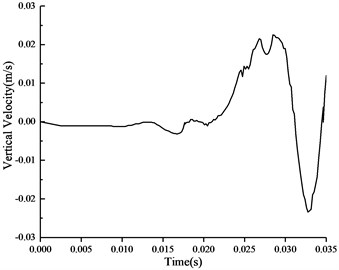
Fig. 9Time history curve of horizontal velocity of particles in the side of section

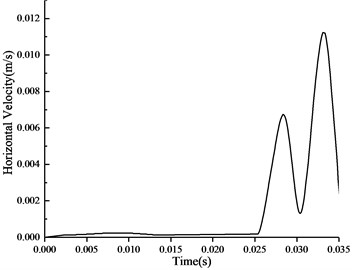
Fig. 10Contour of maximum stress in the section

3.2.4. Results analysis between monitoring results and simulation

The Table 2 presents the results regarding the comparison of monitoring results and simulated analyses. As can be observed that the error of simulation results is less than 5 %, which indicates that the simulation is correct and feasible.

Table 2Comparison of monitoring results and simulation

–	Monitoring	Simulating	Error
Peak vertical velocity (cm/s)	–2.62	–2.53	3.43 %
Peak horizontal velocity (cm/s)	–1.26	1.2	4.7 %

4. Forecast analysis

On the basis of the model, the vibration velocity of the typical section under the existing blasting scale are calculated and simulated. According to extensive simulation trial, when the minimum vertical distance decreased gradually, the vibration vertical velocity of the particle at the top of the tunnel section increased obviously. In the minimum vertical distance of 50 m, particle velocity at the top of section in vertical direction is 14.5 cm/s. The particle vibration velocity has reached the prescribed limit 15 cm/s, the corresponding measures must be taken to ensure the safety of water tunnel.

5. Conclusions

The monitoring results of Dongchuan River Diversion Tunnel and analysis of numerical dynamic simulation show that blasting has little effect on the stability of the diversion tunnel in the current mine blasting strength, simulated values and measured values differ by no more than 5 %, vibration velocity is within the range of the specification requirements.

When the minimum vertical distance is 50 m, vertical velocity of particle at the top of typical section has reached the upper safe limit of the allowable range. As the blasting area becomes closer to Dongchuan River Tunnel, blasting vibration will have destructive effects on water diversion tunnel. Therefore, according to the actual distance of stope to tunnel, we should adjust the blasting scheme of mine production, and minimize the influence of blasting vibration on the diversion tunnel to ensure safety in production.