To experimental study of performance evaluation of masonry brick bond in shear and compression in comparison

2.1. Brick

They obtained first-class bricks from three different kilns, and determined their dimensions and compressive strengths. The average size measured from brick samples was 8.9” × 4.5” × 3”. The compressive strength of three representatives from each source was determined under the specifications of ASTM C67 [38], as shown in Figs. 1, 2, and 3. These compressive strengths are reported in Table 1.

Fig. 1Schematic diagram for English bond

Fig. 2Schematic diagram for Chinese bond

Fig. 3Triplet- test specimen

2.2. Mortar

Cement is used as a binding material in mortar due to its being the most commonly used cementitious material in construction and being easily available. The mixed design of mortar considered was 1:3. Three 50 × 50 × 50 mm³ size cubes from the same mortar were cast and tested after 28 days of water curing under the specifications of ASTM C109 [39], as shown in Fig. 4 and 5. Compressive strengths of all mortar specimens are reported in Table 2.

Fig. 4Cement blocks ready for compressive strength test

Fig. 5Cement blocks ready for compressive strength test

3.1. English bond masonry prism

In English bond masonry, header and stretcher courses are laid on an alternate basis just as headers are laid centered on stretchers, and every alternate course is vertically aligned. A total of 72 two-wythes thick English bond masonry prisms with 24 prisms from each brick source were prepared in such a way that three headers with one quoin closer and two stretchers were laid on alternate courses. Among these prism specimens, each half was designated for compression strength testing and diagonal tension testing at 28 days and 56 days after water curing. The curing was done with wet jute bags in an open area at 25 °C.

The purpose of the compressive strength test of masonry prisms is to verify that materials used in masonry construction meet the specified compressive strength. This test provides a means of evaluating the compressive strength of in-place masonry by comparing it with testing of masonry prisms prepared with the same material characteristics as that of in-place masonry. The average dimension of the prisms was 16.63” × 9” × 19.825” with slight variation due to brick layout. The mean height to thickness ratio (h/t) was 2.25. Among 36 prisms nominated for a compressive strength test, 18 prisms were tested at 28 days’ water curing and the rest were tested at 56 days’ curing using UTM. Before installing the prisms in the test machine, proper capping was made on all specimens in accordance with practice C1552. The load was applied on the prism at the rate of specimens as shown in Figure 6 and 7. The correction factor against h/t of each specimen was calculated by linear interpolation between the values given in ASTM C1314 [40].

Fig. 6English bond brick column being tested for compressive strength

Fig. 7Crushed English-bond bricks column after compressive strength test

A diagonal tension test was carried out on 18 prisms at the age of 28 days and the remaining 18 prisms at 56 days water curing using UTM. The objective of this test is to measure the shear strength of a masonry prism. The mean dimension of the prisms was 28.75” × 30” × 9”, with a minor difference due to bricks orientation. Two steel loading shoes were used to apply machine load to the prism in such a way that the upper and lower loading shoes were positioned so as to be centered on the respective bearing surfaces of the machine. The length of the bearing of the shoe was 6”. The prism specimens were installed in a centered and plumb position in a bed of gypsum capping material placed in the lower loading shoe. The load was applied on the prism at the uniform rate of specimens as shown in Fig. 7. The shear strength of all the prisms is calculated from the following Eq. (1), where shear strength $S_s$, $P$ applied load, $A$ area of Specimens, $n$, numbers:

Fig. 8Testing scheme overview of English brick-bond column using UTM

Fig. 9Crushed English-bond bricks column after compressive strength test

3.2. Rat-trap bond masonry prism

The Rat-trap bond is a modular type of masonry technique that is cost-effective and environmentally friendly as compared to conventional construction due to less usage of fewer materials. It follows the brick laying pattern in such a way that, rowlock and shiner are visible on the surface of the masonry. In this kind of bond, the thickness of wall can never be less than the length of the stretcher. 72 Rat-trap bond masonry prisms with the same number of bricks from each source were made. Each half of one of these prisms was chosen for a compressive strength test and a diagonal tension test at 28 and 56 days. Rowlock and shiner are alternately placed in this type of bond to create a 3-inch cavity inside the bond. In this kind of bond, rowlocks are laid centered on shiners and every alternate course is vertically aligned. All of the specimens were water cured in a jute bag at a temperature of 25 °C. All the specimens were water cured with the help of jute bag at temperature 25 °C. The average size of the prisms for the compressive strength test was 15.75” × 9” × 24” and the height to thickness ratio was 2.70. Proper capping was done in accordance with practice C1552 before placing the prisms in UTM. The load was applied on specimens at the uniform rate of AAA as shown in Fig. 10. The correction factor against h/t of each specimen was calculated by linear interpolation between the values given in ASTM C1314. A diagonal tension test was conducted on the remaining 36 prisms at the ages of 28 and 56 days using UTM with an average size of 28.5” × 28.5” × 9”. The specimens were placed on the machine in a centered and plumb position.

Fig. 10Diagonal test Sample arrangement in process

Fig. 11Vertical alignment being tested

3.3. Triplet tests for shear strength

A triplet test was performed on the specimens from all brick sources with the purpose of determining the shear bond strength of bed joints in masonry. The test was performed with and without lateral pre-compression load under the specifications of EN 1052-3:2002 [42]. According to the code, three bricks are bonded together with 10 mm mortar. All the specimens were subjected to water curing for 28 days. Before applying load, the end units of each specimen was supported with a 12 mm thick piece of steel to ensure good contact. A total of 15 specimens with uniform representation from all brick sources were tested without pre-compression load under UTM as shown in Fig. 12 and 13. The shear strength of specimens is calculated from the following Eq. (2), Shear strength $f_{voi}$, applied load $F_{imax}$, $A$, area of specimens:

whereas, as shown in Fig. 10, 15 specimens from each brick source were tested with lateral pre-compression loads of 0.2, 0.6, and 1.0 MPa under the same machine. Shear strength for lateral pre-compressed specimens was calculated after finding the pre-compressive load from the abovementioned equation 3. Pre-compressive $f_{pi}$, applied load $F_{pi}$, $A$, area of specimens:

Fig. 12Pressure application on Triplet test sample

Fig. 13Triplet testing arrangement and load application

4.1. Compressive strength test

As per the brick layout pattern, the mean contact area between bricks is 738 in² in a 3288 in³ volume of rat-trap bond prism depicting the contact area to volume ratio as 0.22. The mean brick contact area in the English bond is 43 % greater in 23 % less volume than that of rat-trap bond. The average contact area is 1296 in² in a 2677 in³ prism of English bond, illustrating contact area to volume ratio of 0.48. The comparison of both bonds, with a slightly difference in volumes due to the bricks’ orientation and layout, evidently describes t-effectiveness owing to the lesser utilization of materials and labor in the rat-trap bond.

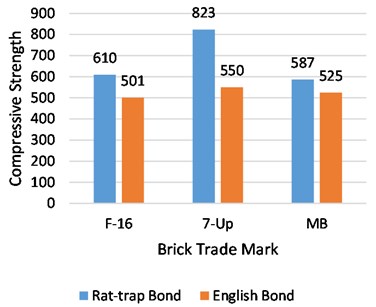
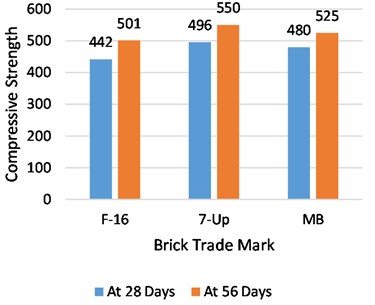
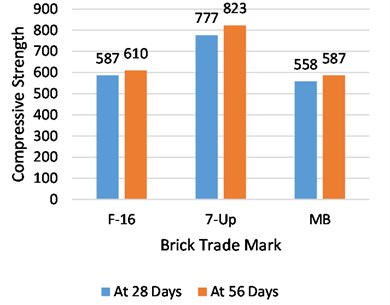
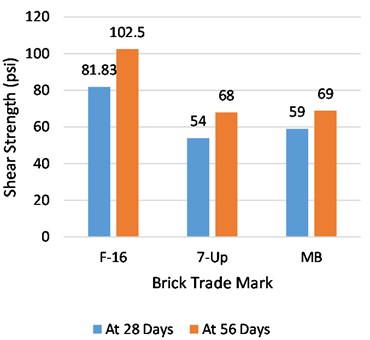
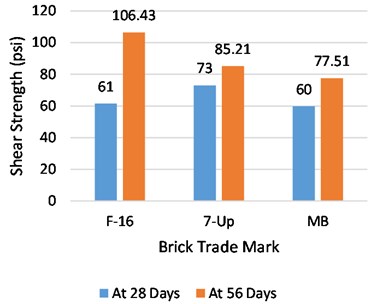
Rat-trap and English bond prisms were tested against compressive strength loads at the ages of 28 and 56 days. From the extensive experimentation, comprising six specimens from each brick source for every test, a tremendous difference was observed between the compressive strengths of both bonds at all ages. At 28 and 56 days, the compressive strength of the F-16 trademark rat-trap bond was found to be 25 % and 18 % higher than that of the English bond, respectively. Similarly, the strength of the rat-trap bond from 7-up bricks was 40 % and 29 % greater than that of other bonds at 28 and 56 days, respectively. In the same way, 14 % and 11 % larger strengths were found in Rat-trap bond prisms than in English bond at the age of 28 and 56 days respectively. The strength gained after 28 days of water curing was very slow in the rat-trap bond and did not put much difference in ultimate strength at the age of 56 days. The strength increase in the rat-trap prisms with F-16, 7-Up, and MB bricks was only 4 %, 6 %, and 5 %, respectively. Whereas English bond prisms showed a greater difference in strength gain after 28 days’ water curing than the other bonds. The strength rises in this type of bond with F-16, 7-Up and MB bricks was observed 13 %, 11 % and 9 % respectively. The leading reason for the higher rate of strength increase in English bond after 28 days is probably the utilization of a larger quantum of mortar in greater contact areas between bricks, which gets more strength with further water curing. A graphical comparison between average compressive strength at the ages of 28 and 56 days and strength increase after 28 days for both types of bonds is drawn in Fig. 14.

The failure of bricks was observed in most of the English bond specimens when subjected to a compressive strength load. Whereas the failure behavior of rat-trap bond prisms was totally different. Due to less contact area between bricks and different bricks layout, most of the failure occurred in mortar rather than bricks in rat-trap specimens.

4.2. Diagonal tension test

Similar to the attributes of prisms for compressive strength, the brick contact area to prism volume ratio for both kinds of bonds differs considerably. The mean brick contact area in the 7179 in 3 volume of Rat-trap bond is 1548 in 2 portraying the contact area to prism volume ratio of 0.21. The contact area in this kind of bond is 120 % less in only 5.4 % greater volume than that of an English bond, in which the mean contact area in 6788 in 3 volume of prism is 3402 in 2 representing a contact area to volume ratio of 0.50. Although, the sizes of specimens prepared for compressive strength and diagonal tension tests are different, the contact area to prism volume ratios are almost the same. From the geometry evaluation of prisms, much less material is used in the rat-trap bond as compared to the conventional bond, making it more economical.

Fig. 14Average compressive strength of English and rat-trap bond at the age of 28 and 56 days

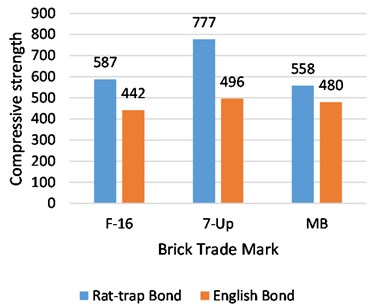
a) Compressive strength at 28 days

b) Compressive strength at 56 days

c) Compressive strength of English bond

d) Compressive strength of Rat-trap Bond

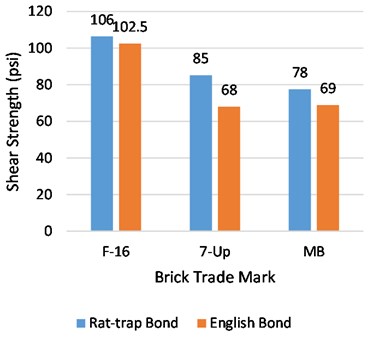
18 specimens were tested against a diagonal tension test for each type of bond at a single age with six specimens from each brick source. There was found to be a considerable difference in the shear strength of both kinds of bonds at the ages of 28 and 56 days. For brick trademark F-16, the shear strength of rat-trap was observed to be 33 % less than that of English bond at the age of 28 days, whereas it showed a 4 % greater value of strength than that of English bond at the age of 56 days. On the other hand, rat-trap prisms made from bricks 7-Up and MB resulted in 26 % and 8 % at the age of 28 days and 20 % and 11 % at the age of 56 days respectively. The increment pattern in strength due to additional water curing after 28 days to 56 days, was not found to be very smooth for both types of bonds. The shear strength increment in Rat-trap bond prisms with F-16, 7-Up and MB bricks was 73 %, 17 %, and 30%, respectively. English bond, on the other hand, produced nearly identical shear strengths for F-16, 7-Up, and MB brick specimens, namely 25 %, 26 %, and 17 %, respectively. A graphical comparison between average shear strength at the ages of 28 and 56 days and strength increment after 28 days for both types of bonds is drawn in Fig. 15.

The failure of bricks was observed in most of the English bond specimens when subjected to diagonal tension load. Whereas, the failure behavior of rat-trap bond prisms was totally different. Due to less contact area between brick layouts and different bricks layout, most of the failure occurred in mortar rather than bricks in rat-trap specimens.

Fig. 15Average shear strength of English and Rat-trap bond at the age of 28 and 56 days

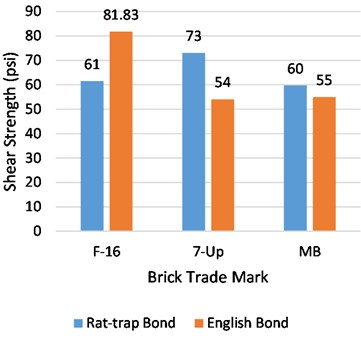
a) Shear strength at 28 days

b) Shear strength at 56 days

c) Shear strength of English bond

d) Shear strength of Rat-trap bond

4.3. Triplet test for shear bond strength

Two types of loading arrangements were made for the triplet test of prisms. One arrangement was without lateral pre-compression load, for which 18 prisms with six specimens from each brick source were tested. The average shear bond strength for prisms made of the F-16, 7-Up and MB bricks was 22.56 psi, 31.40 psi, and 30.79 psi, respectively, with an overall mean value of 26.46 psi. For one prism of F-16 brick trademark, shear strength obtained at 78.99 psi was ignored due to being an outlier. The characteristic shear strength based on the mean value is calculated as 21.17 psi, whereas the same strength based on the lowest value is obtained as 11.50 psi. Fig. 16 shows the graphical presentation of the average shear strength of all brick sources.

The second arrangement was made by applying 29 psi, 87 psi, and 145 psi, lateral pre-compression loads, with each set of loads for five specimens from every brick source. For F-16 brick prism, the shear strengths obtained against 29 psi, 87 psi and 145 psi lateral pre-compression loads are 27.73 psi, 68.62 psi, and 121.92 psi, respectively. The strength of 76.02 psi obtained for a specimen subjected to 87 psi lateral load, was ignored due to unit splitting failure occurrence. The shear strengths determined against 29 psi, 87 psi, and 145 psi lateral load for the 7-Up brick prism are 68.80 psi, 91.89 psi, and 96.29 psi, respectively. For this also, two values of strengths, 147.76 psi, and 87.91 psi, were ignored because of unit splitting failure. However, for MB brick specimens, the shear strengths found against 29 psi, 87 psi and 145 psi lateral load are 50.25 psi, 69.84 psi, and 90.33 psi, respectively. For this series of tests, the values of strengths of 34.02 psi and 38.40 psi were ignored owing to unit splitting failure. Linear regression analyses between shear strength and lateral pre-compressive strength for all kinds of bricks prisms are carried out and shown in Fig. 17 and 18.

Fig. 16Average shear bond strength of all brick trade marks without precompression load

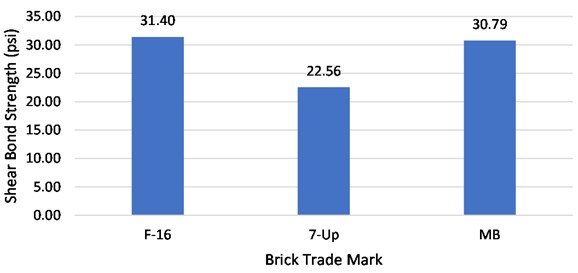
Fig. 17Average shear bond strength of all brick trade marks with precompression load

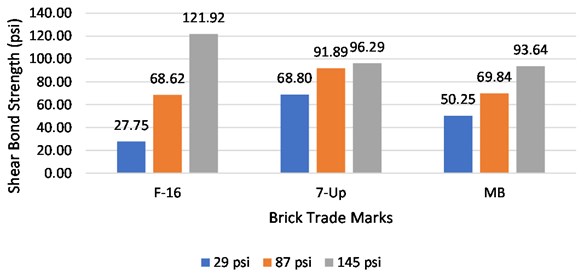
Fig. 18Leading characteristics of shear strength for all types of bricks prisms

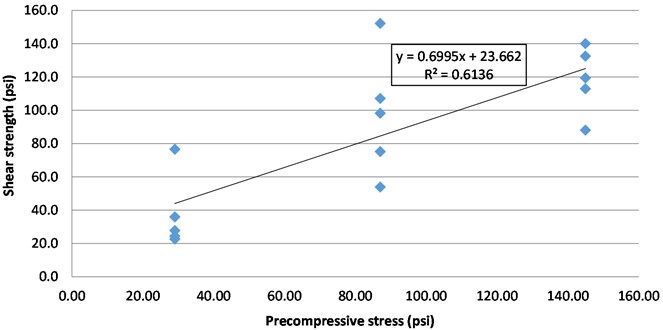
a) Shear strength vs precompressive stress for F-16 Bricks. $f_{vo}$= Mean initial Shear strength (psi) = 21.7; $f_{vok}$ = 0.8×$f_{vo}$= Characteristic initial sh. Strength (psi) = 17.12; Angle of internal friction ($\alpha$) = 0.72; Characteristic angle of internal friction = $\mathrm{t}\mathrm{a}\mathrm{n}\alpha k=0.8\mathrm{t}\mathrm{a}\mathrm{n}\alpha$ = 0.01

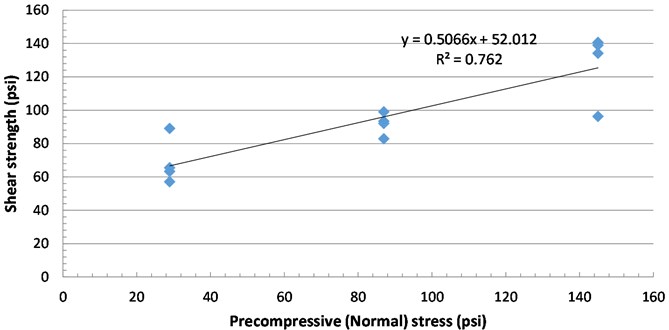
b) Shear strength vs precompressive stress for 7-Up bricks. $f_{vo}$ = Mean initial Shear strength (psi) = 57.16; $f_{vok}$ = 0.8×$f_{vo}$ = Characteristic initial sh. Strength (psi) = 45.73; Angle of internal friction ($\alpha$) = 0.4; Characteristic angle of internal friction = $\mathrm{t}\mathrm{a}\mathrm{n}\alpha k=0.8\mathrm{t}\mathrm{a}\mathrm{n}\alpha$ = 0.006

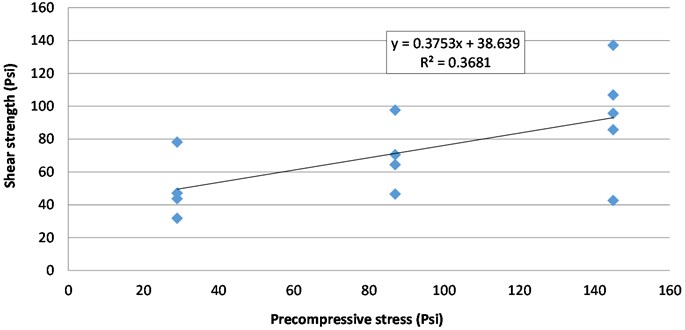
c) Shear strength vs precompressive stress for MB-Bricks. $f_{vo}$ = Mean initial Shear strength (psi) = 40.07; $f_{vok}$= 0.8×$f_{vo}$ = Characteristic initial sh. Strength (psi) = 32.06; Angle of internal friction ($\alpha$) = 0.345; Characteristic angle of internal friction = $\mathrm{t}\mathrm{a}\mathrm{n}\alpha k=0.8\mathrm{t}\mathrm{a}\mathrm{n}\alpha$ = 0.005