Relationship of rock microscopic parameters with the elastic modulus and strength

3.1. Effect of microscopic parameters on the elastic modulus

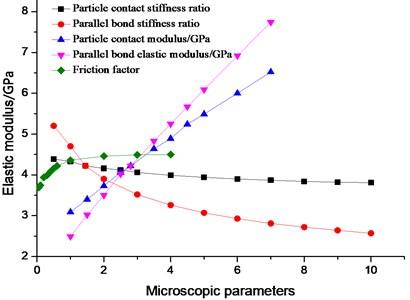
Through numerical simulation test and control variable method, different microscopic parameters were varied to obtain different macroscopic elastic moduli. The influence of the change of microscopic parameters on the elastic modulus $E$ of the simulated specimens is shown in Fig. 2.

The influence of the particle contact modulus $E_C$ and the elastic modulus of the parallel bond $\overline{E_c}$ on the elastic modulus of the specimen was the most significant and most linear. The effect of the elastic modulus of the parallel bond was the greatest, whereas that of the particle contact stiffness ratio $k_n$/$k_s$ was the lowest. Under constant parameters, the elastic modulus $E$ of the specimen increased with enlarging elastic modulus of the parallel bond $\overline{E_c}$, particle contact modulus $E_C$, and friction factor $\mu$. The elastic modulus of the specimen decreased with the particle contact stiffness ratio $k_n$/$k_s$ and the parallel bonding stiffness $\overline{k_n}/\overline{k_s}$. The effect of the parallel bond stiffness ratio $\overline{k_n}/\overline{k_s}$ and friction factor $\mu$ was relatively large at some stage. The stage for the $\overline{k_n}/\overline{k_s}$ was about 0.5-4 and 0.1 ≤ $\mu$ ≤ 1. In accordance with the order of influencing factors, the parameters affecting the elastic modulus E of the specimen are parallel bond elastic modulus $\overline{E_c}$, particle contact modulus $E_C$, and parallel bond stiffness ratio $\overline{k_n}/\overline{k_s}$. The influence factor of the elastic modulus of parallel bond $\overline{E_c}$ on the elastic modulus $E$ was greater than that of the particle contact modulus $E_C$. With rising parallel bond stiffness ratio $\overline{k_n}/\overline{k_s}$, the “rigidity” of the specimen gradually increased, and the “elasticity” gradually diminished, that is, the macro elastic modulus E decreased. On the basis of linear and nonlinear fitting, the relation of $\overline{E_c}$, $E_C$, and $\overline{k_n}/\overline{k_s}$ with the elastic modulus $E$ is as follows:

Fig. 2Influence of microscopic parameters on elastic modulus

3.2. Influence of microscopic parameters on Poisson’s ratio

We used the discrete element numerical simulation test to prepare the Poisson’s ratio of the specimen. The influence of the variation of each parameter on the sample’s Poisson’s ratio was compared (Fig. 3).

Fig. 3The influence of microscopic parameters on Poisson’s ratio

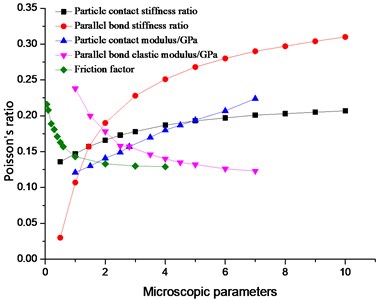
The Poisson’s ratio of the specimen was most influenced by the parallel bond stiffness ratio $\overline{k_n}/\overline{k_s}$, and their relation was nonlinear. The Poisson’s ratio of the specimen rose with increasing parallel bond stiffness ratio. This is result was achieved because the parallel bond stiffness incrementally exceeded the shear stiffness; the number of normal cracks in the specimen was greater than that of the tangential crack. On the macro level, the transverse strain gradually enlarged, and the axial strain gradually reduced; as a result, the Poisson’s ratio rose. The particle contact modulus EC, parallel bond elastic modulus, and friction factor all influenced the Poisson’s ratio, but the effect was less than that of the parallel bond stiffness. The relation between the particle contact modulus (EC) and the Poisson’s ratio was linear. The properties of the specimen remained unchanged, and with the rising particle contact modulus EC, the overall performance and strength of the specimen were enhanced. Therefore, the Poisson’ ratio was augmented because of the parallel bond stiffness ratio $\overline{k_n}/\overline{k_s}$, and the contact modulus EC was altered. With rising $\overline{k_n}/\overline{k_s}$, the properties of the specimen changed, but the increased EC only improved the overall specimen performance. The influence of parallel bond modulus and friction factor on the Poisson’s ratio was negatively correlated. Similar to their influence on elastic modulus, the two factors were extremely influential at a certain stage. The elastic modulus of the parallel bond was approximately 1-4 GPa, and the friction factor was in the 0.1-1 stage. When the parallel bond elastic modulus $\overline{E_c}$ > 4 GPa, the friction factor $\mu$ > 1, the change in Poisson’s ratio of the specimen was relatively slow. Fig. 3 reveals that the particle contact stiffness was less than $k_n/k_s$. However, with the rise in particle contact stiffness ratio of $k_n/k_s$, the Poisson’s ratio of the specimens gradually enlarged. This result was achieved because the axial strain diminished, and the Poisson’s ratio of the specimen gradually increased. The analysis showed that the factors that exerted the greatest impact on the specimens’ Poisson’s ratio (on the basis of impact factor order) are the parallel bond stiffness ratio $\overline{k_n}/\overline{k_s}$, parallel bond elastic modulus, and particle contact modulus EC. Given the fitting, the effects of $\overline{k_n}/\overline{k_s}$, $\overline{E_c}$, and $E_C$ to the Poisson’s ratio are as follows:

3.3. Influence of microscopic characteristic parameters on the uniaxial compressive strength

The effects of the microscopic parameters on the uniaxial compressive strength of uniaxial compressors were compared (Fig. 4). The effect of particle contact stiffness ratio of $k_n$/$k_s$, parallel bond stiffness ratio $\overline{k_n}$/$\overline{k_s}$, and particle contact modulus EC on the uniaxial compressive strength was less than that of the particle friction factor $\mu$. The effect of $\overline{k_n}$/$\overline{k_s}$on the uniaxial compressive strength was slightly smaller than that of the friction factor. The variation range of uniaxial compressive strength was 9.55 MPa and decreased with increasing $\overline{E_c}$. When $k_n$/$k_s=$ 1, the uniaxial compressive strength obtained its maximum value of 28.48 MPa and decreased with increasing $k_n$/$k_s=$ 1. When the parallel bond stiffness ratio $\overline{k_n}$/$\overline{k_s}=$ 2, the uniaxial compressive strength achieved its maximum value of 28 MPa. When 0 < $\overline{k_n}$/$\overline{k_s}$ ≤ 2, the uniaxial compressive strength increased with $\overline{k_n}$/$\overline{k_s}$. However, when $\overline{k_n}$/$\overline{k_s}$ > 2, the uniaxial compressive strength was negatively correlated.

Fig. 4Influence of the microscopic parameters on uniaxial compressive strength

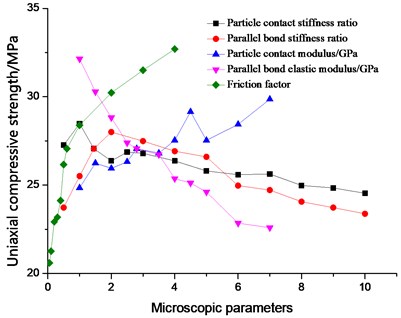
As shown in Fig. 4, the uniaxial compressive strength was positively correlated with the particle contact modulus EC but negatively correlated with the parallel bond elastic modulus, which was due to the parallel bonding model used in this paper. $\overline{E_c}$ determines the nature of the specimen to a certain extent, and as the parameter’s value increases, the “rigidity” of the simulation specimen is simulated, and the mode of destruction becomes brittle failure. The increase in EC raises the compressive strength of the specimen, that is, the uniaxial compressive strength increases with enlarging EC. In these five microscopic parameters, $\mu$ exerted the most major influence on uniaxial compressive strength. With increasing $\mu$ between particles, the bite force between particles enlarges, and the peak strength of the material rises. Given the fitting, the effects of $\mu$ on the uniaxial compressive strength are as follows:

3.4. Effect of parallel bond strength on uniaxial compressive strength

The effects of the parallel normal bond strength and tangential bond strength on the uniaxial compressive strength were analyzed. The corresponding average bond strength ratio was 0.1-3.0 when the $\sigma$ was 2-60 MPa. Meanwhile, the corresponding average bond strength ratio was 0.1-4.0 when the $\tau$ was 5-200 MPa. The influence of average bond strength on the macroscopic mechanical properties of specimens (Tables 3 and 4) and the parameter’s effect on uniaxial compression strength is shown in Fig. 5.

Fig. 5Relation between bond strength ratio and uniaxial compressive strength

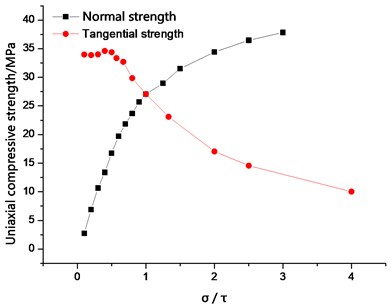
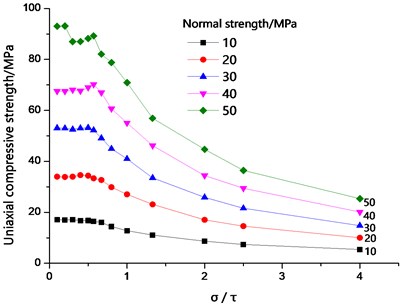
Tables 3 and 4 indicate that the average normal bond strength and the tangential bond strength only slightly affect the Poisson’s ratio. However, between the two factors, the average bond strength exerts a greater influence than on the uniaxial compression strength (Fig. 5). At 0 < $\sigma$/$\tau$ ≤ 0.67, the variation of the uniaxial compressive strength was large and exponential with the increase in average normal bond strength. The average tangential bond strength exerts no effect on the uniaxial compressive strength. This result was achieved because when the average tangential bond strength was greater than the normal bond strength, the main factor of the failure of the specimen was the normal bond strength, and the ultimate failure mode was tensile failure (Fig. 6). When the average tangential bond strength was less than the normal bond strength, the specimen achieved a small amount of tangential crack, but mainly, normal failure. When $\sigma$/$\tau$ > 0.67, the sample was mainly affected by the average tangential bond strength, and when the average normal bond strength increased, the specimen was transformed from brittle deformation to plastic deformation, and the failure mode changes to the shear failure mode (FIG. 7). The crack initiation was gradually increased, and the quantity was greater than the number of normal cracks. The average normal bond strength (10-50 MPa) and average tangential bond strength (10-50 MPa) were changed, and the relationship between bond strength ratio and peak strength was analyzed (Fig. 8). The average bond strength ratio was set to 0.1-4, and the average normal bond strength was assigned to 10-40 MPa. When the average bond strength ratio was 0 < $\sigma$/$\tau$ ≤ 0.67, the uniaxial compressive strength was mainly affected by the average normal bond strength. When the average bond strength ratio was $\sigma$/$\tau$ > 0.67, the uniaxial compressive strength decreased with decreasing average tangential bonding strength. As the average bond strength between particles rose, the effect of the average tangential bond strength on the uniaxial compressive strength also increased.

Fig. 6Uniaxial compression failure crack (mainly normal failure)

Fig. 7Uniaxial compression failure crack (mainly tangential failure)

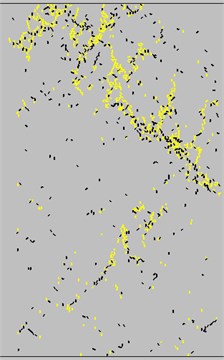
Fig. 8Relationship between bond strength ratio and peak strength with different normal bond strength

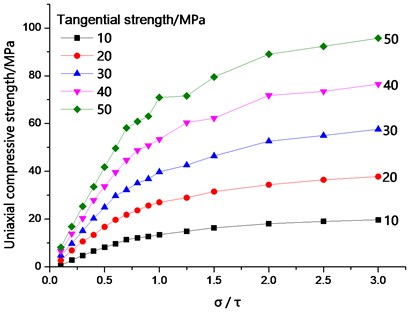
The relationship between bond strength ratio and peak strength of different tangential bond strengths was analyzed (Fig. 9). The average bond strength ratio was set to 0.1-3.0. When the average bond strength ratio was 0 < $\sigma$/$\tau$ ≤ 1.0, the uniaxial compressive strength increased with increasing average normal bond strength. The average normal bond strength augmented with rising average tangential bond strength. At the same time, the total bond strength of the particles increased, and the uniaxial compressive strength of the specimen increased. When 0 < $\sigma$/$\tau$ ≤ 1.0, as the bonding strength between particles enlarged, the effect of the average normal bond strength on the uniaxial compressive strength also intensified. When $\sigma$/$\tau$ > 1, the uniaxial compressive strength was mainly affected by the average tangential bond strength.

Fig. 9The relationship between bond strength ratio and peak strength for different tangential bonding strength