Experimental diagnosis of multiple faults on a rotor-stator system by fast Fourier transform and wavelet scalogram

2.1. A brief background of continuous wavelet transform (CWT)

In order to describe qualitatively the oscillated feature of nonlinear and transient systems, an algorithm called wavelet transform (WT) technique is explained briefly in this section. WT offers a variable window technology that uses a time adaptive interval to analyse high and low frequency components of a signal.

In this paper, WT offers flexibility to describe experimental test signals that comprise time-variant frequencies.

Given a signal $f\left(t\right)$, the associated (CWT) is represented by:

where $a$ and $b$ are the scale parameter and time translation factor respectively. The term ${\psi }_{a,b}^{\mathrm{*}}\left(\omega \right)$ denotes the complex conjugate of ${\psi }_{a,b}$, which are the daughter wavelets (i.e. the dilated and shifted versions of the ‘mother’ wavelet $\psi \left(t\right)$, which is continuous in time and frequency). It is worthwhile to note that when perfect reconstruction is required, the selection of the mother wavelet $\psi \left(t\right)$ becomes restricted. In general, the function $\psi \left(t\right)$ has to be such that:

where $\psi \left(\omega \right)$ is the FFT of $\psi \left(t\right)$ for a successful inverse transform, admissibility condition, implying that $\psi \left(0\right)=$ 0, $0<C_{\psi }<+\mathrm{\infty }$, has to be fulfilled. Once $\psi \left(t\right)$ meets this condition, $CWT(a,b)$ can be adopted as a weighting function to synthesise the original signal $f\left(t\right)$ from the dilated and translated versions of $\psi \left(t\right)$ as follows [8]:

The representation of $f\left(t\right)$ in terms of CW is redundant because it continuously varies the scaling parameter $a$. The original signal can be completely reconstructed by a sampled version of $CWT(a,b)$ as in [14]. Among the multiple types of wavelet families developed, the Morlet mother wavelet is quite well localised in time and frequency space and has been adopted in this paper. Morlet mother wavelet is defined in time domain by Eq. (3):

where $m$ is the wave number and $\tau$ is non-dimensional time parameter. Eq. (4) indicates the CWT of a signal $f\left(t\right)$ can work as a band-pass filter with the wavelet function itself and its scale parameter controls the filtering performance.

2.2. Experiment set-up of Bently RK-4 rotor kit

To analyse vibration signals and validate the effectiveness of the applying CWT method, an experiment is conducted on a RK-4 rotor test rig. A large number of tests on faulty and unfaulty rotor systems operating at variable motor speeds have been done. Fig. 1 shows an overall view of the experimental and the signal acquisition system. The rig consists of an elastic steel shaft coupled to a motor speed control and supported by two bearings. The shaft carries one rigid disc at the mid-span. The rotor shaft was supported on two roller bearings at both ends and sustained in position by two fixed steel supports (designated as supports A and B in Fig. 1(b)). Experimental test data were obtained using the RK-4 vibration test rig in healthy and faulty conditions. Two identical and perpendicular proximity probes mounted from the vertical and oriented in two planes perpendicular to the shaft, captured the relative deflection of the shaft.

Fig. 1A photo of the RK-4 experimental system: 1 – ascent; 2 – scout 100; 3 – data acquisition; 4 –motor; 5 – probes; 6 – shaft; 7 – crack simulator; 8 – disc; 9 – shaft support; 10 – tachometer; 11 – screw rub-contact

a)

b)

The rig, which was integrated with a crack simulator, comprised of two radial and orthogonal springs to emulate dynamics of breathing crack. An extra mass and a screw were used in practice to induce unbalance and to understand the nonlinear dynamics of coupling faults of crack and rub-impact in an RK-4 system.

Rub impact was set at a point located by a number 11 (Fig. 1(b)), which consists of a detachable small tight screw at a controlled distance between the rotor and the screw. The proximity probes recorded regular slightest contacts occurring during the rotation of the shaft. Motor speed control was set to ensure that the rotor was driven only in one direction to avoid reversal of the friction forces induced by rub. The Ascent signal amplifier was used in the data acquisition interface system controlled by Ascent via Matlab toolbox. The shaft’s speed was monitored by a laser tachometer that was mounted on the support.

The signals were recorded in radial direction at various rotating speeds by four proximity probes staggered in the probe block as shown in Fig. 1(b). The sensors were positioned at distances enough to measure rotor shaft vibration in various positions. All the outputs were displayed on an oscilloscope integrated with a filter. A torsional elasticity of the shaft is considered by the assumption that the torque or axial force is applied to twist the rotor torsionally. For all the experiments conducted in this study, a Commtest instrument version 11.6.0 combined with an Ascent 2013 that linked with a data acquisition interface unit was used for data acquisition (Fig. 1(a)). The signals were analysed using Scout 100 and Vibration Assistant software. The acquired data were recorded and then transferred to the computer for digital processing using FFT and CWT. Table 1 gives the physical parameters of the RK-4 rig.

3.1. Dynamic vibration response of rotor with unbalance and axial force

In this first experiment, the torsional deflections were considered by varying the motor input torque. Subsequently, a joint examination of frequency spectrum, rotor trajectory, orbit patterns and CWT enabled the features of unbalance to be identified from experimental vibration test data. Unbalanced rotor responses at a high speed of up to 10.000 rpm were obtained manually by changing the motor’s speed (Fig. 1). Figs. 2 and 3 illustrate the obtained results.

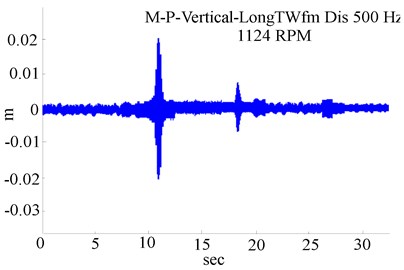
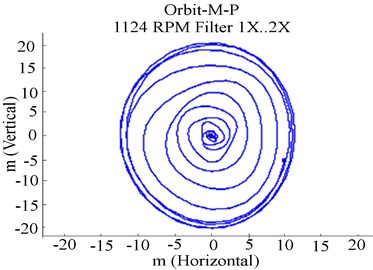
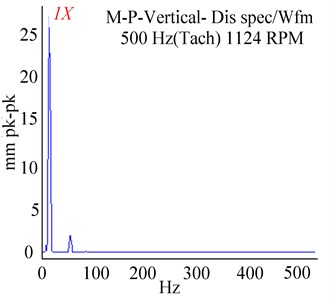
Response to unbalance in the absence of a crack and rub is shown in Figs. 2 and 3. Analysis of the orbit patterns presented in Fig. 2(b) reveals that the unbalance was a source of extra evolutions in the dynamic response, as rotor passed through its critical speed. It was observed in Fig. 2(b) that unbalance induced a regular orbit pattern containing a circular loop. As illustrated in Fig. 2(b), the orbit response initially varied from the start-up to a maximum amplitude $R_1=$ 23.3 mm at resonance and ceded to a regular circular closed loop. The orbit amplitude is found to be $R_2=$ 2.3×10^-6 m in Fig. 2(b), where the first critical speed range is specifically $\omega 1=$ 1132.27 rpm in Fig. 2(a). In Fig. 2(c), the amplitudes of the experimental frequency data revealed that the order 1X harmonic representing the higher vibration level was attained at 23.46 Hz. A correlation between the results in [9] and experimental results in the current paper can be perceived in deflection shapes, frequencies and orbits.

Further experimental investigation on unbalance at low and high speeds of 1150 rpm and 2570 rpm, sampled at 500 Hz was done using CWT. This was done in order to investigate further hidden information from the measured data. The choice of an appropriate wavelet was important for this signal analysis. Daubechies wavelet and the Morlet wavelet were adopted for diagnosis of unbalance. Experimental responses in terms of 2-D and 3-D scalograms are presented in Figs. 3 and 4. In Figs. 3 and 4, the 2-D and 3-D CWT response scalogram of an unbalanced rotor were smooth except at one point. The figure depicts a slight fluctuation and resonance at $t=$ 3400 s due to eccentric mass elements. In 3-D of Fig. 3(b), at rotor speed of 1124 rpm, the unbalance mass caused excitation that is shown by a high concentration of energy (red colour) after the first resonance.

Fig. 2Start-up response of rotor system with unbalance at 1124 rpm: a) lateral shaft deflection, b) unbalanced orbit response, c) experimental FFT spectrum

a)

b)

c)

Fig. 3Experimental 2-D and 3-D response scalograms by CWT for unbalanced RK-4 at 1124 rpm: a) lateral shaft deflection, b) 3-D CWT of lateral unbalanced rotor

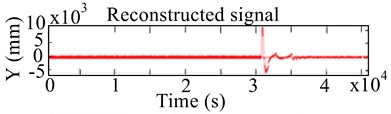
a)

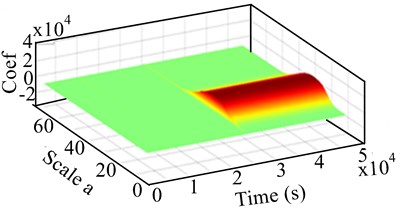
b)

Increasing the rotor speed to 2570 rpm generated a slight change in frequencies as indicated in 3-D of Fig. 4(b). In Fig. 4(b), filtering the frequency range from 80 to 237 Hz revealed the existence of more than one mode (a rather dense red zone), with high precision on the existence of some buried frequencies not visible in the FFT spectrum. Examination of the Fig. 4(b) revealed that numerous small resonance peaks with lowest order frequencies appeared in the 3-D scalogram at varying periods of time. Such peaks were completely indiscernible in the experimental signal in Fig. 2(c). As seen in the CWT in Fig. 4(b), unbalance at a high speed of 2570 rpm caused a significant disturbance in the RK-4 system, which was manifested by numerous small buried frequency peaks.

Analysis confirms that unbalance in the rotor system led to significant energy fluctuations. Thus, it is clear that the fluctuations in rotor system time waveform curves became obvious in CWT and revealed multiple small changes in frequency with respect to the rotor speed. This ascertains that high speed excites high vibration, unbalance and nonlinear forces in the system.

Fig. 4Experimental 2-D and 3-D CWT response scalogram of unbalanced RK-4 at 2570 rpm: a) lateral unbalanced shaft deflection, b) 3-D CWT of lateral deflection of unbalanced rotor

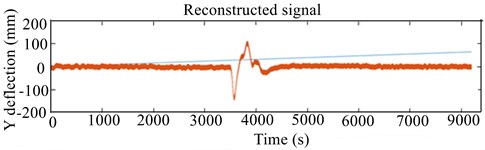
a)

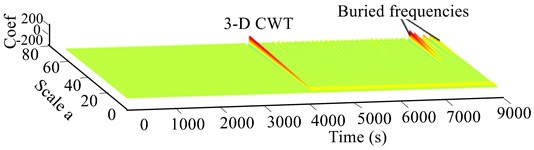
b)

3.2. Experimental vibration response of rotor with unbalance and rotor-stator rub

Evolution of this phenomenon has been investigated in this section following the same process of experimentation as in the previous section. Subsequently, for this purpose, the results of CWT applied to experimental test data of unbalanced rotor with rub are presented and discussed in the following section.

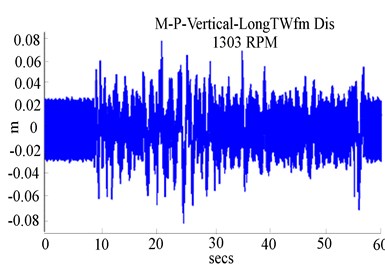
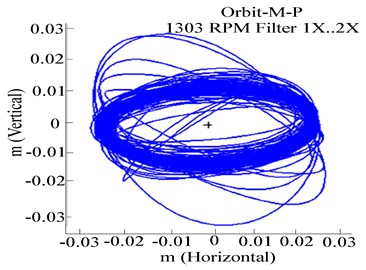
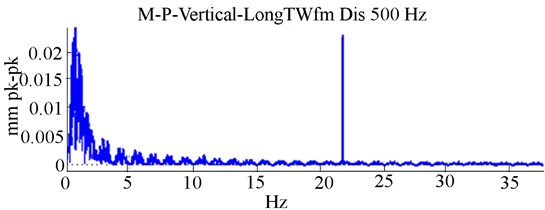
Fig. 5Experimental response of RK-4 at 1303 rpm, with rub-impact: a) Y-deflection, b) orbit patterns, c) frequency response

a)

b)

c)

The reduction of clearance generated not only a high rub-impact but also the existence of remarkable disparities in sub-resonances, which exhibits higher amplitudes in the lateral deflection under rub, where the first critical speed is observed at $t=$ 12 s as illustrated in Fig. 5(a). Experimentally it was noted that rotor-stator rub increased the rotor critical speed. It is clearly shown rub-impact amplitude levels depend significantly on the rotor speed, which increased the rotor critical speed from $\omega 1=$ 1124.43 rpm in Fig. 2(a) to $\omega 2=$ 1300.43 rpm in Fig. 5(a) when the rotor is accelerated.

The experimental orbit patterns in Fig. 5(b) show a complex shape illustrating the multiple rotor-stator rebounds at impact points. A significant distortion in orbits due to rub in the system was obvious. In Fig. 5(b), the inside circular-loop orbit observed for a case of unbalance was significantly modified to an outside elliptic shaped orbit due to rub. The FFT in Fig. 5(c) indicates an increased amplitude of 1X harmonic components representing the higher vibration level as previously observed in Fig. 2(c) and disturbed sub-harmonic peaks. It should be noted that the tightening of 1/2X frequency peaks (sub-harmonics) in Fig. 5(c) was due to the presence of rub. In Fig. 5(c), the main peak coincided with the main rotor frequency at 22.5 Hz. The gap between two consecutive peaks was found to be in the range of 22.5 Hz, which was the unbalanced shaft’s rotational frequency.

By observing the peaks, evolution of energy associated with a fault could be traced. Consistently, it was concluded that the number and the level of the various peaks observed in the FFT depend on the severity of rub-impact. Distinguishing unbalance from rub can be done based on the size of the irregular and disorganised loops, the abrupt change in transient frequency response and the variation in deflection waveform as the rotor traverses the first critical speed. Furthermore, the assigned rub signature has been experimentally used in the CW analysis to obtain the wavelet coefficients and to detect the occurrence of rub. Fig. 6 shows the scalogram of the vibration signals of the unbalanced rotor-stator with rub conditions in time-frequency domains.

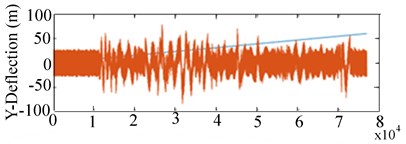
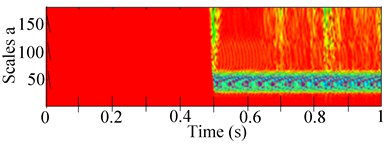
Fig. 6Experimental 2-D and 3-D of CWT and scalogram response of the RK-4 with unbalance and rub at 1303 rpm: a) lateral unbalanced shaft deflection with rub, b) corresponding 2-D CWT (c) 3-D CWT scalogram

a)

b)

c)

In 2-D of Figs. 6(b) and 6(c), the values of wavelet coefficients obtained during rotor-stator rub indicate high amplitude peaks when the rotation speed approaches the first critical frequency. The evolution with respect to wavelet coefficients was observed and drawn respectively at particular scales s of 10 and 50. Examining the respective scales, it became apparent that energy due to rotor-stator rub was mainly concentrated around the frequency intervals, 7-13 Hz at 1303 rpm followed by 27-81 Hz at 2216 rpm. The energy dissipated at the highest speed of 2216 rpm was obviously higher than the energy dissipated at 1303 rpm.

The concentration of energy emitted at the start-up of each signal indicated the existence of various frequency resonances but at different intervals of time as seen in 2-D Fig. 6(b) and 2-D Fig. 7(a). Indeed, in Figs. 6 and 7, when the speed of the shaft varied between the time ranges 2 to 14 seconds, various regularly spaced frequency lines asymmetric with the source frequency appeared in the distribution. In addition, the lines varied nonlinearly with time and were proportional to the shaft rotational frequency with a different proportionality factor from one line to another. At high speed operation, rub imparts an important component in the scalogram response. It was apparent that rub modulated the harmonic peaks at the critical shaft frequencies as shown in 3D CWT Fig. 7(b). The redundant largest peaks of the distribution were attained at 500 Hz (second harmonic of the maximum rotational frequency) observed at the end of the acceleration phase (after approximately 5000 seconds). This revealed that the observed phenomenon is strongly modulated by the rotor speed and that the signal is aperiodic. However, from the difference in the spectrum in Figs. 6 and 7, it was possible to identify the defect manifested by the signal.

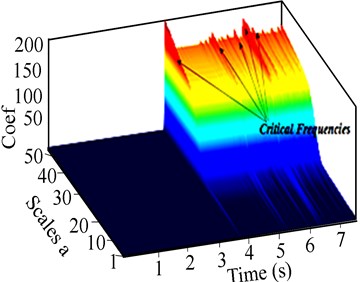
Fig. 7Experimental 2-D and 3-D CWT response of the RK-4 with unbalance and rub at 2216 rpm: a) lateral shaft deflection, b) corresponding 2-D CWT (c) 3-D CWT scalogram

a)

b)

In 3-D of Fig. 7(b), continuous bright fringes indicative of rub as a primary source of excitation in the vibrating system were evident. The scalogram produced at the rotational speed of 2216 rpm in 3-D of Fig. 7(b) was rich in peaks of relatively high amplitudes. These peaks, which are due to contact and unbalance, were observed in the scalogram, probably because of the high rotational speed (2216 rpm). The first harmonic occurring at $t=$ 5000 s could not be easily discerned due to recurrent rub-impact in 3-D of Fig. 7(b). Rub was noted before and after the first resonance by tracing the number of resonance peaks in FFT, in Fig. 5(c) and CWT in 3-D of Fig. 7(b). The 3-D scalograms were illustratively conspicuous; they were adopted to indicate the number of shocks in the sampled signal. The scalogram in 3-D of Fig. 7(c) indicated that the peaks due to rub varied in magnitude and manifested a series of periodic shocks. The results in Figs. 6 and 7 suggest that the degree of rub can effectively be diagnosed with respect to the speed and the rub impact frequency. Therefore, time and scale coefficients of faults in Figs. 6 and 7 were localised based on time-frequency analysis and energy distribution in the 3-D scalogram of the CWT.

3.3. Dynamic vibration response of rotor excited by unbalance and a crack

For the coexisting multi-faults case (i.e., unbalance, crack), performance of the CWT method in faulted signal extraction is experimented for flexible RK-4 shafts. The performed investigations through the orbit, shaft’s deflection and the frequency spectrum are presented in Fig. 8 and further processed by CWT in 2-D and 3-D as shown in Figs. 9 and 10 for more wide analysis.

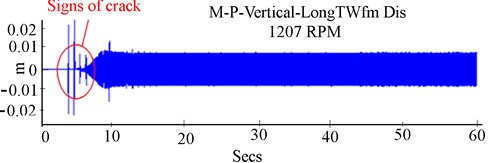
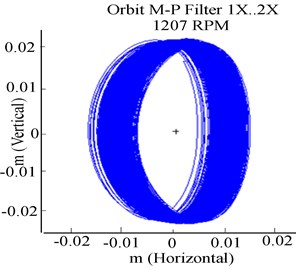
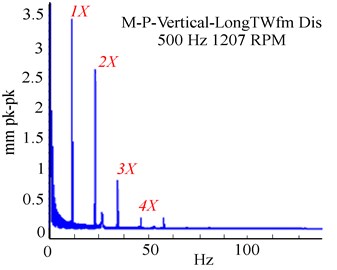
Fig. 8Experimental RK-4 response at 1207 rpm, with unbalance and a crack (ΔKξ/KYY= 0.55): a) Y-deflection, b) experimental orbit, c) frequency response

a)

b)

c)

From the deflection in Fig. 8(a), some irregular and imprecise fluctuation peaks exist in the extracted lateral deflection. The crack features were manifested by small tight peaks at the rotor start-up, unlike the observations in the previous analysis (Fig. 2(a) and 5(a)). In Fig. 8(b), the presence of a crack presented strong tightening loops. A qualitative difference in this case compared to the orbit obtained in Fig. 2(b) is already apparent. In Fig. 8(c), a high vibrational level was attained by order 1X harmonic at 23.46 Hz. At this point, the crack generated a tremendous increase in vibration amplitudes, characterised by the 2X and 3X super harmonic peaks.

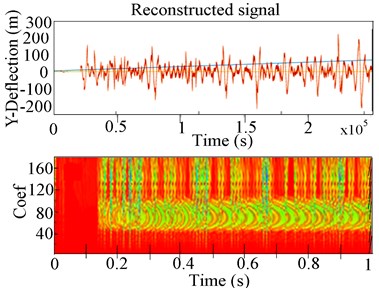
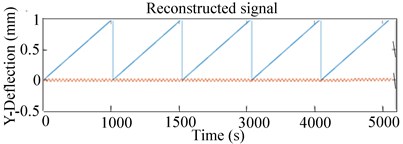
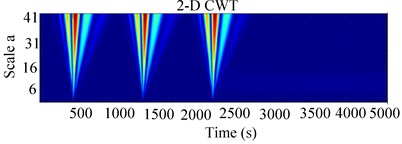
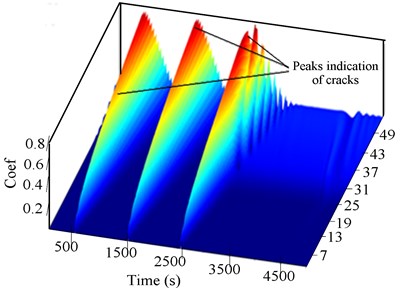
A better resolution was then found to extract features from the multi-faulted data by CWT at a translational frequency of 40 Hz and implemented in Fig. 9 and Fig. 10. In 3-D of CWT shown in Fig. 9(c), a series of peaks, three eigenmodes appeared clearly (respective values 500, 1500 and 2500 s). The peaks of frequencies are excited by breathing of the cracks; an accumulated energy distribution of these peaks can be observed from the higher spectral in Fig. 9(c). The order of the frequency appearance revealed the periodic opening and closing of the crack to be $t=$ 1000 s as illustrated in Figs. 9(a), (b) and 10(c). The period increased as a function of the scale coefficients when the rotor speed increased to 2216 rpm.

The time taken to pass through the critical and sub-critical speeds being more at a low speed of 1207 rpm, the sub-harmonic resonant peaks were clearly seen in the CWT scalogram Fig. 9(a). The higher peak indicators of a crack effect disappear once the rotor recovers its stability as observed in Fig. 9(c). However, as the RK-4 rotor speed increased as shown in Fig. 10(a) and 10 (b), the sub-harmonic peaks in time-response became hidden and considerable features of the crack could only be manifested in the CWT scalogram by accumulated energy distribution observed from the marginal spectral as revealed in Fig. 10.

In Fig. 10, the experimental test data at a high speed depicted the 1X critical speed at 500 s, characterising the effect of unbalance. It can be seen in Fig. 10(a) that the peaks appearance shows regular and precise variations of amplitude in the multi-faulted data, excited by the coexisting unbalance and crack faults. The main harmonic resonant peak was observed in Fig. 10(a), which became conspicuous in the 3-D CWT scalogram in Fig. 10(b). Increasing the speed to 2216 rpm intensified the system vibration, generating the second and third critical speeds (at $t=$ 1500 s and $t=$ 2500 s) as illustrated in the 3-D of CWT scalogram in Fig. 10(c).

Fig. 9Experimental 2-D CWT and 3-D scalogram of unbalanced RK-4 with transverse crack at 1207 rpm: a) Y-Lateral deflection, b) 2-D CWT of unbalanced rotor with a crack, c) 3-D CWT scalogram of rotor with a crack

a)

b)

c)

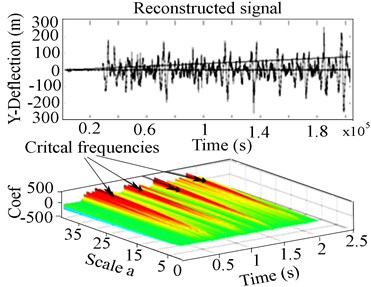
Fig. 10Experimental 2-D CWT and 3-D scalogram of the unbalanced RK-4 with a crack at 2216 rpm: a) Y-Lateral deflection, b) 2-D CWT of rotor with crack, c) 3-D CWT scalogram

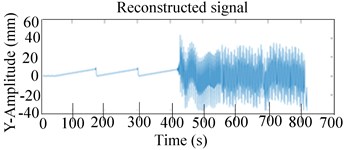
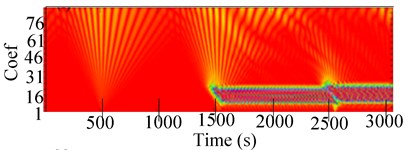
The latter observation was attributed to the effects of the crack as illustrated in Fig. 10(c). Two marginal spectral distributions by 3-D of CWT in Fig. 10(c) also show accumulated effect of energy of various frequencies different to that observed in Fig. 9(c). The CWT was sufficiently sensitive to local changes in the signal and revealed little changes in the response compared to the FFT. This analysis confirmed the effectiveness of CWT as a diagnostic tool for rotor cracks at a high rotation speed.

3.4. Dynamic vibration response of rotor excited by unbalance rotor-stator rub and a crack

In this section, rotors operate under tight rotor-stator clearances with a weak stiffness, which can become progressively worse if they are not well detected. For the coexisting faults case (i.e., unbalance, rotor-stator rub and crack), the time-domain response in lateral deflection, orbits and its FFT spectral are shown in this section. Consequently, the system was accelerated to a higher speed of 2216 rpm and the response near the rotor critical speed analysed using CWT. Evolutions of multiple faults phenomena at various motor speeds are presented in the Figs. 11 and 12.

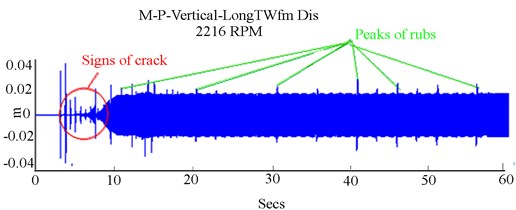
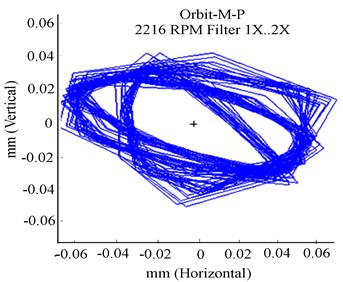
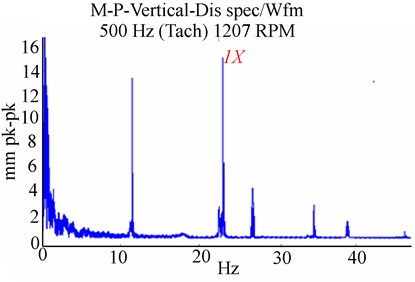
Fig. 11Experimental unbalanced RK-4 at higher speed 2216 rpm with rub and a crack Δ= 1.65×10-6m, ΔKξ/KYY= 0.55: a) Y-deflection, b) orbit response, c) Y-frequency

a)

b)

c)

When crack and rub co-exist, fault detection and monitoring become more complex. In Figs. 11(a) and 11(b), the crack and rub combined generated high vibration as indicated by vertical deflection and orbit patterns. Abnormal movements of the shaft in the bearing can be detected using orbit plots in Fig. 11(b); the X-Y of the orbit exhibit the severity of rub by producing highly random orbit plots. Due to high nonlinearity, the evolution of the orbit patterns and the associated noise peaks became considerably irregular for combined fault and the feature extraction accuracy is not evident.

Similar to the results obtained in [9], the presence of rub increases the rotor critical speed, but subsequently, the crack effect decreased shaft flexibility and decreased the critical speed of the multi-faulted rotor as observed in Fig. 11(a). The harmonic resonances 1X, 2X, 3X and 1/2X were observed in the FFT in Fig. 11(c), where the 1X was excited by unbalance, whereas the 2X, 3X (super-harmonic) occurred due to the crack and the 1/2X were excited by rub. With a maximum limit on frequency at 500 Hz, the RK-4 speed became extremely unstable in the range 1207-2216 rpm. It was not feasible to acquire measurements experimentally within this range. In Fig. 11, the response was characterised by a main peak at the synchronous frequency of 22.5 Hz. In Fig. 11(c) it was noted that for a given crack depth, unbalance excited the 1X sup-harmonic resonance, whereas rub excited the 1/2X and 1/3X sub-harmonic resonance.

Finally, it can be inferred that the emergence of the sub-harmonics, 2X and 3X provides evidence on the existence of a breathing crack and can be easily distinguished near the first critical speed. This inference concurs with the results in [9]. In Fig. 11(c), the amplitudes of the sub-harmonic and sup-harmonic resonance increased due to the interaction of rub, a breathing crack and unbalance at a high speed. The crack and noise induced the sub-harmonics, 2X and 3X in Fig. 11(c), which were of smaller magnitude compared to the 1X harmonic.

The trend in Fig. 11(c) suggests that the harmonics were sensitive to the rotor rotation speed. The results in Fig. 11 indicate that the effect of the crack on the rotor response was considerably larger than that of rub as the amplitude of the latter was largely attenuated in comparison to that of the former. Once again, the experimental results correlated well with the simulated results in [9].

As previously observed in Fig. 7 and Fig. 10, in the presence of rubs and breathing crack, the signal is highly disturbed; these fluctuations affect the accuracy of fault diagnosis. It is difficult to use these features with irregular fluctuations for an effective and accurate mixed faults diagnosis. To overcome this issue, a features extraction method using the vibration signals collected by the dynamic rotor data and processing by CWT is presented in Fig. 12.

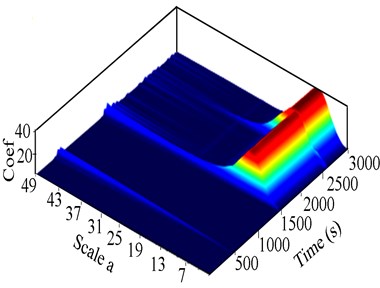
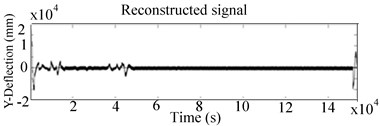
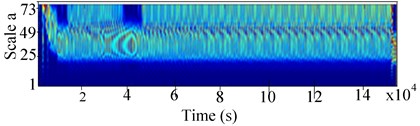
Fig. 12 shows the various versions of the system’s response under excitations by eccentric mass, crack and rub. The 2-D scalogram response in Fig. 12(a) exhibits few tight and small peaks harmonic frequencies at the beginning of the recorded signal, followed by multiple $nX$ high frequency bands and intermittent high energy emission in the CWT, which can be attributed to the recurrent rub-impact and noise effect. This observation corresponds to the rapid change in the system momentum at rub contact and the excitation by the crack. The vibration intensified at the first resonance point, after which the regular impact became more complex, depicting large irregular spots band represented by the coloured stretched noise in 2-D of Fig. 12 (b) at $t=$ 4028 s.

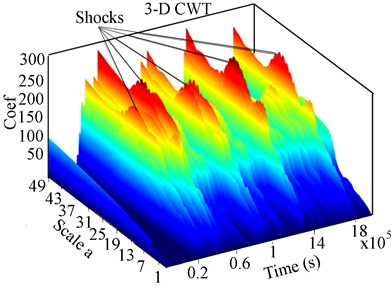
Fig. 12Experimental 2-D CWT and 3-D scalogram of the unbalance RK-4 rotor with crack and rub at 221 rpm: a) Y-Lateral deflection, b) 2-D CWT response, c) 3-D CWT scalogram

a)

b)

c)

Analysis in 3-D of Fig. 12(c) revealed a disproportionate concentration of energy at resonance, in the 3-D scalogram response. Rotor-stator contact indicated a huge exchange of accumulated effect of energy at various amplitudes. This was indicative of high energy emission (high energy impacts), the yellow-red colour in Fig. 12(c). The 3-D scalogram comprised a large spectrum of ridges, indicative of the recurrent rotor-stator contact. Various frequencies of shocks were detected at regular time ranges, but with distorted amplitudes for various reasons. Singular defects such as contact clearance, unsteady state and the anisotropic nature of the rotor were amongst these reasons. The difference between successive peaks was used to deduce the periodicity of shocks. The presence of peaks related to the second sub-critical speed due the effects of a crack was more evident in the CWT scalogram in Fig. 12(b) than in the time response.

In Fig. 12(b), the peaks were disproportional, indicating that high energy of rotor excitation occurred in the high frequency band. Referring to the 3-D CWT in Fig. 12(c), the effect of crack is indicated by the presence of disproportional ridges within the range of 0 to 3000 s, followed by the features of the rub-impact represented by the high accumulated effect energy at high coefficient (multiple small red crests observed). The scalogram analysis indicated that the centre of the concentrated energy corresponds to the most irregular regions. Analysis of the peaks features (yellow-red) appearance indicated the severity of the vibration. From the nature of the unbalance, rub-impact and crack collected response, the system was in a quasi-periodic motion.

The possible causes of the increase in vibration near the first and the second resonance were the fluctuation of the shaft’s stiffness during rotation and the energy emitted at rub-impact. Based on the above analysis, rub could be distinguished by the aperiodic changes of peaks in the CWT scalogram, whereas, a high variation of energy and frequency in the vicinity of the critical speed in CWT scalogram indicated a breathing crack. A combination of the breathing crack and rub in the system manifested complex evolutions in the CWT of 2-D and 3-D scalogram response of the experimental test data in Fig. 12.

In conjunction with the obtained experimental results, the proposed time-frequency technique for feature extraction can diagnose effectively and accurately unique and mixed faults on a rotor system. Therefore, this study experimentally confirms the validity of the CWT technique for feature extraction in identifying the RK-4 faults near the rotor critical speed.