Analysis of double-layer vibration isolation characteristics of ship power equipment

Cheng, Zhongyi; Cui, Jun; Zhao, Yamin; Jin, Mingrui; Cui, Junning

doi:10.21595/vp.2022.22562

Vibroengineering Procedia

Browse Procedia

Published: 21 April 2022

Check for updates

Analysis of double-layer vibration isolation characteristics of ship power equipment

Zhongyi Cheng¹

Jun Cui²

Yamin Zhao³

Mingrui Jin⁴

Junning Cui⁵

^{1, 3, 4, 5}Center of Ultra-precision Optoelectronic Instrument Engineering, Harbin Institute of Technology, Harbin, 150080, China

^{1, 3, 4, 5}Key Lab of Ultra-precision Intelligent Instrumentation (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin, 150080, China

²China Nuclear Power Technology Research Institute, Shenzhen, 518031, China

Corresponding Author:

Junning Cui

Cite the article Download PDF

Downloads 387

Abstract

The vibration isolation device of ship power equipment is the key equipment to protect it from damage, and its performance determines whether the ship can sail safely. To address the problem that it is difficult to achieve the optimal vibration isolation performance of ship’s double-layer vibration isolation, this paper establishes a vibration transmission theory model of ship’s power equipment double-layer vibration isolation system, derives the vibration displacement transmission rate formula based on the model, and studies the influence law of the stiffness ratio of the lower and upper layers of vibration isolation devices, the mass ratio of the intermediate raft frame to the power equipment and the damping of the upper and lower layers of vibration isolation devices on the vibration transmission. The results show that reducing the stiffness ratio of upper and lower layer vibration isolators and increasing the mass ratio of intermediate raft frame and power equipment can reduce the two resonant frequencies and narrow the interval between the two resonant frequencies, and increasing the damping of upper and lower layer vibration isolators can reduce the vibration peak at the two resonant frequencies, but the vibration isolation effect in the high frequency band becomes worse. It provides a theoretical basis for the design optimization of the double-layer vibration isolation system for ship's power equipment.

1. Introduction

When the ship is sailing at sea, the wave fluctuations and other external disturbances transmitted to the mechanical power equipment vibration will have a negative impact on mechanical equipment, and in serious cases even lead to power system paralysis [1]. The main means to solve this problem is to use elastic equipment for vibration isolation, and the main vibration isolation methods include single-layer vibration isolation, double-layer vibration isolation and floating raft vibration isolation. Among them, when single-layer vibration isolation is used for vibration isolation of large equipment at low speed, the support stiffness needs to be designed to be small and contradict the stability requirements of the system [2], but it is easier to ensure the shaft system alignment requirements, so it is widely used in ships with strict shaft system alignment requirements [3]-[5], and floating raft vibration isolation installs multiple power equipment on an intermediate raft frame, which can theoretically achieve better vibration isolation than double-layer vibration isolation [6]-[8], but due to its more complex structure, floating raft vibration isolation effect will be worse than double vibration isolation effect due to poor design. Therefore, double-layer vibration isolation is widely used on the ship power equipment.

In recent years, scholars at home and abroad have conducted a lot of research on double-layer vibration isolators [9]. Zhao et al. investigated the effect of different parameters of the system on the power flow transfer rate of the system under the action of external forces in the upper layer equipment [10]. Liu Haiping et al. proposed a double-layer highly damped vibration isolator consisting of positive and negative stiffness elements, and analyzed the mechanical transfer characteristics under the action of external forces, and studied its dynamics [11]. Zhang Wei et al. conducted a comparative study of the performance of integral and distributed double-layer vibration isolation systems [12]. Li Bin et al. conducted a theoretical analysis of the double-layer vibration isolation system and an experimental study of its vibration isolation performance [13]. However, none of the above literature analyzed the vibration transfer rate from the displacement transfer perspective to the upper ship equipment from the ship deck. But the study of the action law of each parameter on the vibration transmission rate in the double-layer vibration isolation system is the key to the reasonable design of the double-layer vibration isolation system.

This paper establishes the vibration transfer theory model of double-layer vibration isolation system for ship power system, derives the vibration transfer rate formula from the perspective of displacement transfer based on the model, and analyzes the influence of each parameter on the vibration transfer law, which provides a theoretical basis for the optimization of vibration isolation performance of ship power equipment.

2. Modeling of double-layer vibration isolation for ship power equipment

A typical double-layer vibration isolation model of a power unit is shown in Fig. 1(a), and its equivalent theoretical model is shown in Fig. 1(b), ignoring the mass of the vibration isolator. In Fig. 1(b), $m_{1}$ is the mass of the upper layer equipment, $k_{1}$ , $c_{1}$ are the stiffness and damping of the upper layer vibration isolation device respectively, and $m_{2}$ is the mass of the intermediate raft frame, $k_{2}$ , $c_{2}$ are the stiffness and damping of the lower layer vibration isolation device respectively. The displacement, velocity, and acceleration of the upper layer equipment are $x_{1} (t)$ , ${\dot{x}}_{1} (t)$ , and ${\ddot{x}}_{1} (t)$ , respectively, and those of the intermediate raft frame are $x_{2} (t)$ , ${\dot{x}}_{2} (t)$ , and ${\ddot{x}}_{2} (t)$ , respectively, and those of the ship deck are $u (t)$ , $\dot{u} (t)$ , $\ddot{u} (t)$ , respectively.

Fig. 1Double-layer vibration isolation model for ship power equipment: 1 – the upper layer equipment; 2 – the upper layer vibration isolation device; 3 – the intermediate raft frame; 4 – the lower layer vibration isolation device

Double-layer vibration isolation model for ship power equipment: 1 – the upper layer equipment; 2 – the upper layer vibration isolation device; 3 – the intermediate raft frame; 4 – the lower layer vibration isolation device

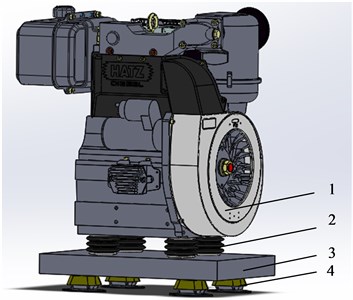
a) A typical double-layer vibration isolation model

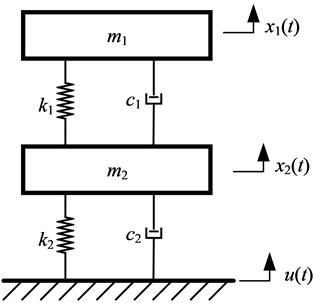
b) Equivalent theoretical model

The differential equation of motion of the system is:

1

\{\begin{array}{l} m_{2} {\ddot{x}}_{2} + k_{2} (x_{2} - u) + c_{2} ({\dot{x}}_{2} - \dot{u}) - k_{1} (x_{1} - x_{2}) - c_{1} ({\dot{x}}_{1} - {\dot{x}}_{2}) = 0, \\ m_{1} {\ddot{x}}_{1} + k_{1} (x_{1} - x_{2}) + c_{1} ({\dot{x}}_{1} - {\dot{x}}_{2}) = 0 . \end{array}

Take the Laplace transform of the Eq. (1) can obtain the system transfer function as follows:

2

H (s) = \frac{X_{1}}{U} = \frac{c_{2} s + k_{2}}{m_{1} s^{2} + (m_{2} s^{2} + c_{2} s + k_{2}) \cdot \frac{(m_{1} s^{2} + c_{1} s + k_{1})}{c_{1} s + k_{1}}},

where $ω_{10}$ , $ω_{20}$ are the resonant frequencies of the upper vibration isolation device and the lower vibration isolation device, $ξ_{1}$ , $ξ_{2}$ are the damping ratios of the upper vibration isolation device and the lower vibration isolation device, respectively, and satisfy the following relationship:

3

\{\begin{array}{l} ω_{10} = \sqrt{\frac{k_{1}}{m_{1}}}, ξ_{1} = \frac{c_{1}}{2 m_{1} ω_{10}}, \\ ω_{20} = \sqrt{\frac{k_{2}}{m_{2}}}, ξ_{2} = \frac{c_{2}}{2 m_{2} ω_{20}} . \end{array}

Substituting Eq. (3) into Eq. (2) to simplify and gives:

4

H (s) = \frac{4 m_{1} m_{2} ω_{10} ω_{20} ξ_{1} ξ_{2} \cdot s^{2} + 2 m_{1} ω_{10} ξ_{1} k_{2} \cdot s + 2 m_{2} ω_{20} ξ_{2} k_{1} \cdot s + k_{1} k_{2}}{G_{4} \cdot s^{4} + G_{3} \cdot s^{3} + G_{2} \cdot s^{2} + G_{1} s + k_{1} k_{2}},

where:

G_{4} = \frac{k_{1} k_{2}}{ω_{10}^{2} ω_{20}^{2}}, G_{3} = (\frac{k_{1}}{ω_{10}^{2}} \cdot 2 m_{2} ω_{20} ξ_{2} + \frac{k_{2}}{ω_{20}^{2}} \cdot 2 m_{1} ω_{10} ξ_{1} + \frac{k_{1}}{ω_{10}^{2}} \cdot 2 m_{1} ω_{10} ξ_{1}),

G_{2} = (\frac{k_{1} k_{2}}{ω_{10}^{2}} + \frac{k_{1} k_{2}}{ω_{20}^{2}} + 4 m_{1} m_{2} ω_{10} ω_{20} ξ_{1} ξ_{2} + \frac{k_{1}^{2}}{ω_{10}^{2}}), G_{1} = (2 m_{1} ω_{10} ξ_{1} k_{2} + 2 m_{2} ω_{20} ξ_{2} k_{1}) .

Transforming the Eq. (4) into the frequency domain transfer rate is as follows:

5

|H (ω)| = \sqrt{\frac{{(- 4 m_{1} m_{2} ω_{10} ω_{20} ξ_{1} ξ_{2} \cdot ω^{2} + k_{1} k_{2})}^{2} + {((2 m_{1} ω_{10} ξ_{1} k_{2} + 2 m_{2} ω_{20} ξ_{2} k_{1}) ω)}^{2}}{A^{2} + B^{2}}},

where:

A = (\frac{k_{1} k_{2}}{ω_{10}^{2} ω_{20}^{2}} ω^{4} - (\frac{k_{1} k_{2}}{ω_{10}^{2}} + \frac{k_{1} k_{2}}{ω_{20}^{2}} + 4 m_{1} m_{2} ω_{10} ω_{20} ξ_{1} ξ_{2} + \frac{k_{1}^{2}}{ω_{10}^{2}}) ω^{2} + k_{1} k_{2}),

B = (- ω^{3} (\frac{k_{1}}{ω_{10}^{2}} \cdot 2 m_{2} ω_{20} ξ_{2} + \frac{k_{2}}{ω_{20}^{2}} \cdot 2 m_{1} ω_{10} ξ_{1} + \frac{k_{1}}{ω_{10}^{2}} \cdot 2 m_{1} ω_{10} ξ_{1}) + ω (2 m_{1} ω_{10} ξ_{1} k_{2} + 2 m_{2} ω_{20} ξ_{2} k_{1})) .

3. Effect of different parameters on the effect of double-layer vibration isolation

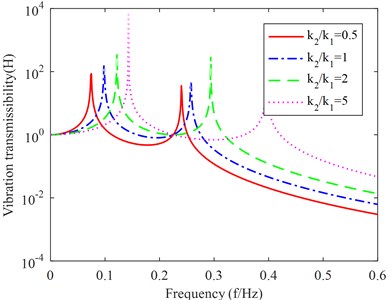
For the convenience of analysis, $m_{2} / m_{1}$ is the mass ratio and $k_{2} / k_{1}$ is the stiffness ratio. In order to analyse the relationship between the vibration transmission rate and the change of stiffness ratio, make the upper and lower vibration isolator damping ratio $ξ_{1} = ξ_{2} = 0$ , that is, ignore the influence of damping on the vibration transmission rate, make $m_{1} = m_{2} = 1$ , $k_{1} = 1$ , stiffness ratio of $k_{2} / k_{1} = 0.5$ , $k_{2} / k_{1} = 1$ , $k_{2} / k_{1} = 2$ , $k_{2} / k_{1} = 5$ to carry out analysis and calculation, and get the vibration transmission rate with the change of stiffness ratio as shown in Fig. 2.

Fig. 2Variation of vibration transmission rate with stiffness ratio

To study the variation of vibration transmission rate with mass ratio, make the upper and lower vibration isolator damping ratio $ξ_{1} = ξ_{2} = 0$ , that is, ignore the influence of damping on the vibration transmission rate, make $k_{1} = k_{2} = 1,$ $m_{1} = 1,$ mass ratio of $m_{2} / m_{1} = 0.5,$ $m_{2} / m_{1} = 1$ , $m_{2} / m_{1} = 2$ , $m_{2} / m_{1} = 5$ to carry out analysis and calculation, and get the vibration transmission rate with the change of stiffness ratio as shown in Fig. 3.

Fig. 3Variation of vibration transmission rate with mass ratio

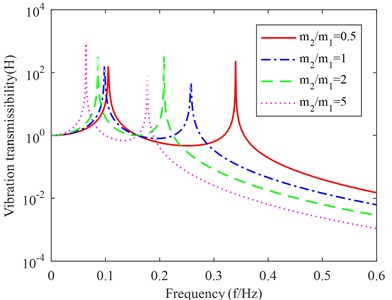
Fig. 4Variation of vibration transmission rate with damping ratio of upper vibration isolators

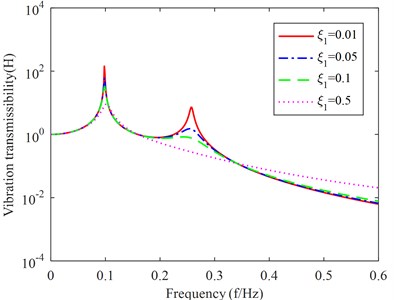
To analyze the variation of vibration transmission rate with the damping ratio of the upper layer, make $m_{1} = m_{2} = 1$ , $k_{1} = k_{2} = 1$ , $ξ_{2} = 0$ , and solve the vibration transmission curve when $ξ_{1} = 0.01$ , $ξ_{1} = 0.05$ , $ξ_{1} = 0.1$ , $ξ_{1} = 0.5$ respectively, and get the relationship between vibration transmission rate and upper layer damping ratio as shown in Fig. 4.

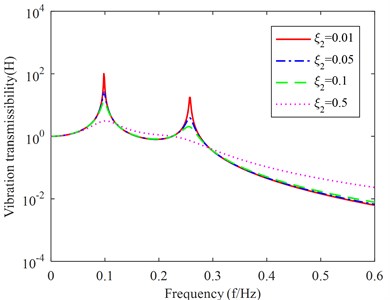
To analyze the variation of vibration transmission rate with the damping ratio of the lower layer, take $m_{1} = m_{2} = 1$ , $k_{1} = k_{2} = 1$ , $ξ_{1} = 0$ , and solve the vibration transmission curve when $ξ_{2} = 0.01$ , $ξ_{2} = 0.05$ , $ξ_{2} = 0.1$ , $ξ_{2} = 0.5$ respectively, and get the relationship between vibration transmission rate and upper layer damping ratio as shown in Fig. 5.

Fig. 5Variation of vibration transmission rate with damping ratio of lower vibration isolators

4. Conclusions

The above analysis shows that for the double-layer vibration isolation device of ship power equipment, there are two resonance peaks, and the vibration is attenuated in the frequency band after the first resonance peak, but the vibration is amplified at the second resonance frequency, and the vibration is attenuated in the frequency band after the second resonance frequency. The different mass ratio, stiffness ratio and damping of the upper and lower vibration isolation devices will have an effect on their vibration transmission characteristics, and the effect of different parameters on the vibration isolation effect of the system is as follows.

1) The smaller the stiffness ratio between the lower layer stiffness and the upper layer stiffness, the smaller the two resonant frequencies, while the smaller the interval between the two resonant frequencies, the better the vibration isolation effect, that is, the smaller the vibration transmitted to the power equipment by external vibration disturbances. However, in the case of smaller lower layer stiffness, the bearing capacity of the system will become worse.

2) The larger the mass ratio between the intermediate raft and the power equipment, the smaller the two resonant frequencies, and the smaller the interval between the two resonant frequencies, the better the vibration isolation effect, i.e., the smaller the vibration transmitted to the power equipment by external vibration disturbance. However, if the mass of the power equipment is known, increasing the mass ratio by increasing the mass of the intermediate raft will put forward higher requirements on the bearing capacity of the vibration isolator, and at the same time will greatly deplete the bearing capacity of the ship.

3) Increase the damping ratio of the upper layer vibration isolation device, can improve the first resonance peak and low frequency band vibration isolation effect, the second resonance peak because in the low frequency band will also be reduced, when the upper layer damping ratio increased to a certain extent will lead to the second resonance peak disappeared, but the high frequency band vibration isolation performance becomes worse.

4) Increase the damping ratio of the lower vibration isolation device can improve the vibration isolation effect near the two resonant frequencies, but the vibration isolation effect becomes worse in other frequency bands.

Therefore, when designing the double-layer vibration isolation device for ship power equipment, we should choose the appropriate middle raft mass and the stiffness of the upper and lower vibration isolators according to the actual situation of the isolated equipment, and try to increase the system damping to reduce the vibration transmission rate in the low frequency band and the two resonance peaks under the premise of meeting the vibration isolation performance in the high frequency band, so as to achieve the best vibration isolation effect.

References

X. L. Yao et al., “Numerical experiment methods for ship hull and equipment integrated analysis,” (in Chinese), Explosion and Shock Waves, Vol. 29, No. 4, pp. 367–374, 2009, https://doi.org/10.3321/j.issn:1001-1455.2009.04.006

Publisher
N. Niu et al., “Modeling and analysis of vibration characteristics of ship decentralized intermediate mass vibration isolation system,” (in Chinese), Ship Science and Technology, Vol. 42, No. 1, pp. 56–61, 2020, https://doi.org/10.3404/j.issn.1672-7649.2020.01.012

Publisher
Y. Y. Fang, G. H. Zhang, Y. F. Li, and P. Z. Qi, “Design of vibration isolation device for ship power equipment and investigation on its dynamic properties,” Applied Mechanics and Materials, Vol. 496-500, pp. 1129–1133, Jan. 2014, https://doi.org/10.4028/www.scientific.net/amm.496-500.1129

Publisher
L. Quanchao and Z. Rui, “Research of vibration characteristics of ship propeller-shaft longitudinal two-stage vibration isolation system,” in Journal of Physics: Conference Series, Vol. 1939, No. 1, p. 012103, May 2021, https://doi.org/10.1088/1742-6596/1939/1/012103

Publisher
Z. Cheng, J. Cui, Y. Zhao, and M. Jin, “Time domain response analysis of ship power equipment vibration isolation system under shock,” in 2021 IEEE 15th International Conference on Electronic Measurement and Instruments (ICEMI), pp. 141–145, Oct. 2021, https://doi.org/10.1109/icemi52946.2021.9679561

Publisher
J. Niu, K. Song, and C. W. Lim, “On active vibration isolation of floating raft system,” Journal of Sound and Vibration, Vol. 285, No. 1-2, pp. 391–406, Jul. 2005, https://doi.org/10.1016/j.jsv.2004.08.013

Publisher
Y. P. Xiong, J. T. Xing, and W. G. Price, “Power flow analysis of complex coupled systems by progressive approaches,” Journal of Sound and Vibration, Vol. 239, No. 2, pp. 275–295, Jan. 2001, https://doi.org/10.1006/jsvi.2000.3159

Publisher
M. S. Yu, G. R. Huang, and T. X. Fu, “Development review on mechanical-noise control for submarine,” (in Chinese), Journal of Ship Mechanics, Vol. 7, No. 4, pp. 110–120, 2003, https://doi.org/10.3969/j.issn.1007-7294.2003.04.015

Publisher
Y. Tao and H. T. Zhou, “Research on numerical simulation calculation of shock response in double-layer vibration isolation system,” (in Chinese), Noise and Vibration Control, Vol. 25, No. 3, pp. 1–4, 2005.

Search CrossRef
J. X. Zhao et al., “Vibration isolation performance analysis of double layer vibration isolation system,” (in Chinese), Chinese Journal of Ship Research, Vol. 12, No. 6, pp. 101–107, 2017, https://doi.org/10.3969/j.issn.1673-3185.2017.06.015

Publisher
H. P. Liu and J. Luo., “Study on the dynamic characteristics of a double-layered hyper-damping isolator,” (in Chinese), Transactions of Beijing Institute of Technology, Vol. 40, No. 1, pp. 17–22, 2020, https://doi.org/10.15918/j.tbit1001-0645.2018.395

Publisher
W. Zhang et al., “Comparative study on the vibration isolation performance between the entirety double-layer and distributed double-layer vibration isolation systems,” (in Chinese), Noise and Vibration Control, Vol. 37, No. 4, pp. 25–29, 2017, https://doi.org/10.3969/j.issn.1006-1355.2017.04.006

Publisher
B. Li, S. Guo, X. Mao, B. Cai, and B. Wang, “Characteristic analysis and experimental study of double layer vibration isolation device,” in IOP Conference Series: Materials Science and Engineering, Vol. 563, No. 3, p. 032037, Jul. 2019, https://doi.org/10.1088/1757-899x/563/3/032037

Publisher

About this article

Received

01 April 2022

Accepted

19 April 2022

Published

21 April 2022

SUBJECTS

Vibration control, generation and harvesting

DOI

https://doi.org/10.21595/vp.2022.22562

Keywords

ship vibration isolation

double-layer vibration isolators

vibration isolation characteristics

Acknowledgements

This research work is supported by the National Natural Science Foundation of China of No. 52075133.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 07 07

Experiment and analysis of active vibration isolation system based on rigid pedestal using SDOF actuator

Feng Xiong, Yan Li, Chunyu Wang

Research article

2020 03 31

Study on two-stage mounting systems having distributed intermediate mass

Zhengmin Li, Wei Xu

Research article

2020 03 31

Stability analysis of floating raft system under multiexcitation condition

Xin Li, Jinqiu Zhang

Research article

2018 09 24

Design and characteristic analysis of a novel quasi-zero-stiffness isolator using magnets as negative stiffness

Pan Su, Jiechang Wu, Shuyong Liu, Guanghui Chang, Junjie Shi, Lihua Yang

Z. Cheng, J. Cui, Y. Zhao, M. Jin, and J. Cui, “Analysis of double-layer vibration isolation characteristics of ship power equipment,” Vibroengineering PROCEDIA, Vol. 41, pp. 22–27, Apr. 2022, https://doi.org/10.21595/vp.2022.22562

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22562
UR  - https://doi.org/10.21595/vp.2022.22562
TI  - Analysis of double-layer vibration isolation characteristics of ship power equipment
T2  - Vibroengineering PROCEDIA
AU  - Cheng, Zhongyi
AU  - Cui, Jun
AU  - Zhao, Yamin
AU  - Jin, Mingrui
AU  - Cui, Junning
PY  - 2022
DA  - 2022/04/21
PB  - JVE International Ltd.
SP  - 22-27
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Cheng_2022,
	doi = {10.21595/vp.2022.22562},
	url = {https://doi.org/10.21595/vp.2022.22562},
	year = 2022,
	month = {apr},
	publisher = {{JVE} International Ltd.},
	pages = {22--27},
	author = {Zhongyi Cheng and Jun Cui and Yamin Zhao and Mingrui Jin and Junning Cui},
	title = {Analysis of double-layer vibration isolation characteristics of ship power equipment},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]Z. Cheng, J. Cui, Y. Zhao, M. Jin, and J. Cui, “Analysis of double-layer vibration isolation characteristics of ship power equipment,” Vibroengineering PROCEDIA, pp. 22–27, Apr. 2022, doi: 10.21595/vp.2022.22562.

Copy IEEE

Copied to clipboard!

Cheng, Zhongyi, Jun Cui, Yamin Zhao, Mingrui Jin, and Junning Cui. “Analysis of Double-Layer Vibration Isolation Characteristics of Ship Power Equipment.” Vibroengineering PROCEDIA, April 21, 2022, 22–27. https://doi.org/10.21595/vp.2022.22562.

Copy Chicago

Copied to clipboard!

Analysis of double-layer vibration isolation characteristics of ship power equipment

Abstract

1. Introduction

2. Modeling of double-layer vibration isolation for ship power equipment

3. Effect of different parameters on the effect of double-layer vibration isolation

4. Conclusions

References

About this article

Related Articles