Diffusion concentration distribution and numerical simulation of sulfate ions in polypropylene fiber concrete

Song, Mei; Zhang, Chongshang; Mi, Haichen; Wang, Ke; Wang, Shuai

doi:10.21595/vp.2022.22587

Vibroengineering Procedia

Browse Procedia

Published: 16 May 2022

Check for updates

Diffusion concentration distribution and numerical simulation of sulfate ions in polypropylene fiber concrete

Mei Song¹

Chongshang Zhang²

Haichen Mi³

Ke Wang⁴

Shuai Wang⁵

¹Weinan Highway Administration Bureau, Weinan, 714000, China

²Shaanxi Expressway Construction Group Corporation, Xi’an, 710064, China

³Xi’an Highway Research Institute, Xi’an, 710064, China

^{4, 5}School of Materials Science and Engineering, Chang’an University, Xi’an, 710064, China

Corresponding Author:

Chongshang Zhang

Cite the article Download PDF

Downloads 374

CrossRef Citations 1

Abstract

In order to analysis the sulfate diffusion process in polypropylene fiber concrete, the influence of the introduction of polypropylene fiber on the porosity was calculated at first based on the spatial distribution features of polypropylene fiber in concrete, which was classified into three types, penetration type, half through type and embedded type. On the basis of Fick’s second law and reaction kinetics equation, the diffusion model of sulfate ions in polypropylene concrete was established. The numerical solution was achieved with the adoption of finite difference method and the concentration of sulfate ions at any position can be calculated. At last, the numerical solution was verified using the results of polypropylene fiber reinforced concrete sulfate attack test. The results show that the relative error between numerical calculation and the actual test results is less than 17.65 %, the accuracy of the model is relatively high.

1. Introduction

Most of the existing researches are the experimental research on the mechanical properties of polypropylene fiber concrete based on the difference of its own materials (such as fiber content, fiber type, water-cement ratio, etc.), or the analysis of the sulfate diffusion process in plain concrete. There is little research on the diffusion law of sulfate in polypropylene fiber concrete and its meso numerical simulation [1-4]. Therefore, this paper studies the diffusion process of sulfate in polypropylene fiber concrete, establishes the diffusion model of sulfate in polypropylene fiber concrete, and uses sulfate erosion test to verify the numerical simulation results.

2. Diffusion model of sulfate ions in polypropylene fiber concrete

2.1. Change of concrete porosity

Assuming that fibers are randomly distributed in concrete, they can be divided into three types according to their spatial positions, as shown in Fig. 1.

2.1.1. Through type polypropylene fiber

The through type polypropylene fiber penetrates the whole concrete model element up and down. Its length is equal to the thickness of the model element, and it introduced open pores, the interface is in direct contact with the external erosive liquid through the openings at both ends. The expression of porosity ( $φ_{P F g}$ ) of through type polypropylene fiber is:

1

φ_{P F g} = 1 - \frac{V_{P F g}}{V} = 1 - \frac{N π d_{P F}^{2} H}{4 X L H} = 1 - \frac{π d_{P F}^{2} N}{4 X L},

where, $V_{P F g}$ represents the volume of through polypropylene fiber; $V$ represents the volume of polypropylene fiber concrete model element; $N$ represents the number of through polypropylene fibers in the polypropylene fiber concrete model element, which can be converted according to the volume content of polypropylene fibers; $d_{P F}$ represents the diameter of polypropylene fiber; $H$ represents the thickness of the model element, which is also the length of the through polypropylene fiber; $X$ represents the length of the model primitive; $L$ represents the width of the model primitive.

Fig. 1Distribution diagram of fiber in concrete

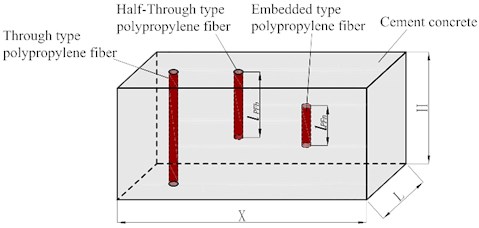
2.1.2. Half-Through type polypropylene fiber

The upper or lower end of the half-through type polypropylene fiber reaches the surface of the concrete model. The length of the polypropylene fiber is randomly distributed in the range of [0, $H$ ]. The pores introduced by it are open pores, and the interface is directly in contact with the external erosive liquid through the openings at the upper or lower end. The expression of porosity ( $φ_{P F b}$ ) of half-through type polypropylene fiber is:

2

φ_{P F b} = 1 - \frac{V_{P F b}}{V} = 1 - \frac{\sum_{i}^{n} π d_{P F}^{2} l_{P F b i}}{4 X L H} .

where, $V_{P F b}$ represents the volume of half-through type polypropylene fiber; $V$ represents the volume of polypropylene fiber concrete model element; $d_{P F}$ represents the diameter of polypropylene fiber; $l_{P F b i}$ represents the length of the ith half-through type polypropylene fiber, $l_{P F b i} \in [0, H]$ , $i = 0,1, 2 \dots n$ ; $X$ represents the length of the model primitive; $L$ represents the width of the model primitive; $H$ represents the thickness of the model primitive.

2.1.3. Embedded type polypropylene fiber

The embedded type polypropylene fiber is completely suspended in the concrete model element. The length of polypropylene fiber is randomly distributed in the range of (0, $H$ ), and the introduced pores are closed pores. The expression of porosity ( $φ_{P F n}$ ) of Embedded type polypropylene fiber is:

3

φ_{P F n} = \frac{c_{C A}}{c_{C A 0}} (1 - \frac{V_{P F n}}{V}) = \frac{c_{C A}}{c_{C A 0}} (1 - \frac{\sum_{i}^{n} π d_{P F}^{2} l_{P F n i}}{4 X L H}),

where, $c_{C A}$ represents the concentration of hydrated calcium aluminate in concrete; $c_{C A 0}$ represents the initial concentration of calcium aluminate in concrete; $V_{P F n}$ represents the volume of embedded polypropylene fiber; $V$ represents the volume of polypropylene fiber concrete model element; $d_{P F}$ represents the diameter of polypropylene fiber; $l_{P F n i}$ represents the length of the $i$ -th embedded polypropylene fiber, $l_{P F n i} \in (0, H)$ , $i = 0,1, 2 \dots n$ ; $X$ represents the length of the model primitive; $L$ represents the width of the model primitive; $H$ represents the thickness of the model primitive.

In the initial stage, because there are closed pores around the embedded polypropylene fiber, the interface will not contact with the external corrosive liquid. Sulfate reacts with cement hydration products to produce erosion products, which will gradually fill the pores in the concrete. As sulfate corrosion products continue to fill the pores in the concrete, microcracks will eventually occur. When the microcracks are located around the embedded polypropylene fiber, connecting pores will be formed. At this time, the cement mortar around the embedded polypropylene fiber will contact the erosion solution through the connecting pores.

2.1.4. Initial porosity of polypropylene fiber reinforced concrete

Regardless of the filling effect of erosion products on the pores, the initial porosity in the concrete can be expressed as:

4

φ_{0} = M a x (f_{V c} \frac{w_{c} - 0.39 h_{α}}{w_{c} + 0.32}, 0) + φ_{0 P F},

where, $f_{V c}$ represents the volume fraction of cement; $h_{α}$ represents the hydration degree of cement; $w_{c}$ represents the water cement ratio; $φ_{0 P F}$ represents the initial porosity introduced by polypropylene fiber.

The degree of hydration $h$ can be expressed as $h_{α} = 1 - 0.5 [{(1 + 1.67 t)}^{- 0.6} + {(1 + 0.29 t)}^{- 0.48}]$ , where $t$ represents the time of cement hydration.

The initial porosity introduced by polypropylene fiber can be expressed as:

5

φ_{0 P F} = φ_{P F g} + φ_{P F b},

where, $φ_{P F g}$ represents the porosity of the penetrating polypropylene fiber; $φ_{P F b}$ represents the porosity of the semi-penetrating polypropylene fiber.

2.1.5. Polypropylene fiber concrete filled porosity

The filling of ettringite will affect the porosity of concrete. The porosity of concrete filled with ettringite can be expressed as:

6

φ_{p r o d} = M i n [\frac{1}{q} \sum_{i = 1}^{3} (\frac{V_{c A i}}{m_{v - C H}} - \frac{γ_{i}}{m_{v - C H}}) C_{C A}, f φ_{0}] + φ_{P F n},

where, Min is the minimum function; $V_{c A 1}$ , $V_{c A 2}$ , $V_{c A 3}$ respectively represent the volume consumption of $C_{4} A H_{13}$ , $C_{4} A \bar{S} H_{12}$ and $C_{3} A$ in the chemical reaction process in the concrete; $m_{v - C H}$ represents the molar volume of calcium hydroxide; $γ_{i}$ represents the reaction coefficient of ettringite by reaction of tricalcium aluminate with gypsum; $f$ represents the volume fraction of the initial porosity after the ettringite is filled with capillary pores; $φ_{P F n}$ represents the porosity of the embedded polypropylene fiber.

Under sulfate attack, the porosity of the concrete is reduced due to the filling of erosion products. Then: $φ = M a x [(φ_{0} - φ_{p r o d}), 0]$ .

2.2. Concentration distribution of sulfate ions

It is assumed that polypropylene fiber concrete meets the following conditions: saturation; isotropy; porous material, the diffusion coefficient of sulfate ions in concrete is a function of time. When polypropylene fiber concrete is exposed to a sulfate environment for a long time, ${S O}_{4}^{2 -}$ will gradually diffuse from both sides to the inside. The erosion model of concrete is assumed to be one-dimensional symmetric model, then the erosion model is shown in Fig. 2.

Fig. 2Sulfate erosion model

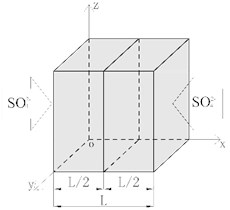
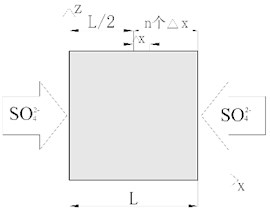
Fig. 3Sulfate erosion plane sketch

2.2.1. Diffusion reaction equation

The diffusion reaction equation of ${S O}_{4}^{2 -}$ can be deduced by using Fick’s second law and chemical reaction kinetic equation as [5]:

7

\{\begin{array}{l} \frac{\partial C}{\partial t} = \frac{\partial}{\partial x} \{D_{C} (x, t) \frac{\partial C}{\partial x}\} + \frac{\partial C_{d}}{\partial t}, \\ C (x, 0) = 0, x \in Π, \\ C (0, t) = C_{0}, C (L, t) = C_{0}, \end{array}

where, $C$ represents the concentration of ${S O}_{4}^{2 -}$ ; $x$ represents the position coordinates; $t$ represents the diffusion time of ${S O}_{4}^{2 -}$ in concrete; $D_{C}$ represents the diffusion coefficient of sulfate ions; $C_{d}$ represents the concentration consumed by ${S O}_{4}^{2 -}$ due to chemical reactions; $C_{0}$ represents ${S O}_{4}^{2 -}$ The boundary concentration; $Π$ represents the cross-sectional area; $L$ represents the thickness of the concrete specimen.

2.2.2. Diffusion coefficient

There is electrolyte solution containing Na⁺, K⁺, OH^-, Ca²⁺, ${S O}_{4}^{2 -}$ and other ions in the internal pores of the concrete. According to Davis model [6] and the Mode Coupling Theory Method of Electrolyte Friction Electrolyte [7] and other electrolyte solution theory, the diffusion coefficient of ${S O}_{4}^{2 -}$ in concrete can be expressed as [8]:

8

D_{c} = \frac{φ R T}{τ_{c} z^{2} F^{2}} \{1 - [\frac{1}{{4 \sqrt{I} (1 + α B \sqrt{I})}^{2}} \frac{0.1 - 4.17 \times 10^{- 5} I}{\sqrt{1000}}] A c z^{4}\}

∙ [Λ^{0} - (C Z^{2} + D z^{3} ω Λ^{0}) \sqrt{c}],

where, $φ$ represents the saturated porosity after the erosion product fills the capillary pores, which is given by Eq. (10); $R$ represents the gas constant; $T$ represents the ambient temperature; $τ_{c}$ represents the tortuosity of the transmission path in the concrete before the erosion product fills the capillary pores, It is given by Eq. (11); $z$ represents the valence of ${S O}_{4}^{2 -}$ ; $F$ represents Faraday’s constant; $I$ represents ionic strength, which is given by Eq. (10); $α$ represents ${S O}_{4}^{2 -}$ radius; $Λ^{0}$ represents ${S O}_{4}^{2 -}$ conductivity; $ω$ represents ionic Activity coefficient; $c$ represents the concentration of sulfur ${S O}_{4}^{2 -}$ ; $A$ , $B$ , $C$ and $D$ are parameters related to temperature, which can be expressed by Eq. (9):

9

A = \frac{\sqrt{2} e F^{2}}{{8 π (ε_{0} ε_{r} R T)}^{\frac{3}{2}}}, B = \sqrt{\frac{2 F^{2}}{ε_{0} ε_{r} R T}}, C = \frac{\sqrt{2} e F^{2}}{3 π η \sqrt{1000 ε_{0} ε_{r}} R T}, D = \frac{\sqrt{2} e F^{2}}{{3 \sqrt{1000} (ε_{0} ε_{r} R T)}^{\frac{3}{2}}},

where, $e$ represents the elementary charge; $ε_{0}$ represents the vacuum dielectric constant; $ε_{r}$ represents the relative dielectric constant; $η$ represents the viscosity of water.

The ion concentration in polypropylene fiber concrete can be calculated according to the theory of electrolyte solution:

10

I = \frac{1}{2} \sum_{i = 1}^{N} {z_{i}}^{2} c_{i},

where, $N$ represents the number of types of ions; $z_{i}$ represents the valence of the $i$ -th ion in the solution; $c_{i}$ represents the initial concentration of the ion in the solution.

2.2.3. Tortuosity of erosion path

According to the material composition, distribution state and geometric characteristics of polypropylene fiber concrete, the geometric model of the tortuosity of the erosion path can be express:

11

τ_{c} = η_{s a} η_{s t} (1 + 0.35 \sqrt{f_{s a}}) (1 + 0.35 \sqrt{f_{s t}}) τ_{c p},

where, $η_{s t}$ and $f_{s t}$ represent the shape factor and volume rate of the sand, respectively; $η_{s a}$ and $f_{s a}$ represent the shape factor and volume rate of the crushed stone, respectively; $τ_{c p}$ represents the tortuosity of the sulfate transmission path in the cement paste, which can be expressed by Eq. (12) express:

12

τ_{c p} = ω_{w c} η_{r} h_{a} [\frac{1}{1 - \sqrt{1 - φ}} \sqrt{{(1 - \sqrt{1 - φ})}^{2} + 1 / 4}],

where, $ω_{w c}$ represents the adjustment coefficient; $η_{r}$ represents the shape factor of the cement particles.

2.2.4. Concentration distribution

Assuming that the external sulfate ion concentration on both sides of polypropylene fiber concrete is $C_{0}$ , the diffusion reaction equation of ${S O}_{4}^{2 -}$ can be solved according to a one-dimensional symmetry problem. By analyzing the distribution of ${S O}_{4}^{2 -}$ in the concrete range of $L$ /2, we can get the erosion of ${S O}_{4}^{2 -}$ on the whole concrete, as shown in Fig. 3. According to the above analysis, the diffusion reaction equation of ${S O}_{4}^{2 -}$ erosion polypropylene fiber concrete model can be established as follows:

13

\frac{\partial C}{\partial t} = \frac{\partial}{\partial x} \{D_{C} (x, t) \frac{\partial C}{\partial x}\} + \frac{\partial C_{d}}{\partial t} .

By iterative solution of catch-up method, the concentration distribution of ${S O}_{4}^{2 -}$ in concrete at any time can be obtained.

2.3. Method of specimen

In this experiment, P·O42.5 ordinary Portland cement and grade Ⅰ fly ash were used as cementing materials, and the replacement of fly ash was 20 %. Fine aggregate was made of continuously graded fine sand with particle size of 0-4.75 mm, fineness modulus of 2.68, apparent density of 2.64 g/cm³. Gravel is limestone gravel with continuous gradation of 5-20 mm in diameter. The water was ordinary drinking tap water with a water-cement ratio of 0.32. The fiber is polypropylene fiber (PF), and its physical and mechanical properties are shown in Table 1. Forming 100 mm×100 mm×400 mm concrete specimen.

Table 1Physical and mechanical properties of polypropylene fiber

Fiber type	Density (g/cm³)	Equivalent diameter (μm)	Tensile strength (MPa)	Elastic modulus (MPa)	Elongation at break (%)
Fascicular monofilament	0.91	21	≥ 400	≥ 3500	8-30

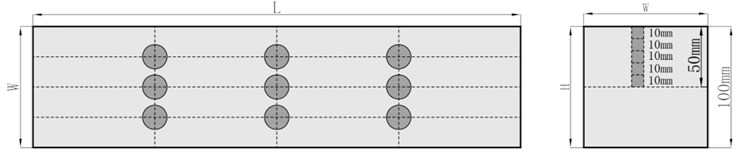
Erosion method: Put the polypropylene fiber concrete specimens (100 mm×l00 mm×400 mm) cured to the specified age into a 5 % Na₂SO₄ solution for long-term soaking. The long-term immersion test takes 30 d as a cycle, that is, take out the test block after soaking in Na₂SO₄ solution for 30 d, 60 d, 90 d, 120 d... And wipe the surface moisture of the test block with a rag. After natural air drying, drill core sampling, and the distribution of sampling drilling points is shown in Fig. 4.

Fig. 4Specimen sampling drilling point distribution diagram

2.4. Comparison between experimental results and numerical simulation results

Fig. 5 shows the changes of theoretical and experimental values of ${S O}_{4}^{2 -}$ concentration at different depths (0 mm, 10 mm, 20 mm, 30 mm, 40 mm and 50 mm) in concrete specimens soaked with 5 % sodium sulfate solution for 0 d, 30 d, 60 d, 90 d, 120 d and 150 d respectively.

Fig. 5Relative error statistics of simulation results and the test results (%)

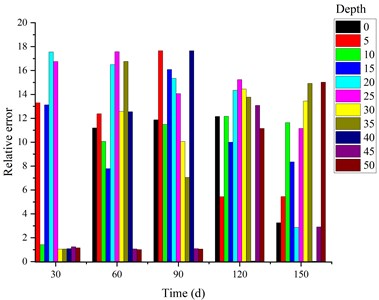
It can be seen from Fig. 5 that the maximum relative difference between the theoretical calculation results and the test results shall not exceed 17.65 %. However, in the period of 0 d-90 d, the theoretical calculation value increases more significantly than the measured value. The error between the two groups of data is concentrated between 12.38 %-17.65 %, and the error is relatively large, indicating that the diffusion speed of erosion ions is relatively fast in the theoretical model calculation; In the period of 90 d ~ 150 d, the theoretical calculated values tend to be consistent with the measured values. The relative error between the two groups of data is concentrated between 10.00 %-15.24 %, and the error gradually decreases, indicating that the erosion ions diffusion reaction reaches a relatively stable state during this period, and the actual test is less affected by the external test conditions.

3. Conclusions

1) Based on the spatial distribution characteristics of polypropylene fiber in concrete, the spatial distribution of polypropylene fiber is divided into through type, half-through type and embedded type. The porosity of three types of polypropylene fiber is calculated respectively, and the initial porosity and filling porosity of polypropylene fiber concrete are calculated respectively according to the process of sulfate eroding concrete structures.

2) Based on Fick’s second law and reaction kinetics theory, the diffusion model of ${S O}_{4}^{2 -}$ in polypropylene fiber concrete is established. The finite difference method is used to realize the numerical solution, the sulfate erosion migration law in polypropylene fiber concrete is studied, and the numerical solution of ${S O}_{4}^{2 -}$ concentration at any position $(X_{i}, T_{j})$ is realized.

3) In this paper, the sulfate erosion test of polypropylene fiber reinforced concrete is designed, and the sulfate ion concentration of the specimen at different time and depth under the erosion condition of 5 % sodium sulfate solution is quantitatively measured, which is compared with the theoretical calculation value of the established sulfate erosion model of polypropylene fiber reinforced concrete. The results show that the relative error between the model calculation results and the actual test results is less than 17.65 %, and the accuracy is high.

References

Q. Song, J. Nie, D. Wu, Y. Hu, and Y. Chen, “Effect of SO42−, Cl− and Mg2+ on the system of C-S-H and Ca(OH)2,” Construction and Building Materials, Vol. 285, p. 122955, May 2021, https://doi.org/10.1016/j.conbuildmat.2021.122955

Publisher
X. Qiao and J. Chen, “Correlation of propagation rate of corrosive crack in concrete under sulfate attack and growth rate of delayed ettringite,” Engineering Fracture Mechanics, Vol. 209, pp. 333–343, Mar. 2019, https://doi.org/10.1016/j.engfracmech.2019.01.036

Publisher
B. Ali, S. S. Raza, I. Hussain, and M. Iqbal, “Influence of different fibers on mechanical and durability performance of concrete with silica fume,” Structural Concrete, Vol. 22, No. 1, pp. 318–333, Feb. 2021, https://doi.org/10.1002/suco.201900422

Publisher
M. R. Latifi, Biricik, and A. Mardani Aghabaglou, “Effect of the addition of polypropylene fiber on concrete properties,” Journal of Adhesion Science and Technology, Vol. 36, No. 4, pp. 345–369, Feb. 2022, https://doi.org/10.1080/01694243.2021.1922221

Publisher
X. B. Zuo, “Modeling ion diffusion-reaction behavior in concrete associated with durability deterioration subjected to couplings of environmental and mechanical loadings,” Nanjing, School of Materials Science and Engineering, Southeast University, 2011.

Search CrossRef
E. Samson, J. Marchand, J. L. Robert, and J. P. Bournazel, “Modelling ion diffusion mechanisms in porous media,” International Journal of Numerical Methods in Engineering, Vol. 46, No. 12, pp. 2043–2060, 1999, https://doi.org/10.1002/(sici)1097-0207(19991230)46:12

Publisher
A. Chandra and B. Bagchi, “Ion conductance in electrolyte solutions,” The Journal of Chemical Physics, Vol. 110, No. 20, pp. 10024–10034, May 1999, https://doi.org/10.1063/1.478876

Publisher
W. Sun and C. Yu, “Modeling of ion diffusion coefficient in saturated concrete,” Computers and Concrete, Vol. 7, No. 5, pp. 421–435, Oct. 2010, https://doi.org/10.12989/cac.2010.7.5.421

Publisher

Cited by

Influence of Fiber Orientation on the Water and Ions Transportation of Engineered Cementitious Composite (ECC)

(2023)

About this article

Received

09 April 2022

Accepted

09 May 2022

Published

16 May 2022

SUBJECTS

Materials and measurements in engineering

DOI

https://doi.org/10.21595/vp.2022.22587

Keywords

polypropylene fiber concrete; sulfate attack; numerical simulation; porosity; ionic diffusion

Acknowledgements

The research was supported by the Transportation Science and Technology Project in Shaanxi Province (Nos. 20-16 K), the Key R&D Program in Shaanxi Province (No. 2019GY-422).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 10 22

Failure mechanism on sulfate attack and dissolved corrosion of diseased tunnel lining structure

Jinwang Mao, Ninghui Liang, Ru Yan

Research article

2021 06 28

Study on temperature control and crack resistance of mass concrete anchorage in suspension bridge

Shuyang Liu, Zewei Yin

Research article

2020 05 15

Effects of combustion parameters on antiexplosion performance: model tests and numerical simulations

Mingxin Bai, Xianglian Xu, Hongxing Yang, Meng Xiong, Wenqiang Zhu, Zhaopeng Liu, Chenhu Luo

Research article

2019 06 30

Numerical simulation of hydraulic fracturing in transversely isotropic rock masses based on PFC-2D

Lei Xia, Yawu Zeng

M. Song, C. Zhang, H. Mi, K. Wang, and S. Wang, “Diffusion concentration distribution and numerical simulation of sulfate ions in polypropylene fiber concrete,” Vibroengineering PROCEDIA, Vol. 42, pp. 95–101, May 2022, https://doi.org/10.21595/vp.2022.22587

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22587
UR  - https://doi.org/10.21595/vp.2022.22587
TI  - Diffusion concentration distribution and numerical simulation of sulfate ions in polypropylene fiber concrete
T2  - Vibroengineering PROCEDIA
AU  - Song, Mei
AU  - Zhang, Chongshang
AU  - Mi, Haichen
AU  - Wang, Ke
AU  - Wang, Shuai
PY  - 2022
DA  - 2022/05/16
PB  - JVE International Ltd.
SP  - 95-101
VL  - 42
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Song_2022,
	doi = {10.21595/vp.2022.22587},
	url = {https://doi.org/10.21595/vp.2022.22587},
	year = 2022,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {42},
	pages = {95--101},
	author = {Mei Song and Chongshang Zhang and Haichen Mi and Ke Wang and Shuai Wang},
	title = {Diffusion concentration distribution and numerical simulation of sulfate ions in polypropylene fiber concrete},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]M. Song, C. Zhang, H. Mi, K. Wang, and S. Wang, “Diffusion concentration distribution and numerical simulation of sulfate ions in polypropylene fiber concrete,” Vibroengineering PROCEDIA, vol. 42, pp. 95–101, May 2022, doi: 10.21595/vp.2022.22587.

Copy IEEE

Copied to clipboard!

Song, Mei, Chongshang Zhang, Haichen Mi, Ke Wang, and Shuai Wang. “Diffusion Concentration Distribution and Numerical Simulation of Sulfate Ions in Polypropylene Fiber Concrete.” Vibroengineering PROCEDIA 42 (May 16, 2022): 95–101. https://doi.org/10.21595/vp.2022.22587.

Copy Chicago

Copied to clipboard!

Diffusion concentration distribution and numerical simulation of sulfate ions in polypropylene fiber concrete

Abstract

1. Introduction

2. Diffusion model of sulfate ions in polypropylene fiber concrete

2.1. Change of concrete porosity

2.1.1. Through type polypropylene fiber

2.1.2. Half-Through type polypropylene fiber

2.1.3. Embedded type polypropylene fiber

2.1.4. Initial porosity of polypropylene fiber reinforced concrete

2.1.5. Polypropylene fiber concrete filled porosity

2.2. Concentration distribution of sulfate ions

2.2.1. Diffusion reaction equation

2.2.2. Diffusion coefficient

2.2.3. Tortuosity of erosion path

2.2.4. Concentration distribution

2.3. Method of specimen

2.4. Comparison between experimental results and numerical simulation results

3. Conclusions

References

Cited by

About this article

Related Articles