A new frequency estimation method for a real-valued waveform with multiple sub-Nyquist channels based on the ESPRIT algorithm

Wang, Lulu; Liu, Shang

doi:10.21595/vp.2022.22835

Vibroengineering Procedia

Browse Procedia

Published: 25 August 2022

Check for updates

A new frequency estimation method for a real-valued waveform with multiple sub-Nyquist channels based on the ESPRIT algorithm

Lulu Wang¹

Shang Liu²

¹College of Mechanical and Electronic Engineering, Northwest A&F University, Xianyang, China

²College of Automation Science and Electrical Engineering, Beihang University, Beijing, China

Corresponding Author:

Lulu Wang

Cite the article Download PDF

Downloads 305

Abstract

Real-valued waveform frequency measurement problems are often encountered in signal processing and they can be solved by designing a linear system. However, they require the sampling frequency to reach twice the maximum of the measured frequency, that is, to meet the Nyquist condition, which in many cases cannot be satisfied considering the hardware limitation. Therefore, how to design a nonlinear method to reconstruct the signal frequency is of great significance. To solve the frequency estimation problem for a real-valued waveform with sub-Nyquist channels, we propose a frequency estimator based on multiple sub-Nyquist channels. Our algorithm mainly consists of the following parts: 1) Calculate the folded frequencies which are lying on the first Nyquist region for each channel based on ESPRIT. 2) Reconstruct the signal frequency by a search method according to the set of folded frequencies. Finally, the simulation results verify the good performance of our proposed algorithm.

1. Introduction

In practice, measurements of high-frequency signals are often used in the field of radar signals [1] and infinite sensors [2]. Most current frequency estimation algorithms are based on the Nyquist theorem, which can estimate the signal in the time domain based on the differential linear relationship or map the signal from the time domain to the frequency domain based on the linear Fourier transform. However, as the signal bandwidth increases, those methods often require ADCs with a high sampling rate, which is very expensive and sometimes difficult to implement [3]. Therefore, how to reconstruct the signal frequency using the sub-Nyquist channel is an important nonlinear reconstruction problem.

The development of the Chinese remainder theorem (CRT) provides a possible solution to solve this nonlinear reconstruction problem. The traditional search-based CRT method is proposed in [4-5], but it is time-consuming and requires the sampling frequency to be coprime. The closed-form CRT proposed in [6-7] can further reduce the operation complexity while improving the generalizability of the algorithm. However, to use the CRT reconstruction method, we need to filter out the true residual from the two folded frequencies which are symmetrical about half of the sampling frequency. In practice, it is hard to select the correct residue. Therefore, the CRT is mostly applicable only in the frequency estimation for complex signals. To measure the frequency of the real-valued signal, Huang [8] added a zero-crossing detector in front of the sampling channel and selected the right remainder according to the signal phase. But this method has a limited noise immunity considering that the signal phase is easily affected by noise.

Maroosi [9] gave the theoretical upper bound of the real-valued signal frequency for stable reconstruction. Based on Maroosi’s work, Su [10] proposed an estimator with better noise immunity based on least squares and a search algorithm that does not depend on the phase of the signal. We further propose a new real-valued signal frequency estimation method based on [9-10], which improves the estimation accuracy and specifies the sampling requirements of this search algorithm. The simulation experiments demonstrate that our estimator does have better accuracy compared to [10].

Fig. 1System overall flow chart

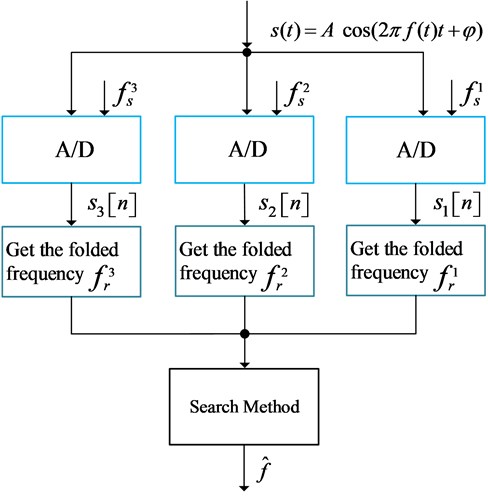
2. Frequency estimator using multiple sub-Nyquist channels

2.1. Estimator overview

Our proposed multi-channel-based frequency estimator for high-frequency signals is shown in Fig. 1. First, the signal is under sampled through multiple ADC channels. Then we obtain the residual frequency of the signal frequency in each channel according to the ESPRIT algorithm. Finally, we use the search-based method to reconstruct the signal frequency according to the set of sampling frequencies and residual frequencies obtained in the previous step.

2.2. Obtaining folded frequency

If we use an ADC with a sampling frequency of $f_{s}$ to undersample the signal with frequency $f$ , the digital signal sequence is as follows:

1

s [n] = A c o s (\frac{2 π f}{f_{s}} n + φ) + w [n],

where the $w [n]$ is the signal noise. Considering that the signal frequency may be greater than the sampling frequency, we have:

2

f = Q f_{s} + f_{r}, Q \in N_{+},

where we denote the $f_{r}$ as the folded frequency or the residue of the signal frequency moduli the sampling frequency. Thus, we can rewrite Eq. (1) as:

3

s [n] = A c o s (\frac{2 π f_{r}}{f_{s}} n + φ) + w [n] .

Considering that:

4

A c o s (\frac{2 π f_{r}}{f_{s}} n + φ) = \frac{1}{2} A (e^{i (\frac{2 π f_{r}}{f_{s}} n + φ)} + e^{- i (\frac{2 π f_{r}}{f_{s}} n + φ)}) .

Thus, the signal sequence model is as follows:

5

(\binom{\begin{matrix} \begin{matrix} s [0] \\ s [1] \end{matrix} \\ \dots \end{matrix}}{s [N - 1]}) = (\begin{matrix} \begin{matrix} 1 & 1 \\ e^{i (\frac{2 π f_{r}}{f_{s}})} & e^{- i (\frac{2 π f_{r}}{f_{s}})} \end{matrix} \\ \begin{matrix} \dots & \dots \\ e^{(N - 1) i (\frac{2 π f_{r}}{f_{s}})} & e^{- (N - 1) i (\frac{2 π f_{r}}{f_{s}})} \end{matrix} \end{matrix}) (\begin{matrix} \frac{A}{2} e^{i φ} \\ \frac{A}{2} e^{- i φ} \end{matrix}) + (\binom{\begin{matrix} \begin{matrix} w [0] \\ w [1] \end{matrix} \\ \dots \end{matrix}}{w [N - 1]}) .

We denote that:

6

s = (s [0], s [1], . . ., s [N - 1])^{T},

P_{1} = (\begin{matrix} \begin{matrix} 1 & 1 \\ e^{i (\frac{2 π f_{r}}{f_{s}})} & e^{- i (\frac{2 π f_{r}}{f_{s}})} \end{matrix} \\ \begin{matrix} \dots & \dots \\ e^{(N - 1) i (\frac{2 π f_{r}}{f_{s}})} & e^{- (N - 1) i (\frac{2 π f_{r}}{f_{s}})} \end{matrix} \end{matrix}), P_{2} = (\begin{matrix} \begin{matrix} e^{i (\frac{2 π f_{r}}{f_{s}})} & e^{- i (\frac{2 π f_{r}}{f_{s}})} s \\ e^{2 i (\frac{2 π f_{r}}{f_{s}})} & e^{- 2 i (\frac{2 π f_{r}}{f_{s}})} \end{matrix} \\ \begin{matrix} \dots & \dots \\ e^{N i (\frac{2 π f_{r}}{f_{s}})} & e^{- N i (\frac{2 π f_{r}}{f_{s}})} \end{matrix} \end{matrix}),

Φ = (\begin{matrix} e^{i (\frac{2 π f_{r}}{f_{s}})} \\ 0 \end{matrix} \begin{matrix} 0 \\ e^{- i (\frac{2 π f_{r}}{f_{s}})} \end{matrix}), w = (\binom{\begin{matrix} \begin{matrix} w [0] \\ w [1] \end{matrix} \\ \dots \end{matrix}}{w [N - 1]}) .

To obtain $f_{r}$ , we choose the widely used parameter estimation method ESPRIT [11] (Estimation of Signal Parameters Via Rotational Invariance Techniques) based on signal eigenspace.

Thus we have: $P_{2} = P_{1} Φ$ and we can also find selection matrix $J_{1}$ and $J_{2}$ which satisfy:

7

J_{2} P_{2} = J_{1} P_{1} Φ .

Based on the signal sequence $s$ , we can build the autocorrelation matrix:

8

R_{s s} = s s^{H} .

Thus, we can obtain the eigenvector matrix $V$ which could span the signal subspace through eigenvalue decomposition of $R_{s s}$ . Therefore, we could find a full rank matrix $T$ which satisfies:

9

P = V T .

Considering Eq. (7), we have:

10

T Φ T^{H} = J_{1}^{- 1} V^{- 1} J_{2} V .

We find an eigen decomposition of $T Φ T^{H}$ and finally we have:

11

f_{r} = \frac{f_{s}}{2 π} a r g (e i g e n v a l (T Φ T^{H})) .

2.3. Signal frequency reconstruction

As we have obtained the folded frequency $f_{r}$ and ${f_{s} - f}_{r}$ in Section 2.2, we can choose the one $f_{r t}$ from $f_{r}$ and ${f_{s} - f}_{r}$ which satisfies $0 < f_{r t} < \frac{f_{s}}{2}$ .

Thus, we have the following reconstruction model:

12

f = p^{i} f_{s}^{i} + q^{i} f_{r t}^{i}, p^{i} \in N_{+}, q^{i} \in \{- 1,1\},

where the $f_{s}^{i}$ denotes the sampling frequency in the $i$ th AD channel and $f_{r t}^{i}$ denotes the selected folded frequency in the $i$ th AD channel. Maroosi [9] gave the reconstruction upper bound as:

13

f_{m a x 1} = \frac{m i n \{\begin{matrix} f_{s}^{1} + l c m (f_{s}^{2}, f_{s}^{3}) \\ f_{s}^{2} + l c m (f_{s}^{1}, f_{s}^{3}) \\ f_{s}^{3} + l c m (f_{s}^{1}, f_{s}^{2}) \end{matrix}\}}{2} .

In other words, we can reconstruct the signal frequency without aliasing only if $f < f_{m a x 1}$ .

As we have three channels, there exist too many parameter combinations of $p^{i} \in N_{+}$ and $q^{i}$ for $i \in {1,2, 3}$ . To reduce the search complexity, we add a constraint to the sampling rateswhich makes the three sampling frequencies close to each other.

Assume:

14

f_{s}^{1} < f_{s}^{2} < f_{s}^{3},

⌊\frac{f_{m a x}}{f_{s}^{3}}⌋ (f_{s}^{3} - f_{s}^{1}) \leq \frac{f_{s}^{1}}{2} .

Thus, the frequency upper bound is:

15

f_{m a x} = m i n \{f_{m a x 1}, (⌊\frac{f_{s}^{1}}{2 (f_{s}^{3} - f_{s}^{1})}⌋ + 1) f_{s}^{3}\} .

Then we have the following parameter combinations as shown in table 1according to Su [10] and each row represents a specific frequency region.

Table 1Reconstruction method

$f$	$p^{1}$	$p^{2}$	$p^{3}$	$q^{1}$	$q^{2}$	$q^{3}$
[0, $f_{s}^{1} / 2)$	0	0	0	1	1	1
[ $f_{s}^{1} / 2$ , $f_{s}^{2} / 2)$	0	0	1	1	1	–1
[ $f_{s}^{2} / 2$ , $f_{s}^{3} / 2)$	0	1	1	1	–1	–1
[ $f_{s}^{3} / 2$ , $f_{s}^{1})$	1	1	1	–1	–1	–1
[ $f_{s}^{1}$ , $f_{s}^{2})$	1	1	1	–1	–1	1
[ $f_{s}^{2}$ , $f_{s}^{3})$	1	1	1	–1	1	1
[ $f_{s}^{3}$ , ${3 f}_{s}^{1} / 2)$	1	1	1	1	1	1
[ ${3 f}_{s}^{1} / 2$ , ${3 f}_{s}^{2} / 2)$	1	1	2	1	1	–1
[ ${3 f}_{s}^{2} / 2$ , ${3 f}_{s}^{3} / 2)$	1	2	2	1	–1	–1
[ ${3 f}_{s}^{3} / 2$ , ${2 f}_{s}^{1})$	2	2	2	–1	–1	–1
…	…	…	…	…	…	…

We define the reconstruction loss function as:

16

f_{l o s s} = |(p^{1} f_{s}^{1} + q^{1} f_{r t}^{1}) - (p^{2} f_{s}^{2} + q^{2} f_{r t}^{2})| + |(p^{2} f_{s}^{2} + q^{2} f_{r t}^{2}) - (p^{3} f_{s}^{3} + q^{3} f_{r t}^{3})|

+ |(p^{1} f_{s}^{1} + q^{1} f_{r t}^{1}) - (p^{3} f_{s}^{3} + q^{3} f_{r t}^{3})| .

Then we can choose the best parameter combination with least $f_{l o s s}$ to reconstruct the signal frequency.

3. Simulation and results

We set the three sampling frequencies as1500 Hz, 1510 Hz and 1520 Hz. The maximum frequency which can be measured by our proposed estimator based on Eq. (15) is 57760 Hz. We can see that our estimator improves the upper bound of frequency measurement significantly.

Firstly, we test the performance of our estimator compared with Su [10]. We set the data length $N =$ 30 and signal frequency $f =$ 10000. In order to improve the speed of calculation, we construct a 5×5 autocorrelation matrix. If the data sequence with length greater than 5, we can construct multiple autocorrelation matrices using a sliding window with a length of 5and then compute the average matrix from them.

Fig. 2Estimator performance compared with Su [10]

The experiment result is shown in Fig. 2. We can see from the simulation result that our estimator not only has better accuracy at the high SNR region, but also is more resistant to noise. Su’s algorithm becomes unstable at 16 dB, while our algorithm starts to diverge at 10 dB.

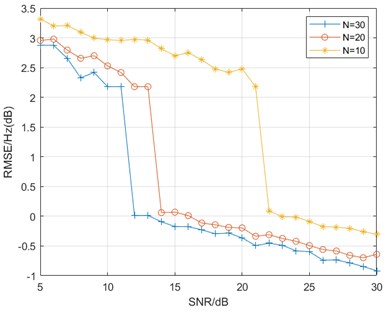
In addition, we also test the effect of the number of data points selected on the estimation accuracy. We still set to construct a 5×5 autocorrelation matrix, but the selected data lengths are 10, 20, and 30, and the other parameters are the same as in the previous experiment. Fig. 3 shows that the reconstruction accuracy improves as the number of data points increases, and the noise immunity also becomes stronger. However, it can also be found that the performance improvement gradually decreases as the number of points increases.

Fig. 3Estimator performance with different data lengths

4. Conclusions

To solve the single real-valued signal frequency estimation problem using ADC with a low sampling rate, we propose a multiple sub-Nyquist channel-based estimation algorithm. We first estimate the folded frequency of the signal based on the ESPRIT algorithm, and then use a search algorithm to reconstruct the signal frequency in the presence of constraints on the sampling frequencies. Experiments verify that our algorithm has good accuracy and noise immunity. Since the ESPRIT algorithm can handle multi-frequency estimation problems, it is a future research direction for us to improve the search algorithm to achieve multi-frequency reconstruction afterward.

References

S. Bhattacharya, T. Blumensath, B. Mulgrew, and M. Davies, “Fast encoding of synthetic aperture radar raw data using compressed sensing,” in 2007 IEEE/SP 14th Workshop on Statistical Signal Processing, p. 14, Aug. 2007, https://doi.org/10.1109/ssp.2007.4301298

Publisher
W. Bajwa, J. Haupt, A. Sayeed, and R. Nowak, “Compressive wireless sensing,” in The 5th International Conference, pp. 134–142, 2006, https://doi.org/10.1145/1127777.1127801

Publisher
Bin Le, T. W. Rondeau, J. H. Reed, and C. W. Bostian, “Analog-to-digital converters,” IEEE Signal Processing Magazine, Vol. 22, No. 6, pp. 69–77, Nov. 2005, https://doi.org/10.1109/msp.2005.1550190

Publisher
P. P. Vaidyanathan and P. Pal, “Sparse sensing with co-prime samplers and arrays,” IEEE Transactions on Signal Processing, Vol. 59, No. 2, pp. 573–586, Feb. 2011, https://doi.org/10.1109/tsp.2010.2089682

Publisher
X. Huang, Z. Yan, S. Jing, H. Fang, and L. Xiao, “Co-prime sensing-based frequency estimation using reduced single-tone snapshots,” Circuits, Systems, and Signal Processing, Vol. 35, No. 9, pp. 3355–3366, Sep. 2016, https://doi.org/10.1007/s00034-015-0193-3

Publisher
L. Xiao, X.-G. Xia, and W. Wang, “Multi-stage robust Chinese remainder theorem,” IEEE Transactions on Signal Processing, Vol. 62, No. 18, pp. 4772–4785, Sep. 2014, https://doi.org/10.1109/tsp.2014.2339798

Publisher
L. Xiao and X.-G. Xia, “A new robust Chinese remainder theorem with improved performance in frequency estimation from under sampled waveforms,” Signal Processing, Vol. 117, pp. 242–246, Dec. 2015, https://doi.org/10.1016/j.sigpro.2015.05.017

Publisher
X. Huang, H. Wang, H. Qin, and W. Nie, “Frequency estimator based on spectrum correction and remainder sifting for under sampled real-valued waveforms,” IEEE Access, Vol. 7, pp. 25980–25988, 2019, https://doi.org/10.1109/access.2019.2900284

Publisher
A. Maroosi and H. K. Bizaki, “Digital frequency determination of real waveforms based on multiple sensors with low sampling rates,” IEEE Sensors Journal, Vol. 12, No. 5, pp. 1483–1495, May 2012, https://doi.org/10.1109/jsen.2011.2173482

Publisher
Y. Su and D. Jiang, “Digital instantaneous frequency measurement of a real sinusoid based on three sub-nyquist sampling channels,” Mathematical Problems in Engineering, Vol. 2020, pp. 1–11, Mar. 2020, https://doi.org/10.1155/2020/5089761

Publisher
R. Roy and T. Kailath, “ESPRIT-estimation of signal parameters via rotational invariance techniques,” IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 37, No. 7, pp. 984–995, Jul. 1989, https://doi.org/10.1109/29.32276

Publisher

About this article

Received

28 July 2022

Accepted

07 August 2022

Published

25 August 2022

SUBJECTS

Dynamics and oscillations in electrical and electronics engineering

DOI

https://doi.org/10.21595/vp.2022.22835

Keywords

sub-Nyquist channel

ESPRIT

search-based

real-valued waveform

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 06 13

An instantaneous speed measurement method based on A/D acquisition method

Gaoquan Gu, Jing Zhang

Research article

2022 05 15

An adaptive beamforming algorithm for sound source localisation via hybrid compressive sensing reconstruction

Wenyong Guo, Jianggui Han, Hantao Chen, Li Yu, Zhe Wu

Research article

2021 11 05

Parameter identification of oscillations in power systems based on improved variational modal decomposition and HTLS-adaline method

Chunlu Wan, Kang Wang, Zhixiang Wu

Research article

2017 12 31

EEMD-Based cICA method for single-channel signal separation and fault feature extraction of gearbox

Junfa Leng, Shuangxi Jing, Chenxu Luo, Zhiyang Wang

L. Wang and S. Liu, “A new frequency estimation method for a real-valued waveform with multiple sub-Nyquist channels based on the ESPRIT algorithm,” Vibroengineering PROCEDIA, Vol. 44, pp. 71–76, Aug. 2022, https://doi.org/10.21595/vp.2022.22835

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22835
UR  - https://doi.org/10.21595/vp.2022.22835
TI  - A new frequency estimation method for a real-valued waveform with multiple sub-Nyquist channels based on the ESPRIT algorithm
T2  - Vibroengineering PROCEDIA
AU  - Wang, Lulu
AU  - Liu, Shang
PY  - 2022
DA  - 2022/08/25
PB  - JVE International Ltd.
SP  - 71-76
VL  - 44
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Wang_2022,
	doi = {10.21595/vp.2022.22835},
	url = {https://doi.org/10.21595/vp.2022.22835},
	year = 2022,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {44},
	pages = {71--76},
	author = {Lulu Wang and Shang Liu},
	title = {A new frequency estimation method for a real-valued waveform with multiple sub-Nyquist channels based on the {ESPRIT} algorithm},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]L. Wang and S. Liu, “A new frequency estimation method for a real-valued waveform with multiple sub-Nyquist channels based on the ESPRIT algorithm,” Vibroengineering PROCEDIA, vol. 44, pp. 71–76, Aug. 2022, doi: 10.21595/vp.2022.22835.

Copy IEEE

Copied to clipboard!

Wang, Lulu, and Shang Liu. “A New Frequency Estimation Method for a Real-Valued Waveform with Multiple Sub-Nyquist Channels Based on the ESPRIT Algorithm.” Vibroengineering PROCEDIA 44 (August 25, 2022): 71–76. https://doi.org/10.21595/vp.2022.22835.

Copy Chicago

Copied to clipboard!

A new frequency estimation method for a real-valued waveform with multiple sub-Nyquist channels based on the ESPRIT algorithm

Abstract

1. Introduction

2. Frequency estimator using multiple sub-Nyquist channels

2.1. Estimator overview

2.2. Obtaining folded frequency

2.3. Signal frequency reconstruction

3. Simulation and results

4. Conclusions

References

About this article

Related Articles