Study of horizontal aerodynamic force directed against a fluid flow at oscillations of elastically suspended plate

1. Introduction

It is known that the drag forces of vehicles are proportional to the square of their speed. For modern vehicles, due to their high speeds, this problem is quite acute. In this paper, an attempt is made to obtain the pulling force of an oscillating plate directed against motion. Then, for cars in the future, it is possible to create such systems with oscillating plates that will repeatedly reduce the resistance forces depending on the speed of movement. Research in this direction may prove promising for the transport industry, which may arouse the interest of oilmen.

In the article [1] it is shown that for a plate moving with translational velocity and oscillating according to some periodic law, there are modes in which the horizontal aerodynamic force applied to the plate pulls it forward. In this paper, the approach used in the works of V. A. Samsonov and D. V. Belyakov is adopted. Work [2] is devoted to the development of a mathematical model of self-oscillation of a plate in an air stream. Work [3] is devoted to the development of a mathematical model of the self-oscillations of an aerodynamic pendulum in the flow of the medium. As a model of the effect of the flow on the pendulum, a model of quasi-static flow around the plate by the medium is adopted. According to this hypothesis, the aerodynamic forces acting on the body are applied at the center of pressure. In the problem under consideration, the pressure center is movable relative to the plate. In [4], the equations of motion of a body in a medium flow and kinematic relations linking phase coordinates with the angle of attack are derived. The solution of the equilibrium equations is carried out and it is shown that the only equilibrium position is the state of rest. It is shown that as a result of interaction with the medium, the body in question can oscillate with increasing amplitude (flutter) in the flow of the medium. The paper [5] shows a violation of uniqueness in determining the angle of attack of an aerodynamic pendulum in a medium flow. A study of the stability of the equilibrium position corresponding to the state of rest, in which the Hurwitz criterion is implemented and the stability region is depicted, is carried out. It is shown that the forces of aerodynamic action for bodies with some shapes can contribute to the development of self-oscillations, and for others to attenuation. Work [6] and the study [7] are devoted to the construction and study of a mathematical model of the motion of an autorotating body of complex configuration in a gravitational field. Research is based on working with large databases. In [8], a systematic presentation of the problem of the motion of a material point and a solid body in a resisting medium is given. A consistent complication of the problem statement is carried out both with the enrichment of the environmental impact model and with an increase in the order of the dynamic system (from the first to the fourth). In [9], a qualitative analysis of the motion of a solid body in a resisting medium was carried out. In [10], a program is proposed that allows numerical studies of the stability of the rest state for the studied model of self-oscillations of the aerodynamic profile in the flow of the medium. The work [11] is devoted to the development of a mathematical model of a body of complex configuration that performs self-oscillations in the flow of a quasi-static medium under the action of aerodynamic forces. A violation of uniqueness in determining the angle of attack in some positions of the body has been established.

In the proposed work, the “plate-frame” system with two degrees of freedom is considered: it can rotate around the center of mass, which moves in a straight line. The restoring force and the restoring moment are directly proportional to the movements. The aerodynamic forces applied to the body are assumed in accordance with the empirical theory of stationary flow around a flat plate. It is assumed that the pressure center of the plate is movable and is located at some point A, the position of which is determined by the dependence of the distance to it from the center of mass of the plate, which is determined by blowing rectangular plates in the wind tunnel [12] and depends on the angle between the velocity of point A and the plate itself. The aerodynamic forces acting on the plate are decomposed into two components: the drag force directed against the velocity of point A relative to the flow of the medium, and the lifting force directed orthogonally to it.

In this article, for the first time, stable modes of plate oscillations with two degrees of freedom are numerically obtained, at which there is a pulling force directed against the flow of the medium, which was predicted by M.V. Keldysh. and Lavrentiev M. A. in the 40 s of the last century. The results obtained can be very useful for vehicles, since additional power is required to decreasing of aerodynamic drag forces for various types of vehicles, such as truck, airplane, train, ships and so on. It can lead to significant fuel economy.

2. Formulation of the problem

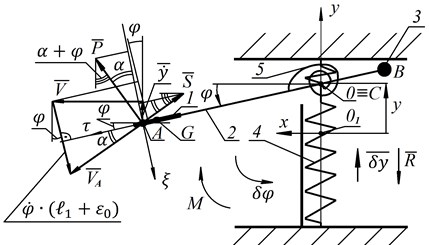
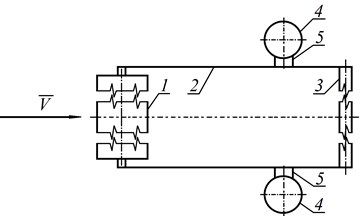
Fig. 1 shows plate 1 in a fluid (air) flow with the center of mass at point $G$. It is rigidly connected to the frame 2. The center of mass of the "plate-frame" system due to the counterweight 3 (point $B$) is at point $C$ (0). This point is connected to the fixed base by linear springs 4 and can move in a straight line. In addition, at this point the plate is connected to the torsion spring 5. A fixed coordinate system $x{0}_{1}y$ is used. A moving coordinate system $\tau 0\xi$ is rigidly connected to the plate. The plate at rest is in equilibrium and is oriented towards the flow. The restoring force and the restoring moment of springs 4 and 5 are directly proportional to the corresponding deviations:

The material of the plate is not important in this study, the plate is taken rigid and thin. Elongation, the ratio of the width of the plate to its length is assumed to be 8. The geometric dimensions of the plate are given in [12]. Self-oscillations of a plate with large amplitudes arising in a stationary air flow are investigated.

More detailed symbols and abbreviations are presented in the nomenclature.

Fig. 1A plate in a medium flow with two degrees of freedom: 1 – plate; 2 – frame; 3 – counterweight; 4 – linear springs; 5 – torsion spring

a) Front view

b) Top view

Fixed coordinate system $x{0}_{1}y$ and a movable coordinate system $\tau A\xi$, rigidly connected to the plate is introduced. In the resting position, the plate is in equilibrium and oriented towards the flow. Gravity forces are directed perpendicular to the drawing. The restoring force and the returning moment of springs 4 and 5 are directly proportional to the corresponding deviations: $R=-cy$; $M=-k\phi$.

The values of aerodynamic forces $\overrightarrow{S}$ and $\overrightarrow{P}$ acting at point $A$ are equal to:

where $\rho =$1,225 kg/m³ is the air density; $\sigma$ is the plate area; $\alpha$ – angle of attack between the vector $\overrightarrow{V_A}$ and the plate; $V_A$ is the velocity of point $A$ of the plate; $c_x\left(\alpha \right)$, $c_y\left(\alpha \right)$ – dimensionless aerodynamic functions (Fig. 1(a)).

Velocity of point $A$:

Projection of the velocity vector to $x$-axis:

Projection of the velocity vector to $y$-axis:

The form of aerodynamic functions for different shapes of plates is given in [12]. The schemes in cases of Fig. 2(a) and Fig. 2(b) show such dependences for a plate with elongation. These dependences are approximated in the first order by the analytical functions (case Fig. 2(c) and Fig. 2(d)).

Fig. 2Dimensionless aerodynamic functions cxα and cyα

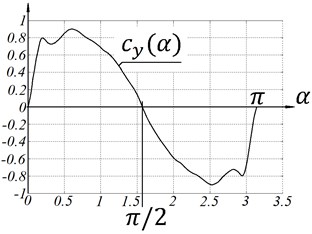
a) Case “A”

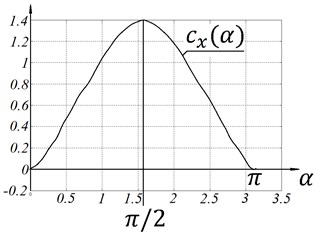
b) Case “B”

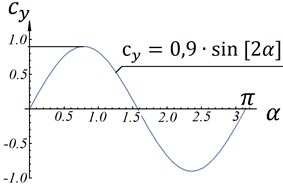
a) Case “C”

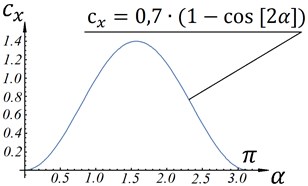
b) Case “D”

The velocity of point $A$ is determined as the sum of three vectors (Fig. 1(a)):

where $\dot{y}$ is the velocity of point 0; V is the air flow rate; $\dot{\phi }$ is the angular velocity of the plate; $A0=0G+GA$.

Let $0G={\mathcal{l}}_1$ be the distance between the center of mass of the “plate-frame” system to the center of mass of the plate.

The pressure center of the plate, point A, is considered to be mobile, and the distance GA is described by the dependence $\epsilon \left(\alpha \right)$, which is determined from blowing rectangular plates with a given elongation in a wind tunnel and is experimental data [12]. To determine the angle $\alpha$, we determine the tangent of this angle by projecting the components of the vector $\overrightarrow{V_A}$(2) on the axis $\xi$ and $\tau$. We accept the change in the projection on the $\epsilon \left(\alpha \right)$$x$-axis during plate vibrations as insignificant in relation to the value ${\mathcal{l}}_1$ and consider that $\epsilon \left(\alpha \right)\equiv {\epsilon }_0-const$:

The scheme in Fig. 1 was chosen from the condition of simplifying calculations. With such a scheme, to determine the angle $\alpha$, a numerical solution of Eq. (3) is not required (if ${\epsilon }_0$ the function would be instead $\epsilon \left(\alpha \right)$) and Eq. (4) can be used:

The system in Fig. 1 has two degrees of freedom. Let us write the Lagrange equation of the second kind for the coordinates $y$ and $\phi$:

where $T$ is the kinetic energy; $Q_{\delta y}$, $Q_{\delta \phi }$ are the generalized forces in the corresponding coordinates.

The kinetic energy of the system is determined by the following formula:

where $m$ is the mass of the plate and the frame (Fig. 1, mass of the springs is neglected); $I_C$ is the moment of inertia of the "plate-frame" system relative to its center of mass; $V_C=\dot{y}$ is the velocity of the center of mass of the “plate-frame” system.

To determine the generalized forces $Q_{\delta y}$ and, $Q_{\delta \phi }$ we equate the corresponding variations $\delta \phi$ and to zero $\delta y$. Then:

Finally, we obtain the following differential equations describing the oscillations of the system in Fig. 1:

The initial conditions of Eq. (7) are as follows: At $t=$0: $y_0={\phi }_0=0$; ${\dot{y}}_0>0$; ${\dot{\phi }}_0>0$.

The system of differential Eq. (7) was solved numerically in the Wolfram Mathematica mathematical package.

3. Oscillation analysis

We project the aerodynamic forces $\overrightarrow{P}$ and $\overrightarrow{S}$ acting on the plate on the $x$-axis (Fig. 1):

Analysis of solutions of differential Eq. (7) showed that there are stable modes of oscillations (frequency and amplitude of oscillations do not change with time) of the system in Fig. 1 in which the horizontal aerodynamic force $Q$ is directed against the oncoming flow (Fig. 3 (a)). Due to the incommensurability of the magnitude $Q$ and the magnitudes $y$ and $\phi$, the dependencies 1000$Q$ and 0.01$Q$ are presented in Fig. 3 for clarity. If the flow velocity is $V=$ 89 m/s then oscillations qualitatively change their form, and the horizontal force $Q$ becomes negative (Fig. 3(b)). As can be seen from Fig. 3(b), the absolute value of force $Q$ increases by several orders of magnitude. For a case Fig. 3(a) the angle $\alpha$ according to Eq. (4) is almost equal to 0 (it changes from –3∙10^-6 to 3∙10^-6 rad.). For a case Fig. 3 (b), the angle $\alpha$ also remains almost constant with time and equals approximately –0.133 rad.

Fig. 3Dependences of coordinates y, φ and horizontal aerodynamic force Q relative to time: σ= 0.2 m2; ε0= 0.3 m; l1= 2 m; m= 19.2 kg; I0= 19,8 kg∙m2; c= 3870 N∙m/rad; k= 3990 N/m; y0=φ0= 0; y˙0= 1 m/s; φ˙0= 1 s-1

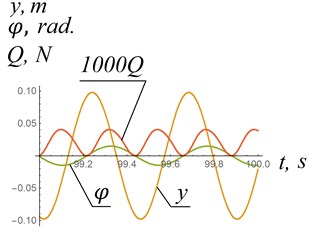
a) Behavior of the system in a case of $\mathrm{V}=$ 88 m/s

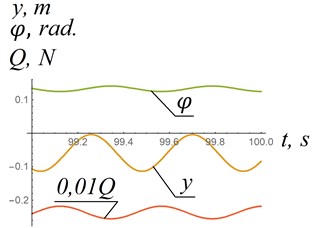
b) Change in behavior of the system in a case of $\mathrm{V}=$ 89 m/s

With a further increase in the velocity $V$, the practically constant angle $\alpha$ decreases. For example, at $V=$ 100 m/s $\alpha \approx$–0.82 rad. At $V>$ 127 m/s the numerical solution of Eq. (7) failed, the coordinates $y$ and $\phi$ tend to infinity. The nature of this failure is not clear at the moment. Additional research on this topic is required.

The natural frequencies of the “plate-frame” system (Fig. 1) for the case shown in Fig. 3(a) are as follows: $p_1=\sqrt{c/m}\approx$14.1973 s^-1; $p_2=\sqrt{k/I_0}\approx$14.1956 s^-1. At these frequencies, the oscillations are steady. When these natural frequencies change, the vibrations of the plate, at which there is a “pulling” force directed against the flow, disappear. With certain parameters of the system in Fig. 1, resonance is possible ($Q<$ 0 (Fig. 4(a)). Also damped oscillations are possible ($Q<$ 0, Fig. 4(b)).

Fig. 4Dependences of coordinates y, φ relative to time: σ= 0.2 m2; ε0= 0.3 m; l1= 2 m; V= 20 m/s; I0= 5 kg∙m2; c= 3870 N∙m/rad; k= 3990 N/m; y0=φ0= 0; y˙0= 1 m/s; φ˙0= 1 s-1

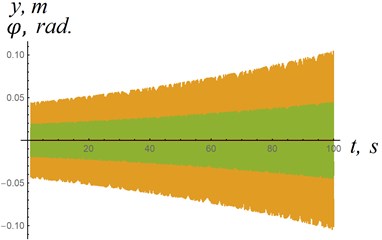
a) Resonance in the system in a case $m=$ 5 kg

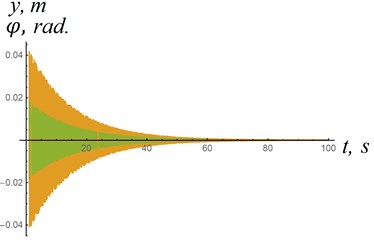
b) Damped oscillations in the system $m=$ 5.5 kg

4. Conclusions

In conclusions two main theses can be underlines.

The first thesis: within the framework of the proposed mathematical model, there are stable oscillation modes of the considered system with two degrees of freedom, in which the horizontal aerodynamic force acting on the plate is directed against the oncoming flow.

The second thesis: in the proposed mathematical model resonance and damped oscillations are possible.

The third thesis: there are stable modes of oscillation, in which the angles of attack between the velocity vector of the center of pressure of the plate and the plate itself are practically constant.