Abstract
The structural seismic performance of steel frame-precast steel reinforced concrete (SRC) infill wall with lateral force resisting is analyzed, and the structural strength of steel frame-precast SRC infill wall with lateral force resisting is improved. The structural seismic performance optimization model of SRC lateral force resisting wall based on buckling restrained brace is proposed. Through the finite element simulation software, the seismic performance and response results of ordinary steel frames, buckling restrained braced steel frames and a relatively new type of sacrificial-energy dissipation braced steel frames under earthquake are compared and analyzed to demonstrate the applicability and performance advantages of sacrificial-energy dissipation braced steel frames in the steel frame braced structure system. Under the action of horizontal earthquake, the supporting members experience reciprocating axial tension and compression cycles, which dissipate a large amount of seismic energy input into the structure. Therefore, the buckling restraint support method can be used in the structure to improve the support strength. Under horizontal reciprocating load action of earthquake, the ability to consume seismic energy through self-hysteresis of the brace is poor. Experimental research shows that, the unbalanced force formed in the beam of the frame beam under seismic action will form a plastic hinge at the beam end at both ends of the frame beam. Especially when the brace is buckling unstable and the stiffness of the frame beam is small, the plastic hinge effect at the beam end is significant. This phenomenon may cause damage to the frame beam or even local floor subsidence. The buckling restraint support has a full hysteresis area under axial tension and compression, and its mechanical performance is excellent. It is obviously superior to ordinary steel bracing in energy dissipation capacity and seismic performance. It can accurately predict the bearing capacity of reinforced concrete under strong earthquake, and the energy dissipation distribution is more in line with the requirements of “energy seismic design method”.
1. Introduction
Earthquake is a common sudden natural disaster, which has a wide range of disasters and is destructive. At the current scientific level, the occurrence of earthquakes and the characteristics of ground motions are unpredictable. Once they break out, they will bring very serious losses to human beings. Therefore, earthquakes are also one of the most serious natural disasters facing human beings, and have been accompanied by the survival and development of human society since ancient times. Earthquake is divided into tectonic earthquake, volcanic earthquake, subsidence earthquake and induced earthquake. Among them, tectonic earthquake is the most frequent and destructive earthquake since records. Steel structure buildings have shown good anti-seismic ability in previous earthquake disasters, but also exposed some problems and defects. For example, in steel frame structures, the members have strong deformation capacity and good ductility, but the structure itself has insufficient lateral stiffness, and beams, columns and other members enter into yield under earthquake action, resulting in excessive deformation. Therefore, the horizontal lateral stiffness of steel frame structure can be effectively increased by setting supporting members, so that the advantages of applying steel frame-bracing structure in seismic fortification areas can be reflected.
Steel frame is a typical flexible structural system, and frame columns are the main lateral force resisting members in frame structures. However, under earthquake action, its lateral stiffness is usually difficult to resist horizontal seismic forces, which makes the overall structure produce large lateral displacement. In order to meet the inter-story displacement angle limit and lateral stiffness requirements in engineering design, it is a common method to increase the section size of related members. However, this not only increases the use of materials, but also improves the weight of the structure and the project cost. On the other hand, the increase of the lateral stiffness of the structure after the increase of the cross-sectional area of the frame column will instead lead to the structure absorbing more energy under the earthquake action, and finally fall into the adverse cycle of increasing the member stiffness due to insufficient lateral stiffness and increasing the member stiffness resulting in increased seismic action.
Therefore, it is necessary to set support members between the beam and column nodes of the steel frame to improve the horizontal lateral stiffness. The steel frame that does not produce eccentric intersection between the support itself and the frame beam and the frame column is called the center supported steel frame. Bracing can be roughly divided into three types: ordinary bracing, buckling restrained bracing, and sacrificial-energy dissipation bracing. Each type of bracing inherits the advantages of the former and improves the disadvantages of the former. With the continuous progress of urbanization, the development of modern urban buildings is moving towards high-rise reinforced concrete frame structures. Today, concrete is widely used in the design of building materials. Concrete is a composite material composed of coarse and fine aggregates, cement hydrates and pores. Based on concrete, it is used to build a high-rise reinforced concrete frame structure building. The research on the seismic strength and seismic performance of high-rise buildings with reinforced concrete as the main body has always been the focus of building structure and building theory research. Under the strong earthquake load, the sway response of the push-pull lateral eccentric structure of the reinforced concrete frame beam-column structure appears, and the seismic model of the sway response of the reinforced concrete eccentric structure under the strong earthquake load is studied to improve the seismic strength of the reinforced concrete. According to the requirements of the Code for Seismic Design of Building Structures, it is of great significance to study the shaking response seismic model of reinforced concrete building structures in the analysis of building structures [1].
Under the action of frequent earthquakes, the ordinary bracing is kept in an elastic state. Under the elastic state, it can better maintain its own strength and stiffness, reduce the horizontal displacement of the structure to some extent, and optimize the internal force transmission and energy distribution of the structure. However, steel frame braced structures with ordinary braces are prone to compression buckling due to repeated tension and compression under earthquake action. Therefore, the energy dissipation performance of ordinary braces is relatively low. Repeated buckling will lead to local structure damage and overall structure earthquake damage, and ultimately reduce the bearing capacity and safety of the structure. In the traditional method, the research on the seismic model of eccentric structure of reinforced concrete frame beam-column structure mainly adopts the mathematical model of beam-column element. The method of stirrup and transverse connection reinforcement load reinforcement is used to carry out seismic reinforcement and seismic parameter design, which has achieved a certain seismic effect. With the frequent occurrence of large earthquakes in recent years, the research on the seismic model of reinforced concrete buildings has attracted people's attention [2]. Reference [3] established a shaking response seismic model based on linear beam-column element mathematical model and transverse reinforcement yield mechanism, analyzed the internal force redistribution and energy consumption curve of structure of steel frame-precast steel reinforced concrete (SRC) infill wall with lateral force resisting, and improved the seismic strength of the building structure. However, the residual bearing capacity estimation accuracy of the model for concrete eccentric structure is not high, and the seismic strength prediction accuracy is not good; Reference [4] proposed a design scheme of shaking response seismic model for reinforced concrete testing of single-row and double-row connection plane rotation rigid body, obtained the evaluation coefficient of yield mechanism, and achieved seismic optimization. However, the model at the same load level, due to the use of discrete prediction method, the numerical evaluation results of residual tensile strength are not accurate.
Through the finite element simulation software, this paper compares and analyzes the seismic performance and response results of ordinary steel frames, buckling restrained braced steel frames and a relatively new type of sacrificial energy-dissipation braced steel frames under earthquake action, to demonstrate the applicability and performance advantages of sacrificial energy-dissipation braced steel frames in the steel frame-braced structure system, hoping to help the actual engineering construction. Braced members experience reciprocating axial tension and compression cycles under horizontal earthquake action, which dissipates a large amount of seismic energy input into the structure. Therefore, buckling restrained bracing can be used in the structure to improve the support strength. Under horizontal reciprocating load action of earthquake, the ability to consume seismic energy through self-hysteresis of the brace is poor. Experimental research shows that, the unbalanced force formed in the beam of the frame beam under the earthquake action will form a plastic hinge at the beam end at both ends of the frame beam. In this paper, an improved seismic model of shaking response of reinforced concrete eccentric structure under strong earthquake load is designed. Firstly, the mechanical analysis model for the structure of steel frame-precast steel reinforced concrete (SRC) infill wall with lateral force resisting is constructed, and the structural mechanical analysis test design of reinforced concrete eccentric structure under strong earthquake load is carried out, to realize the improvement of seismic model under shaking response, which can effectively guide the seismic design and structural optimization of reinforced concrete shock absorption walls in high-rise buildings.
2. Mechanical analysis model of structure of steel frame-precast steel reinforced concrete (SRC) infill wall with lateral force resisting
2.1. Problem description and design principle
In this paper, the seismic model of eccentric structure of reinforced concrete frame beam-column structure is studied. Firstly, the finite element modeling of high-rise building is carried out. Before modeling, several principles of seismic model design are described. Under strong earthquake load, the seismic optimization of push over lateral eccentric structure of reinforced concrete frame beam-column structure should follow the following principles:
(1) In building seismic input, it can analyze the weak floors of the original building, and try not to transfer them. If they are transferred, new weak floors will be generated. When external factors occur, disasters cannot be prevented and controlled;
(2) In the optimization ratio of building seismic input and impact resistance, the needs of building use should be comprehensively considered, which should not only pursue the improvement of building performance, but also consider the cost control and impact resistance use of the building body;
(3) When the new support points are used for the seismic design of buildings, the seismic redistribution and stress of the system shall be considered.
Bracing is the first line of defense in the two lines of defense of lateral force resisting system, which bears most of the earthquake action compared with frame beams, frame columns and other components under the earthquake action. Under the horizontal earthquake action, the supporting members experience reciprocating axial tension and compression cycles, which dissipate a large amount of seismic energy input into the structure, so they can play the role of energy dissipation and vibration reduction in the structure, ensuring that the frame column and frame beam will not be damaged under the greater earthquake action. At the same time, under the action of strong earthquake, some lateral force resisting members of the structure will also be partially destroyed under strong earthquake, which makes the seismic action borne by the whole structure decrease with the decrease of the overall stiffness of the structure. Therefore, compared with bracing, the frame part composed of frame beam and frame column bears less residual seismic force, which avoids local serious damage or overall collapse of the structure under strong earthquake.
2.2. Finite element model of the structure of precast SRC wall with lateral force resisting
According to the above design principles, the shaking response seismic model design of reinforced concrete under strong earthquake load is carried out. The seismic material grades of reinforced concrete buildings are divided into four strength grades: C70, C60, C50 and C40. The coordinate system of the model is set as , where the axis is 50 m and the axis is 40 m. During the earthquake, the force transmitted by the building block is mainly borne by the horizontal tie bar on the upper surface of the bent cap/abutment cap. In the test, the sampling frequency of the data acquisition system is 1000 Hz, the MAXWELL seismic strong connection unit is used, and the coordinate system of the steel concrete structure model under the strong seismic load is set as , where the axis is 50 m, the axis is 40 m, and the seismic strength grade of the steel pipe and steel beam is Q345. In the design of high-rise buildings, the building structure studied in this paper is 60 floors, the height of ground floor is 5.4 m, and the 1~20 floors are the strength grade of the internal and external layers of the C60 wall structure, Floors 21~35 are C70 seismic strength grade. Based on the above description, the simulation analysis of the post-earthquake buckling relationship of steel reinforced concrete and the yield field effect of the specimen structure are analyzed, the mesh division of the concrete elastoplastic model and the boundary condition analysis are carried out, and the finite element model of the reinforced concrete eccentric structure under the strong earthquake load is obtained by using MAXWELL strong damping connection element and combining with the finite element analysis software, as shown in Fig. 1.
Fig. 1Finite element model of reinforced concrete eccentric structure under strong earthquake load
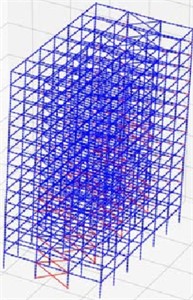
a) SED support steel frame
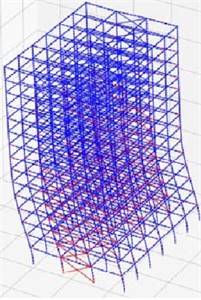
b) BRB steel frame
In Fig. 1, considering the influence of high temperature creep and transient thermal strain on the residual pushover lateral bearing capacity of reinforced concrete, the relationship between the mechanical properties of reinforced concrete, temperature and load during the post earthquake buckling relationship simulation of steel reinforced concrete is obtained.
However, under the horizontal reciprocating load of the earthquake, the internal force of the ordinary steel support changes repeatedly under the axial tension and axial compression, resulting in compression buckling. The whole structure loses the first line of defense against the earthquake after its buckling (the bearing capacity and stiffness of the support are significantly reduced). At the same time, the hysteretic curve shape of ordinary steel support under horizontal reciprocating load is not full, and its ability to consume seismic energy through supporting its own hysteretic is poor, so it cannot fully absorb the energy of ground motion after yielding under strong earthquake.
The influence of seismic sloshing response on the seismic performance index of SRCSSC-SB side node under strong earthquake is shown in Fig. 2.
Fig. 2Influence relationship of seismic performance indexes of SRCSSC-SB side joints
The same form of steel distribution is used to complete the segmentation of the three-dimensional nodes of the side columns in the middle layer of the special-shaped column frame. In the simplified positive overpressure pulse load part, the time history curve is simplified into two hypothetical triangular loads, and the load wave reduces to zero after a period of time (positive overpressure), thus generating positive overpressure pulse load and negative overpressure pulse load.
Through the above design, the shaking response finite element modeling of reinforced concrete eccentric structure under strong earthquake load is obtained, which lays the foundation for seismic model setting.
2.3. Mechanical analysis of concrete strength structure under strong earthquake load
On the basis of the above model framework, the mechanical analysis of concrete strength structure under strong earthquake load is carried out, and the solid phase extraction method is used to analyze the solid phase adsorption layer of structural members under the splitting load. The adsorption splitting load makes the response and failure of the building structure present certain probability characteristics. In order to accurately analyze the overpressure load model of steel beam building structure under the splitting load, the definitions of the following parameters are given: arrival time of seismic wave front , peak to peak value of positive overpressure pulse load , and the elastic modulus of transverse reinforcement of concrete mixture is expressed as:
where, and represent the static and residual tensile strength of the residual tensile strength of steel reinforced concrete after the earthquake, respectively, and , , and represent the weight coefficient proportion of each energy item in the process of concrete cracking, longitudinal reinforcement yielding, and concrete protection, all of which are constants greater than 0. The measured damage state of concrete eccentric structure under strong earthquake is linked with the engineering limit state, and the expressions of the reinforcement section area and the concrete section area are obtained as follows:
where, refers to the proportion of the bearing capacity of the building beam in the whole tensile strength force field analysis of concrete, and refers to the overall sectional area of the eccentric structure under strong earthquake load. According to the above structural mechanics analysis relationship, the general software PKPM is used for structural design. The constraint function relationship of load control reinforcement between different seismic strengths and of high-rise frame buildings is as follows:
where, represents the displacement increment of reinforced concrete section steel after yielding, represents the ultimate bearing capacity, and represents the horizontal loading load. Based on the measured hysteresis curve, the distribution relationship of the internal force of the reinforced concrete specimen section under the ultimate load in the seismic load is obtained as follows:
According to the Euler-Bernoulli beam theory, the distribution model for the longitudinal residual stress of the impact resistance of the reinforced concrete under the ultimate load is obtained, and the structural mechanics analysis of the reinforced concrete of the steel structure building under the strong seismic load is realized, based on which the seismic model is analyzed. The horizontal lateral force in the steel frame structure is mainly borne by the steel brace. The vertical bearing capacity of the main structure will not be reduced due to the yielding of the brace. Generally, the brace is more sensitive to the lateral deformation than the frame column, frame beam and other components under the horizontal seismic action. Therefore, the brace, as the main energy dissipation component in the structure, will yield first than the beam and column components under the seismic action. If appropriate supports can be adopted, so that more energy can be consumed by the supports under a given structure, more energy can be absorbed by the secondary structure, so as to reduce the damage of the main structure and protect the main structure under the earthquake. Finally, the energy based seismic design method can be embodied from the construction level.
3. Test overview
3.1. Specimen structure and loading method
According to the above theoretical analysis, the anti-seismic model test design of reinforced concrete under strong earthquake load is carried out. The test specimen structure is selected as the steel distribution form of column section, the reinforced concrete structure form of horizontal load and column section, and the distance between column bending points is 1600 mm. In order to accurately simulate the load and tensile strength of nodes under actual earthquake, the anti-seismic layer section of strong concrete under earthquake action is H300 mm×150 mm×6 mm×10 mm, the thickness of concrete cover is 20 mm, the loading strength of concrete column ends distributed transversely is 45 N/mm2, and the middle reinforcement of concrete is ϕ6@200. In order to accurately simulate the stress performance under earthquake, the loading profile of reinforced concrete specimen under strong earthquake load is shown in Fig. 3. The test specimen of the sacrificial section adopts Q345 square steel pipe with a thickness of 25 mm in the form of outer three side enclosure to ensure that the mechanical properties of the sacrificial section are consistent under tension and compression. The square steel pipe and the fixed end of the sacrificial section are connected by means of bolt connection (bolted connection plate in Fig. 3(a)). Shear failure of the connecting bolts in the bolted connection plate is the main means to control the sacrifice of the sacrificial section. In order to meet the requirement that the tensile bearing capacity of the sacrificial section of the square steel pipe is far greater than the shear bearing capacity of the bolt, the test uses two bolts to form a bolted connection plate, and its shear bearing capacity is calibrated through the test. The energy consuming section shall meet the requirements of continuous and efficient energy consumption after the sacrificial section is out of service. Therefore, the energy consuming section adopts LY225 steel as its core plate material, which is a buckling resistant support with excellent energy dissipation performance. In the subsequent study, the strength of sacrificial section and energy dissipation section can be achieved by modifying their corresponding section parameters and material strength.
Fig. 3Loading profile of reinforced concrete specimen under strong earthquake load

a) Reinforced concrete specimen loading frame diagram

b) Sacrificial energy-dissipation support specimen loading device
The mathematical model of initial damage and free degradation of concrete material after earthquake is established, and the elastic modulus of concrete mixture is obtained. The numerical analysis results of the residual tensile strength of the steel reinforced concrete buckling relationship after earthquake are obtained from the perspective of test analysis. In the load control stage, a statistical model of the splitting load is obtained by taking 5 kN as the load step. Based on this model, 77 groups of data measured from the splitting test are combined to form a splitting load database, and the average value, standard deviation and variation coefficient of each parameter of the splitting load at different proportional distances are obtained.
The damage figure of bolt connecting plate obtained by the test is shown in Fig. 4. The test hysteresis curve is positive under pressure and negative under tension. Before the specimen reaches the peak bearing capacity, the sacrificial section and the energy dissipation section work together. When the specimen is compressed, the peak bearing capacity is 789 kN, and the displacement of the specimen is 2.45 mm; When the specimen is in tension, the peak bearing capacity is 865 kN, and the displacement of the specimen is 2.45 mm. After reaching the peak bearing capacity, the hysteresis curve enters the descending section, that is, the upper bolt and the lower bolt have shear failure successively in the first circle of 3 mm and the second circle of 3 mm, the bolt falls down and exits the work (as shown in Fig. 4(a) and 4(b)), and the sacrificial section exits from the stress.
Fig. 4Damage diagram of bolt connecting plate

a) Damage of upper bolt

b) Damage of lower bolts
According to curve fitting, the parameters of pushover lateral bearing strength of reinforced concrete eccentric structure under strong earthquake load are shown in Table 1.
Table 1Parameters of push over lateral bearing strength of reinforced concrete eccentric structures under strong seismic loads
Model | Characteristic period / s | Ultimate bearing capacity / (kN) | Lateral unloading / kPa |
HA250×250 | 60.418 | 41.735 | 109.314 |
HA300×200 | 67.701 | 39.929 | 114.857 |
HA350×250 | 68.491 | 45.576 | 115.225 |
HA400×200 | 60.783 | 35.725 | 109.176 |
HA300×250 | 65.340 | 49.828 | 116.877 |
HA500×200 | 63.908 | 41.358 | 119.946 |
HA300×300 | 64.956 | 49.648 | 106.006 |
Combined with the parameter settings given in Table 1, in the seismic model design and test, the load-displacement dual control loading system is adopted. The horizontal loading under strong earthquake is divided into two stages: load control and displacement control. The incremental decomposition of displacement and cyclic loading simulation are carried out. The mathematical analysis of the index parameters of seismic performance is carried out by using the column end loading method, until the load drops to 85 % of the limit value. The sloshing response coefficient in earthquake is calculated, and the seismic wave loads along different directions of beams in three directions are obtained through test acquisition, so as to realize the linear behavior simulation of sloshing response of reinforced concrete under seismic load. At this time, only BRB in the member as the energy dissipation section continues to work, and then the compression bearing capacity of the test piece decreases to 402 kN, and the tensile bearing capacity decreases to 384 kN, so the average strength of the energy dissipation section is 393 kN, the average strength of the sacrificial section is 434k N, and the strength ratio of the sacrificial section and the energy dissipation section is 5.3:4.7. When the load reaches 22 kN/m2, the core area of the energy consuming section is obviously deformed and the load is stopped. The descending section of the hysteresis curve is obvious. In the later stage, only the energy consuming section is in full shape. The energy consuming section using BRB has good ductility and strong deformation capacity, so the energy dissipation effect of the sacrificial energy dissipation brace is good. In the later research, by adjusting the shear strength of the shear bolt of the bolted connection plate, as well as the parameters such as the material and section of the energy dissipation section, the peak load of the sacrificial section after it exits the work and the strength of the energy dissipation section after it exits the work can be controlled, which is used to study the optimal proportion of the sacrificial section and the energy dissipation section of the sacrificial energy dissipation support in the steel frame support structure.
3.2. Seismic strength analysis test
Under the above test device and test component loading mode, the seismic strength analysis test of reinforced concrete shaking response failure mode under strong earthquake load is carried out. This paper analyzes the eccentric structure model under strong earthquake action of reinforced concrete, arranges 4 longitudinal bars with diameter of 16 mm, stirrup spacing of 150 mm, and conducts simulated earthquake impact test. Through the simulated earthquake impact test, the finite element simulation of shaking response is realized. The damage process of test group members under strong earthquake load is shown in Fig. 5.
Fig. 5Concrete damage process under strong earthquake load

It can be seen from Fig. 5 that under strong earthquake load, concrete fragments are splashed around the column, generating eccentric process and shaking response, and sudden crushing brittle failure occurs. According to the Code for Seismic Design of Building Structures (GB50011-2010), a yield mechanism of strong column and weak beam is built, and pushover analysis and elastic-plastic time history analysis are carried out for concrete structures under strong earthquake load. According to the 10 storey frame beam-column element model structure, the stiffness method is used to simulate the yield surface constitutive relationship under sloshing response at the section level, and the axial force expression of the structural pushover section is obtained as follows:
The constitutive relationship of yield surface under sloshing response is simulated, and the axial force expression of structural pushover section is obtained as follows:
where, represents the incremental constitutive deformation of the concrete bending yield surface under strong earthquake load, and represents the spatial strength of the internal force of the section hierarchy. The assessment coefficient of integral yield mechanism for the structure of steel frame-precast SRC infill wall with lateral force resisting under strong earthquake load is obtained:
where, represents the lateral bearing capacity of the nappe, and represents the peak displacement of the characteristic period of the sloshing response. Under the strong earthquake load, the eccentricity of the concrete is calculated, and the maximum interlayer displacement is:
where, is the number of integral sections. Through the above analysis, considering the seismic input of SSI effect, the seismic analysis model of shaking response of reinforced concrete eccentric structures with integral yield mechanism under strong earthquakes is obtained.
4. Numerical analysis of test results
According to the above test description and test component loading, the Truss Element in Openses is used to model the sacrificial energy dissipation support. The Truss Element in Openses defaults to hinge at both ends, which corresponds to the hinge connection between the support and the beam-column node in the frame support structure, and does not include any nonlinearity, meeting the stress and deformation characteristics of BRB when the energy dissipation section continues to work. Therefore, it can better simulate and reflect the mechanical performance of the sacrificial-energy dissipation brace in the frame-brace structure. The shaking response seismic analysis test of reinforced concrete eccentric structure under strong earthquake load is conducted. The calculation simulation method is adopted. The section NM coupling element and finite element model element are used for modeling. The Truss Element and Steel02 Material in Openses are used for modeling BRB. Steel02 Material is used to construct the uniaxial Giuffre Menegotto Pinto steel hysteretic constitutive model with isotropic strain and hardening (MP model constitutive model). The design seismic intensity is 8 degrees, and the seismic strength analysis structure is derived by referring to PKPM program after comparing the impact of each seismic performance index of SRCSSC-SB side node. Under the environmental conditions of Class III and IV, the seismic performance of the reinforced structure is designed. The 3-story, 6-story, 8-story and 10-story reinforced concrete eccentric structure frame structures are designed with PKPM software. The seismic wave is shown in Fig. 6.
Fig. 6Seismic wave
a) RSN-67
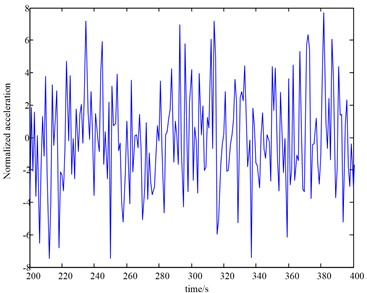
b) RSN-76
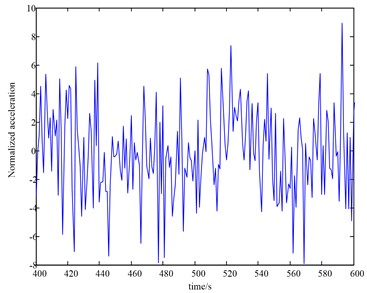
c) RSN-95
Since the ground motion is a random process, the acceleration time history curves recorded at the same place with the same ground motion intensity are quite different, and different ground motion acceleration time history curves correspond to different response spectrum curves. The dynamic characteristics of the earthquake occurring at the site where the building is located are unpredictable due to its sudden and accidental nature. Therefore, in the seismic design of building structures, the response spectrum curve corresponding to each ground motion acceleration time history curve must be solved by referring to the ground motion acceleration time history obtained during strong earthquakes on the same type of site. After selecting 7 seismic waves, it can calculate the average response spectrum of the selected ground motion to verify that the mean absolute acceleration response spectrum of the ground motion is statistically consistent with the design response spectrum curve. The peak value, mean value, standard deviation, coefficient of variation and proportional distance relationship curve of the pushover lateral bearing capacity of reinforced concrete integral yield mechanism under strong earthquake load are obtained as shown in Fig. 7.
Fig. 7Relation curve of nappe variation under strong earthquake load
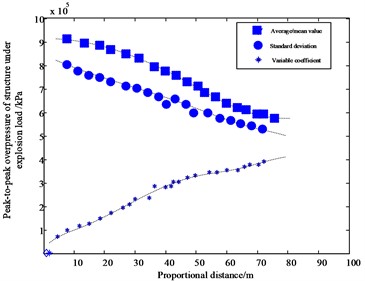
Fig. 7 shows the fitting curve of the mean value, standard deviation, variation coefficient and proportional distance obtained by the least square method. Through the analysis of the fitting curve, it is found that the average value and standard deviation of the building structure under strong earthquake are well fitted, and the regression coefficient of the variation coefficient is only 0.573. It can be seen that the seismic model designed in this paper can be used to estimate the lateral bearing capacity of the nappe under strong earthquake load, and thus improve the seismic performance of reinforced concrete building structures. According to the above test results, the least square approximation method is used to analyze the relationship between the nappe lateral bearing capacity of sloshing response under strong earthquake load and the displacement of the building structure at the fixed point. The test results are shown in Fig. 8.
Fig. 8Double estimation results for the structural seismic force of steel frame-precast SRC wall with lateral force resisting
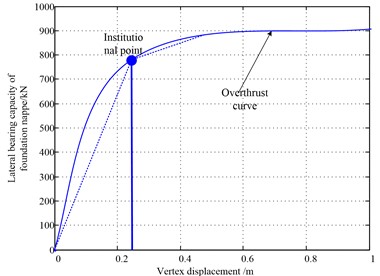
Based on the double estimation results for the seismic capacity of the structural seismic force of steel frame-precast SRC wall with lateral force resisting given in Fig. 8, a discrete estimation model of the pushover lateral bearing capacity under strong earthquakes is obtained. The simulation analysis of the post-earthquake buckling relationship of steel reinforced concrete and the yield field effect of the specimen structure are analyzed, and the test results are shown in Table 2.
Table 2Seismic mechanical test results of the structure of steel frame-precast SRC infill wall with lateral force resisting
Node No. | Vertical displacement of top floor / m | Support / t | Error / % |
421 | 42.760 | 0.845 | 0.230 |
422 | 47.152 | 0.268 | 0.753 |
423 | 40.349 | 0.926 | 0.028 |
424 | 49.728 | 0.204 | 0.588 |
425 | 42.917 | 0.996 | 0.187 |
426 | 45.428 | 0.713 | 0.530 |
427 | 40.828 | 0.982 | 0.678 |
428 | 45.945 | 0.281 | 0.379 |
429 | 41.244 | 0.127 | 0.749 |
430 | 42.172 | 0.524 | 0.225 |
431 | 43.054 | 0.065 | 0.944 |
432 | 45.820 | 0.302 | 0.950 |
Mesh generation and boundary condition analysis of concrete elastoplastic model are carried out, and the bearing strength of 3-story, 6-story, 8-story and 10-story reinforced concrete eccentric structural frame structures under strong earthquake is calculated, as shown in Fig. 9.
Fig. 9Calculation of bearing strength
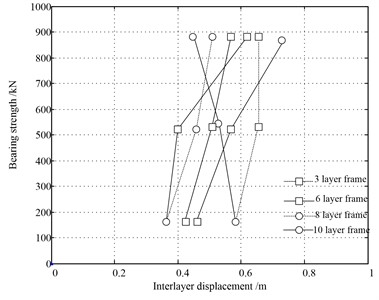
By analyzing the above test results, it can be seen that the reinforced concrete seismic model designed in this paper can accurately predict the bearing strength of reinforced concrete under strong earthquakes, and then accurately analyze the concrete damage constitutive model under stress conditions, so as to improve the seismic strength of buildings. Under earthquake action, the yield elements of frame columns are mainly concentrated in the first floor, while the yield elements of frame beams and yield braces are widely distributed. The additional axial force after BRB post strengthening increases the axial force of the braced frame columns, which makes the plastic hinge at the column end develop in the later stage. Except for the column end, the fiber strain of the flange and web of the non-column end section is greater than that of SED supported steel frames. Under some working conditions, the full section of the braced frame columns yields, and the middle section has instability risk and severe plasticity. The SED braced steel frame has uniform deformation of all structures in the first floor under the earthquake action, and the frame column has no buckling under compression. The plastic hinge expansion at the column end is low. As the inter story displacement angle is slightly greater than that of the BRB steel frame, the fiber strain at the column end of the first floor is greater than the column half height and the column mid-section. The proportion of cumulative hysteretic energy dissipation of SED braced steel frames and BRB steel frames along the height distribution is similar, but the proportion of energy dissipation of each layer of the SED braced steel frames is higher, the distribution of energy dissipation is more in line with the requirements of the “energy seismic design method”, and the secondary structures first yield and consume more energy under the earthquake action. SED bracings achieve the medium-term expectation of the “energy seismic design method” to guide more seismic energy into the secondary structures, the purpose of protecting the main structure.
5. Conclusions
Based on the engineering background of 8-degree high-rise steel frame-brace, the seismic performance and design methods of ordinary braced steel frame, buckling restrained braced (BRB) steel frame and sacrificial energy-dissipation steel frame are studied through numerical simulation and theoretical analysis. Based on the actual project, a 15 story steel frame-supporting structure is designed, and the Python modeling script written by myself is used to model in OpenSees. Through the script, the simulation results are analyzed, and the differences of mechanical properties and seismic response results of different steel supports in the frame structure are analyzed and compared. The ordinary steel support will buckle under the axial compression, and the support itself is prone to local instability and steel tearing, resulting in its poor energy dissipation capacity, insufficient ductility, and poor resilience after the earthquake. At the same time, repeated buckling will aggravate the earthquake damage and reduce the safety of the structure. Due to the constraint of the sleeve, buckling restrained brace (BRB), is not conducive to the security of components. The research on the seismic strength and seismic performance of high-rise buildings with reinforced concrete as the main body has always been the focus of building structure and building theory research. Under the strong earthquake load, the sway response of the push-pull lateral eccentric structure of the reinforced concrete frame beam-column structure appears, and the seismic model of the sway response of the reinforced concrete eccentric structure under the strong earthquake load is studied to improve the seismic strength of the reinforced concrete. In this paper, firstly, the mechanical analysis model for the structure of steel frame-precast steel reinforced concrete (SRC) infill wall with lateral force resisting is constructed, and the structural mechanical analysis test design of reinforced concrete eccentric structure under strong earthquake load is carried out to improve the seismic model under shaking response. The test analysis shows that the reinforced concrete seismic model designed in this paper can accurately predict the bearing strength of reinforced concrete under strong earthquake, then accurately analyze the concrete damage constitutive model under the stress conditions, and improve the seismic capacity of the building.
References
-
X. Chen and H. Wang, “Impact of warming temperature on asphalt pavement overlay performance and cost: case study in New Jersey,” Road Materials and Pavement Design, Vol. 23, No. 12, pp. 2886–2899, Dec. 2022, https://doi.org/10.1080/14680629.2021.1991840
-
H. Mujtaba, U. Khalid, Z. Ur Rehman, and K. Farooq, “Recycling of reclaimed subbase materials in flexible pavement design,” Road Materials and Pavement Design, Vol. 23, No. 12, pp. 2713–2732, Dec. 2022, https://doi.org/10.1080/14680629.2021.1995470
-
Q. F. Adam, E. Levenberg, T. Ingeman-Nielsen, and A. Skar, “Modeling the use of an electrical heating system to actively protect asphalt pavements against low-temperature cracking,” Cold Regions Science and Technology, Vol. 205, p. 103681, Jan. 2023, https://doi.org/10.1016/j.coldregions.2022.103681
-
Chen Chuang, Yu Peng, and Wang Yinhui, “A two-step method for structural damage identification based on Mahalanobis distance accumulation and EMD,” Journal of Vibration and Shock, Vol. 38, No. 13, pp. 142–150, 2019.
-
H. Shi, K. Worden, and E. J. Cross, “A cointegration approach for heteroscedastic data based on a time series decomposition: An application to structural health monitoring,” Mechanical Systems and Signal Processing, Vol. 120, pp. 16–31, Apr. 2019, https://doi.org/10.1016/j.ymssp.2018.09.036
-
Yang Zhichun, Zhang Muyu, and Wang Le, “Damage detection of fastener loosening of aircraft stiffened panel by auto correlation analysis,” Zhendong yu Chongji, Vol. 30, No. 11, pp. 13–16, 2011.
-
Wang Hui, Wang Le, and Tian Run-Ze, “Structural damage detection using correlation functions of time domain vibration responses and data fusion. engineering mechanics,” Engineering Mechanics, Vol. 37, No. 9, pp. 30–37, 111, Sep. 2020, https://doi.org/10.6052/j.issn.1000-4750.2019.10.0588
-
G. F. Gomes, Y. A. D. Mendéz, P. Da Silva Lopes Alexandrino, S. S. Da Cunha, and A. C. Ancelotti, “The use of intelligent computational tools for damage detection and identification with an emphasis on composites – A review,” Composite Structures, Vol. 196, pp. 44–54, Jul. 2018, https://doi.org/10.1016/j.compstruct.2018.05.002
-
M. Jancosek and T. Pajdla, “Exploiting visibility information in surface reconstruction to preserve weakly supported surfaces,” International Scholarly Research Notices, Vol. 2014, pp. 1–20, Aug. 2014, https://doi.org/10.1155/2014/798595
-
Y.F. Liu, X. Nie, J.S. Fan, and X.G. Liu, “Image‐based crack assessment of bridge piers using unmanned aerial vehicles and three‐dimensional scene reconstruction,” Computer-Aided Civil and Infrastructure Engineering, Vol. 35, No. 5, pp. 511–529, May 2020, https://doi.org/10.1111/mice.12501
-
Wang Yuanqing et al., “Experimental study on deformation performance of I-section beam with longitudinally variable thickness flanges,” Journal of Harbin Institute of Technology, Vol. 49, No. 12, pp. 24–31, 2017, https://doi.org/10.11918/j.issn.0367-6234.201612103
-
Wang Jue and Zhou Ding, “A modeling method for soil-foundation wind turbine seismic analysis based on foundation impedance,” Applied Mathematics and Mechanics, Vol. 39, No. 11, pp. 1246–1257, 2018, https://doi.org/10.21656/1000-0887.390114
-
Meng Bao, Zhong Wei-Hui, and Hao Ji-Ping, “Experimental study on anti-collapse performance for beam-column assemblies with bolt and weld rigid connection based on different span ratio,” Engineering Mechanics, Vol. 35, No. 1, pp. 79–87, Jan. 2018, https://doi.org/10.6052/j.issn.1000-4750.2016.09.0672
-
H. Duan, S. Chen, and J. Song, “Characterizing regional building energy consumption under joint climatic and socioeconomic impacts,” Energy, Vol. 245, p. 123290, Apr. 2022, https://doi.org/10.1016/j.energy.2022.123290
-
Q. Fu, K. Li, J. Chen, J. Wang, Y. Lu, and Y. Wang, “Building energy consumption prediction using a deep-forest-based DQN method,” Buildings, Vol. 12, No. 2, p. 131, Jan. 2022, https://doi.org/10.3390/buildings12020131
-
Q. Zhou and R. Ooka, “Implementation of a coupled simulation framework with neural network and Modelica for fast building energy simulation considering non-uniform indoor environment,” Building and Environment, Vol. 211, p. 108740, Mar. 2022, https://doi.org/10.1016/j.buildenv.2021.108740
-
M. Singh and R. Sharston, “Quantifying the dualistic nature of urban heat Island effect (UHI) on building energy consumption,” Energy and Buildings, Vol. 255, p. 111649, Jan. 2022, https://doi.org/10.1016/j.enbuild.2021.111649
-
S. Wenninger, C. Kaymakci, and C. Wiethe, “Explainable long-term building energy consumption prediction using QLattice,” Applied Energy, Vol. 308, p. 118300, Feb. 2022, https://doi.org/10.1016/j.apenergy.2021.118300
-
R. Alsharif, M. Arashpour, E. M. Golafshani, M. R. Hosseini, V. Chang, and J. Zhou, “Machine learning-based analysis of occupant-centric aspects: Critical elements in the energy consumption of residential buildings,” Journal of Building Engineering, Vol. 46, p. 103846, Apr. 2022, https://doi.org/10.1016/j.jobe.2021.103846
-
J. Wei and Longqian Chen, “3D virtual technology for space design in green building energy-saving design,” International Journal of Global Energy Issues, Vol. 43, No. 1, pp. 91–98, 2021.
-
Q. Lin, “Research on green building energy saving and environmental protection design based on BIM Technology,” in IOP Conference Series: Earth and Environmental Science, Vol. 514, No. 3, p. 032010, May 2020, https://doi.org/10.1088/1755-1315/514/3/032010
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Xiaohui Wang: writing-original draft preparation. Hui Zhang: conceptualization and methodology. Xiaolong Hu: data curation and formal analysis.
The authors declare that they have no conflict of interest.
