Analysis of the ammunition explosion seismic wave propagation law

1. Introduction

Many damage parameters will be produced in the ammunition explosion process, and seismic wave is one of the main damage parameters [1]. Clarifying the explosive seismic wave propagation attenuation law is of great significance to accurately evaluate the ammunition damage power and guide the ammunition structure design [2-5]. Therefore, in this study, the measured test research is carried out for the ammunition explosive seismic wave, and the propagation attenuation law of explosive seismic wave is analyzed.

At present, researchers at home and abroad have conducted relevant research on the explosive seismic wave propagation and attenuation law, and have made certain research results. For example, Ma K. [6] et al. studied the building structure influence on the peak velocity and vibration frequency of seismic wave propagation by establishing a reinforced concrete plant model, conducting explosion tests outside and inside the model and measuring the corresponding seismic wave signal, fitting its peak velocity and using the wavelet packet transform analysis method. Chen Y. H. [7] et al. tested the seismic wave induced by ground explosion, and analyzed its time-space evolution and frequency characteristics according to the test results, and obtained the difference between natural seismic wave and induced seismic wave. Wang L. Q. [8] et al. designed a corresponding seismic wave measurement scheme and set up a seismic wave measurement system in order to test the vibration intensity of the seismic wave generated by the cloud explosion, and used the particle vibration velocity theoretical formula to fit and analyze the measured seismic wave. The fitting function relationship has good consistency with the actual test data in reflecting the explosion seismic wave vibration velocity distribution law. Yang L. [9] et al. obtained the explosive seismic wave characteristics in terms of band dominant frequency, duration, near-field initial motion, etc., the explosive seismic wave propagation rules in rock and soil, and the differences between these characteristics and natural seismic wave by analyzing the site effect of explosive vibration speed and explosive vibration frequency, and the relationship between explosive vibration speed and explosive equivalent and seismic wave propagation distance. Liu H. Q. [10] and others, in order to study the wave process in rock and soil mass under the shallow buried underground explosion action, effectively combined the basic theoretical knowledge of explosion mechanics, elasticity and higher mathematics, established a calculation model for the movement of seismic wave on the semi infinite medium free surface under the shallow buried explosion action, and calculated the explosion seismic wave horizontal and vertical displacement with Matlab programming. Yang J. H. [11, 12] et al. studied the influence of ground stress on rock mass blasting cracking and the radiation mode and energy characteristics of blasting seismic wave by using the SPH-FEM coupling numerical simulation method. The results show that the rock blasting crack zone shape change under the ground stress action has a significant impact on the blasting seismic wave energy and composition. In the same year, they studied the influence of the ground stress field on rock blasting cracking and the seismic wave energy outside the cracking area. The results show that with the ground stress level increase, the scope of the rock blasting crushing zone shrinks and the crack propagation speed decreases. The cracks in the crushing zone mainly extend along the direction of the maximum principal stress in the non-hydrostatic geostress field, but the ground stress has little influence on the blasting crushing zone formation. To improve the quality of seismic waves excited by explosive sources in seismic exploration, Mou J. [13] et al. selected air, water, fine sand and rock soil as coupling media, and conducted explosion tests in soil to compare and analyze the coupling media influence on seismic wave characteristics. The test results show that the seismic wave energy generated by the explosive source with water as the coupling medium is relatively high, especially in the range of 25-100 Hz, the energy contrast difference is more obvious. It can be seen from the above research status that at present, some progress has been made in the explosive seismic wave attenuation law at home and abroad, but there is little research on the ground vibration velocity, peak velocity and dimensionless function relationship under the surface explosion condition. However, these research contents are of great significance for accurately understanding the explosive seismic wave propagation law in soil.

In this study, the explosion seismic wave field test under different explosive mass was carried out, the ground vibration velocity time history curve at different measuring points was obtained, and the vibration velocity and acceleration peak value were analyzed. Based on the existing measured data, the explosion seismic wave ground vibration acceleration peak value calculation function is established by using the dimensional analysis method, and the function calculation accuracy is verified by using the measured data.

2. Explosive seismic wave

When the ammunition explodes, it will produce explosive products with high temperature and pressure, which will spread outward from the explosion center at a very high speed and compress the surrounding air, thus forming an explosive shock wave. The explosive shock wave will collide with the ground in the propagation and launch process. In the collision process, part of the energy is converted into seismic wave and propagates in the ground propagation medium [14, 15]. The transformation and source of explosion seismic wave are shown in the Fig. 1.

Explosive seismic wave is a kind of elastic wave [16-18], which can be divided into two types according to the wave basic composition: body wave and surface wave. The body wave includes longitudinal wave and transverse wave. The longitudinal wave (P wave) is a wave with the same propagation direction and particle vibration velocity in the ring. It makes the propagation medium compress or expand, so it is also called tensile wave or densification wave. The longitudinal wave has the lowest energy among the three kinds of waves, and the corresponding peak particle vibration velocity is smaller, but the propagation speed is the fastest. Therefore, the longitudinal wave usually reaches the measuring point first. The shear wave energy is larger than that of the longitudinal wave, and the particle vibration speed is relatively large, but the shear wave propagation speed is smaller than that of the longitudinal wave [19, 20].

Due to the difference between the propagation velocities of shear wave and longitudinal wave in the explosion seismic wave in the above analysis, when testing the explosion seismic wave, at the far-field measuring point, the first arrival is longitudinal wave, followed by shear wave and Rayleigh wave. The shear wave and Rayleigh wave propagation velocities are similar, so the arrival time is relatively similar. Because the Rayleigh wave energy is large, the vibration amplitude is also large. From the vibration velocity time history curve obtained from the explosion seismic wave, the main component is Rayleigh wave.

Fig. 1Explosion seismic wave source

3. Explosion seismic wave test and analysis

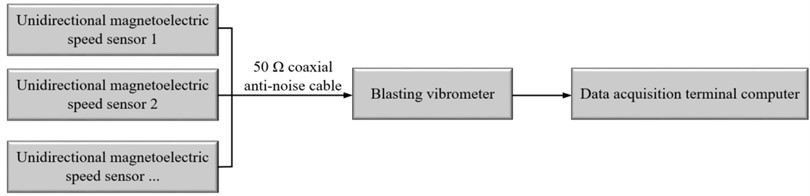
3.1. Seismic wave measurement system

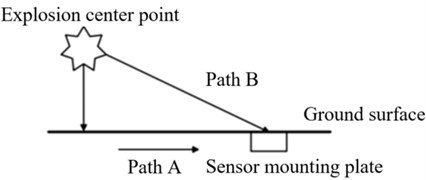
In actual test, TNT explosive mass as 1.25 kg, 5.25 kg, 10.5 kg and 30.75 kg are selected to obtain explosive seismic waves at different measuring points. TNT is suspended 1.5 m from the ground and detonated by detonator. The measuring points are arranged on the same radius along the explosion center. The measuring points distance is 4 m, 5 m, 6.5 m, 8 m, 10 m, 14 m, 16 m, 22 m and 24 m, respectively. There are 9 measuring points in total. In order to equipment and instruments safety in the test process, the blasting vibration meter was dug and placed in the tunnel in the form of iron box packaging, and the blasting vibration meter acquisition mode was set as external contact, the trigger level was 0.1 cm/s, the sampling plastic cloth was 16 kHz, and the sampling time was 5 s. In order to obtain the vibration velocity signal of explosive seismic wave stably and reliably, a large range velocity sensor shall be placed near the explosion center, and the signal cutting top shall be placed during the test. The measuring points layout during the actual test is shown in the Fig. 2.

Fig. 2Seismic wave sensor layout position structural diagram

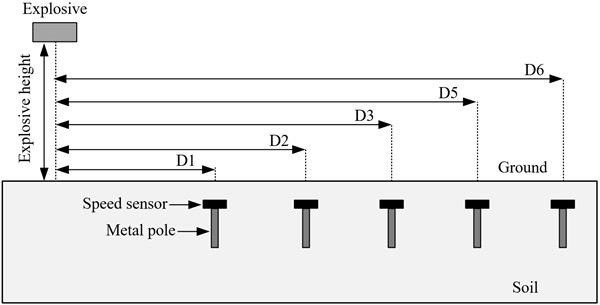
Since the seismic wave at the explosion site is a non-stationary random signal with short duration and rapid mutation, the seismic wave sensor response time should be as short as possible and have a good response rate. Generally, the explosion seismic wave frequency range is 30-300 Hz [21], and the sensor frequency acquisition should meet this range. Due to the harsh environment of the test site and many uncertainties, the test system shall have good reliability to ensure the smooth test.

Fig. 3Explosion seismic wave measurement system

During the actual test, the seismic wave sensor is buried underground, and the sensor is 30 cm away from the ground. The seismic wave sensor and vibrometer are single magnetoelectric speed sensors developed by Chengdu Zhongke measurement and control technology company. The sensor working bandwidth is 5-500 Hz, the sensor output impedance is low, the carrying capacity is strong, and the signal transmission distance is long, its range is 0-2 m/s and 0-35 cm/s respectively. The blasting vibration meter can realize three-channel parallel acquisition, with resolution of 0.01 cm/s, reading accuracy of 0.1 %, A/D digit of 16 bit, and trigger mode including internal trigger and external trigger, and can record up to 1024 segments of data. [22]. It can be concluded that the test system has very good environmental adaptability to the explosion site seismic wave test. The sensors on-site installation method and vibration meters is shown in Fig. 4.

Fig. 4Sensor and vibration meter field installation method

a) Seismic wave sensor site installation mode

b) Vibration meter field installation method

3.2. Analysis on explosion seismic wave propagation law

The above explosion seismic wave measurement system is used to obtain seismic wave signals at different measuring points. There are many explosion seismic wave signals obtained during the actual test, which cannot be displayed one by one. Therefore, we choose the ground vibration velocity time history curve at 4 m, 5 m, 6.5 m, 8 m, 10 m and 12 m with TNT explosive mass of 1.25 kg and 5.25 kg to display. The display results are shown in the following Figs. 5 and 6.

It can be seen from the above explosion seismic waves ground vibration velocity curves at different measuring points that under the same TNT explosive mass, the ground vibration velocity peak value gradually attenuates with the increase of the distance from the measuring point to the explosion center, that is, the vibration velocity peak value is negatively correlated with the distance from the measuring point; With the increase of TNT explosive mass, the ground vibration velocity peak value at the same measuring point gradually increases, that is, the ground vibration velocity peak value is positively correlated with TNT explosive mass.

Fig. 51.25 kg TNT explosion seismic wave ground vibration velocity time history curve

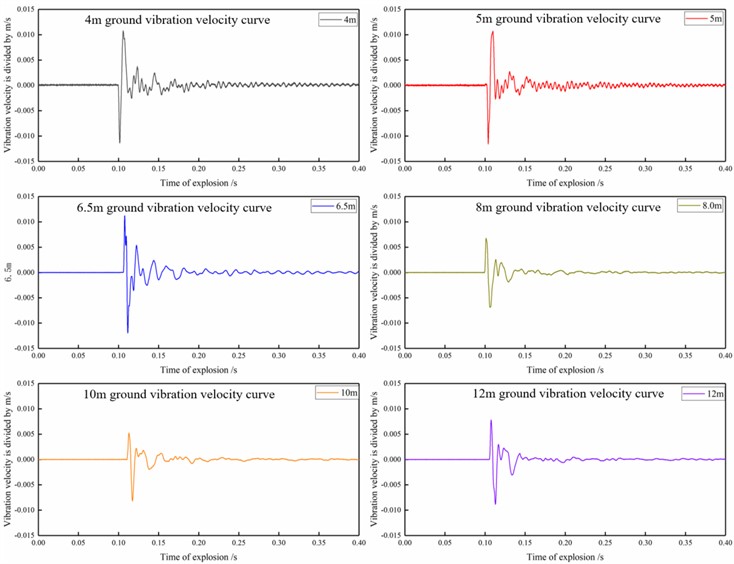
Fig. 65.25 kg TNT explosion seismic wave ground vibration velocity time history curve

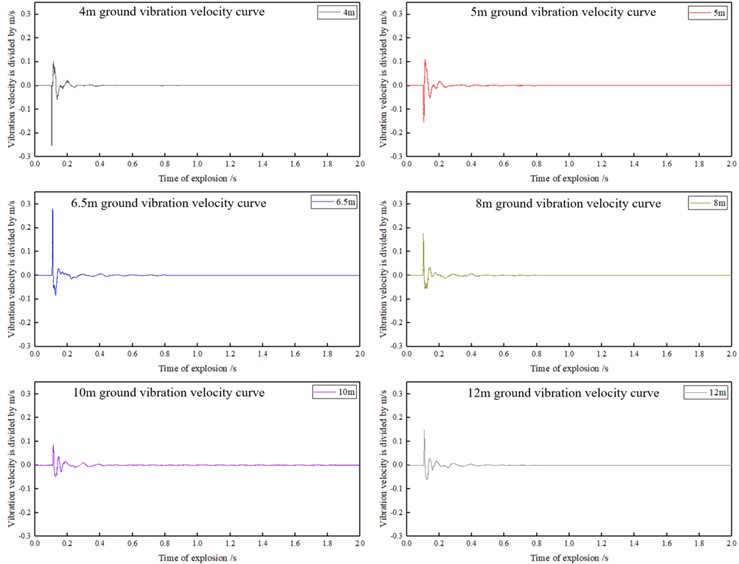
It can be seen from the seismic wave vibration velocity time curve that the explosive seismic wave attenuation rate in the soil is relatively slow, so the explosive seismic wave can travel farther and the vibration lasts longer. Therefore, the explosion seismic wave has the long distance and lasting damage characteristics.

In the process of actual explosion seismic wave damage evaluation, the ammunition seismic wave damage power is usually evaluated based on the ground vibration acceleration value. Therefore, after obtaining the ground vibration velocity with time change rule at different measuring points, it is necessary to conduct differential processing on the obtained vibration speed-time signal to obtain the acceleration-time curve corresponding to the speed-time curve, the ground vibration acceleration peak value is extracted. When extracting the ground vibration peak acceleration, it is necessary to combine the peak vibration velocity arrival time to accurately extract the peak acceleration value from the vibration acceleration-time curve. After processing the above obtained vibration speed-time signal, the explosion seismic wave ground vibration acceleration peak value at different measuring points with different TNT explosive mass is shown in the Table 1.

Table 1Ground vibration acceleration peak values at different measuring points for different TNT explosive mass

5.25 kg		10.5 kg		30.75 kg
Distance (m)	Peak (m/s2)	Distance (m)	Peak (m/s2)	Distance (m)	Peak (m/s2)
4	195.706	4	287.738	4	576.0620
5	73.1282	5	–	5	322.4336
6.5	62.7998	6.5	131.765	6.5	259.0813
8	–	8	107.168	8	–
10	57.9752	10	79.7945	10	151.3038
12	34.5111	12	49.8975	12	–
14	–	14	45.8975	14	107.7707
16	26.931	16	–	16	–
18	18.1968	18	–	18	63.1824
20	–	20	26.2364	20	41.0642
22	11.5826	22	17.9569	22	31.8797
24	9.8979	24	14.5445	24	22.4829
Note: – is to obtain valid data during the test

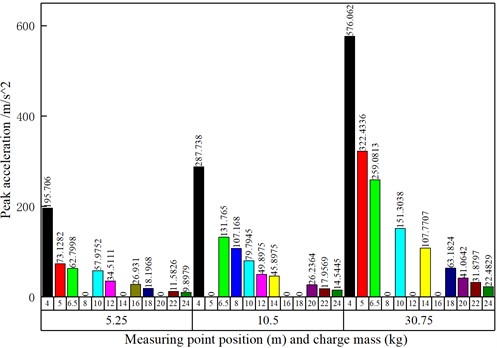
From the above ground vibration acceleration peak table, the explosion seismic wave propagation law can be quantitatively analyzed, to more clearly obtain the change law of ground vibration acceleration with TNT charge quality and measuring point position. We draw the multi-factor index histogram as shown in Fig. 7 with TNT explosive mass and measuring point distance as independent variables and ground vibration acceleration peak as dependent variables.

According to the analysis of the data table and histogram of the explosion seismic wave ground particle vibration acceleration peak, under the same TNT explosive mass, the ground vibration acceleration peak gradually decreases with the increase of the distance between the measuring points, and the vibration acceleration peak attenuation rate is not consistent, but changes with the change of the distance between the measuring points and the explosion center. It is mainly reflected in that the faster the acceleration peak attenuation rate is at the position close to the blast core, the slower the acceleration peak attenuation rate is at the position far away from the blast core, and the negative correlation between the peak attenuation rate of ground vibration acceleration and the distance from the blast core of the measuring point. With the increase of TNT explosive mass, the ground vibration acceleration peak value at the same measuring point also increases, and the two are positively correlated. But the increase rate is not linear. In addition, the ground vibration acceleration change law is also closely related to the explosives essential properties. From the explosive seismic wave ground particle vibration acceleration peak value, it can be concluded that the ground vibration acceleration peak value caused by the ammunition explosion is very large in the near field, which can completely produce a large damage effect on the target. Therefore, when evaluating the ammunition explosive damage power, explosive seismic wave is one of the damage evaluation parameters that cannot be ignored. It is very necessary to study the propagation and distribution law of explosive seismic wave.

Fig. 7Acceleration peak values at different measuring points for different TNT explosive mass (Note: in the above particle vibration acceleration peak histogram, 0 represents that no effective vibration acceleration data is obtained in the actual test process)

4. Particle vibration acceleration functional relationship model

As only the vibration acceleration signals on a limited number of measuring points can be obtained in the actual testing process, it is impossible to analyze the vibration acceleration peak values at different measuring point distances during the ammunition explosion. Therefore, in order to solve this problem, the factors that affect the explosive seismic waves ground vibration acceleration are analyzed by dimensional analysis method, Obtain the functional correspondence between the independent variable and the dependent variable [23].

The analysis shows that the factors affecting the explosion vibration acceleration are: 1. Explosive parameters: TNT explosive mass $Q$, chemical energy released by unit mass TNT explosive $E_0$, explosive products expansion index ${\gamma }_e$; 2. Air parameters: initial pressure $p_0$, initial density ${\rho }_0$; 3. Soil parameters: soil density ${\rho }_s$, soil elastic modulus $E$, sound velocity $c$; Geometric parameters: distance between explosion center $R$, height $H$ from explosion center to seismic measuring point [24, 25].

The explosion vibration acceleration can be expressed as:

Considering that the explosives used in simulation calculation and test are of the same type and different equivalents, and the explosion occurs under standard atmospheric pressure, namely:

Then the explosion vibration acceleration expression can be simplified as:

Therefore, the charge amount $Q$, explosion center distance $R$ and sound velocity $c$ are selected as the reference physical quantities, and the each physical quantity dimension power coefficients are shown in Table 3.

Table 4 can be obtained by elementary matrix transformation similar to Table 3.

According to $\mathrm{\Pi }$ theorem, dimensionless expression can be given:

For the research object, $c$, ${\rho }_s$, $E$ can be considered as a constant, then $v$ has a functional relationship with $R^2/Q$ and $H/R^2$, which can be expressed as:

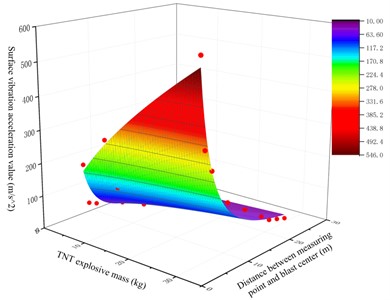
Use the above obtained ground particle vibration acceleration signal to carry out nonlinear adaptive fitting of the above function relationship, and the data and function relationship curve fitting results are shown in the Fig. 8.

Through nonlinear fitting, we can get the above function relationship in which $a_0=$494.16531, $b_0=$ –0.63852, $b_1=\text{0.13494}$ and the error squares sum is 0.97448. Therefore, the above function relationship can be expressed as:

It can be seen from the ground vibration acceleration peak value calculation function formula of the explosion site established above that the impact vibration acceleration generated on the ground during the ammunition explosion process is positively correlated with the TNT explosive mass, and negatively correlated with the distance between the measuring point and the explosion center. Therefore, in the actual operation process, the damage effect caused by the explosion seismic wave is mainly concentrated at the location near the blast core, and the seismic wave damage effect is weak at the location far away from the blast core.

Fig. 8Function relation nonlinear fitting result

To verify the above function relationship expression calculation accuracy, the fitting accuracy of the function relationship is verified by using the ground particle vibration acceleration data obtained during the 5.25 kg, 10.5 kg and 30.75 kg TNT explosion. The coincidence between the test data and the function relationship is shown in Fig. 9.

Fig. 9Test data and function relationship fitting results comparison chart

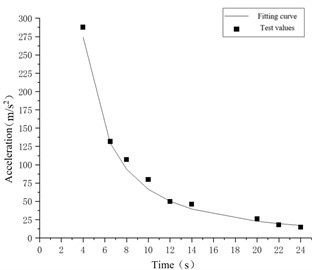
a) 5.25 kg TNT test data and function calculation results comparison chart

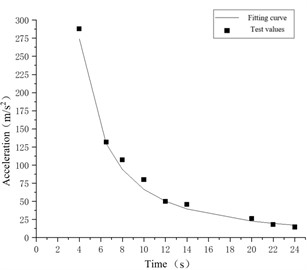
b) 10.5 kg TNT test data and function calculation results comparison chart

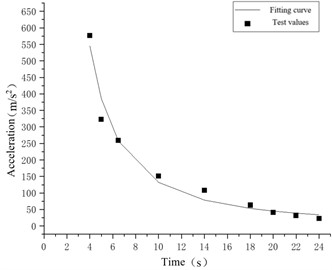
c) 30.75 kg TNT test data and function calculation results comparison chart

From the above fitting results, it can be seen that the ground particle vibration acceleration function formula has a very good fitting trend for the explosion seismic wave acceleration, and most of the data obtained in the actual test process can be consistent with the model calculation results. It can be seen from the above figure that part of the test data does not completely coincide with the curve, mainly because the test site surface propagation medium is uneven during the actual test process, and the elevation difference between different measuring points and the location of the explosion center is also different, which results in the influence of the seismic wave propagation and attenuation law, making some of the test data change, but these data can be evenly distributed on both sides of the fitting curve, Therefore, the calculation function relationship of ground vibration acceleration peak value established in this study can still reflect the propagation and distribution law of ammunition explosive seismic wave, and can provide scientific and effective data support for the explosive seismic wave damage power evaluation.

5. Conclusions

This study has carried out relevant research on the ground vibration velocity and acceleration generated in the ammunition explosion process. Aiming at the explosion seismic wave propagation characteristics, a ground vibration velocity measurement system has been established, and the obtained particle vibration velocity signal and vibration acceleration signal have been analyzed. It is clear that the ground vibration velocity peak value is positively correlated with the TNT explosive quality, and negatively correlated with the distance from the measuring point to the detonation center, In addition, the explosion seismic wave ground vibration velocity attenuation rate is fast in the near field and slow in the far field; The functional relationship between the seismic wave particle vibration acceleration in the explosion field and the TNT explosive mass and the distance between the measuring points established based on the dimensional analysis method has a good interpretation ability for the measured data, it can be used in engineering to provide scientific and effective data support for the ammunition explosive damage evaluation.