Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials

Abdrakhmanov, Yerkesh; Kalimbetov, Galym

doi:10.21595/vp.2023.23187

Vibroengineering Procedia

Browse Procedia

Published: 18 May 2023

Check for updates

Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials

Yerkesh Abdrakhmanov¹

Galym Kalimbetov²

^{1, 2}Department of Energy, JSC Academy of Logistics and Transport, Almaty, Kazakhstan

Corresponding Author:

Yerkesh Abdrakhmanov

Cite the article Download PDF

Downloads 104

CrossRef Citations 1

Abstract

Electric arc melting of oxide materials under the influence of an external electromagnetic field is a high-current and high-temperature technological process, accompanied by powerful electric and magnetic fields and complex structural motion of the melt. In the general case, the movement of the melt in the bath of an electric arc installation is determined by a combination of thermocapillary, thermal concentration, thermal and electromagnetic convections. In this work, based on the analysis of convective flows and the calculation of the integral vortex field of Archimedes forces and electromagnetic forces in the bath, using the OKB-2126A ore-thermal furnace for melting oxide refractory materials as an example, an assessment of thermal and electromagnetic convections was carried out. For the first time it has been established that the value of the integral vorticity of the field of electromagnetic forces in the depth of the bath exceeds the integral vorticity of the field of Archimedes forces by 3-4 times. In real objects, this difference is even greater, since, compared to those accepted in the calculations, the actual current density in the bath is higher, and the temperature difference is lower. Thus, electromagnetic convection in ore-thermal furnaces for melting oxide materials significantly exceeds thermal convection and makes a decisive contribution to the formation of the structure and intensity of melt movement.

$Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials$

Highlights

For the first time, it has been established that in ore-thermal furnaces with an electromagnetic device for melting oxide refractory materials.
The integral vorticity of the field of electromagnetic forces in the surface layers is maximum, and gradually decreases with increasing bath depth.
Electromagnetic convection is 3-4 times greater than thermal convection and makes a decisive contribution to the formation of the structure and the intensity of the movement of the melt.

1. Introduction

During electric arc melting of oxide refractory materials, under the influence of an external electromagnetic field, powerful electric and magnetic fields, high temperatures are formed, and under their influence complex structural movements of the melt occur. The resulting convective currents can speed up or slow down the movement of the melt in the bath and thus provide numerous options for non-contact control of heat and mass transfer processes in furnaces. The intensification of the process of melting refractory materials, increasing the productivity of furnaces and reducing the specific power consumption, improving the homogeneity of the melt depend on the ability to control heat-mass transfer and hydrodynamic processes in a liquid bath and create optimal conditions for the flow of technological processes.

In the general case, all processes of electric arc melting of oxide refractory materials in an electromagnetic field are described by the interrelated equations of Maxwell, Navier-Stokes and Fourier heat transfer [1-4]. In general, the movement of the melt in the bath of an electrothermal installation is determined by a combination of electromagnetic, thermo and hydrodynamic processes, consisting of thermocapillary, thermal concentration, thermal and electromagnetic convections [5-7]. According to the estimates of works [6, 7], the intensities of thermocapillary and thermoconcentration convections are insignificant. The main mechanisms of heat transfer in the melt in such installations are electrovortex and thermogravitational convection. However, the issues of interaction between electrovortex and thermogravitational convection for multielectrode furnaces are still insufficiently developed. There are no studies on the interaction of electrovortex, thermogravitational and electromagnetic (under the influence of an external field) convection in ore-thermal furnaces for melting oxide refractory materials. At the same time, MHD processes in electrotechnological units also have a natural origin, which also has a significant impact on its operating modes and the nature of the flow of technological operations, which can be both positive and negative.

Electromagnetic convection in the form of electrovortex flows can arise as a result of the interaction of the electric current in the melt bath with its own magnetic field [8-10], as well as during interaction with an external magnetic field [11, 12]. Electrovortex flows, i.e. electromagnetic convection, formed by the interaction of an electric current with its own magnetic field, becomes noticeable only at very high currents of the order of several tens of kiloamperes [7, 9].

Ore-thermal furnaces for smelting refractory materials operate at currents up to 10-13 kA [13, 14]. In this regard, electrovortex flows under such conditions cannot create sufficiently noticeable convective flows in the furnace bath. Therefore, in ore-thermal furnaces for smelting oxide materials, in order to intensify the smelting process and increase the homogeneity of the physical and chemical composition of the bath, it is necessary to use additional electromagnetic influence from the outside [15, 16].

Thermal (natural) convection is associated with the dependence of the melt density on temperature and occurs when there is a significant temperature inhomogeneity in the bath. For various electrothermal units, their operating modes, melt characteristics, the ratio of electromagnetic and thermal convection is different. Therefore, in order to elucidate their influence on the movement of the melt in the furnace bath, in each specific case, it is necessary to evaluate their ratios.

2. Research methodology

To estimate the intensities of electromagnetic and thermal convection, it is necessary to compare the values of the integral rotors of the Archimedes forces and electromagnetic forces in the characteristic sections of the bath [5, 7].

Temperature inhomogeneity in the furnace bath leads to a change in the density of the melt and the appearance of Archimedes forces:

1

\vec{f_{a}} = ρ g = - ρ_{o}^{} g (1 - β Δ T) {\vec{e}}_{z},

where $ρ$ – is the average density over the volume of the bath; $β$ – is the thermal expansion coefficient; $Δ Τ$ – is the temperature deviation from the average; $ρ = ρ_{o} (Ι - β Δ Τ)$ – the Boussinesq approximation.

The condition for the appearance of thermal convection has the form:

2

\vec{f_{a}} = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{0}{\partial x} & \frac{0}{\partial y} & \frac{0}{\partial z} \\ 0 & 0 & f_{a} \end{matrix}| = {\vec{e}}_{x} \frac{\partial t a}{\partial y} - {\vec{e}}_{y} - \frac{\partial t a}{\partial x} = {\vec{e}}_{x} β ρ q \frac{\partial T}{\partial y} - {\vec{e}}_{y} β p_{0} q \frac{\partial T}{\partial x} \neq 0,

that is, for its occurrence, there must be a temperature gradient in the horizontal direction:

3

{(∆ T)}_{0} = T_{e} - T_{w} .

The available literature data and our own experimental measurements of temperatures in the bath of an ore-thermal furnace during the melting of oxide refractory materials show that the temperature gradient decreases with depth. Moreover, it can be assumed that the change in the temperature gradient with depth occurs according to a linear law:

4

∆ T = (T_{e} - T_{w}) (1 - \frac{z}{H}),

where $T_{e}$ – is the temperature of the core of the melt; $T_{w}$ – is the temperature of the furnace wall; $h$ – is the depth of the bath.

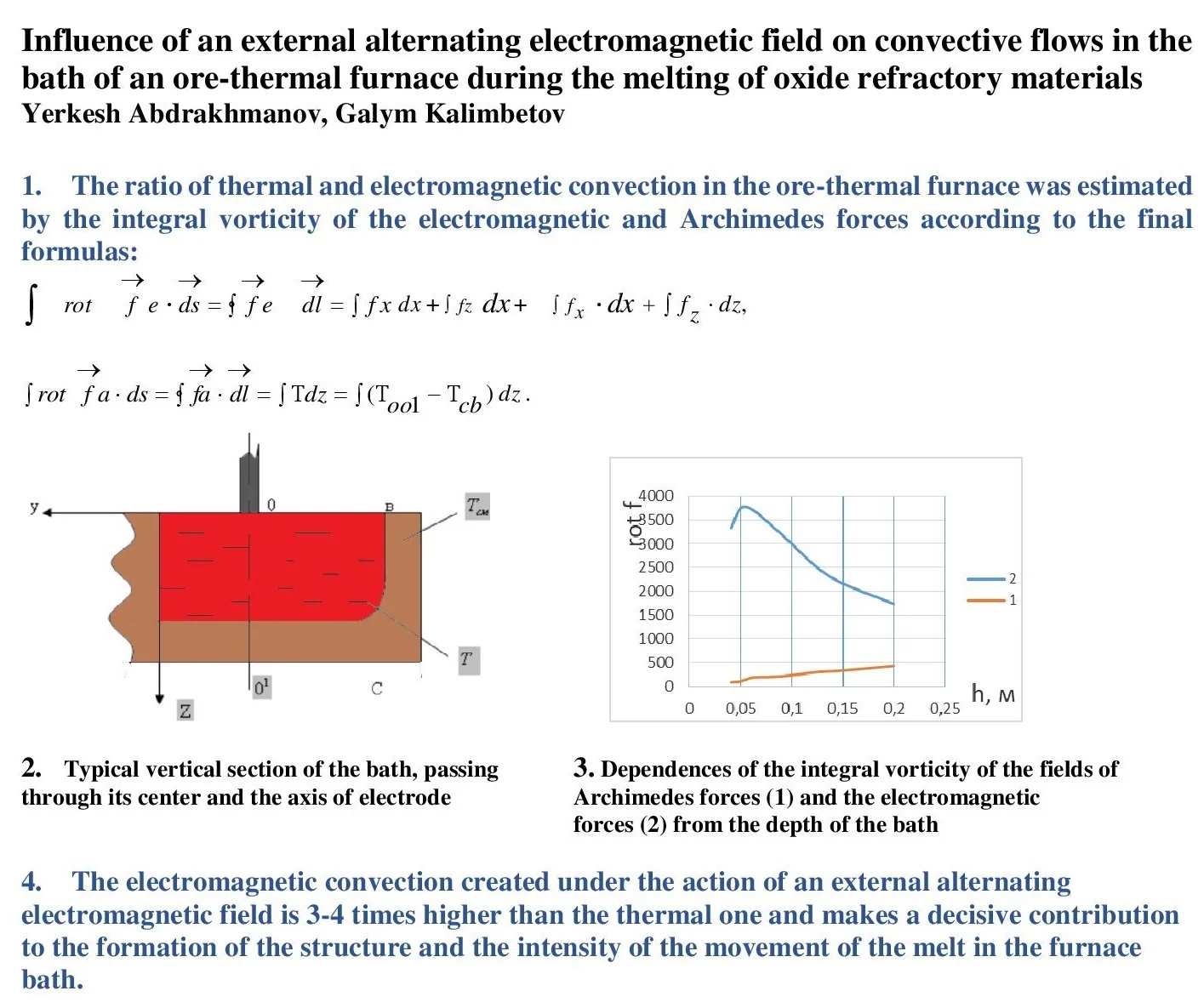
The largest temperature gradient in the bath of an electric arc furnace occurs between the subelectrode, where the melt is overheated due to the increased current density and the presence of an arc, and the peripheral zones. Thus, it is necessary to calculate the integral vorticities in the vertical section of the pool passing through its center and the electrode axis (Fig. 1).

Fig. 1Typical vertical section of the bath, passing through its center and the axis of the electrode

The electromagnetic force density is expressed by the formula:

5

\vec{f_{e}} = \vec{j} * \vec{B},

where $j$ – is the current density; $B$ – magnetic induction of the external field.

The current density in the bath of a 3-phase ore-thermal furnace by the superposition method [18] is determined as the sum of all currents from the expression:

6

\vec{j} = \sum_{i = 1}^{3} \vec{j} = \sum_{i = 1}^{3} \vec{j} * c o s [ω t (i - 1) \frac{2 π}{3}] .

Magnetic induction of the external field:

7

B_{x} = - \frac{π μ_{0} A_{0}}{\sqrt{δ_{1}^{2} + δ_{2}^{2}}} * e^{- δ_{1} (z_{1} - z) / τ} * \cos (ω t - α x + φ_{0} - δ_{2} \frac{z_{1} - z}{τ} + a r c t g \frac{δ_{1}}{δ_{2}}),

8

B_{z} = μ_{0} A_{0} e^{- δ_{1} (z_{1} - z) / τ} * \cos (ω t - α x + φ_{0} - δ_{2} \frac{z_{1} - z}{τ}),

where $α = π / τ$ ; $β = \sqrt{α^{2} + i 5 μ_{0} ω S}$ ; $β τ = \sqrt{π^{2} + i ω_{τ}} = δ_{1} + δ_{2}$ ; $\bar{ω_{τ}} = σ μ_{0} ω τ^{2}$ .

Substituting the values of $j$ and $B$ into Eq. (5) we get:

9

{\vec{f}}_{e} = \sum_{i = 1}^{3} {\vec{j}}_{o c i} * c o s [ω t - 2 π (i - 1) / 3] * \vec{B_{B x}} * {\vec{i}}_{x} * \cos (ω t - α x + φ_{0} - δ_{2} \frac{z_{1} - z}{τ} + a r c t g \frac{δ_{1}}{δ_{2}}) + \sum_{i = 1}^{3} {\vec{j}}_{o c i} * c o s [ω t - \frac{2 π (i - 1)}{3}] * B_{B z} * {\vec{i}}_{z} \cos (ω t - α x + φ_{0} - δ_{2} \frac{z_{1} - z}{τ}) * e^{- δ_{1} (z_{1} - z) / τ} .

Averaging over time over the period of the electromagnetic force, we end up with:

10

〈\vec{f}〉 = \frac{1}{2} \sum_{i = 1}^{3} {\vec{j}}_{x} \{B_{B x} * {\vec{i}}_{x} * c o s [α x - φ_{0} \frac{2 π (i - 1)}{3} + δ_{2} \frac{z_{1} - z}{τ} - a r c t g \frac{δ_{1}}{δ_{2}} + B_{B z} * {\vec{i}}_{z} * c o s [α x - φ_{0} \frac{2 π (i - 1)}{3} + δ_{2} \frac{z_{1} - z}{τ}]\} e^{- δ_{1} (z_{1} - z) / τ}

The resulting expression allows you to calculate the electromagnetic force field in the bath of a 3-phase ore-thermal furnace with an electromagnetic device.

The calculation of the electromagnetic force is greatly simplified if the formulas are presented in relative units.

The current density of each electrode can be represented as components:

11

{\vec{j}}_{i} = {\vec{j}}_{i x} * {\vec{j}}_{x} + {\vec{j}}_{i y} * {\vec{j}}_{y} + {\vec{j}}_{i z} * {\vec{j}}_{z} .

The electromagnetic force is calculated by the formula:

12

\vec{f_{e}} = {\vec{j}}_{} * \vec{B} = |\begin{matrix} {\vec{i}}_{x} & {\vec{i}}_{y} & {\vec{i}}_{z} \\ {\vec{j}}_{x} & {\vec{j}}_{y} & {\vec{j}}_{z} \\ B_{x} & B_{y} & B_{z} \end{matrix}| = {\vec{i}}_{x} * {\vec{j}}_{y} * B_{z} + {\vec{i}}_{y} ({\vec{j}}_{z} B_{x} - {\vec{j}}_{x} B_{z}) + {\vec{i}}_{z} * {\vec{j}}_{y} * B_{x} .

Rotor electromagnetic forces:

13

r o t \vec{f} = |\begin{matrix} {\vec{i}}_{x} & {\vec{i}}_{y} & {\vec{i}}_{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial} \\ f_{x} & f_{y} & f_{z} \end{matrix}| = {\vec{i}}_{x} (\frac{\partial f z}{\partial y} - \frac{\partial f y}{\partial z}) + {\vec{i}}_{y} (\frac{\partial f z}{\partial x} - \frac{\partial f x}{\partial z}) + {\vec{i}}_{z} (\frac{\partial f y}{\partial x} - \frac{\partial x}{\partial y}) .

The values of the integral vorticity of the fields electromagnetic forces and of Archimedes forces are calculated by the formulas:

14

\int r o t {\vec{f}}_{e} d s = \oint {\vec{f}}_{e} d l = \int f_{x} d x + \int f_{z} d x + \int f_{x} d x + \int f_{z} d z,

15

\int r o t {\vec{f}}_{a} d s = \oint {\vec{f}}_{a} d l = \int T d z = \int (T_{o o 1} - T_{c b}) d z,

Calculations in relative units were carried out for the OKB-2126A ore-thermal furnace used for melting refractory materials with an electromagnetic stirrer installed under the furnace bath. The technical characteristics of the OKB-2126A furnace are presented in Table 1.

Table 1Technical characteristics of the OKB-2126A ore-thermal furnace

No	Parameter	Meaning
1	Bath diameter	1,8
2	Bath depth, m	0,4
3	Electrode decay diameter, m	0,8
4	Electrode diameter, m	0,25
5	Rated line voltage, V	123-244
6	Rated current, A	4300
7	Apparent power, kVA	1800

The calculation of the field of electromagnetic forces and its rotor, integral rotors of the field of electromagnetic forces and Archimedes forces was carried out using numerical methods [19, 20] on the basis of a calculation program specially developed for this purpose.

3. Research results

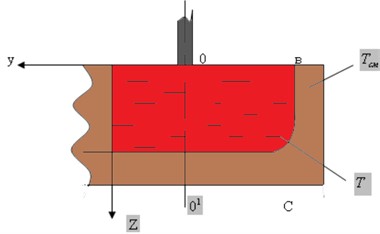
The results of calculations from the integral vorticity of the fields of Archimedes forces and electromagnetic forces for the depth of the bath of the OKB-2126A ore-thermal furnace and $I =$ 3 kA are shown in Fig. 2.

As can be seen from the graphs (Fig. 2), the integral vorticity of the field of Archimedes forces increases with increasing depth of the bath within 0.00-0.20 m from 0 to 470. The integral vorticity of the field of electromagnetic forces in the surface layers has a maximum value of 3980, then with an increase the depth of the bath to 0.20 m is gradually reduced until 1700. Despite this, the value of the integral vorticity of the field of electromagnetic forces, even in the depth of the bath, exceeds the integral vorticity of the field of Archimedes forces by 3-4 times. In real objects, this difference is even greater, since the current density in the bath is higher compared to those accepted in our calculations, and the temperature difference over its volume is lower.

The results obtained are confirmed by the data of experimental melts of a number of oxide refractory materials (forsterite, forsterite-chromite, corundum) with electromagnetic stirring. On the entire surface of the bath of an ore-thermal furnace, when using electromagnetic influence, an intense directed movement of the melt is observed. While in the absence of an external electromagnetic field, movements occur only in the sub-electrode zones. The significance of electromagnetic convection in the presence of an external electromagnetic field is also confirmed by the fact that the blocks obtained in this way have a uniform dense structure.

Fig. 2Dependences of the integral vorticity of the fields of Archimedes forces (1) and electromagnetic forces (2) from the depth of the bath

4. Conclusions

As a result of the research, it was found that the integral vorticity of the field of Archimedes forces increases with an increase in the depth of the bath, and the integral vorticity of the field of electromagnetic forces in the surface layers is maximum, then gradually decreases with increasing depth of the bath. Despite this, the value of the integral vorticity of the field of electromagnetic forces, even in the depth of the bath, exceeds the integral vorticity of the field of Archimedes forces by 3-4 times.

Thus, as a result of the studies carried out, for the first time it was established that in ore-thermal furnaces for melting oxide refractory materials, electromagnetic convection created under the influence of an external alternating electromagnetic field is 3-4 times higher than the thermal one and makes a decisive contribution to the formation of the structure and the intensity of the movement of the melt.

References

R. J. Hosking and R. L. Dewar, Fundamental Fluid Mechanics and Magnetohydrodynamics. Singapore: Springer Singapore, 2016, https://doi.org/10.1007/978-981-287-600-3

Publisher
V. I. Dubodelov, “On the application of magnetohydrodynamics in foundry technologies. History, state, prospects,” (in Russian), Journal of Metallurgy engineering, No. 3, pp. 28–34, 2019.

Search CrossRef
I. M. Kirko and G. E. Kirko, “Magnetic hydrodynamics. Modern vision of problems,” (in Russian), Regular and Chaotic Dynamics, Institute of Computer Research, 2019.

Search CrossRef
A. G. Kulikovsky and G. A. Lyubimov, Magnetic Hydrodynamics. (in Russian), Logos, 2011, p. 328.

Search CrossRef
T. Zürner, F. Schindler, T. Vogt, S. Eckert, and J. Schumacher, “Combined measurement of velocity and temperature in liquid metal convection,” Journal of Fluid Mechanics, Vol. 876, pp. 1108–1128, Oct. 2019, https://doi.org/10.1017/jfm.2019.556

Publisher
O. Kazak and O. Semko., “Modelling of electrovortex and heat flows in dc arc furnaces with bottom electrode,” (in Russian), Journal of Processes, Products and Applications, Vol. 40, pp. 619–624, 2013.

Publisher
A. L. Kukharev, “Melt flows in a multielectrode arc furnace under conditions of electrovortex and natural convection,” (in Russian), Journal of Vestnik LNU, Vol. 7, No. 25, pp. 217–223, 2019.

Search CrossRef
H. Molder, J. Jarvik, T. Vaimann, and R. Gordon, “Multi-electrode arc furnace technology with improved metal processing capability using current driven mixing,” in 2012 11th International Conference on Environment and Electrical Engineering (EEEIC), pp. 313–316, May 2012, https://doi.org/10.1109/eeeic.2012.6221394

Publisher
I. M. Yachikov and N. P. Larina, “Evaluation of the power of melt mixing in the bath of a DC arc furnace under the action of electrovortex flows,” Journal of Sciences of Europe, Technical Science, Vol. 9, No. 9, pp. 111–115, 2016.

Search CrossRef
A. L. Kukharev, “Peculiarities of convective heat transfer in the melt of a multielectrode arc furnace,” (in Russian), Journal of Bulletin of ISPU, No. 2, pp. 13–22, 2020.

Publisher
Yu. Chernikhov, “Electromagnetic mixing of metal: a new step in the evolution of arc furnaces,” (in Russian), Journal of Science and Technology. Materials and Technologies, No. 4, pp. 10–13, 2019.

Search CrossRef
G. Paxey, “Device for electromagnetic stirring of metal.” https://metallurgist.pro/ustrojstvo-dlya-elektromagnitnogo-remeshivaniya-metalla, 2017.

Search CrossRef
Jan-Erik Eriksson et al., “Apparatus and method for electromagnetic stirring in an electrical arc furnace,” International Patent WO2012034586A1, 2012.

Search CrossRef
V. A. Sokolov, M. A. Gorbanenko, A. B. Lisafin, and M. D. Gasparyan, “The selection of melting unit for production of fused zirconia,” (in Russian), Journal of New Refractories, No. 12, pp. 3–9, Feb. 2021, https://doi.org/10.17073/1683-4518-2020-12-3-9

Publisher
Ye. A. Abdrakhmanov, “The state, problems and ways of development of electric arc technology of refractory materials in Kazakhstan,” (in Russian), Bulletin of the Almaty University of Energy and Communications, Vol. 3, No. 1, pp. 18–22, 2012.

Search CrossRef
“Rudnothermal electric furnaces.” Ore-thermal furnaces UkpNIIElektroterm. http://niiterm.com/ru/pechi-i-oborudovanie/dugovye-rudnotermicheskie-pechi-i-vspomogatelnoe-oborudovanie/rudnotermicheskie-pechi

Search CrossRef
V. A. Matvienko, Fundamentals of the Theory of Circuits: a Textbook for Universities. (in Russian), Ural Federal University named after the first President of Russia B.N. Yeltsin (Yekaterinburg), 2016.

Search CrossRef
Z. Wang, Y. Fu, N. Wang, and L. Feng, “3D numerical simulation of electrical arc furnaces for the MgO production,” Journal of Materials Processing Technology, Vol. 214, No. 11, pp. 2284–2291, Nov. 2014, https://doi.org/10.1016/j.jmatprotec.2014.04.033

Publisher
D. A. Vinogradov, I. O. Teplyakov, and V. B. Porokhonko, “Numerical simulation technique for electrovortex flows in melting units using CUDA technology,” (in Russian), in Topical Issues of Thermal Physics and Physical Fluid Dynamics, pp. 32–33, 2014.

Search CrossRef

Cited by

Criterial dependencies of the movement of the melt refractory material in the bath of an ore thermal furnace under electromagnetic influence

Yerkesh Abdrakhmanov | Anara Yegzekova | Zhansulu Ualieva

(2024)

About this article

Received

22 January 2023

Accepted

13 April 2023

Published

18 May 2023

SUBJECTS

Dynamics and oscillations in electrical and electronics engineering

DOI

https://doi.org/10.21595/vp.2023.23187

Keywords

ore-thermal furnace

electrovortex flow

electromagnetic mixing

electromagnetic force

Archimedes force

electromagnetic convection

thermal convection

field vorticity

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 01 25

Three-dimensional numerical simulation of multi-physical coupled environment during electromagnetic propulsion

Yuxin Yang, Peng Liu, Haojie Li, He Zhang

Research article

2020 10 19

Eddy current damper capable of collecting electric energy

Wenbin Yu, Guolai Yang

Research article

2019 09 30

Design study of a magnetoelectric-electromagnetic vibration energy converter for energy harvesting

Sonia Bradai, Slim Naifar, Olfa Kanoun

Research article

2018 02 15

Numerical simulation and optimization for electromagnetic noises of permanent magnet synchronous motors in vehicles

Gai Yan Bai

Y. Abdrakhmanov and G. Kalimbetov, “Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials,” Vibroengineering PROCEDIA, Vol. 49, pp. 147–152, May 2023, https://doi.org/10.21595/vp.2023.23187

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2023.23187
UR  - https://doi.org/10.21595/vp.2023.23187
TI  - Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials
T2  - Vibroengineering PROCEDIA
AU  - Abdrakhmanov, Yerkesh
AU  - Kalimbetov, Galym
PY  - 2023
DA  - 2023/05/18
PB  - JVE International Ltd.
SP  - 147-152
VL  - 49
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Abdrakhmanov_2023,
	doi = {10.21595/vp.2023.23187},
	url = {https://doi.org/10.21595/vp.2023.23187},
	year = 2023,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {49},
	pages = {147--152},
	author = {Yerkesh Abdrakhmanov and Galym Kalimbetov},
	title = {Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]Y. Abdrakhmanov and G. Kalimbetov, “Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials,” Vibroengineering PROCEDIA, vol. 49, pp. 147–152, May 2023, doi: 10.21595/vp.2023.23187.

Copy IEEE

Copied to clipboard!

Abdrakhmanov, Yerkesh, and Galym Kalimbetov. “Influence of an External Alternating Electromagnetic Field on Convective Flows in the Bath of an Ore-Thermal Furnace during the Melting of Oxide Refractory Materials.” Vibroengineering PROCEDIA 49 (May 18, 2023): 147–52. https://doi.org/10.21595/vp.2023.23187.

Copy Chicago

Copied to clipboard!

Influence of an external alternating electromagnetic field on convective flows in the bath of an ore-thermal furnace during the melting of oxide refractory materials

Abstract

Highlights

1. Introduction

2. Research methodology

3. Research results

4. Conclusions

References

Cited by

About this article

Related Articles