Non-linear analysis of eccentric compression of steel and steel fiber reinforced high strength concrete column

2.1. Steel fiber modeling

For the modeling of steel fibers, a secondary development in Python on ABAQUS was used to generate the fiber model shown in Fig. 1.

Fig. 1Schematic diagram of steel fiber model

2.2. Constitutive model of materials

The concrete compressive constitutive and peak compressive strains were calculated using the Yu Zhiwu, DING Faxing [5] method to obtain the stress-strain relationship equation:

where, $f_{cr}$ stand for the axial compressive stress in concrete; ${\epsilon }_{cr}$ refer to peak strain corresponding to peak compressive stress; $A_1$ is ratio of initial modulus of elasticity to peak cutline modulus of concrete; is descending section parameters.

In this paper, the stress-strain relationship equation of Ding Faxing, Yu Zhiwu calculation method [6] is used for the tensile constitutive structure and peak tensile strain of concrete:

where, $f_t$ stand for axial tensile strength; ${\epsilon }_{tr}$ is strain corresponding to peak tensile stress; $A$ and $\alpha$ is respectively the ascent and descent section parameters.

In this paper, Najar energy damage theory [7] is used to calculate the damage factor $D$, which is calculated as:

where, $D$, $E_0$ and $f\left(\epsilon \right)$ is respectively the damage factors, initial modulus of elasticity and stress-strain curve equation.

In this paper, we combine the characteristics of SSFRHSC biased columns and choose the failure criterion proposed by Zhenhai Guo et al. [8], which are given by:

where, $a$ is the limit value of ${\tau }_0$ when ${\sigma }_0$ approaches $-\infty$; $b$ stand for coordinate value of the intersection point between the meridian and the abscissa; $c$ refer to meridian parameters at different angles $\theta$; $d$ is coordinate value of the intersection point between tangent and abscissa.

The steel fiber and steel reinforcement adopt a double line model:

where, $E_1$ and $E_2$ is respectively initial elastic modulus and post yield elastic modulus of steel.

This article uses Eq. (6) and (7) to convert experimental data. Calculate the plastic strain value using Eq. (8):

where, ${\sigma }_{com}$ and ${\epsilon }_{com}$ stands for nominal stress and nominal strain; ${\epsilon }^{pl}$, ${\epsilon }^t$ and ${\epsilon }^{el}$ is respectively true plasticity, overall and true elastic strain values.

2.3. Model meshing and interaction

C3D8R solid units are used for steel and concrete components; the steel bars and steel fiber components use T3D2 truss units.

This article selects a grid side length of 0.02 m for concrete columns, 0.025 m for steel profiles, 0.048 m for steel reinforcement cages, and 0.035 m for steel fibers. The finite element model mesh division diagram of each element component of the composite column is shown in Fig. 2.

Considering the contact relationship between the steel section and the concrete interface in the real situation, the volume part of the steel section is deducted from the inside of the concrete when modelling the concrete, and then the contact between the outer surface of the steel section and the interface of the concrete is set, where the Specify tolerance for adjustment zone is set to 0.0001, and Normal Behavior is set to Hard Contact, define the friction with penalty function, the coefficient is set to 0.5, after calculation and comparison, this way is more accurate than directly embedding the steel section in concrete. The Embedding region is used for the action relationship of steel cage, steel fiber and concrete column respectively.

Fig. 2Grid partition diagram of each component of combined column

a) Concrete

b) Steel fiber

c) Rebar cage

d) Section steel

3.1. Finite element model validation

Fig. 3 is a comparison of the load-displacement curves obtained by simulating the six specimens used in the literature [4]. As can be seen from Fig. 1, the load-displacement curves of the test specimens and the simulated specimens are in good agreement, and the peak load difference is within 10 %, which indicates that the simulation effect and the test are in good agreement.

Fig. 3Comparison of calculated load-displacement curve and test curve of section steel fiber high-strength concrete column

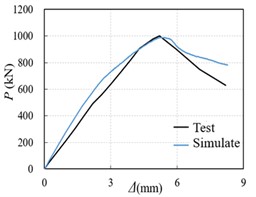
a) SSFRHSC-1 test-piece

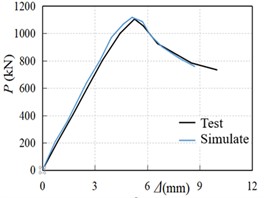
b) SSFRHSC-2 test-piece

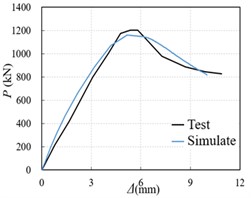
c) SSFRHSC-3 test-piece

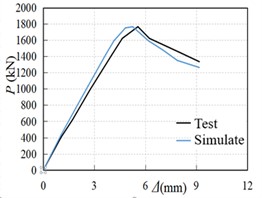
d) SSFRHSC-4 test-piece

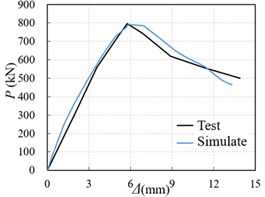
e) SSFRHSC-5 test-piece

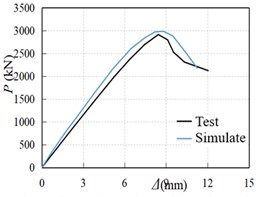
f) SSFRHSC-6 test-piece

3.2. Finite element expansion analysis

In order to more comprehensively study the mechanical properties of steel fiber reinforced high-strength concrete columns under eccentric compression, and better guide the related design of such members, based on the correctness of the model, the model expansion analysis was carried out on the influence parameters such as steel fiber volume ratio, concrete strength, eccentricity, slenderness ratio, and other parameters of the specimen remained unchanged. See Table 1 for dimensions of simulated components.

Fig. 4 shows the simulation results of five specimens with different steel fiber volume rates. It can be seen from Fig. 4 that the ultimate bearing capacity of the specimens increases by 10.11 %, 9.27 %, 6.48 %, 6.09 % and 3.53 % for each 0.5 % increase in fiber rate from 0.5 % to 3 %, and that steel fibers improve the ductility of the specimens.

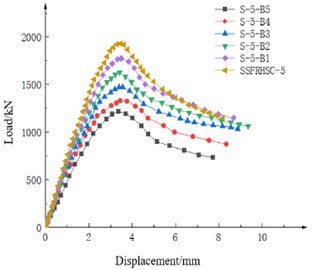
Fig. 5 shows the simulation results for five different concrete strength specimens. It can be seen from Fig. 5 that the peak loads of the specimens increased by 9.39 %, 10.73 %, 10.46 %, 9.12 % and 8.68 % for each increase in concrete strength from C40 to C90, respectively.

Fig. 4Load-displacement curves of specimens with different steel fiber volume ratios

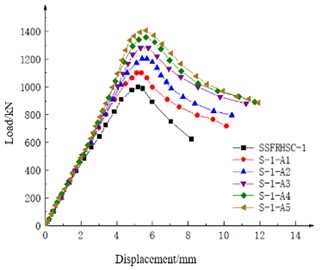
Fig. 5Load-displacement of concrete specimens with different strength

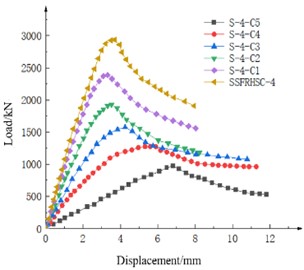
As shown in Fig. 6, the load displacement curves of six simulated specimens with different eccentricities can be seen from the figure: the specimens with eccentricities of 0 mm, 20 mm and 40 mm are brittle failure, and the bearing capacity decreases rapidly after the column reaches the peak load. The specimens with eccentricity of 60 mm, 80 mm and 100 mm are ductile failure. When the column reaches the peak load, the falling section is relatively gentle. It can be seen from Fig. 6 that with the eccentricity from 0 to 100 mm, the peak load of the test piece decreases by 18.66%, 19.35 %, 18.23 %, 18.99 % and 21.52 % for each 20 mm increase.

Fig. 6Influence of RC column damage degree on load-displacement curve of specimen